DOCSLIB.ORG

Statistical Based Regional Flood Frequency Estimation Study For

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistical Based Regional Flood Frequency Estimation Study For Statistical Based Regional Flood Frequency Estimation Study for South Africa Using Systematic, Historical and Palaeoflood Data Pilot Study – Catchment Management Area 15 by D van Bladeren, P K Zawada and D Mahlangu SRK Consulting & Council for Geoscience Report to the Water Research Commission on the project “Statistical Based Regional Flood Frequency Estimation Study for South Africa using Systematic, Historical and Palaeoflood Data” WRC Report No 1260/1/07 ISBN 078-1-77005-537-7 March 2007 DISCLAIMER This report has been reviewed by the Water Research Commission (WRC) and approved for publication. Approval does not signify that the contents necessarily reflect the views and policies of the WRC, nor does mention of trade names or commercial products constitute endorsement or recommendation for use EXECUTIVE SUMMARY INTRODUCTION During the past 10 years South Africa has experienced several devastating flood events that highlighted the need for more accurate and reasonable flood estimation. The most notable events were those of 1995/96 in KwaZulu-Natal and north eastern areas, the November 1996 floods in the Southern Cape Region, the floods of February to March 2000 in the Limpopo, Mpumalanga and Eastern Cape provinces and the recent floods in March 2003 in Montagu in the Western Cape. These events emphasized the need for a standard approach to estimate flood probabilities before developments are initiated or existing developments evaluated for flood hazards. The flood peak magnitudes and probabilities of occurrence or return period required for flood lines are often overlooked, ignored or dealt with in a casual way with devastating effects. The National Disaster and new Water Act and the rapid rate at which developments are being planned will require the near mass production of flood peak probabilities across the country that should be consistent, realistic and reliable. At present the methodologies for flood frequency analysis in South Africa consists of three basic approaches, all of which have certain validity limits (Kovacs, 1993): Deterministic methods (Rational, Synthetic unit hydrograph, Direct runoff hydrograph, SCS, etc.) Statistical methods such as the LP3, GEV and Log-normal (annual maximum flood series data) Empirical methods (Midgley-Pitman, HRU 1/71, CAPA and RMF) Experience in the Department of Water Affairs and Forestry (DWAF) has shown that these methods often give vastly different results and unless a certain amount of judgement and experience can be used, the selection of final values may be inconsistent and subjective. This pilot study provides a basis to develop simple and consistent methodologies for the rest of the country to estimate flood peaks and their associated probabilities for use by authorities, consultants and planners. Since the last extensive review of the methodologies in 1970’s to early 1980’s the following should be noted that justify a review of the methodologies: The period of observation has been extended by a further 25 to 30 years i.e. more data, The number of sites are significantly more, South Africa has had several extreme flood events that added to the extreme flood peak data base, The technology regarding the statistical analysis of flood data has improved, The gathering of historical data by DWAF (van Bladeren, 1992) has in many areas increased the period of observation to between 100 to 150 years, and i By including the modelling and dating of palaeofloods, where possible, this period may be extended to more than 200 years, which is the upper limit of the normally requested design flood peaks used in design and planning. From the above it was clear that the revision and updating of the methods was long overdue and this project could be seen as one way to resuscitate the neglected field of flood research in South Africa. The inclusion of palaeofloods is based on the success of previous projects completed for the WRC by the Council for Geo-Science and DWAF. That project demonstrated the value that the inclusion of palaeoflood data in flood frequency studies (Zawada et al., 1996). This project integrates systematic, historical and palaeoflood data to provide flood growth curves that are scaled using an index flood to provide estimates of flood peaks and their associated probabilities. The development is motivated by the stated desire of the Committee of State Road Authorities in their guidelines for the hydraulic design and maintenance of river crossings (TRH 25, 1994) and Alexander (1990) who identified the lack of regional growth curves for southern Africa as a serious drawback when selecting applicable flood probabilities. This report of the pilot study is an attempt to develop a robust and reliable method of estimating the full range of usually requested flood peaks used in design, based on index floods and regional growth curves that are obtained from the analysis of observed data. The project integrates systematic, historical and palaeoflood data to derive growth curves for floods and using selected catchment characteristics to develop an index flood estimation methodology. The pilot area selected for the study was Catchment Management Area (CMA) 15 in the Eastern Cape. CMA 15 includes drainage regions K7-9, L, M, N, P and Q. Drainage regions J, K3-6, R and S were also included to provide fringe information. REVIEW OF FLOOD AND REGIONAL FLOOD HYDROLOGY IN SOUTH AFRICA Flood hydrology in South Africa (Kovacs, 1993) is generally classified as deterministic, statistical or empirical. Several regional flood studies have been undertaken in South Africa using systematic data. Most of the previous regional studies in South Africa defined regions based on climate or drainage regions. Data used to develop the methods for the previous studies only used gauged records and are thus based on relatively short periods of observation. The only study that included historical data is the recently developed SDF (Alexander, 2002) and the previous attempt by van Bladeren (1993). From the review, the Catchment Parameter (CAPA) method developed by McPherson (1983) to estimate the mean annual flood was selected as the basis to estimate the index flood for this study. The CAPA method uses several catchment variables to estimate a lumped parameter and is site specific. Alexander (2002) and van Bladeren (1993) have evaluated several distributions in various studies throughout South Africa and ii have concluded that the log-Pearson type III distribution is the most appropriate for South Africa. Another contender is the general extreme value distribution. REGIONAL FLOOD STUDY CMA 15 The regional flood study for CMA 15 consisted of the gathering of annual maximum flood (AMF) peak data, determination and estimation of relevant catchment characteristics, the development of a methodology to estimate the index flood (Qi), the development of flood peak growth curves and the comparison or verification of the results obtained using the proposed methodology against those obtained, using other methods and actual observed flood data. The 348 sites identified on the Hydrological Information System (HIS) of DWAF for the study area was reduced to 112 useable sites after assessment of the sites. All the sites originally identified are shown in Appendix A and the sites finally used and their AMF, historical and palaeoflood data are listed in Appendix B. A break-down of the data used is summarised in the table below. Summary of Flood Peak Data Sets (Appendix B) Drainage Period of Observation (years) Region Systematic Data Including Historical Data Including Palaeoflood Data Sites Average Maximum Sites Average Maximum Sites Average Maximum J 26 46 90 5 109 152 2 2996 3000 K 15 39 42 - - - - - - L 11 55 83 4 100 154 1 1901 1901 M 3 49 76 1 148 148 - - - N 5 69 97 2 130 135 2 7996 8001 P 3 37 45 2 111 113 - - - Q 20 63 96 6 141 182 - - - R 17 61 79 6 141 154 - - - S 12 40 54 1 127 127 - - - Average - 51 - - 125 - - 4777 - Total 112 5766 - 27 3394 - 5 23885 - The average period of observation for the systematic data is 51 years. With inclusion of the historical data the period of observation is 125 years and when the palaeoflood data is included, the period of observation is extended to 4777 years. The applicability of the combined data sets may thus be taken as 10000 years (twice the period of observation). The development of the index flood used catchment characteristics generated by a GIS database using the WR90 data and topographical data derived from the 1:50000 mapping series supplied by DWAF. The index flood development used the same methodology as the CAPA method (McPherson, 1983) but during the iii analysis it was found that some of the variables used to calculate the lumped parameter M, used in the CAPA method, should be replaced and this resulted in a new lumped parameter M’ being proposed. This new methodology is presently referred to as NCAPA and the parameter M’ and is defined as; Where; A=Catchment Area (km2) MAP=Mean Annual Precipitation (mm) s=Standard River Slope – 1085 (m/m) and L=Longest Stream Length (km) The land-use or catchment characteristics defined by soils, geology, vegetation and MAP is taken into account by a regionalisation that is based on previous studies, MAP and vegetation. This regionalisation resulted in regional boundaries that are very similar to those shown for the veld types as shown in the HRU 1/72 report. The HRU 1/72 veld type zones were thus used for the classification of the regions identified in the study and is shown below. iv The base used for the derivation of the index flood is the mean annual flood obtained from the analysis of the log transformed data and is referred to as the log derived mean annual flood (Qml) in the report. The Qml proved to be the most robust parameter and is least affected by period of observation and outliers than either the mean annual or median annual flood estimates.
Load more

Recommended publications
  • 2018/19 Final Reviewed
    0 0 A STORY OF EDEN DISTRICT MUNICIPALITY A place of opportunities whose sole focus is serving its community. Municipality well located on the N2 between two (2) of the countries cities. A district with good transport and road infrastructure network. Situated halfway between national ports and has its own two (2) recreational ports. Pristine beaches and a relatively unspoilt environment. The district is well known for its tourist’s attractions and natural beauty 1 Growth Nodes in Eden District Area The economic growth and development of the district depends on monopolising on its competitive advantages. The district has a wide range of competitive advantages ranging from: - The coastal line, with opportunities of ocean economy, coastal tourism. - Large Forestry, - Arable land for agriculture and farming, - Effective natural resources. WC:044 This municipality is situated in a district, which is informally known as the Garden Route, with its hubs, nestled among the slopes of the majestic Outeniqua Mountains and flanked by the Indian Ocean to the south. It is situated on the major transport routes between Cape Town in the south and Port Elizabeth in the east. WC:041 Kannaland municipality is renowned for its cheese factories and the production of world famous dairy and wine products. WC:043 Its main economic activity is agriculture (Aloes, cattle, dairy, ostriches, sheep, timber, vegetable and wines), fishing light industry, petrochemicals and tourism. WC:047 This municipality is situated along the Garden Route. Plettenberg bay is rife with a number of invertebrates such as anemones, nudibranchs and sponges. Bitou has over four different kinds of reefs and is particularly famous for being the best night-time diving spot.
    [Show full text]
  • Gamtoos Estuary Management Plan Volume I Situation Assessment
    Enviro-Fish Africa (Pty) Ltd. C.A.P.E. ESTUARIES MANAGEMENT PROGRAMME GAMTOOS ESTUARY MANAGEMENT PLAN VOLUME I SITUATION ASSESSMENT (STATE OF PLAY REPORT) Produced by: Enviro-Fish Africa (Pty) Ltd. P.O. Box 94 Grahamstown 6140 Produced for: Cape Nature December 2007 C.A.P.E. Estuaries Management Programme; Gamtoos Estuary Management Plan: Situation Assessment 1 Enviro-Fish Africa (Pty) Ltd. 1. INTRODUCTION Estuarine ecosystems are not isolated systems. They form an interface between marine and freshwater systems and are part of regional, national and global ecosystems either directly via water flows or indirectly through the movement of fauna. In addition to the biota that these estuaries support, they provide a range of goods and services (uses) to the inhabitants of the various regions. Disturbances in one estuary can influence a wide variety of habitats and organisms in the broader freshwater or marine ecosystem. Thus, the interaction between the systems and users creates a delicate balance, the sustainability of which needs to be addressed by some form of management plan. In order to address this balance in a consistent manner in the Cape Floristic Region (CFR), the Cape Action for People and the Environment (C.A.P.E.) Estuaries Management Programme has developed a holistic and inclusive management process representative of all stakeholders. The programme is governed by a Task Team comprising of officials from C.A.P.E., CapeNature, Marine and Coastal Management (MCM), the Department of Water Affairs and Forestry (DWAF), the Eastern Cape Parks Board (ECPB) and the Council for Scientific and Industrial Research (CSIR), which heads the technical support group.
    [Show full text]
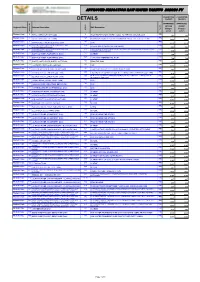
  • Details Charges Charges
    APPROVED IRRIGATION RAW WATER TARIFFS 2020/21 FY CONSUMPTIVE CONSUMPTIVE DETAILS CHARGES CHARGES APPROVED APPROVED 2019/20 2020/21 Regional Office Scheme Description SMP Description Charges Charges Sector SMP SMP ID Scheme IDScheme (c/m³) (c/m³) Western Cape 6 4 IRR BERG RIVER (VOELVLEI DAM) FROM TWENTY-FOUR RIVERS CANAL TO THE IRRIGATION BOARD 1,52 1,52 Western Cape 6 127 IRR BERG RIVER (VOELVLEI DAM) IRRIGATION FROM BERG RIVER DOWNSTREAM OF THE VOELVLEI DAM 13,22 13,22 Western Cape 9 48 IRR BRAND RIVER (MIERTJIESKRAAL DAM) DAM 11,75 11,75 10 BREEDE RIVER (GREATER BRANDVLEI AND 116 IRR Western Cape BREEDE RIVER CONSERVATION BOARD KWAGGASKLOOF DAMS) 3,46 3,46 Western Cape 10 BREEDE RIVER (GREATER BRANDVLEI AND 417 PURCHASED WATER RIGHTS & OTHER BOARDS (EXCLUDING BREEDE RIVER IRR KWAGGASKLOOF DAMS) CONSERVATION BOARD) 6,24 6,33 Western Cape 12 51 IRR BUFFALO RIVER (FLORISKRAAL-DAM) SCHEME 7,44 7,64 Western Cape 12 420 IRR BUFFALO RIVER (FLORISKRAAL-DAM) C VAN WYK PREFERENTIAL RIGHT 7,44 7,64 Western Cape 13 52 IRR BUFFELJAGTS RIVER (BUFFELJAGTS DAM) FROM THE DAM 7,37 7,60 Western Cape 17 55 IRR CORDIERS RIVER (OUKLOOF DAM) DAM 11,12 11,12 Western Cape 25 62 IRR DUIVENHOKS RIVER (DUIVENHOKS DAM) FROM DUIVENHOKS RIVER (DUIVENHOKS DAM) 7,51 7,72 Western Cape 26 605 IRR ELANDS RIVER (ELANDS-KLOOF DAM) EXISTING DEVELOPMENT FROM THE ELANDS RIVER (ELANDS-KLOOF DAM) 0,76 0,88 26 606 NEW DEVELOPMENT (DAM COSTS INCLUDED) FROM THE ELANDS RIVER IRR Western Cape ELANDS RIVER (ELANDS-KLOOF DAM) (ELANDS-KLOOF DAM) 9,05 9,29 Western Cape 31 68 IRR GAMKA
    [Show full text]
  • Moving People and Goods in the Gamtoos Valley: a Revealing Case Study
    MOVING PEOPLE AND GOODS IN THE GAMTOOS VALLEY: A REVEALING CASE STUDY van der Mescht, J. Department of Civil Engineering, Port Elizabeth Technikon, Private Bag X6011, Port Elizabeth, 6000 South Africa. Tel: +2741 5043550. Fax: +2741 5043491. E-mail: [email protected] ABSTRACT Primary transportation infrastructure in the Gamtoos Valley, a fertile agricultural district located to the west of Port Elizabeth, consists of a single-lane surfaced road namely Route 331, as well as a narrow gauge railway line. While the road pavement is in a poor condition due to lack of maintenance and extensive damage caused by an increasing number of heavy vehicles, the rail service is under-utilised and its future uncertain. The railway is used exclusively for the conveyance of export fruit via the Port Elizabeth harbour and is only operational for the duration of the citrus season that lasts from the beginning of April till the end of October. This paper reports on a preliminary investigation into the possibility of shifting passengers and freight from road to rail in order to relieve the pressure on the road system, to optimise the use of existing transportation facilities and to preserve and extend the working life of valuable road and rail assets. The logistics of hauling both imported and exported goods were analysed to establish what portion thereof could probably be moved by rail instead of by road. Other issues that were looked at included the offering of rail concessions to private companies, the introduction of a passenger service between Loerie and Patensie and the impact that current policies of the national rail operator, Spoornet, have on the provision of a satisfactory service to existing and potential rail clients.
    [Show full text]
  • Freshwater Fishes
    WESTERN CAPE PROVINCE state oF BIODIVERSITY 2007 TABLE OF CONTENTS Chapter 1 Introduction 2 Chapter 2 Methods 17 Chapter 3 Freshwater fishes 18 Chapter 4 Amphibians 36 Chapter 5 Reptiles 55 Chapter 6 Mammals 75 Chapter 7 Avifauna 89 Chapter 8 Flora & Vegetation 112 Chapter 9 Land and Protected Areas 139 Chapter 10 Status of River Health 159 Cover page photographs by Andrew Turner (CapeNature), Roger Bills (SAIAB) & Wicus Leeuwner. ISBN 978-0-620-39289-1 SCIENTIFIC SERVICES 2 Western Cape Province State of Biodiversity 2007 CHAPTER 1 INTRODUCTION Andrew Turner [email protected] 1 “We live at a historic moment, a time in which the world’s biological diversity is being rapidly destroyed. The present geological period has more species than any other, yet the current rate of extinction of species is greater now than at any time in the past. Ecosystems and communities are being degraded and destroyed, and species are being driven to extinction. The species that persist are losing genetic variation as the number of individuals in populations shrinks, unique populations and subspecies are destroyed, and remaining populations become increasingly isolated from one another. The cause of this loss of biological diversity at all levels is the range of human activity that alters and destroys natural habitats to suit human needs.” (Primack, 2002). CapeNature launched its State of Biodiversity Programme (SoBP) to assess and monitor the state of biodiversity in the Western Cape in 1999. This programme delivered its first report in 2002 and these reports are updated every five years. The current report (2007) reports on the changes to the state of vertebrate biodiversity and land under conservation usage.
    [Show full text]
  • A Classification of the Subtropical Transitional Thicket in the Eastern Cape, Based on Syntaxonomic and Structural Attributes
    S. Afr. J. Bot., 1987, 53(5): 329 - 340 329 A classification of the subtropical transitional thicket in the eastern Cape, based on syntaxonomic and structural attributes D.A. Everard Department of Plant Sciences, Rhodes University, Grahamstown, 6140 Republic of South Africa Accepted 11 June 1987 Subtropical transitional thicket, traditionally known as valley bushveld, covers a significant proportion of the eastern Cape. This paper attempts to classify the subtropical transitional thicket into syntaxonomic and structural units and relate it to other thicket types on a continental basis. Twelve sites along a rainfall gradient were sampled for floristic and structural attributes. The floristic data were classified using TWINSPAN. Results indicate that the class subtropical transitional thicket has at least two orders of vegetation, namely kaffrarian thicket and kaffrarian succulent thicket. Two forms of thicket were recognized for both these orders viz. mesic kaffrarian thicket and xeric kaffrarian thicket for the kaffrarian thicket and mesic succulent thicket and xeric succulent thicket for the kaffrarian succulent thicket. Ordination of site data by DECORANA grouped sites according to these vegetation categories and in a sequence along axis 1 to which the rainfall gradient can be clearly related. Variation within the mesic kaffrarian thicket was however greater than between some of the other thicket types, indicating that more data are required before these forms of thicket can be formalized. Composition, endemism, diversity and the environmental controls on the distribution of the thicket types are discussed. 'n Aansienlike gedeelte van die Oos-Kaap word beslaan deur subtropiese oorgangsruigte, wat tradisioneel as valleibosveld bekend is. Hierdie studie is 'n poging om subtropiese oorgangsruigte in sintaksonomiese en strukturele eenhede te klassifiseer en dit op 'n kontinentale basis in verband met ander ruigtetipes te bring.
    [Show full text]
  • The Valuation of Changes to Estuary Services in South Africa As a Result of Changes to Freshwater Inflow
    THE VALUATION OF CHANGES TO ESTUARY SERVICES IN SOUTH AFRICA AS A RESULT OF CHANGES TO FRESHWATER INFLOW BY SG HOSKING, TH WOOLDRIDGE, G D1MOPOULOS, M MLANGENI, C-H LIN, M SALE AND M DU PREEZ DEPARTMENT OF ECONOMICS AND ECONOMIC HISTORY AND DEPARTMENT OF ZOOLOGY/ UNIVERSITY OF PORT ELIZABETH REPORT TO THE WATER RESEARCH COMMISSION WRC REPORT NO: 1304/1/04 ISBN NO: 1-77005-278-X DECEMBER 2004 II DISCLAIMER This report emanates from a project financed by the Water Research Commission (WRC) and is approved for publication. Approval does not signify that the contents necessarily reflect the views and policies of the WRC or the members of the project steering committee, nor does mention of trade names or commercial products constitute endorsement or recommendation for use. Ill ACKNOWLEDGEMENTS The research in this report emanated from a project funded by the Water Research Commission and entitled: "THE VALUATION OF CHANGES TO ESTUARY SERVICES IN SOUTH AFRICA AS A RESULT OF CHANGES TO FRESHWATER INFLOW" The authors contributed in the following sections: T Wooidridge - Chapters One and Five G Dimopoulos - Chapters One, Three, Five and Six C-H Lin - Chapters Four and Seven M Sale - Chapters Two, Five and Six S Hosking - all Chapters M du Preez assisted S Hosking with the editorial work M Mlangeni - Chapters Five and Six. The Steering Committee responsible for this project consisted of the following persons: Dr GR Backeberg Water Research Commission (Chairman) Dr SA Mitchell Water Research Commission Dr J Turpie University of Cape Town Mr A Leiman University of Cape Town Prof MF Viljoen University of the Free State Dr J Adams University of Port Elizabeth Dr M du Preez University of Port Elizabeth The funding of the project by the Water Research Commission and the contribution of the members of the Steering Committee is gratefully acknowledged.
    [Show full text]
  • Water for Food and Ecosystems in the Baviaanskloof Mega Reserve Land and Water Resources Assessment in the Baviaanskloof, Easter
    Water for Food and Ecosystems in the Baviaanskloof Mega Reserve Land and water resources assessment in the Baviaanskloof, Eastern Cape Province, South Africa H.C. Jansen Alterra-report 1812 Alterra, Wageningen, 2008 ABSTRACT Jansen, H.C., 2008. Walerfor bood and hicosystems in the baviaanskloofMega Reserve. IMnd and water resources assessment in the Baviaanskloof,Hastern Cape Province, South Africa. Wageningen, Alterra, Alterra-report 1812. 80 pages; 21 figs.; 6 tables.; 18 refs. This report describes the results of the land and water assessment for the project 'Water for Food and Ecosystems in the Baviaanskloof Mega Reserve'. Aim of the project is to conserve the biodiversity in a more sustainable way, by optimizing water for ecosystems, agricultural and domestic use, in a sense that its also improving rural livelihoods in the Baviaanskloof. In this report an assessment of the land and water system is presented, which forms a basis for the development and implementation of land and water policies and measures. Keywords: competing claims, IWRM, land management, nature conservation, policy support, water management, water retention ISSN 1566-7197 The pdf file is tree of charge and can he downloaded vi«i the website www.ahctra.wur.nl (go lo Alterra reports). Alterra docs not deliver printed versions ol the Altena reports. Punted versions can be ordered via the external distributor. I-or oidcrmg have a look at www.li tx> ni l) ljtl.nl/mppcirtc ilser vice . © 2008 Alterra P.O. Box 47; 6700 AA Wageningen; The Netherlands Phone: + 31 317 484700; fax: +31 317 419000; e-mail: info.alterra@,wur.nl No part of this publication may be reproduced or published in any form or by any means, or stored in a database or retrieval system without the written permission of Alterra.
    [Show full text]
  • Amathole District Municipality WETLAND REPORT | 2017
    AMATHOLE DISTRICT MUNICIPALITY WETLAND REPORT | 2017 LOCAL ACTION FOR BIODIVERSITY (LAB): WETLANDS SOUTH AFRICA Biodiversity for Life South African National Biodiversity Institute Full Program Title: Local Action for Biodiversity: Wetland Management in a Changing Climate Sponsoring USAID Office: USAID/Southern Africa Cooperative Agreement Number: AID-674-A-14-00014 Contractor: ICLEI – Local Governments for Sustainability – Africa Secretariat Date of Publication: June 2017 DISCLAIMER: The author’s views expressed in this publication do not necessarily reflect the views of the United States Agency for International Development or the United States Government. FOREWORD Amathole District Municipality is situated within the Amathole District Municipality is also prone to climate central part of the Eastern Cape Province, which lies change and disaster risk such as wild fires, drought in the southeast of South Africa and borders the and floods. Wetland systems however can be viewed Indian Ocean. Amathole District Municipality has as risk reduction ecological infrastructure. Wetlands a land area of 21 595 km² with approximately 200 also form part of the Amathole Mountain Biosphere km of coastline stretching along the Sunshine Coast Reserve, which is viewed as a conservation and from the Fish River to just south of Hole in the Wall sustainable development flagship initiative. along the Wild Coast. Amathole District Municipality coastline spans two bio-geographical regions, namely Amathole District Municipality Integrated the warm temperate south coast and the sub-tropical Development Plan (IDP) recognises the importance east coast. of wetlands within the critical biodiversity areas of the Spatial Development Framework (SDF). Amathole District Municipality is generally in a good Sustainable development principles are an natural state; 83.3% of land comprises of natural integral part of Amathole District Municipality’s areas, whilst only 16.7% are areas where no natural developmental approach as they are captured in the habitat remains.
    [Show full text]
  • Biomonitoring of the Keiskamma River System (R10 Catchment)
    BIOMONOTORING OF THE KIESKAMMA RIVER SYSTEM (R 10 CATCHMENT) Figure 1; Sandile Dam March 2008 PREPARED BY: Mlondolozi N. Mbikwana Assisted by: Tembela Bushula Collection of data: M.N. Mbikwana, K. Mkosana, E. Weni, T Bushula and N. Finca PO BOX 7019 EAST LONDON 5201 EXECUTIVE SUMMARY The main objective of the South African National River Health Programme (NRHP) makes use of the instream and riparian biological communities like the fish, macro invertebrates and vegetation to assess the ecological health or condition of rivers. These biological communities are always found in rivers and they are often affected by any disturbance that occurs in the river ecosystem. This report provides the results of the biomonitoring survey that was undertaken in November 2007. Field indices used for data collection included the South African Scoring System version 5.0 (SASS5) for Macro invertebrates and the Fish Assemblage Integrity Index for fish (FAII). Ten biomonitoring sites were selected in the Keiskamma River system; this includes three sites in the Tyume River (a tributary to Keiskamma River) and they are: Site Description Coordinates Site Code 1 Tyume Head waters (Hogsback) S32o 36’ 39.8”, E26o R1Tyum-Hogsb 56’ 52.2” 1a ** Tyume Head waters (Sompondo S32o 37’ 34.2”, E26o R1Tyum-Sompo ** Village) 57’ 19.9” 2 Tyume Fort Hare S32o 46’ 44.6”, E26o R1Tyum-Forth 51’ 21.5” 3 Tyume before confluence with S32o 54’ 06.2”, E26o R1Tyum-Becon Keiskamma river 55’ 40.0” 4 Keiskamma above confluence with S32o 54’ 41.9”, E26o R1Keis-abcon Tyume 56’ 17.6” 5 Keiskamma
    [Show full text]
  • National Environmental Management: Protected Areas Act: Amendment Of
    STAATSKOERANT, 27 MAART 2013 No. 36295 3 GOVERNMENT NOTICE DEPARTMENT OF ENVIRONMENTAL AFFAIRS No. 236 27 March 2013 NATIONAL ENVIRONMENTAL MANAGEMENT: PROTECTED AREAS ACT, 2003 (ACT NO. 57 OF 2003) AMENDMENT OF SCHEDULE 2 TO THE NATIONAL ENVIRONMENTAL MANAGEMENT: PROTECTED AREAS ACT, 2003 (ACT NO. 57 OF 2003) I, Bomo Edith Edna Molewa, Minister of Water and Environmental Affairs, in terms of section 20(6)(b) of the National Environmental Management: Protected Areas Act, 2003 (Act No. 57 of 2003), hereby amend Schedule 2 to the National Environmental Management: Protected Areas Act, 2003 (Act No. 57 of 2003) in the Schedule hereto. BOM ED IA MOLEWA MINISTER OF WATER AND ENVIRONMENTAL AFFAIRS 4 No. 36295 GOVERNMENT GAZETTE, 27 MARCH 2013 SCHEDULE In terms of section 20(6)(a) of the Act, each area defined shall be a national park under the name assigned to it in the Schedule. In terms of section 47(1) of the Act, the air space to a level of 2 500 feet above the highest point of the park (included in the Schedule) is included in the national park. [Schedule 2 amended by Proc. 294/78, s. 2 of Act 60/79, Proc. 201/79, Proc. 44/82, Proc.125/83, Proc. 132/83, Proc. 8/84, Proc. 210/84, Proc. 35/85, Proc. 138/85, GN 1933/86, GN 1934/86, GN 5/87, GN 1385/87, GN 1753/87, GN 2509/87, GN 2814/87, GN 2856/87, GN 225/88, GN 1047/88, GN 1249/88, GN 1490/88, GN 577/89, GN 703/89, GN 1374/89, GN 395/91, GN 1211/91, GN 2159/92, GN 214/93, GN 1766/93, GN 2201/93, GN 2202/93, GN 37/94, GN 183/94, GN 248/94, GN 857/94, GN 1227/94, GN 1228/94, GN 1705/94, GN 1947/94 , GN 2244/94, GN 1582/95, GN 1732/95, GN 537/96, GN 538/96, GN R599/96, GN 1077/96, GN 1138/96, GN 1139/96, GN 1140/96, s.
    [Show full text]
  • L-Mnr:~ Cape Province 2765 MAIN STREET Dept
    Uncertain Future for Southern Race ofCape Parrot Marsh Farms by Andre' Boshoff INCUBATORS Republic ofSouth Africa There are considered to be nine 28.3 mm), and the latter has a lighter, • FEATURING fully automatic species in the genus Poicepbalus more greyish head. turners. Adjustable temperature The type locality of P. r. and humidity control. which has been divided into two robustus, groups, namely the P. robustus; the nominate race, is given as "east­ superspecies with two species and ern Cape" (Cape Province, South the P. meyeri superspecies with seven Africa); P.r. robustus is endemic to species. The two P. robustus species, South Africa (see Figure 1). For the namely P. robustus and P. gulielmi, sake of convenience the Ciskei and are similar in size and plumage char­ Transkei, two small independent acteristics. P. robustus can be divided homelands which were formerly part TURN-X into three isolated populations which of the eastern Cape Province (referred Up to 72 eggs. differ at the subspecific level; the to hereafter as "E. Cape") are head is brownish in the most included as part of the E. Cape in Fig­ southerly form, P.r. robustus, which ure 1. is restricted to the southern part of P. r. robustus is listed as Vulnerable Africa, and silvery grey in the remain­ in the South African Red Data Book ing two forms, P.r. juscicollis in west - Birds and if it proves to be a sepa­ Africa and P.r. suabelicus in south­ rate species then steps to ensure its central Africa. The plumage colour survival will require urgent attention.
    [Show full text]