DOCSLIB.ORG

Autocorrelation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Autocorrelation When a regression model is fitted to time series data, the residuals often violate the standard assumptions by being correlated. Because one residual is correlated with another in the same series, we refer to auto-correlation. Notation, emphasizing the autocorrelated nature of the residuals: Yt = E(Yt jxt ) + Rt = β0 + β1xt;1 + β2xt;2 + ··· + βk xt;k + Rt : 1 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II The correlation of Rt with Rt−1 is called a lagged correlation, specifically the lag 1 correlation. More generally, the correlation of Rt with Rt−m is the lag m correlation, m > 0. Autocorrelation is usually strongest for small lags and decays to zero for large lags. Autocorrelation depends on the lag m, but often does not depend on t. 2 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II When the correlation of Rt with Rt−m does not depend on t, and in addition: the expected value E(Rt ) is constant; the variance var(Rt ) is constant; the residuals are said to be stationary. Regression residuals have zero expected value, hence constant expected value, if the model is correctly specified. They also have constant variance, perhaps after the data have been transformed appropriately, or if weighted least squares has been used. 3 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Correlogram The graph of corr(Rt ; Rt−m) against lag m is the correlogram, or auto-correlation function (ACF). For the SALES35 example: sales <- read.table("Text/Exercises&Examples/SALES35.txt", header = TRUE) l <- lm(SALES ~ T, sales) acf(residuals(l)) The ACF is usually plotted including the lag 0 correlation, which is of course exactly 1. The blue lines indicate significance at α = :05. 4 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Modeling Autocorrelation Sometimes the ACF appears to decay exponentially: ACF(m) ≈ φm; m ≥ 0; −1 < φ < 1: The 1st order autoregressive model, AR(1), has this property; if Rt = φRt−1 + t ; where t has constant variance and is uncorrelated with t−m for all m > 0, then m corr(Rt ; Rt−m) = φ ; m > 0: 5 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II General autoregressive model, AR(p): Rt = φ1Rt−1 + φ2Rt−2 + ··· + φpRt−p + t : ACF decays exponentially, but not exactly as φm for any φ. Moving average models, MA(q): Rt = t + θ1t−1 + θ2t−2 + ··· + θqt−q: ACF is zero for lag m > q. 6 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Combined ARMA(p; q) model: Rt = φ1Rt−1 + φ2Rt−2 + ··· + φpRt−p + t + θ1t−1 + θ2t−2 + ··· + θqt−q: ACF again decays exponentially, but not exactly as φm for any φ. 7 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Regression with Autocorrelated Errors To fit the regression model Yt = E(Yt jxt ) + Rt we must specify both the regression part E(Yt jxt ) = β0 + β1xt;1 + β2xt;2 + ··· + βk xt;k and a model for the autocorrelation of Rt , say ARMA(p; q) for specified p and q. Time series software fits both submodels simultaneously. 8 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II In SAS: proc autoreg can handle AR(p) errors, but not ARMA(p; q) for q > 0. proc arima can handle ARMA(p; q). In R, try AR(1) errors: ar1 <- arima(sales$SALES, order = c(1, 0, 0), xreg = sales$T) print(ar1) tsdiag(ar1) The ARMA(p; q) model is specified by order = c(p, 0, q). The middle part of the order is d, for differencing. 9 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Note that φ^, the ar1 coefficient, is significantly different from zero. Note that the trend (coefficient of T) is similar to the original regression: 4.2959 versus 4.2956. Its reported standard error is higher: 0.1760 versus 0.1069. The original, smaller, standard error is not credible, because it was calculated on the assumption that the residuals are not correlated. The new standard error recognizes autocorrelation, and is more credible, but is still calculated on an assumption: that the residuals are AR(1). 10 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Which model to use? ACF of sales residuals decays something like an exponential, but is also not significantly different from zero for m > 1, so it could be MA(1). ma1 <- arima(sales$SALES, order = c(0, 0, 1), xreg = sales$T) print(ma1) tsdiag(ma1) ^ θ1, the ma1 coefficient, is also significantly different from zero. But AIC is higher than for AR(1), so AR(1) is preferred. 11 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Be systematic; use BIC to find a good model: P <- Q <- 0:3 BICtable <- matrix(NA, length(P), length(Q)) dimnames(BICtable) <- list(paste("p:", P), paste("q:", Q)) for (p in P) for (q in Q) { apq <- arima(sales$SALES, order = c(p, 0, q), xreg = sales$T) BICtable[p+1, q+1] <- AIC(apq, k = log(nrow(sales))) } BICtable As usual, use k = log(nrow(...)) to get BIC instead of AIC. As in stepwise regression, minimizing AIC tends to overfit. AR(1) gives the minimum BIC out of these choices. 12 / 1 Time series Autocorrelation ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Forecasting with(sales, plot(T, SALES, xlim = c(0, 40), ylim = c(0, 200))) ar1Fit <- coefficients(ar1)["intercept"] + coefficients(ar1)["sales$T"] * sales$T lines(sales$T, ar1Fit, lty = 2) newTimes <- 36:40 p <- predict(ar1, n.ahead = length(newTimes), newxreg = newTimes) pCL <- p$se * qnorm(.975) matlines(newTimes, p$pred + cbind(0, -pCL, pCL), col = c("red", "blue", "blue"), lty = c(2, 3, 3)) 13 / 1 Time series Autocorrelation.
Load more

Recommended publications
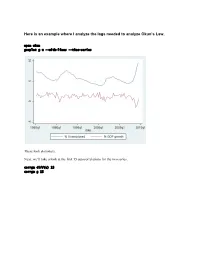
  • Here Is an Example Where I Analyze the Lags Needed to Analyze Okun's
    Here is an example where I analyze the lags needed to analyze Okun’s Law. open okun gnuplot g u --with-lines --time-series These look stationary. Next, we’ll take a look at the first 15 autocorrelations for the two series. corrgm diff(u) 15 corrgm g 15 These are autocorrelated and so are these. I would expect that a simple regression will not be sufficient to model this relationship. Let’s try anyway. Run a simple regression and look at the residuals ols diff(u) const g series ehat=$uhat gnuplot ehat --with-lines --time-series These look positively autocorrelated to me. Notice how the residuals fall below zero for a while, then rise above for a while, and repeat this pattern. Take a look at the correlogram. The first autocorrelation is significant. More lags of D.u or g will probably fix this. LM test of residuals smpl 1985.2 2009.3 ols diff(u) const g modeltab add modtest 1 --autocorr --quiet modtest 2 --autocorr --quiet modtest 3 --autocorr --quiet modtest 4 --autocorr --quiet Breusch-Godfrey test for first-order autocorrelation Alternative statistic: TR^2 = 6.576105, with p-value = P(Chi-square(1) > 6.5761) = 0.0103 Breusch-Godfrey test for autocorrelation up to order 2 Alternative statistic: TR^2 = 7.922218, with p-value = P(Chi-square(2) > 7.92222) = 0.019 Breusch-Godfrey test for autocorrelation up to order 3 Alternative statistic: TR^2 = 11.200978, with p-value = P(Chi-square(3) > 11.201) = 0.0107 Breusch-Godfrey test for autocorrelation up to order 4 Alternative statistic: TR^2 = 11.220956, with p-value = P(Chi-square(4) > 11.221) = 0.0242 Yep, that’s not too good.
    [Show full text]
  • Kalman and Particle Filtering
    Abstract: The Kalman and Particle filters are algorithms that recursively update an estimate of the state and find the innovations driving a stochastic process given a sequence of observations. The Kalman filter accomplishes this goal by linear projections, while the Particle filter does so by a sequential Monte Carlo method. With the state estimates, we can forecast and smooth the stochastic process. With the innovations, we can estimate the parameters of the model. The article discusses how to set a dynamic model in a state-space form, derives the Kalman and Particle filters, and explains how to use them for estimation. Kalman and Particle Filtering The Kalman and Particle filters are algorithms that recursively update an estimate of the state and find the innovations driving a stochastic process given a sequence of observations. The Kalman filter accomplishes this goal by linear projections, while the Particle filter does so by a sequential Monte Carlo method. Since both filters start with a state-space representation of the stochastic processes of interest, section 1 presents the state-space form of a dynamic model. Then, section 2 intro- duces the Kalman filter and section 3 develops the Particle filter. For extended expositions of this material, see Doucet, de Freitas, and Gordon (2001), Durbin and Koopman (2001), and Ljungqvist and Sargent (2004). 1. The state-space representation of a dynamic model A large class of dynamic models can be represented by a state-space form: Xt+1 = ϕ (Xt,Wt+1; γ) (1) Yt = g (Xt,Vt; γ) . (2) This representation handles a stochastic process by finding three objects: a vector that l describes the position of the system (a state, Xt X R ) and two functions, one mapping ∈ ⊂ 1 the state today into the state tomorrow (the transition equation, (1)) and one mapping the state into observables, Yt (the measurement equation, (2)).
    [Show full text]
  • Lecture 19: Wavelet Compression of Time Series and Images
    Lecture 19: Wavelet compression of time series and images c Christopher S. Bretherton Winter 2014 Ref: Matlab Wavelet Toolbox help. 19.1 Wavelet compression of a time series The last section of wavelet leleccum notoolbox.m demonstrates the use of wavelet compression on a time series. The idea is to keep the wavelet coefficients of largest amplitude and zero out the small ones. 19.2 Wavelet analysis/compression of an image Wavelet analysis is easily extended to two-dimensional images or datasets (data matrices), by first doing a wavelet transform of each column of the matrix, then transforming each row of the result (see wavelet image). The wavelet coeffi- cient matrix has the highest level (largest-scale) averages in the first rows/columns, then successively smaller detail scales further down the rows/columns. The ex- ample also shows fine results with 50-fold data compression. 19.3 Continuous Wavelet Transform (CWT) Given a continuous signal u(t) and an analyzing wavelet (x), the CWT has the form Z 1 s − t W (λ, t) = λ−1=2 ( )u(s)ds (19.3.1) −∞ λ Here λ, the scale, is a continuous variable. We insist that have mean zero and that its square integrates to 1. The continuous Haar wavelet is defined: 8 < 1 0 < t < 1=2 (t) = −1 1=2 < t < 1 (19.3.2) : 0 otherwise W (λ, t) is proportional to the difference of running means of u over successive intervals of length λ/2. 1 Amath 482/582 Lecture 19 Bretherton - Winter 2014 2 In practice, for a discrete time series, the integral is evaluated as a Riemann sum using the Matlab wavelet toolbox function cwt.
    [Show full text]
  • Power Comparisons of Five Most Commonly Used Autocorrelation Tests
    Pak.j.stat.oper.res. Vol.16 No. 1 2020 pp119-130 DOI: http://dx.doi.org/10.18187/pjsor.v16i1.2691 Pakistan Journal of Statistics and Operation Research Power Comparisons of Five Most Commonly Used Autocorrelation Tests Stanislaus S. Uyanto School of Economics and Business, Atma Jaya Catholic University of Indonesia, [email protected] Abstract In regression analysis, autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated. The consequence is that the estimates of coefficients and their standard errors will be wrong if the autocorrelation is ignored. There are many tests for autocorrelation, we want to know which test is more powerful. We use Monte Carlo methods to compare the power of five most commonly used tests for autocorrelation, namely Durbin-Watson, Breusch-Godfrey, Box–Pierce, Ljung Box, and Runs tests in two different linear regression models. The results indicate the Durbin-Watson test performs better in the regression model without lagged dependent variable, although the advantage over the other tests reduce with increasing autocorrelation and sample sizes. For the model with lagged dependent variable, the Breusch-Godfrey test is generally superior to the other tests. Key Words: Correlated error terms; Ordinary least squares assumption; Residuals; Regression diagnostic; Lagged dependent variable. Mathematical Subject Classification: 62J05; 62J20. 1. Introduction An important assumption of the classical linear regression model states that there is no autocorrelation in the error terms. Autocorrelation of the error terms violates the ordinary least squares assumption that the error terms are uncorrelated, meaning that the Gauss Markov theorem (Plackett, 1949, 1950; Greene, 2018) does not apply, and that ordinary least squares estimators are no longer the best linear unbiased estimators.
    [Show full text]
  • LECTURES 2 - 3 : Stochastic Processes, Autocorrelation Function
    LECTURES 2 - 3 : Stochastic Processes, Autocorrelation function. Stationarity. Important points of Lecture 1: A time series fXtg is a series of observations taken sequentially over time: xt is an observation recorded at a specific time t. Characteristics of times series data: observations are dependent, become available at equally spaced time points and are time-ordered. This is a discrete time series. The purposes of time series analysis are to model and to predict or forecast future values of a series based on the history of that series. 2.2 Some descriptive techniques. (Based on [BD] x1.3 and x1.4) ......................................................................................... Take a step backwards: how do we describe a r.v. or a random vector? ² for a r.v. X: 2 d.f. FX (x) := P (X · x), mean ¹ = EX and variance σ = V ar(X). ² for a r.vector (X1;X2): joint d.f. FX1;X2 (x1; x2) := P (X1 · x1;X2 · x2), marginal d.f.FX1 (x1) := P (X1 · x1) ´ FX1;X2 (x1; 1) 2 2 mean vector (¹1; ¹2) = (EX1; EX2), variances σ1 = V ar(X1); σ2 = V ar(X2), and covariance Cov(X1;X2) = E(X1 ¡ ¹1)(X2 ¡ ¹2) ´ E(X1X2) ¡ ¹1¹2. Often we use correlation = normalized covariance: Cor(X1;X2) = Cov(X1;X2)=fσ1σ2g ......................................................................................... To describe a process X1;X2;::: we define (i) Def. Distribution function: (fi-di) d.f. Ft1:::tn (x1; : : : ; xn) = P (Xt1 · x1;:::;Xtn · xn); i.e. this is the joint d.f. for the vector (Xt1 ;:::;Xtn ). (ii) First- and Second-order moments. ² Mean: ¹X (t) = EXt 2 2 2 2 ² Variance: σX (t) = E(Xt ¡ ¹X (t)) ´ EXt ¡ ¹X (t) 1 ² Autocovariance function: γX (t; s) = Cov(Xt;Xs) = E[(Xt ¡ ¹X (t))(Xs ¡ ¹X (s))] ´ E(XtXs) ¡ ¹X (t)¹X (s) (Note: this is an infinite matrix).
    [Show full text]
  • Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients
    Alternative Tests for Time Series Dependence Based on Autocorrelation Coefficients Richard M. Levich and Rosario C. Rizzo * Current Draft: December 1998 Abstract: When autocorrelation is small, existing statistical techniques may not be powerful enough to reject the hypothesis that a series is free of autocorrelation. We propose two new and simple statistical tests (RHO and PHI) based on the unweighted sum of autocorrelation and partial autocorrelation coefficients. We analyze a set of simulated data to show the higher power of RHO and PHI in comparison to conventional tests for autocorrelation, especially in the presence of small but persistent autocorrelation. We show an application of our tests to data on currency futures to demonstrate their practical use. Finally, we indicate how our methodology could be used for a new class of time series models (the Generalized Autoregressive, or GAR models) that take into account the presence of small but persistent autocorrelation. _______________________________________________________________ An earlier version of this paper was presented at the Symposium on Global Integration and Competition, sponsored by the Center for Japan-U.S. Business and Economic Studies, Stern School of Business, New York University, March 27-28, 1997. We thank Paul Samuelson and the other participants at that conference for useful comments. * Stern School of Business, New York University and Research Department, Bank of Italy, respectively. 1 1. Introduction Economic time series are often characterized by positive
    [Show full text]
  • 3 Autocorrelation
    3 Autocorrelation Autocorrelation refers to the correlation of a time series with its own past and future values. Autocorrelation is also sometimes called “lagged correlation” or “serial correlation”, which refers to the correlation between members of a series of numbers arranged in time. Positive autocorrelation might be considered a specific form of “persistence”, a tendency for a system to remain in the same state from one observation to the next. For example, the likelihood of tomorrow being rainy is greater if today is rainy than if today is dry. Geophysical time series are frequently autocorrelated because of inertia or carryover processes in the physical system. For example, the slowly evolving and moving low pressure systems in the atmosphere might impart persistence to daily rainfall. Or the slow drainage of groundwater reserves might impart correlation to successive annual flows of a river. Or stored photosynthates might impart correlation to successive annual values of tree-ring indices. Autocorrelation complicates the application of statistical tests by reducing the effective sample size. Autocorrelation can also complicate the identification of significant covariance or correlation between time series (e.g., precipitation with a tree-ring series). Autocorrelation implies that a time series is predictable, probabilistically, as future values are correlated with current and past values. Three tools for assessing the autocorrelation of a time series are (1) the time series plot, (2) the lagged scatterplot, and (3) the autocorrelation function. 3.1 Time series plot Positively autocorrelated series are sometimes referred to as persistent because positive departures from the mean tend to be followed by positive depatures from the mean, and negative departures from the mean tend to be followed by negative departures (Figure 3.1).
    [Show full text]
  • Time Series: Co-Integration
    Time Series: Co-integration Series: Economic Forecasting; Time Series: General; Watson M W 1994 Vector autoregressions and co-integration. Time Series: Nonstationary Distributions and Unit In: Engle R F, McFadden D L (eds.) Handbook of Econo- Roots; Time Series: Seasonal Adjustment metrics Vol. IV. Elsevier, The Netherlands N. H. Chan Bibliography Banerjee A, Dolado J J, Galbraith J W, Hendry D F 1993 Co- Integration, Error Correction, and the Econometric Analysis of Non-stationary Data. Oxford University Press, Oxford, UK Time Series: Cycles Box G E P, Tiao G C 1977 A canonical analysis of multiple time series. Biometrika 64: 355–65 Time series data in economics and other fields of social Chan N H, Tsay R S 1996 On the use of canonical correlation science often exhibit cyclical behavior. For example, analysis in testing common trends. In: Lee J C, Johnson W O, aggregate retail sales are high in November and Zellner A (eds.) Modelling and Prediction: Honoring December and follow a seasonal cycle; voter regis- S. Geisser. Springer-Verlag, New York, pp. 364–77 trations are high before each presidential election and Chan N H, Wei C Z 1988 Limiting distributions of least squares follow an election cycle; and aggregate macro- estimates of unstable autoregressive processes. Annals of Statistics 16: 367–401 economic activity falls into recession every six to eight Engle R F, Granger C W J 1987 Cointegration and error years and follows a business cycle. In spite of this correction: Representation, estimation, and testing. Econo- cyclicality, these series are not perfectly predictable, metrica 55: 251–76 and the cycles are not strictly periodic.
    [Show full text]
  • Spatial Autocorrelation: Covariance and Semivariance Semivariance
    Spatial Autocorrelation: Covariance and Semivariancence Lily Housese ­P eters GEOG 593 November 10, 2009 Quantitative Terrain Descriptorsrs Covariance and Semivariogram areare numericc methods used to describe the character of the terrain (ex. Terrain roughness, irregularity) Terrain character has important implications for: 1. the type of sampling strategy chosen 2. estimating DTM accuracy (after sampling and reconstruction) Spatial Autocorrelationon The First Law of Geography ““ Everything is related to everything else, but near things are moo re related than distant things.” (Waldo Tobler) The value of a variable at one point in space is related to the value of that same variable in a nearby location Ex. Moranan ’s I, Gearyary ’s C, LISA Positive Spatial Autocorrelation (Neighbors are similar) Negative Spatial Autocorrelation (Neighbors are dissimilar) R(d) = correlation coefficient of all the points with horizontal interval (d) Covariance The degree of similarity between pairs of surface points The value of similarity is an indicator of the complexity of the terrain surface Smaller the similarity = more complex the terrain surface V = Variance calculated from all N points Cov (d) = Covariance of all points with horizontal interval d Z i = Height of point i M = average height of all points Z i+d = elevation of the point with an interval of d from i Semivariancee Expresses the degree of relationship between points on a surface Equal to half the variance of the differences between all possible points spaced a constant distance apart
    [Show full text]
  • Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique
    Modeling and Generating Multivariate Time Series with Arbitrary Marginals Using a Vector Autoregressive Technique Bahar Deler Barry L. Nelson Dept. of IE & MS, Northwestern University September 2000 Abstract We present a model for representing stationary multivariate time series with arbitrary mar- ginal distributions and autocorrelation structures and describe how to generate data quickly and accurately to drive computer simulations. The central idea is to transform a Gaussian vector autoregressive process into the desired multivariate time-series input process that we presume as having a VARTA (Vector-Autoregressive-To-Anything) distribution. We manipulate the correlation structure of the Gaussian vector autoregressive process so that we achieve the desired correlation structure for the simulation input process. For the purpose of computational efficiency, we provide a numerical method, which incorporates a numerical-search procedure and a numerical-integration technique, for solving this correlation-matching problem. Keywords: Computer simulation, vector autoregressive process, vector time series, multivariate input mod- eling, numerical integration. 1 1 Introduction Representing the uncertainty or randomness in a simulated system by an input model is one of the challenging problems in the practical application of computer simulation. There are an abundance of examples, from manufacturing to service applications, where input modeling is critical; e.g., modeling the time to failure for a machining process, the demand per unit time for inventory of a product, or the times between arrivals of calls to a call center. Further, building a large- scale discrete-event stochastic simulation model may require the development of a large number of, possibly multivariate, input models. Development of these models is facilitated by accurate and automated (or nearly automated) input modeling support.
    [Show full text]
  • Statistical Tool for Soil Biology : 11. Autocorrelogram and Mantel Test
    ‘i Pl w f ’* Em J. 1996, (4), i Soil BioZ., 32 195-203 Statistical tool for soil biology. XI. Autocorrelogram and Mantel test Jean-Pierre Rossi Laboratoire d Ecologie des Sols Trofiicaux, ORSTOM/Université Paris 6, 32, uv. Varagnat, 93143 Bondy Cedex, France. E-mail: rossij@[email protected]. fr. Received October 23, 1996; accepted March 24, 1997. Abstract Autocorrelation analysis by Moran’s I and the Geary’s c coefficients is described and illustrated by the analysis of the spatial pattern of the tropical earthworm Clzuniodrilus ziehe (Eudrilidae). Simple and partial Mantel tests are presented and illustrated through the analysis various data sets. The interest of these methods for soil ecology is discussed. Keywords: Autocorrelation, correlogram, Mantel test, geostatistics, spatial distribution, earthworm, plant-parasitic nematode. L’outil statistique en biologie du sol. X.?. Autocorrélogramme et test de Mantel. Résumé L’analyse de l’autocorrélation par les indices I de Moran et c de Geary est décrite et illustrée à travers l’analyse de la distribution spatiale du ver de terre tropical Chuniodi-ibs zielae (Eudrilidae). Les tests simple et partiel de Mantel sont présentés et illustrés à travers l’analyse de jeux de données divers. L’intérêt de ces méthodes en écologie du sol est discuté. Mots-clés : Autocorrélation, corrélogramme, test de Mantel, géostatistiques, distribution spatiale, vers de terre, nématodes phytoparasites. INTRODUCTION the variance that appear to be related by a simple power law. The obvious interest of that method is Spatial heterogeneity is an inherent feature of that samples from various sites can be included in soil faunal communities with significant functional the analysis.
    [Show full text]
  • Applied Time Series Analysis
    Applied Time Series Analysis SS 2018 February 12, 2018 Dr. Marcel Dettling Institute for Data Analysis and Process Design Zurich University of Applied Sciences CH-8401 Winterthur Table of Contents 1 INTRODUCTION 1 1.1 PURPOSE 1 1.2 EXAMPLES 2 1.3 GOALS IN TIME SERIES ANALYSIS 8 2 MATHEMATICAL CONCEPTS 11 2.1 DEFINITION OF A TIME SERIES 11 2.2 STATIONARITY 11 2.3 TESTING STATIONARITY 13 3 TIME SERIES IN R 15 3.1 TIME SERIES CLASSES 15 3.2 DATES AND TIMES IN R 17 3.3 DATA IMPORT 21 4 DESCRIPTIVE ANALYSIS 23 4.1 VISUALIZATION 23 4.2 TRANSFORMATIONS 26 4.3 DECOMPOSITION 29 4.4 AUTOCORRELATION 50 4.5 PARTIAL AUTOCORRELATION 66 5 STATIONARY TIME SERIES MODELS 69 5.1 WHITE NOISE 69 5.2 ESTIMATING THE CONDITIONAL MEAN 70 5.3 AUTOREGRESSIVE MODELS 71 5.4 MOVING AVERAGE MODELS 85 5.5 ARMA(P,Q) MODELS 93 6 SARIMA AND GARCH MODELS 99 6.1 ARIMA MODELS 99 6.2 SARIMA MODELS 105 6.3 ARCH/GARCH MODELS 109 7 TIME SERIES REGRESSION 113 7.1 WHAT IS THE PROBLEM? 113 7.2 FINDING CORRELATED ERRORS 117 7.3 COCHRANE‐ORCUTT METHOD 124 7.4 GENERALIZED LEAST SQUARES 125 7.5 MISSING PREDICTOR VARIABLES 131 8 FORECASTING 137 8.1 STATIONARY TIME SERIES 138 8.2 SERIES WITH TREND AND SEASON 145 8.3 EXPONENTIAL SMOOTHING 152 9 MULTIVARIATE TIME SERIES ANALYSIS 161 9.1 PRACTICAL EXAMPLE 161 9.2 CROSS CORRELATION 165 9.3 PREWHITENING 168 9.4 TRANSFER FUNCTION MODELS 170 10 SPECTRAL ANALYSIS 175 10.1 DECOMPOSING IN THE FREQUENCY DOMAIN 175 10.2 THE SPECTRUM 179 10.3 REAL WORLD EXAMPLE 186 11 STATE SPACE MODELS 187 11.1 STATE SPACE FORMULATION 187 11.2 AR PROCESSES WITH MEASUREMENT NOISE 188 11.3 DYNAMIC LINEAR MODELS 191 ATSA 1 Introduction 1 Introduction 1.1 Purpose Time series data, i.e.
    [Show full text]