The Angular Diameter of Lambda Bootis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Astronomy 114 Problem Set # 2 Due: 16 Feb 2007 Name
Astronomy 114 Problem Set # 2 Due: 16 Feb 2007 Name: SOLUTIONS As we discussed in class, most angles encountered in astronomy are quite small so degrees are often divded into 60 minutes and, if necessary, minutes in 60 seconds. Therefore to convert an angle measured in degrees to minutes, multiply by 60. To convert minutes to seconds, multiply by 60. To use trigonometric formulae, angles might have to be written in terms of radians. Recall that 2π radians = 360 degrees. Therefore, to convert degrees to radians, multiply by 2π/360. 1 The average angular diameter of the Moon is 0.52 degrees. What is the angular diameter of the moon in minutes? The goal here is to change units from degrees to minutes. 0.52 degrees 60 minutes = 31.2 minutes 1 degree 2 The mean angular diameter of the Sun is 32 minutes. What is the angular diameter of the Sun in degrees? 32 minutes 1 degrees =0.53 degrees 60 minutes 0.53 degrees 2π =0.0093 radians 360 degrees Note that the angular diameter of the Sun is nearly the same as the angular diameter of the Moon. This similarity explains why sometimes an eclipse of the Sun by the Moon is total and sometimes is annular. See Chap. 3 for more details. 3 Early astronomers measured the Sun’s physical diameter to be roughly 109 Earth diameters (1 Earth diameter is 12,750 km). Calculate the average distance to the Sun using trigonometry. (Hint: because the angular size is small, you can make the approximation that sin α = α but don’t forget to express α in radians!). -

Orbit of the Mercury-Manganese Binary 41 Eridani? C
A&A 600, L5 (2017) Astronomy DOI: 10.1051/0004-6361/201730414 & c ESO 2017 Astrophysics Letter to the Editor Orbit of the mercury-manganese binary 41 Eridani? C. A. Hummel1, M. Schöller1, G. Duvert2, and S. Hubrig3 1 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany e-mail: [email protected] 2 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble, UMR 5274, 38041 Grenoble, France 3 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany Received 10 January 2017 / Accepted 1 March 2017 ABSTRACT Context. Mercury-manganese (HgMn) stars are a class of slowly rotating chemically peculiar main-sequence late B-type stars. More than two-thirds of the HgMn stars are known to belong to spectroscopic binaries. Aims. By determining orbital solutions for binary HgMn stars, we will be able to obtain the masses for both components and the distance to the system. Consequently, we can establish the position of both components in the Hertzsprung-Russell diagram and confront the chemical peculiarities of the HgMn stars with their age and evolutionary history. Methods. We initiated a program to identify interferometric binaries in a sample of HgMn stars, using the PIONIER near-infrared interferometer at the VLTI on Cerro Paranal, Chile. For the detected systems, we intend to obtain full orbital solutions in conjunction with spectroscopic data. Results. The data obtained for the SB2 system 41 Eridani allowed the determination of the orbital elements with a period of just five days and a semi-major axis of under 2 mas. -

N O T I C E This Document Has Been Reproduced From
N O T I C E THIS DOCUMENT HAS BEEN REPRODUCED FROM MICROFICHE. ALTHOUGH IT IS RECOGNIZED THAT CERTAIN PORTIONS ARE ILLEGIBLE, IT IS BEING RELEASED IN THE INTEREST OF MAKING AVAILABLE AS MUCH INFORMATION AS POSSIBLE P993-198422 International Collogium on Atomic Spectra and Oscillator Strengths for Astrophysical and Laboratory Plasmas (4th) Held at the National institute of Standards and Technology Gaithersburg, Maryland on September 14-17, 1992 (U.S.) National inst. of Standards and Technology (PL) Gaithersburg, MD Apr 93 US. DEPARTMENT OF COMMERCE Ndioul Techcical IMermeNON Service B•11G 2-10i1A2 2 MIST-1 /4 U.S. VZPARTMENT OF COMMERCE (REV. NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY M GONTSOLw1N^BENN O4" COMM 4M /. MANUSCRIPT REVIEW AND APPROVAL "KIST/ p-850 ^' THIS NSTRUCTWNS: ATTACH ORIGINAL OF FORM TO ONE (1) COPY OF MANUSCIIN IT AND SEINE TO: PUBLICATIOM OATS NUMBER PRINTED PAGES April 1993 199 HE SECRETAIIY, APPROPRIATE EDITO RIAL REVIEW BOARD. ITLE AND SUBTITLE (CITE NN PULL) 4rh International Colloquium on Atomic Spectra and Oscillator Strengths for Astrophysical and Laboratory Plasmas -- POSTER PAPERS :ONTIEACT OR GRANT NUMBER TYPE OF REPORT AND/OR PERIOD COMM UTHOR(S) (LAST %,TAME, POST NNITIAL, SECOND INITIAL) PERFORM" ORGANIZATION (CHECK (IQ ONE SOX) EDITORS XXX MIST/GAITHERSBUIIG Sugar, Jack and Leckrone, B:;vid INST/BODUM JILA BOIRDE11 "ORATORY AND DIVISION NAMES (FIRST MOST AUTHOR ONLY) Physics Laboratory/Atomic Physics Division 'PONSORING ORGANIZATION NAME AND COMPLETE ADDRESS TREET, CITY. STATE. ZNh ^y((S/ ,T AiL7A - -ASO IECOMMENDsO FOR MIST PUBLICATION JOVIAMAL OF RESEMICM (MIST JRES) CIONOGRAPK (MIST MN) LETTER CIRCULAR J. PHYS. A CHEM. -

Chandra X-Ray Study Confirms That the Magnetic Standard Ap Star KQ Vel
A&A 641, L8 (2020) Astronomy https://doi.org/10.1051/0004-6361/202038214 & c ESO 2020 Astrophysics LETTER TO THE EDITOR Chandra X-ray study confirms that the magnetic standard Ap star KQ Vel hosts a neutron star companion? Lidia M. Oskinova1,2, Richard Ignace3, Paolo Leto4, and Konstantin A. Postnov5,2 1 Institute for Physics and Astronomy, University Potsdam, 14476 Potsdam, Germany e-mail: [email protected] 2 Department of Astronomy, Kazan Federal University, Kremlevskaya Str 18, Kazan, Russia 3 Department of Physics & Astronomy, East Tennessee State University, Johnson City, TN 37614, USA 4 NAF – Osservatorio Astrofisico di Catania, Via S. Sofia 78, 95123 Catania, Italy 5 Sternberg Astronomical Institute, M.V. Lomonosov Moscow University, Universitetskij pr. 13, 119234 Moscow, Russia Received 20 April 2020 / Accepted 20 July 2020 ABSTRACT Context. KQ Vel is a peculiar A0p star with a strong surface magnetic field of about 7.5 kG. It has a slow rotational period of nearly 8 years. Bailey et al. (A&A, 575, A115) detected a binary companion of uncertain nature and suggested that it might be a neutron star or a black hole. Aims. We analyze X-ray data obtained by the Chandra telescope to ascertain information about the stellar magnetic field and/or interaction between the star and its companion. Methods. We confirm previous X-ray detections of KQ Vel with a relatively high X-ray luminosity of 2 × 1030 erg s−1. The X-ray spectra suggest the presence of hot gas at >20 MK and, possibly, of a nonthermal component. -

Planetary Diameters in the Sürya-Siddhänta DR
Planetary Diameters in the Sürya-siddhänta DR. RICHARD THOMPSON Bhaktivedanta Institute, P.O. Box 52, Badger, CA 93603 Abstract. This paper discusses a rule given in the Indian astronomical text Sürya-siddhänta for comput- ing the angular diameters of the planets. I show that this text indicates a simple formula by which the true diameters of these planets can be computed from their stated angular diameters. When these computations are carried out, they give values for the planetary diameters that agree surprisingly well with modern astronomical data. I discuss several possible explanations for this, and I suggest that the angular diameter rule in the Sürya-siddhänta may be based on advanced astronomical knowledge that was developed in ancient times but has now been largely forgotten. In chapter 7 of the Sürya-siddhänta, the 13th çloka gives the following rule for calculating the apparent diameters of the planets Mars, Saturn, Mercury, Jupiter, and Venus: 7.13. The diameters upon the moon’s orbit of Mars, Saturn, Mercury, and Jupiter, are de- clared to be thirty, increased successively by half the half; that of Venus is sixty.1 The meaning is as follows: The diameters are measured in a unit of distance called the yojana, which in the Sürya-siddhänta is about five miles. The phrase “upon the moon’s orbit” means that the planets look from our vantage point as though they were globes of the indicated diameters situated at the distance of the moon. (Our vantage point is ideally the center of the earth.) Half the half of 30 is 7.5. -

Radio Astronomy
Edition of 2013 HANDBOOK ON RADIO ASTRONOMY International Telecommunication Union Sales and Marketing Division Place des Nations *38650* CH-1211 Geneva 20 Switzerland Fax: +41 22 730 5194 Printed in Switzerland Tel.: +41 22 730 6141 Geneva, 2013 E-mail: [email protected] ISBN: 978-92-61-14481-4 Edition of 2013 Web: www.itu.int/publications Photo credit: ATCA David Smyth HANDBOOK ON RADIO ASTRONOMY Radiocommunication Bureau Handbook on Radio Astronomy Third Edition EDITION OF 2013 RADIOCOMMUNICATION BUREAU Cover photo: Six identical 22-m antennas make up CSIRO's Australia Telescope Compact Array, an earth-rotation synthesis telescope located at the Paul Wild Observatory. Credit: David Smyth. ITU 2013 All rights reserved. No part of this publication may be reproduced, by any means whatsoever, without the prior written permission of ITU. - iii - Introduction to the third edition by the Chairman of ITU-R Working Party 7D (Radio Astronomy) It is an honour and privilege to present the third edition of the Handbook – Radio Astronomy, and I do so with great pleasure. The Handbook is not intended as a source book on radio astronomy, but is concerned principally with those aspects of radio astronomy that are relevant to frequency coordination, that is, the management of radio spectrum usage in order to minimize interference between radiocommunication services. Radio astronomy does not involve the transmission of radiowaves in the frequency bands allocated for its operation, and cannot cause harmful interference to other services. On the other hand, the received cosmic signals are usually extremely weak, and transmissions of other services can interfere with such signals. -

Transit of Venus M
National Aeronautics and Space Administration The Transit of Venus June 5/6, 2012 HD209458b (HST) The Transit of Venus June 5/6, 2012 Transit of Venus Mathof Venus Transit Top Row – Left image - Photo taken at the US Naval Math Puzzler 3 - The duration of the transit depends Observatory of the 1882 transit of Venus. Middle on the relative speeds between the fast-moving image - The cover of Harpers Weekly for 1882 Venus in its orbit and the slower-moving Earth in its showing children watching the transit of Venus. orbit. This speed difference is known to be 5.24 km/sec. If the June 5, 2012, transit lasts 24,000 Right image – Image from NASA's TRACE satellite seconds, during which time the planet moves an of the transit of Venus, June 8, 2004. angular distance of 0.17 degrees across the sun as Middle - Geometric sketches of the transit of Venus viewed from Earth, what distance between Earth and by James Ferguson on June 6, 1761 showing the Venus allows the distance traveled by Venus along its shift in the transit chords depending on the orbit to subtend the observed angle? observer's location on Earth. The parallax angle is related to the distance between Earth and Venus. Determining the Astronomical Unit Bottom – Left image - NOAA GOES-12 satellite x-ray image showing the Transit of Venus 2004. Middle Based on the calculations of Nicolas Copernicus and image – An observer of the 2004 transit of Venus Johannes Kepler, the distances of the known planets wearing NASA’s Sun-Earth Day solar glasses for from the sun could be given rather precisely in terms safe viewing. -

Alpha Orionis (Betelgeuse)
AAVSO: Alpha Ori, December 2000 Variable Star Of The Month Variable Star Of The Month December, 2000: Alpha Orionis (Betelgeuse) Atmosphere of Betelgeuse - Alpha Orionis Hubble Space Telescope - Faint Object Camera January 15, 1996; A. Dupree (CfA), NASA, ESA From the city or country sky, from almost any part of the world, the majestic figure of Orion dominates overhead this time of year with his belt, sword, and club. High in his left shoulder (for those of us in the northern hemisphere) is the great red pulsating supergiant, Betelgeuse (Alpha Orionis 0549+07). Recently acquiring fame for being the first star to have its atmosphere directly imaged (shown above), Alpha Orionis has captivated observers’ attention for centuries. Betelgeuse's variability was first noticed by Sir John Herschel in 1836. In his Outlines of Astronomy, published in 1849, Herschel wrote “The variations of Alpha Orionis, which were most striking and unequivocal in the years 1836-1840, within the years since elapsed became much less conspicuous…” In 1849 the variations again began to increase in amplitude, and in December 1852 it was thought by Herschel to be “actually the largest [brightest] star in the northern hemisphere”. Indeed, when at maximum, Betelgeuse sometimes rises to magnitude 0.4 when it becomes a fierce competitor to Rigel; in 1839 and 1852 it was thought by some observers to be nearly the equal of Capella. Observations by the observers of the AAVSO indicate that Betelgeuse probably reached magnitude 0.2 in 1933 and again in 1942. At minimum brightness, as in 1927 and 1941, the magnitude may drop below 1.2. -

Measuring Angular Diameter Distances of Strong Gravitational Lenses
Prepared for submission to JCAP Measuring angular diameter distances of strong gravitational lenses I. Jeea, E. Komatsua;b, S. H. Suyuc aMax-Planck-Institut f¨urAstrophysik, Karl-Schwarzschild Str. 1, 85741 Garching, Germany bKavli Institute for the Physics and Mathematics of the Universe, Todai Institutes for Ad- vanced Study, the University of Tokyo, Kashiwa, Japan 277-8583 (Kavli IPMU, WPI) cInstitute of Astronomy and Astrophysics, Academia Sinica, P.O. Box 23-141, Taipei 10617, Taiwan E-mail: [email protected] Abstract. The distance-redshift relation plays a fundamental role in constraining cosmo- logical models. In this paper, we show that measurements of positions and time delays of strongly lensed images of a background galaxy, as well as those of the velocity dispersion and mass profile of a lens galaxy, can be combined to extract the angular diameter distance of the lens galaxy. Physically, as the velocity dispersion and the time delay give a gravitational potential (GM=r) and a mass (GM) of the lens, respectively, dividing them gives a physical size (r) of the lens. Comparing the physical size with the image positions of a lensed galaxy gives the angular diameter distance to the lens. A mismatch between the exact locations at which these measurements are made can be corrected by measuring a local slope of the mass profile. We expand on the original idea put forward by Paraficz and Hjorth, who analyzed singular isothermal lenses, by allowing for an arbitrary slope of a power-law spherical mass density profile, an external convergence, and an anisotropic velocity dispersion. -

Near-Infrared Mapping and Physical Properties of the Dwarf-Planet Ceres
A&A 478, 235–244 (2008) Astronomy DOI: 10.1051/0004-6361:20078166 & c ESO 2008 Astrophysics Near-infrared mapping and physical properties of the dwarf-planet Ceres B. Carry1,2,C.Dumas1,3,, M. Fulchignoni2, W. J. Merline4, J. Berthier5, D. Hestroffer5,T.Fusco6,andP.Tamblyn4 1 ESO, Alonso de Córdova 3107, Vitacura, Santiago de Chile, Chile e-mail: [email protected] 2 LESIA, Observatoire de Paris-Meudon, 5 place Jules Janssen, 92190 Meudon Cedex, France 3 NASA/JPL, MS 183-501, 4800 Oak Grove Drive, Pasadena, CA 91109-8099, USA 4 SwRI, 1050 Walnut St. # 300, Boulder, CO 80302, USA 5 IMCCE, Observatoire de Paris, CNRS, 77 Av. Denfert Rochereau, 75014 Paris, France 6 ONERA, BP 72, 923222 Châtillon Cedex, France Received 26 June 2007 / Accepted 6 November 2007 ABSTRACT Aims. We study the physical characteristics (shape, dimensions, spin axis direction, albedo maps, mineralogy) of the dwarf-planet Ceres based on high angular-resolution near-infrared observations. Methods. We analyze adaptive optics J/H/K imaging observations of Ceres performed at Keck II Observatory in September 2002 with an equivalent spatial resolution of ∼50 km. The spectral behavior of the main geological features present on Ceres is compared with laboratory samples. Results. Ceres’ shape can be described by an oblate spheroid (a = b = 479.7 ± 2.3km,c = 444.4 ± 2.1 km) with EQJ2000.0 spin α = ◦ ± ◦ δ =+ ◦ ± ◦ . +0.000 10 vector coordinates 0 288 5 and 0 66 5 . Ceres sidereal period is measured to be 9 074 10−0.000 14 h. We image surface features with diameters in the 50–180 km range and an albedo contrast of ∼6% with respect to the average Ceres albedo. -
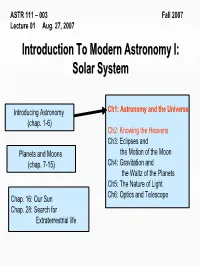
Astronomy and the Universe (Pdf)
ASTR 111 – 003 Fall 2007 Lecture 01 Aug. 27, 2007 IntroductionIntroduction ToTo ModernModern AstronomyAstronomy I:I: SolarSolar SystemSystem Introducing Astronomy Ch1: Astronomy and the Universe (chap. 1-6) Ch2: Knowing the Heavens Ch3: Eclipses and Planets and Moons the Motion of the Moon (chap. 7-15) Ch4: Gravitation and the Waltz of the Planets Ch5: The Nature of Light Chap. 16: Our Sun Ch6: Optics and Telescope Chap. 28: Search for Extraterrestrial life HighlightsHighlights A total lunar eclipse Tuesday morning, Aug. 28, 2007 EDT PDT – Partial eclipse begins: 4:51 AM 1:51 AM – Total eclipse begins: 5:52 AM 2:52 AM – Total eclipse ends: ----- 4:23 AM – Partial eclipse end: ----- 5:24 AM Google Earth “searches” the sky. AstronomyAstronomy PicturePicture ofof thethe DayDay ((2007/08/27) HugeHuge VoidVoid inin DistantDistant UniverseUniverse TodayToday’’ss SunSun ((2007/08/27)2007/08/27) AstronomyAstronomy andand thethe UniverseUniverse ChapterChapter OneOne ScientificScientific MethodsMethods Scientific Method – based on observation, logic, and skepticism Hypothesis – a collection of ideas that seems to explain a phenomenon Model – hypotheses that have withstood observational or experimental tests Theory – a body of related hypotheses can be pieced together into a self consistent description of nature Laws of Physics – theories that accurately describe the workings of physical reality, have stood the test of time and been shown to have great and general validity ExampleExample Theory: Earth and planets orbit the Sun due to the Sun’s gravitational attraction FFormationormation ofof SSolarolar SSystemystem The Sun and Planets to Scale – By exploring the planets, astronomers uncover clues about the formation of the solar system Terrestrial and Jovian Planets Meteorites. -

10252228.Pdf
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SEÇİLMİŞ BAZI PEKÜLER A YILDIZLARININ DOPPLER GÖRÜNTÜLEME YÖNTEMİ İLE YÜZEY HARİTALARININ ELDE EDİLMESİ S. Hande GÜRSOYTRAK ASTRONOMİ VE UZAY BİLİMLERİ ANABİLİM DALI ANKARA 2019 Her hakkı saklıdır ÖZET Doktora Tezi SEÇİLMİŞ BAZI PEKÜLER A YILDIZLARININ DOPPLER GÖRÜNTÜLEME YÖNTEMİ İLE YÜZEY HARİTALARININ ELDE EDİLMESİ S. Hande GÜRSOYTRAK Ankara Üniversitesi Fen Bilimleri Enstitüsü Astronomi ve Uzay Bilimleri Anabilim Dalı Danışman: Doç. Dr. Birol GÜROL Uzaklıkları nedeniyle ancak noktasal kaynak olarak görebildiğimiz yıldızların yüzeyindeki element bolluk dağılımlarının ortaya çıkarılabilmesi, astrofiziksel açıdan yıldızların iç dinamiklerinin anlaşılmasında son derece önemlidir. Bu çalışmada, A tayf türünden kimyasal peküler (Ap) yıldızlar; V776 Her, V354 Peg, 56 Tau ve EP UMa’nın tayfsal gözlemlerinden yararlanarak Doppler Görüntüleme tekniğiyle yüzey bollukları haritalandırılmıştır. Tayfsal gözlemler, TÜBİTAK Ulusal Gözlemevi (Antalya), 1.5 m’lik Rus-Türk Teleskobu’na bağlı (RTT150) Coude eşel tayfçekeri kullanılarak elde edilmiştir. Coude eşel tayfları 3690Å ile 10275Å dalgaboyu aralığını kapsamaktadır ve tayfsal çözünürlüğü 40000 civarındadır. Tayfların indirgenmesi IRAF (Image Reduction and Analysis Facility) programı kullanılarak gerçekleştirilmiştir. Çalışmanın temel hedefi olan Doppler görüntüleme tekniğinin gereksinimleri dikkate alınarak gözlemsel tayflar peküler yıldızların dönme dönemlerinin zaman serileri şeklinde alınmıştır. EP UMa için elde edilen tayf sayısı Doppler