DOCSLIB.ORG

Understanding Communities Via Hashtag Engagement: a Clustering Based Approach

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Understanding Communities Via Hashtag Engagement: a Clustering Based Approach Proceedings of the Tenth International AAAI Conference on Web and Social Media (ICWSM 2016) Understanding Communities via Hashtag Engagement: A Clustering Based Approach Orianna DeMasi ∗ Douglas Mason † Jeff Ma University of California, Berkeley Pinterest Twitter, Inc. Berkeley, CA 94720 San Francisco, CA 94103 San Francisco, CA 94103 [email protected] [email protected] [email protected] Abstract user experience, and hashtags can potentially enable such connections. Even though researchers have acknowledged We develop insight into community use of hashtags on so- cial media and find that hashtags with behavior indicative of this possibility (Laniado and Mika 2010; Russo and Nov real world communities are more engaging. To do this, we 2010), little research thus far has targeted understanding the study the relationship of hashtag usage with user engagement community use of hashtags. on Twitter. Hashtag engagement is useful as a surrogate mea- In this study we focus on how engaging different types of sure of how active community members are. We develop a hashtags are and consider relations with community metrics. framework for describing hashtag temporal usage, show the We find that hashtags that have a stronger resemblance to existence of 4 broad classes of hashtags, and show that the real world communities are more engaging. engagement of a hashtag varies significantly between classes. One of our contributions is a framework for understanding Periodically used hashtags, such as for TV shows and weekly community chats, are the most engaging, while hashtags re- different dynamic types of hashtags. With this framework, lating to events are the least engaging. Looking at how com- we unify previous work on identifying periodic hashtags munity dynamics vary within this framework reveals that a (Cook, Kenthapadi, and Mishra 2013) and event hashtags hashtag being used more frequently is not positively corre- (Cha et al. 2010; Lehmann et al. 2012; Crane and Sornette lated with it being more engaging. We then explore the pe- 2008; Lin et al. 2013; Shamma, Kennedy, and Churchill riodically used hashtags and find negative correlations with 2011). This unification validates previous observations that diversity of the user base, which implies concentrated com- there are coherent dynamic types of hashtags (Hsu, Chang, munities are the most engaging. We conclude by studying and Chen 2010; Romero, Meeder, and Kleinberg 2011). a set of community conversation-oriented hashtags and find Our second contribution is a set of analyses using this these hashtags to be more engaging than other hashtags, re- gardless of dynamic type. Our findings support the hypothe- framework on a comprehensive cohort dataset. We include sis that hashtags with stronger community behavior are more a comparison of engagement between hashtag types. Our engaging. analyses take steps in the direction of understanding engage- ment of hashtag types. This understanding is important, not just as a retrospective analysis, but as an actionable way for Introduction finding, connecting, and supporting communities. Hashtags have become a cornerstone of online social me- One of our findings is that periodically recurring hash- dia. From their birth on the Twitter platform, hashtags have tags are the most engaging type of hashtag, on average. Pre- evolved from their basic form of a short string of text pre- vious work that has analyzed peaks in hashtag usage, i.e. ceded by a pound symbol to be a tool for myriad purposes, events, is minimally actionable, as events are difficult to pre- e.g. ad campaigns and online chats (Yang et al. 2012). In ad- dict. In contrast, periodic events are predictable, so the abil- dition to being versatile, they are exceedingly popular and ity to identify and understand periodically used hashtags has have been adopted on nearly every social media platform. implications for how to design and implement new features While hashtags may have been introduced to catalog for social media. Such new features could include weekly information, they now can enable users to rally social checkins on relevant content or community features built up movements (e.g. #BlackLivesMatter a social movement for around a periodic event. By showing that periodically used racial justice), disseminate public health campaigns (e.g. hashtags are the most engaging, our work implies that sys- #ECigTruths from Chicago Department of Public Health), tems implemented around this periodic content would have and connect to communities (e.g. #RunChat a community the most impact. While our work focuses on hashtags, its for runners). Finding and connecting users to relevant com- broader implication is that systems designed to leverage pe- munities online is of paramount importance for improving riodic content to connect recurring communities will create a ∗Work does as intern as Twitter, Inc. more engaging experience than connecting more ephemeral †Work done as employee at Twitter, Inc. groups, e.g. groups that connect over events. Copyright c 2016, Association for the Advancement of Artificial The structure of this paper is as follows. We begin by Intelligence (www.aaai.org). All rights reserved. motivating the complexity of hashtags. We then propose a 102 framework for understanding coarse hashtag usage of all (Kouloumpis, Wilson, and Moore 2011; Davidov, Tsur, and popular hashtags. Using this framework, we show there Rappoport 2010) or political polarity (Conover et al. 2011). are 4 broad types of hashtags: events, stable, periodic, and Studies have also looked at hashtags themselves, both trying stochastic. These classes have been alluded to in prior work to understand their dynamics (Cha et al. 2010; Lehmann et (Hsu, Chang, and Chen 2010; Romero, Meeder, and Klein- al. 2012; Crane and Sornette 2008; Lin et al. 2013; Shamma, berg 2011), but this is the first systematic categorization val- Kennedy, and Churchill 2011; Yang and Leskovec 2011; idating their existence. We then propose a metric of engage- Hsu, Chang, and Chen 2010), popularity (Pervin et al. 2015; ment for a hashtag and study this metric within the different Ma, Sun, and Cong 2013; Tsur and Rappoport 2012), rel- hashtag types. We find hashtags with a recurring usage are at evance (Denton et al. 2015) and semantic meaning (Fer- least 6.5% more engaging than other types of hashtags and ragina, Piccinno, and Santoro 2015; Posch et al. 2013; over 100% more engaging than event hashtags, on average. Romero, Meeder, and Kleinberg 2011; Tsur, Littman, and We build models that consider the relationship of engage- Rappoport 2012). This work highlights the breadth and util- ment with Tweet volume, author diversity, and Tweet con- ity of hashtags as an important feature of social media. tent for each dynamic type. These models show that pop- Here, we are most interested in engagement of hashtags ular hashtags are not the most engaging and that low di- by type. We consider types to be classes of temporal usage versity groups can be particularly engaging. We then pro- patterns rather than a priori defined semantic or topic classes pose a refining framework that partitions the recurring hash- (Ferragina, Piccinno, and Santoro 2015; Posch et al. 2013; tags into 4 more interpretable classes: weekly events, all day Romero, Meeder, and Kleinberg 2011; Tsur, Littman, and weekly events, more frequent and less frequent than weekly Rappoport 2012). events. These subclusters reveal an even stronger negative Previous studies have looked at hashtag usage dynam- correlation of diversity with engagement for weekly events, ics and noted that there are different types. Some studies which implies that concentrated groups of users that con- have acknowledged at least three types of dynamics roughly vene weekly and tweet a lot about a shared interest generate falling into: continuous activity, periodic activity, or activity the most engaging hashtags. We conclude by examining en- concentrated around an isolated time domain. (Hsu, Chang, gagement for a particular subset of community conversation- and Chen 2010; Lehmann et al. 2012). However, these stud- oriented “chat” hashtags. ies did not provide a comprehensive framework for showing these classes exist or showing how to identify and catalog Contributions hashtags into each class. They also did not consider differ- ences in engagement between classes. Our contributions complement prior work that has looked at Other studies have focused on identifying and studying temporal usage of hashtags. We extend such work by pro- a single class of temporal dynamics. “Peaky” events, such viding a comprehensive categorization of dynamics and an- as news have been studied and classified into as many as 6 alyzing the implications for engagement and communities. types of classes (Cha et al. 2010; Lehmann et al. 2012; Crane We provide a novel comprehensive framework for clus- and Sornette 2008; Lin et al. 2013; Shamma, Kennedy, and tering hashtags based on temporal usage. We then analyze Churchill 2011; Yang and Leskovec 2011) . It has been sug- the resulting hashtag dynamic types, propose a metric of gested that these classes of events could relate to communi- engagement, and compare this metric of engagement be- ties if we consider a group of people interested in an event as tween the hashtag types. This comparison is an important a community. Here we are interested in considering commu- step for designing systems that is missing from prior work. nities as groups of users who continue to share relevant and We consider models that relate Tweet volume, author diver- specific information, say on a topic. Furthermore, studying sity, and Tweet content to hashtag engagement. We also pro- events is more retrospective and less actionable, as events pose and analyze another framework for understanding pe- are difficult to predict. riodic type hashtags and add a discussion of implications for Periodic hashtags, on the other hand, can be predicted and community engagement. Finally, we consider engagement thus could be actionable. Studies have briefly considered of community-oriented “chat” hashtags within this cluster- subsets from the class of periodic hashtags, for example pe- ing.
Load more

Recommended publications
  • Looking for Podcast Suggestions? We’Ve Got You Covered
    Looking for podcast suggestions? We’ve got you covered. We asked Loomis faculty members to share their podcast playlists with us, and they offered a variety of suggestions as wide-ranging as their areas of personal interest and professional expertise. Here’s a collection of 85 of these free, downloadable audio shows for you to try, listed alphabetically with their “recommenders” listed below each entry: 30 for 30 You may be familiar with ESPN’s 30 for 30 series of award-winning sports documentaries on television. The podcasts of the same name are audio documentaries on similarly compelling subjects. Recent podcasts have looked at the man behind the Bikram Yoga fitness craze, racial activism by professional athletes, the origins of the hugely profitable Ultimate Fighting Championship, and the lasting legacy of the John Madden Football video game. Recommended by Elliott: “I love how it involves the culture of sports. You get an inner look on a sports story or event that you never really knew about. Brings real life and sports together in a fantastic way.” 99% Invisible From the podcast website: “Ever wonder how inflatable men came to be regular fixtures at used car lots? Curious about the origin of the fortune cookie? Want to know why Sigmund Freud opted for a couch over an armchair? 99% Invisible is about all the thought that goes into the things we don’t think about — the unnoticed architecture and design that shape our world.” Recommended by Scott ABCA Calls from the Clubhouse Interviews with coaches in the American Baseball Coaches Association Recommended by Donnie, who is head coach of varsity baseball and says the podcast covers “all aspects of baseball, culture, techniques, practices, strategy, etc.
    [Show full text]
  • The Audience for Political Blogs NEW RESEARCH on BLOG READERSHIP
    IN COLLABORATION WITH: The Audience for Political Blogs NEW RESEARCH ON BLOG READERSHIP By Joseph Graf October 2006 The Graduate School of Political Management INSTITUTE FOR POLITICS, DEMOCRACY & THE INTERNET ACKNOWLEDGEMENTS This project was sponsored by @dvocacy Inc. and conducted by the Institute for Politics, Democracy & the Internet (IPDI). We are grateful to Roger Alan Stone, John Purcell, and Daniel Bennett for support and encouragement. IPDI is the premier research and advocacy center for the study and promotion of online politics in a manner that encourages citizen participation and improves governance – in short, to “de- mocratize democracy.” IPDI is non-partisan and non-profi t and is housed in GW’s Graduate School of Political Management. This project benefi ted from the advice and assistance of many individuals. We especially thank Chris Arterton and Henry Cope- land. This report was written by Joe Graf and edited by Carol Darr, director of IPDI, and Julie Germany, deputy director. Research assistance was provided by Chris Brooks, Peter Churchill, Riki Parikh, Ryan Sullivan, and Ed Trelinski. For more information about the Institute for Politics, Democ- racy & the Internet, visit www.ipdi.org. For more information about the Graduate School of Political Management, visit www.gwu.edu/~gspm. © GW’s Institute for Politics, Democracy & the Internet. The date of publication is October 2006. PAGE 2 | THE AUDIENCE FOR POLITICAL BLOGS INSTITUTE FOR POLITICS, DEMOCRACY & THE INTERNET down. Because of that, IPDI collaborated with the INTRODUCTION political consulting fi rm @dvocacy Inc. in an online survey that sampled a large state (California) in or- Political blogs have barnstormed into Ameri- der to reach as many dedicated political blog read- can politics.
    [Show full text]
  • Podcasting As Public Media: the Future of U.S
    International Journal of Communication 14(2020), 1683–1704 1932–8036/20200005 Podcasting as Public Media: The Future of U.S. News, Public Affairs, and Educational Podcasts PATRICIA AUFDERHEIDE American University, USA DAVID LIEBERMAN The New School, USA ATIKA ALKHALLOUF American University, USA JIJI MAJIRI UGBOMA The New School, USA This article identifies a U.S.-based podcasting ecology as public media and then examines the threats to its future. It first identifies characteristics of a set of podcasts in the United States that allow them to be usefully described as public podcasting. Second, it looks at current business trends in podcasting as platformization proceeds. Third, it identifies threats to public podcasting’s current business practices. Finally, it analyzes responses within public podcasting to the potential threats. The article concludes that currently, the public podcast ecology in the United States maintains some immunity from the most immediate threats, but there are also underappreciated threats to it, both internally and externally. Keywords: podcasting, public media, platformization, business trends, public podcasting ecology As U.S. podcasting becomes a commercially viable part of the media landscape, are its public service functions at risk? This article explores that question, in the process postulating that the concept of public podcasting has utility in describing not only a range of podcasting practices, but also an ecology within the larger podcasting ecology—one that permits analysis of both business methods and social practices, and one that deserves attention and even protection. This analysis contributes to the burgeoning literature on Patricia Aufderheide: [email protected] David Lieberman: [email protected] Atika Alkhallouf: [email protected] Jiji Majiri Ugboma: [email protected] Date submitted: 2019‒09‒27 Copyright © 2020 (Patricia Aufderheide, David Lieberman, Atika Alkhallouf, and Jiji Majiri Ugboma).
    [Show full text]
  • Seeing Destinations Through Vlogs: Implications for Leveraging Customer Engagement Behavior to Increase Travel Intention
    University of Central Florida STARS Faculty Scholarship and Creative Works 10-1-2020 Seeing Destinations Through Vlogs: Implications for Leveraging Customer Engagement Behavior to Increase Travel Intention Yusi Cheng University of Central Florida, [email protected] Wei Wei University of Central Florida, [email protected] Lu Zhang Part of the Hospitality Administration and Management Commons, and the Tourism and Travel Commons Find similar works at: https://stars.library.ucf.edu/ucfscholar University of Central Florida Libraries http://library.ucf.edu This Paper is brought to you for free and open access by STARS. It has been accepted for inclusion in Faculty Scholarship and Creative Works by an authorized administrator of STARS. For more information, please contact [email protected]. Original Citation Cheng, Y., Wei, W., & Zhang, L. (2020). Seeing destinations through vlogs: implications for leveraging customer engagement behavior to increase travel intention. International Journal of Contemporary Hospitality Management, 32(10), 3227–3248. https://doi.org/10.1108/IJCHM-04-2020-0319 Cheng, Y., Wei, W., & Zhang, L. (2020). Seeing destinations through vlogs: implications for leveraging customer engagement behavior to increase travel intention. International Journal of Contemporary Hospitality Management, 32(10), 3227-3248. Customer Engagement Behavior in Travel Vlogs: Drivers and Consequence Abstract Purpose – This research aims to understand consumers’ watching experience with travel vlogs as well as its impacts on customer engagement behavior (CEB) and travel intention. Drawing upon Theory of Resonance, this research incorporated both cognitive and emotional aspects of travel vlog watching experience. Design/methodology/approach – This study employed multiple linear regression analysis. Data were collected from 352 participants who have watched travel vlogs over the past 12 months.
    [Show full text]
  • What's Podcasting to You? Exploring Perspectives of Consumers and Producers
    What's Podcasting to you? Exploring Perspectives of Consumers and Producers Student Name - Arshdeep Chawla Module - COMM5600: Dissertation & Research Methods Course - MA New Media Submitted on - 3 September 2018 Page !1 of !79 TABLE OF CONTENTS Introduction 4 Chapter I - Literature Review 6 Podcasting 6 Overview: Podcasting Industry 7 Overview: Podcast Production 11 Experimental Application Perpective 16 Emerging Technologies - Redefining Podcast Discovery? 17 Pivotal Shows and Trends 21 Chapter II - Methodology 23 Interview 24 Chapter III - Findings, Discussions and Analysis 29 Podcasting 29 Software 33 Smart Speakers 34 Production, Distribution and Technology 36 Closing Remarks 41 Chapter IV - Conclusion 42 List of References 45 Appendices 54 Appendix I - Transcripts 54 Appendix II - Ethics Form 76 Appendix III - Research Checklist 77 Appendix IV - Information Sheet 78 Page !2 of !79 Abstract Past research has widely investigated podcasting in academia and education. Some research has investigated motivations of podcasters and listeners using quantitive methods. However, little is known about perspectives of podcast users and producers with respect to technological and cultural changes in the medium. This dissertation outlines findings from interviews conducted with podcast users and a podcast producer that lays out thoughts about the medium on themes like technology, production, distribution etc. Page !3 of !79 Introduction Podcasting, an automated subscription-based system of recorded audio/video content powered by the internet, finds its origins in the early 2000s and witnessed wide adoption in 2005. This makes podcasting older than Facebook or Twitter, two very popular products of the internet age. Although, podcasting has not been able to replicate the same success as those social networking sites, it has had a few pivotal moments that left an indelible impact on the digital media industry.
    [Show full text]
  • New York City, the Podcasting Capital
    NEW YORK CITY, THE PODCASTING CAPITAL TABLE OF CONTENTS 3 EXECUTIVE SUMMARY 7 INTRODUCTION 9 A BRIEF HISTORY OF THE PODCAST 11 NATIONAL LANDSCAPE OF PODCASTING 12 PODCAST GROWTH 14 ADVERTISING 15 THE IMPACT OF PODCAST ADVERTISING 16 ADVERTISING MODELS IN PODCASTING 17 PRICING MODEL 18 ADVERTISING TECHNOLOGY 19 NEW YORK CITY, THE CAPITAL OF PODCASTING 20 NEW YORK CITY’S PODCAST NETWORKS 22 NEW YORK CITY PODCAST INDUSTRY GROWTH 23 THE NEW YORK CITY PODCAST COMMUNITY 24 INCREASING DIVERSITY IN NEW YORK CITY PODCASTING 26 TECHNOLOGY 28 THE FUTURE OF PODCASTING 30 CONCLUSION 31 PODCASTERS’ FAVORITE PODCASTS 32 REFERENCES 33 ACKNOWLEDGEMENTS EXECUTIVE SUMMARY Podcasts are the newest form of the oldest entertainment medium: storytelling. Today’s podcasts are a major forum for the exchange of ideas, and many are calling this time the “renaissance of podcasting.” Born out of the marriage of public radio and the internet, podcasting has adapted to follow modern consumption patterns and the high demand for readily accessible entertainment. Podcasts are making New York City their home. The density of advertising firms, technology companies, major brands, digital media organizations, and talent has established New York City as the epicenter of the burgeoning podcast industry. New York City is home to the fastest growing podcast startups, which have doubled, tripled, and quadrupled their size in the past several years – in employment, office space, and listenership. New York City’s podcast networks are growing rapidly, reflecting the huge national audience of 42 million weekly listeners. Employment at the top New York City podcast networks has increased over the past several years, from about 450 people in 2015 to about 600 people in early 2017.
    [Show full text]
  • Building Your Tweet Cred a How–To Guide for Nonprofits
    Building Your Tweet Cred A How–To Guide For Nonprofits Twitter doesn’t have to be scary. With over 300 million monthly users, Twitter has quickly become the platform of choice for many nonprofits seeking to reach their followers. By creating a well-designed Twitter account, organizations can tell their story, engage communities, enlarge their volunteer base, acquire donors, and keep their supporters up to speed on the latest events and campaigns. This post will outline how to 1) set up your profile, 2) develop a strategy, 3) produce quality content 4) maximize your audience and impact, and 5) track and monitor your results. Part 1: Set Up Your Profile A magnet for first impressions, your Twitter profile will be one of the most visible descriptions of your organization on the Internet. So you have to make it count. Step 1: Create a Twitter and fill out your profile entirely. An estimated 5% of Twitter profiles are fake, and oftentimes they are easy to spot. No profile picture, no bio, and few to no followers. As you’re creating an account, think of your profile as your first chance to make an impression on a potential follower, and make sure you give them a good reason to start following along. Don’t leave your profile picture looking like this. Step 2: Write your Twitter bio. After you’ve created an account with an identifiable handle (e.g. @SkollFoundation), it’s time to write your bio. The New York Times has called the Twitter bio a “postmodern art form.” In only 160 characters, you must communicate your organization’s mission, incorporate relevant keywords, mention its location, and include a link to your website or blog, all the while being intriguing, accurate, upbeat, and irresistibly charming.
    [Show full text]
  • News Podcasts and the Opportunities for Publishers
    DIGITAL NEWS PROJECT DECEMBER 2019 News Podcasts and the Opportunities for Publishers Nic Newman and Nathan Gallo Contents About the Authors 4 Acknowledgements 4 1. Introduction 5 2. Methodology and Defi nitions 8 3. Comparing the Production of News Podcasts across Five Countries 10 4. Deep Dive into Daily News Podcasts 18 5. Wider Publisher Strategies in Detail – Case Studies 27 6. Future Developments and the Potential Impact for Publishers 34 7. Conclusions 40 Appendix A: List of Interviewees 42 Appendix B: List of Daily News Podcasts 44 THE REUTERS INSTITUTE FOR THE STUDY OF JOURNALISM About the Authors Nic Newman is Senior Research Associate at the Reuters Institute . He is lead author of the Digital News Report and an annual study looking at trends in technology and journalism. He is also a consultant on digital media, working actively with news companies on product, audience, and business strategies for digital transition. Nathan Gallo is a research assistant and journalist. He graduated from City, University of London with a Masters in Journalism, Media, and Globalisation and from Paris 1 Panthéon-Sorbonne with a Masters in Media History. Acknowledgements The authors are particularly grateful to the media executives and other experts who gave their time to be interviewed for this report. We would like, in particular, to thank Chartable for providing data on the leading news podcasts and helping to analyse news’ role in the wider podcast eco- system. Special thanks also to publishers including Les Echos, the Guardian, and The Economist for providing private industry data to illustrate specific points and allowing us to publish these.
    [Show full text]
  • Downloadable
    San FranciSco BaY arEa LOCAL PuBLic radio Program Schedule 91.7 Fm · kaLw.org Summer/Fall 2020 Studio: 415-841-4134 MONDAY TUESDAY WEDNESDAY THURSDAY FRIDAY SATURDAY SUNDAY BBC World Service 12am - 5am For detailed listings, visit bbc.co.uk/worldservice PRX Remix 5am NPR’s Morning Edition Counterspin 6am BBC Newscast live from London on the hour; Local News Update at 7:31 and 8:31; Daily Almanac at 5:49 and 8:49; TUC Radio School Lunch Menu and Updates at 6:49; Crosscurrents Morning Report at 6:51 and 8:51, Monday to Thursday; NPR’s Sandip Roy’s Dispatch from Kolkata at 7:44 on Wednesday; On Being 7am Weekend Edition Sights & Sounds at 7:44 on Thursday. 8am Hidden Brain Wait Wait… Fresh Air (with BirdNote at 9:04) 9am Don’t Tell Me! To The Best Of L L Our Knowledge Your Call, with Rose Aguilar Your Call 10am It’s Been a Minute 415-841-4134 or 866-798-TALK · [email protected] · @yourcallradio on Twitter Media Roundtable 1A 11am Podcast Playlist Philosophy Talk 855-236-1212 · [email protected] · @1A on Twitter L 12pm BBC Newshour Bullseye Le Show R R L The This Open Air, New Yorker Hidden Brain Latino USA The Splendid Table Freakonomics 1pm American Life w/ David Latulippe Radio Hour L R All Songs In Deep, Binah, Considered Reveal Big Picture Science BBC Fifth Floor Radiolab 2pm with Angie Coiro from the JCCSF Alt. Latino L 3pm Snap Judgement NPR’s All Things Considered Folk Music & Beyond, BBC Newscast live from London at 4:01; Sandip Roy’s Dispatch from Kolkata with JoAnn Mar at 4:45 on Wednesday; Sights & Sounds at 4:45 on Thursday.
    [Show full text]
  • NYT Podcast Guidelines and Best Practices
    Podcast Ads Guidelines & Best Practices The New York Times’s audio team sits in the heart of the newsroom, providing access to more amazing stories, and more reporters and critics with deep expertise, than anyone else in the podcast space. That’s what powers The Daily every day. It comes through when listening to Wesley Morris and Jenna Wortham talk about culture on Still Processing, and when Pamela Paul interviews best-selling authors on The Book Review. The success of The New York Times’ podcast suite has extended our reach and allowed us to build deeper relationships with our listeners. We’re taking what works for our editorial content and bringing it to brands. Overview Work With Us Your brand has the opportunity There are a multitude of ways your creative can come to life in a New York Times to share your story in one or podcast. T Brand Studio can help determine the best path forward for your brand. more NYT podcasts in the breaks within the podcast TIER 1 TIER 2 TIER 3 episode. Each ad spot is • Client provides up • T Brand provides • T Brand creates custom ad recorded by a voice actor and is to 2 scripts (90 script writing spots with sound design, music, mixed by T Brand Studio. words each max) assistance and premium voice talent Ad Positions Pre-Roll Mid-Roll Post-Roll Recommendation Recommendation Recommendation • Grab the listener’s attention • Customize the copy based on the • Include a call to action with a catchy opening style and tone of the podcast Deliverables Deadlines • Copy is due 15-20 days prior to the Two (2) script recordings are included in each sponsorship package.
    [Show full text]
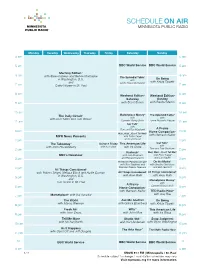
  • Schedule on Air Minnesota Public Radio
    SCHEDULE ON AIR MINNESOTA PUBLIC RADIO Monday Tuesday Wednesday Thursday Friday Saturday Sunday 4 am 4 am 5 am BBC World Service BBC World Service 5 am Morning Edition® 6 am 6 am with Steve Inskeep and Renée Montagne The Splendid Table® On Being in Washington, D.C. with and Lynne Rossetto Kasper with Krista Tippett 7 am Cathy Wurzer in St. Paul 7 am 8 am 8 am Weekend Edition® Weekend Edition® Saturday Sunday 9 am with Scott Simon with Rachel Martin 9 am 10 am 10 am ® ® The Daily Circuit™ Marketplace Money The Splendid Table with Kerri Miller and Tom Weber with with 11 am Carmen Wong Ulrich Lynne Rossetto Kasper 11 am Car Talk® with Tom and Ray Magliozzi A Prairie noon ® noon ® Home Companion Wait, Wait ... Don’t Tell Me! with Garrison Keillor MPR News Presents with Peter Sagal 1 pm and Carl Kasell 1 pm ® The Takeaway™ Science Friday This American Life Car Talk with John Hockenberry with Ira Flatow with Ira Glass with 2 pm Tom and Ray Magliozzi 2 pm Radiolab® Wait, Wait ... Don’t Tell Me!® BBC’s Newshour with Jad Abumrad with Peter Sagal 3 pm and Robert Krulwich and Carl Kasell 3 pm The Dinner Party Download™ On the Media® with Rico Gagliano and with Brooke Gladstone 4 pm Brendan Francis Newnam and Bob Garfield 4 pm All Things Considered® with Robert Siegel, Melissa Block and Audie Cornish All Things Considered® All Things Considered® with Arun Rath with Arun Rath 5 pm in Washington, D.C. 5 pm and Marketplace Money® Tom Crann in St.
    [Show full text]
  • New York Times Launches Daily Podcast Show 30 January 2017
    New York Times launches daily podcast show 30 January 2017 Last week The Washington Post launched the podcast "Can He Do That?" to assess the Trump's presidency, currently top in the US podcast charts. The Wall Street Journal also offers readers a variety of podcasts. "Our readers have always turned to us first thing in the morning to help them understand the world," said Dean Baquet, executive editor of the Times. "Now, with our new audio report, we're able to explain the news in a whole new way," he added. Last year the Times launched four new podcasts— "The Run-Up," a politics show also hosted by The New York Times plans a new daily podcast hosted Barbaro, "Modern Love," "Still Processing" and by Michael Barbaro "Tell Me Something I Don't Know." © 2017 AFP Best known for its print coverage, The New York Times is this week broadening into the realm of daily audio news by launching a brand new podcast. "The Daily," a 15-20 minute audio offering, will launch Wednesday and be available to listeners through the newspaper's website and mobile apps. The show will cover a range of topics from hard news to other topics "highlighting culturally relevant news of the day," the newspaper said. Host will be Michael Barbaro, who covered the 2016 US election and who will also share context, analysis and thoughts with Times readers by text message. The move sees the newspaper try to hold its own in a competitive news market where demand for coverage spiked during and since last year's election that ended in a shock victory for President Donald Trump.
    [Show full text]