Rockfall Stabilisation of a Steep and High Slope at West Angelas Mine Using Pre-Tensioned Anchored Mesh
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mining Robotics”
Springer Handbook of Robotics (2nd Edition) Chapter on “Mining Robotics” Joshua Marshall Queen’s University Mining Systems Laboratory Kingston, ON K7L 3N6, Canada e-mail: [email protected] Adrian Bonchis CSIRO ICT Centre 1 Technology Court Pullenvale QLD 4069, Australia e-mail: [email protected] Eduardo Nebot The University of Sydney Australian Centre for Field Robotics Sydney NSW 2006, Australia e-mail: [email protected] Steve Scheding The University of Sydney Australian Centre for Field Robotics Sydney NSW 2006, Australia e-mail: [email protected] Revised on May 9, 2014 Contents 1 Mining Robotics 3 1.1 Modern Mining Practice . .3 1.1.1 Stages of Mining . .4 1.1.2 Technology Drivers in Mining . .5 1.2 Surface Mining . .8 1.2.1 Automated Haulage . .8 1.2.2 Fleet Management . 11 1.2.3 Robotic Digging . 13 1.2.4 Robotic Dozing . 15 1.2.5 Autonomous Blasthole Drilling . 16 1.2.6 Telerobotic Rock Breaking . 17 1.2.7 Automated Loading Unit and Truck Interactions . 18 1.2.8 Dragline Automation . 22 1.2.9 Machine Positioning and Terrain Mapping . 23 1.2.10 Mine Safety . 25 1.3 Underground Mining . 29 1.3.1 Telerobotic Operations . 29 1.3.2 Autonomous Tramming . 29 1.3.3 Robotic Loading . 32 1.3.4 Longwall Automation . 35 1.3.5 Robotic Explosives Loading . 37 1.3.6 Underground Mapping, Surveying, and Positioning . 39 1.4 Challenges, Outlook, and Conclusion . 42 1.4.1 Technical Challenges . 42 1.4.2 Socio-Economic Challenges . -

Strategy Delivery Growth
Rio Tinto 2009 Annual report Rio Tinto Financial calendar Strategy 2010 14 January Fourth quarter 2009 operations review 11 February Announcement of results for 2009 24 February Rio Tinto plc and Rio Tinto Limited shares and Rio Tinto plc ADRs quoted “ex-dividend” for 2009 fi nal dividend Delivery 26 February Record date for 2009 fi nal dividend for Rio Tinto plc shares and ADRs 2 March Record date for 2009 fi nal dividend for Rio Tinto Limited shares 11 March Plan notice date for election under the dividend reinvestment plan for the 2009 fi nal dividend 1 April Payment date for 2009 fi nal dividend to holders of Ordinary shares and ADRs Growth 15 April Annual general meeting for Rio Tinto plc 15 April First quarter 2010 operations review 22 April Annual general meeting for Rio Tinto Limited A focused and 14 July Second quarter 2010 operations review 5 August Announcement of half year results for 2010 integrated strategy 11 August Rio Tinto plc and Rio Tinto Limited shares and Rio Tinto plc ADRs quoted “ex-dividend” for 2010 interim dividend 13 August Record date for 2010 interim dividend for Rio Tinto plc shares and ADRs 17 August Record date for 2010 interim dividend for Rio Tinto Limited shares Excellence in 18 August Plan notice date for election under the dividend reinvestment plan for the 2010 interim dividend 9 September Payment date for 2010 interim dividend to holders of Ordinary shares and ADRs operational delivery 14 October Third quarter 2010 operations review 2011 Positioned for growth January Fourth quarter 2010 operations review February Announcement of results for 2010 Useful information and contacts Registered offi ces Investor Centre Rio Tinto Limited Rio Tinto plc To fi nd out more about Investor Centre, go to Computershare Investor Services Pty Limited 2 Eastbourne Terrace www.investorcentre.co.uk/riotinto GPO Box 2975 London Holders of Rio Tinto American Melbourne W2 6LG Depositary Receipts (ADRs) Victoria 3001 Registered in England No. -
Mesa H Environmental Review Document Part 13.Pdf
400,000 mE 450,000 mE LEGEND y y y y aaa www hhhwww Development Envelope ggghhh iiiiiigigg HHH 22 22 Rio Tinto Ghost Bat records WARRAMBOOWARRAMBOO PP lllllll PPaannnn ttttaaa 22 nnnnaawwoo 22 OUTSTATIONOUTSTATION ssstttt RRR wwoonniiiiccc WWW aaasss iiiciccaa Ghost Bat Roost (Diurnal/ WWW oooaaa oooo 22aa (( PannawonicaPannawonica 22 22 ooo bbbb 22 88 (( PannawonicaPannawonica 22 aaaa CC bbbb 2288 aaaa !! CC e e e e 22 potential maternal) rrrrrrr !! 22 rrrrrrr aaaa mmm 2222222 RR mmm 22 22222222222 RRooo bbbb 22 22 ooo 88 8888 mN 7,600,000 bbbb aaa 2288 22882288 oooo t t t t t t t 222 ddd 22 88 DBCA Ghost Bat records o o o o t t t t t t t 222 ddd o o o o ssss 22 RRiiii 88 88 eeee RRiiiivv2v28e8e 28288 eeee MesaMesa A A 22 88 eerrrr 22828 2288 WW 22 2288 2288 2288 2288 88 22 2222 22 22 222288 Rio Tinto Railway 222288 22 22 2288 7,600,000 mN 7,600,000 222 22 22 22 Highway 2222288822 22222 22222282822 2222 28288 222 22828 Major Road h h h h ttttth tth h h rrrrrrr 22 oooo 22MesaMesa J J NNN 2222 Major Watercourse 22 22222 JJJ JJJiiimimmm MMMMMMM mm MMMMMMM mm MMMMMMM mmaa MMMMMMM aa MMMMMMM aa MMMMMMM aaww 22 wwuurrrrrrrraa Data sourced from: Department of Biodiversity, uuuuuuu rrrraa uuuuuuu aadd uuuuuuu 88 aadd uuuuuuu 88 aadd uuuuuuu 88 22 dd uuuuuuu 88 22 ddaa uuuuuuu 2288 22 ddaa nnnnnnn 22 nnnnnnn nnnnnnn CCCCCCC CCCCCCC Conservation and Attractions (2018) Threatened CCCCCCC ggggggg ggggggg ggggggg rrrrrrr rrrrrrr rrrrrrr aaaaaaa aaaaaaa eeeeeee aaaaaaa eeeeeee and Priority Fauna. -

Robe Valley Mesa B/C/H West Angelas Deposit C/D Mine Development
Robe River JV Robe Valley Mesa B/C/H West Angelas Deposit C/D Mine Development 10th October 2018 Mitsui & Co., Ltd. Agenda 1. Major Projects & Partners in Mitsui & Co.’s Mineral & Metal Resource Business 2. Summary of Mine Development Project 3. Key Project Concepts 4. Our Strategy for Iron Ore Business 2 1. Major Projects & Partners Vale Robe River (Australia) - Robe Valley Iron Ore Mine Rio Tinto - West Angelas Iron Ore Mine Mitsui & Co., Ltd. Mitsui & Co., Mt. Newman / Yandi / Goldsworthy / Jimblebar (Australia) NSSMC Iron Ore - Mt. Newman Iron Ore Mine - Yandi Iron Ore Mine Coal - Area C Iron Ore Mine - South Flank Iron Ore Mine BHP - Jimblebar Iron Ore Mine Cooper South Walker Creek / Poitrel (Australia) Moranbah North / Capcoal / Dawson Anglo American (Australia) Moatize / Nacala (Mozambique) Glencore Kestrel (Australia) Collahuasi (Chile) Codelco Anglo American Sur (AAS) (Chile) Caserones (Chile) Pan Pacific Copper 3 2. Summary of Mine Development Project Robe River JV (Rio Tinto 53%, Mitsui 33%, NSSMC 14%) will invest a total of USD 1,546 Mil. (Mitsui’s share: USD 510 Mil., equivalent to around JPY 56.1 Bil.) to develop new iron ore deposits in the Robe Valley mine and West Angelas mine in Western Australia. ① Robe Valley Mine: Mesa B/C/H Development Owner: Robe River JV Annual Production: 31 Mtpa (2017) Operating Deposits: Mesa A, Warramboo, Mesa J New Deposits: Mesa B, Mesa C, Mesa H CAPEX (Mitsui): USD319 Mil. (Approx. JPY35.1 Bil.) Commissioning: 2021 Mesa B/C xx/202x ② West Angelas Mine: Deposit C/D Development Owner: Robe River JV Annual Production: 34 Mtpa (2017) Operating Deposits: Deposit A, Deposit B, Deposit F New Deposits: Deposit C, Deposit D CAPEX (Mitsui) USD191 Mil. -

Investment in the Robe River J/V Mine Development in Western Australia
Mitsui & Co., Ltd. Investment in The Robe River J/V Mine Development in Western Australia Conference Call Q&A Session 1. Date/time: October 10, 2018 (Wed), 13:30-14:30 2. Mitsui & Co. presenters: GM of Iron Ore Div. Makoto Sato GM of Australia Business Dept. Takayuki Tsuchida GM of IR Div. Yuji Mano 3. Questions & Answers: Question 1 While this project aims to sustain iron ore production capacity, the presentation is showing an increase of equity base production until FY2020/3. What will be the production trend after FY2020/3? The Robe River J/V’s iron ore is of lower grade. Given the situation that the price differential between high and low grade iron ore is widening, are any countermeasures being taken for that? Answer 1 Our partners have not made any announcement to change their production level substantially in the near future. Thus, we do not expect any substantial changes in our production volume after FY2020/3. The Robe River J/V currently operates two mines, the Robe Valley Mine and the West Angelas Mine. The Fe grade of the former’s ore is around 57%. The latter’s ore has been blended with other iron ores from Rio Tinto’s various mines, and been sold as “Pilbara Blend” whose Fe grade is around 62%. Although Fe grade of Robe Valley’s ore is not so high, its phosphorus, which induces brittleness in steel products, is considerably low, and therefore steel mills in Japan and other countries highly appreciate this ore because it can reduce costs for dephosphorization treatment process. -

NSSMC and Mitsui to Invest in Robe River J/V Mine Development in Western Australia
October 1st, 2018 Nippon Steel & Sumitomo Metal Corporation Mitsui & Co., Ltd. NSSMC and Mitsui to Invest in Robe River J/V Mine Development in Western Australia Nippon Steel & Sumitomo Metal Corporation (“NSSMC”, Representative Director and President: Kosei Shindo) and Mitsui & Co., Ltd. (“Mitsui”, President and CEO: Tatsuo Yasunaga) are pleased to announce that Robe River Iron Associates (“Robe River J/V”, Rio Tinto 53%, Mitsui 33%, NSSMC 14%) has decided to invest in the development of new iron ore deposits, namely, the Mesa B/C/H in the Robe Valley mine and the Deposit C/D in the West Angelas mine in the Pilbara region of Western Australia. The existing deposits in both Robe Valley mine and West Angelas mine, currently in operation, are nearing the end of their lifespan. The Robe River J/V will develop these new deposits utilizing the existing rail and port infrastructure, with the objective of sustaining current rates of iron ore production as existing mines decline. Subject to government and environmental approvals, development of new deposits is expected to start next year, and first ore is currently anticipated from 2021. The total investment in the subject development is estimated to be US$1,546 million (equivalent to approximately 170.1 billion yen), of which NSSMC and Mitsui will invest US$216 million (approximately 23.8 billion yen) and US$510 million (approximately 56.1 billion yen) , respectively, in proportion to each of their equity stakes. NSSMC and Mitsui will work together with Rio Tinto through the Robe River J/V to stably procure and supply iron ore, for which further demand is expected. -

Mesa H Proposal Title
Referral of proposed action Proposed action Mesa H Proposal title: 1. Summary of proposed action Short description: Robe River Mining Co. Pty. Limited (the Proponent), as manager and agent for the Robe River Iron Associates joint venture (RRIA), is seeking to extend the existing Mesa J operations by developing the adjacent iron ore deposit at Mesa H. The Mesa H Proposal is 1.1 located approximately 16 km south west of Pannawonica in the Pilbara region of Western Australia (refer Attachment 1). This Proposed Action will involve development of additional mine pits, mineral waste dumps and associated infrastructure, processing facilities and water management infrastructure to sustain the Robe Valley Operations ore feed at 35 Mt/annum. Latitude and longitude 1.2 Nodes are provided in Table 1 below. Table 1: Nodes for the area subject to the Proposed Action Location Latitude Longitude point degrees minutes seconds degrees minutes seconds 1 -21 42 20.68 116 10 53.24 2 -21 42 20.68 116 13 5.45 3 -21 42 20.45 116 13 35.63 4 -21 42 20.53 116 13 35.63 5 -21 42 20.80 116 14 7.07 6 -21 42 44.29 116 14 6.94 7 -21 42 46.58 116 14 1.26 8 -21 43 3.19 116 13 51.90 9 -21 43 19.00 116 13 59.56 10 -21 43 48.73 116 13 59.17 11 -21 43 58.08 116 14 6.22 12 -21 44 1.24 116 14 1.76 13 -21 44 0.76 116 13 59.28 14 -21 43 57.50 116 13 58.17 15 -21 43 56.47 116 13 50.38 16 -21 43 54.13 116 13 47.10 17 -21 43 45.98 116 13 45.93 18 -21 43 45.72 116 13 35.20 19 -21 45 12.57 116 13 35.09 20 -21 45 12.58 116 13 15.15 21 -21 45 51.61 116 13 14.94 22 -21 45 51.70 116 13 -

West Angelas Closure Plan April 2018
Robe River Mining Co. Pty Ltd ABN: 71 008 694 246 West Angelas Closure Plan April 2018 Mineral Field 47 – West Pilbara FDMS No RTIO-HSE-0228290 Contact details: Nina McEwan Rio Tinto’s iron ore group Central Park 152 – 158 St Georges Terrace, Perth Perth, WA 6837 T: +61 8 9217 3009 E: [email protected] http://www.riotinto.com West Angelas Closure Plan April 2018 EXECUTIVE SUMMARY Overview West Angelas is an open cut iron ore mine located in the Eastern Pilbara region of Western Australia, approximately 105 km north-west of Newman. The mine uses conventional drill-and-blast and load-and-haul mining methods to remove iron ore from above and below the water table. Scope This closure plan covers currently approved deposits and associated infrastructure at West Angelas (Deposits A, A West, B, E and F) and the proposed C, D and G deposits that have been referred to the Environmental Protection Authority (EPA) for environmental approval. It is an update of the February 2015 version of the West Angelas closure plan, and will supersede that document once it has been formally accepted. The closure plan has been developed to meet the requirements of the Rio Tinto Closure Standard and the joint Department of Mines and Petroleum (DMP) and EPA Guidelines for Preparing Mine Closure Plans (May 2015). Post-mining land use As West Angelas is underlain by Vacant Crown Land, and is located in close proximity to Karijini National Park, the return of a native ecosystem is considered to be the most appropriate final land use. -

Adventures in Automation
INSIDE Big Data insights from IBM Barrick’s processing innovation Drones take flight FALL 2015 ADVENTURES IN AUTOMATION Complimentary PM# 40069240 MTD Cover.indd 1 2015-10-30 3:02 PM GET ON BOARD WITH A LEADING SOURCE OF MINING COMPANY & PROPERTY DATA The 2016 Canadian & American Mines Handbook is an incredibly powerful resource in your business arsenal. Featuring comprehensive pro les on over 2,000 active publicly-traded mining companies as well as over 1,400 mines and advanced projects related to those companies, your business decisions will always be backed up by the most up-to-date industry data. $136 Order Your Copy Today! + S/H Call 1-888-502-3456 or by email at [email protected] www.mineshandbook.com Canadian & American Mines Handbook - 38 Lesmill Rd., Unit 2, Toronto ON, M3B 2T5 House Ad IFC.indd 2 2015-10-30 3:03 PM FALL 2015 PUBLISHER: Anthony Vaccaro ADVERTISING SALES: Joe Crofts Dave Chauvin Michael Winter EDITOR: Alisha Hiyate ART DIRECTOR: Stephen Ferrie 8 12 PRODUCTION MANAGER: Jessica Jubb CONTRIBUTING WRITERS: Lesley Stokes Nathan Stubina PUBLISHED BY 38 Lesmill Rd, Unit 2, Toronto, Ontario, M3B 2T5 Phone: (416) 510-6768 18 20 Fax: (416) 510-5138 E-mail: [email protected] EDITORIAL CORPORATE PROFILES Printed in Canada. THE INNOVATION IMPERATIVE PAGE 15 All rights reserved. The contents of this publication may PAGE 4 only be reproduced with the written THE CUTTING EDGE consent of The Northern Miner. Issue price: $6.00 Q&A CRACKING DOUBLE-REFRACTORY ORE BIG DATA INSIGHTS FROM Barrick pioneers cyanide-free processing -

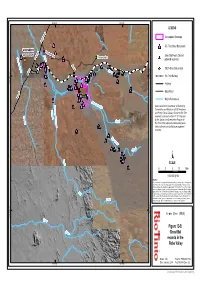
Risk Management and Remediation of the North Wall Slip, West Angelas Mine, Western Australia
Slope Stability 2013 – P.M. Dight (ed) © 2013 Australian Centre for Geomechanics, Perth, ISBN 978-0-9870937-5-2 doi:10.36487/ACG_rep/1308_69_DeGraaf Risk management and remediation of the north wall slip, West Angelas Mine, Western Australia G.G. Joass Rio Tinto Iron Ore, Australia R. Dixon Rio Tinto Iron Ore, Australia T. Sikma Rio Tinto Iron Ore, Australia S.D.N. Wessels Rio Tinto Iron Ore, Australia J. Lapwood Rio Tinto Iron Ore, Australia P.J.H. de Graaf Rio Tinto Iron Ore, Australia Abstract A planar failure of approximately 600 kT occurred on the north wall of Centre Pit North (CEPN) at West Angelas Mine site in February 2010. The failure impacted a substantial resource of high grade iron ore and left a number of significant geotechnical hazards on and adjacent to the failure surface. These presented a series of challenges which had to be overcome in order to remediate the failure and reclaim the bulk of the buried ore. A number of recovery options were investigated and presented to management. This paper outlines the plan which was adopted, the challenges encountered during its implementation and the risk management and mining procedures used to bring the remediation and recovery to a successful conclusion. 1 Introduction A significant fall of ground occurred on the north wall of CEPN at the West Angelas Mine site on the evening of the 3 February 2010. The failure occurred in the Mount Newman Member of the Marra Mamba Iron Formation, which is comprised predominantly of banded iron formation (BIF) with interbedded shale. -

Deposit a West Angelas, Western Australia
Slope Stability 2007 — Y. Potvin (ed) ©2007 Australian Centre for Geomechanics, Perth, ISBN 978-0-9756756-8-7 https://papers.acg.uwa.edu.au/p/708_31_Eggers/ Pit Slope Design in Pilbara Iron Deposits — Deposit A West Angelas, Western Australia M.J. Eggers Pells Sullivan Meynink Pty Ltd, Australia D.L. Casparis Rio Tinto Iron Ore, Australia Abstract The Deposit A pit design at West Angelas, Western Australia is characterised by a long, narrow shape which will ultimately be some six kilometres in length and up to 200 metres deep. This paper summarises geotechnical investigations undertaken to date for pit slope design, describes the notable elements of the structural and rock mass models that characterise the deposit and discusses their impacts on slope stability and design. The deposit comprises three primary synclines which are asymmetrical in shape, north-verging and open to isoclinal in attitude. The southern limbs are short, steeply dipping to overturned and contain tight second- order parasitic folds while the northern limbs are longer, planar and moderately dipping. Thrust faults are interpreted in some areas of the southern limbs to accommodate a repetition in sequence although there is some evidence this may also be due to recumbent folding. A major objective of the geotechnical studies was to investigate any differences in structural and rock mass conditions between the northern and southern limbs of the primary synclines. Several controls were investigated including lithostratigraphy, weathering and alteration related to near-surface and mineralisation effects and structural controls such as folding and faulting. A “halo” of oxidised and altered Banded Iron Formation (BIF) surrounds the mineralised zone, while there are some differences between the relatively clay-rich and clay-poor zones of the BIF units. -

IRON ORE by William S
IRON ORE By William S. Kirk Domestic survey data and tables were prepared by Jim Peang, statistical assistant, and the world production table was prepared by Linder Roberts, international data coordinator. Iron ore production in the United States rose by 12%, but from the blast furnace. A major increase in production would consumption fell to its lowest level since 1991. World iron entail restarting blast furnaces and hiring new personnel. The ore production and consumption rose in 2002. Brazil was the steel business is highly cyclical, and when demand falls, as it largest producer of iron ore in terms of iron content, and China inevitably does, the steelmakers will not have to shut down was by far the largest consumer. Iron ore trade increased and recently opened blast furnaces and lay off recently hired prices fell. Pig iron and steel production rose. personnel. So, despite increases in both steel production and Iron ore is essential to the economy and national security of demand in 2002, iron ore consumption fell to its lowest level in the United States. As the basic raw material from which iron decades. and steel are made, its supply is critical to any industrial country. Scrap is used as a supplement in steelmaking but is limited as Legislation and Government Programs a major feed material because the supply of high-quality scrap is limited. However, alternatives, such as direct reduced iron The State of Michigan passed bill 516, the Michigan Minerals (DRI), were available, and their use is growing. Credit Bill, which provides a $1-per-ton tax credit to any steel Iron ore is a mineral substance which, when heated in the company that purchases pellets from the Tilden Mine (Mining presence of a reductant, will yield metallic iron.