DOCSLIB.ORG

Maxwell's Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Maxwell's Equations Microwave Measurement and Beam Instrumentation Course at Jefferson Laboratory, January 15-26th 2018 Lecture: Maxwell’s Equations F. Marhauser Monday, January 15, 2018 This Lecture － This lecture provides theoretical basics useful for follow-up lectures on resonators and waveguides － Introduction to Maxwell’s Equations • Sources of electromagnetic fields • Differential form of Maxwell’s equation • Stokes’ and Gauss’ law to derive integral form of Maxwell’s equation • Some clarifications on all four equations • Time-varying fields wave equation • Example: Plane wave － Phase and Group Velocity － Wave impedance 2 Maxwell’s Equations A dynamical theory of the electromagnetic field James Clerk Maxwell, F. R. S. Philosophical Transactions of the Royal Society of London, 1865 155, 459-512, published 1 January 1865 Maxwell’s Equations - Originally there were 20 equations Taken from Longair, M. 2015 ‘...a paper ...I hold to be great guns’: a commentary on Maxwell (1865) ‘A dynamical theory of the electromagnetic field’. Phil. Trans. R. Soc. A 373: 20140473. Sources of Electromagnetic Fields － Electromagnetic fields arise from 2 sources: • Electrical charge (Q) Stationary charge creates electric field 푑푄 • Electrical current (퐼 = ) 푑푡 Moving charge creates magnetic field － Typically charge and current densities are utilized in Maxwell’s equations to quantify the effects of fields: 푑푄 • ρ = electric charge density – total electric charge per unit volume V 푑푉 (or 푄 = 푉 휌 푑푉) 퐼(푆) • 퐽 = lim electric current density – total electric current per unit area S 푆→0 푆 (or 퐼 = 푆 퐽 ∙ 푑푆) － If either the magnetic or electrical fields vary in time, both fields are coupled and the resulting fields follow Maxwell’s equations 5 Maxwell’s Equations Differential Form 휌 (1) 훻 ∙ 퐷 = 휌 or 훻 ∙ 퐸 = Gauss’s law 휖0 (2) 훻 ∙ 퐵 = 0 Gauss’s law for magnetism 휕퐵 (3) 훻 × 퐸 = − Faraday’s law of induction 휕푡 휕퐷 휕퐸 (4) 훻 × 퐻 = 퐽 + or 훻 × 퐵 = 휇 퐽 + 휇 휖 Ampère’s law 휕푡 0 0 0 휕푡 - Together with the Lorentz force these equations 퐹 = 푞(퐸 + v × 퐵) Lorentz Force form the basic of the classic electromagnetism ρ = electric charge density (As/m3) 퐷 = 휖 퐸 0 J = electric current density (A/m2) 휖0=permittivity of free space D = electric flux density/displacement field (Unit: As/m2) E = electric field intensity (Unit: V/m) 퐵 = 휇0퐻 H = magnetic field intensity (Unit: A/m) µ0=permeability of free space B = magnetic flux density (Unit: Tesla=Vs/m2) 6 Divergence (Gauss’) Theorem { div (훻 ∙ 퐹 ) 푑푉 = (퐹 ∙ 푛 )푑푆 = 퐹 ∙ 푑푆 푉 푆 푆 Integral of divergence of vector field (퐹 ) over volume V inside closed boundary S equals outward flux of vector field (퐹 ) through closed surface S 휕 휕 휕 휕퐹 휕퐹푦 휕퐹 훻 ∙ 퐹 = , , ∙ 퐹 , 퐹 , 퐹 = 푥 + + 푧 휕푥 휕푦 휕푧 푥 푦 푧 휕푥 휕푦 휕푧 7 Curl (Stokes’) Theorem { curl (훻 × 퐹 ) · 푑푆 = ((훻 × 퐹 ) ∙ 푛 )푑푆 = 퐹 ∙ 푑푙 푆 푆 휕푆 Integral of curl of vector field (퐹 ) over surface S equals line integral of vector field (퐹 ) over closed boundary dS defined by surface S 푖 푗 푘 휕퐹 휕퐹 휕퐹 휕퐹 휕퐹 휕퐹 훻 × 퐹 = 휕 휕 휕 = 푧 − 푦 푖 + 푥 − 푧 푗+ 푦 − 푥 푘 휕푥 휕푦 휕푧 휕푦 휕푧 휕푧 휕푥 휕푧 휕푦 퐹푥 퐹푦 퐹푧 휕퐹푦(푥, 푦) 휕퐹 (푥, 푦) 풆. 품. : 푭 = ퟎ → 훻 × 퐹 = − 푥 푘 풛 휕푥 휕푦 Curl vector is perpendicular to surface S ; 푘 = 푛 휕퐹푦(푥, 푦) 휕퐹 (푥, 푦) ( − 푥 ) 푑푆 = 퐹 푑푥 + 퐹 푑푦 Green’s Theorem 휕푥 휕푦 푥 푦 푆 휕푆 8 Example: Curl (Stokes’) Theorem curl { (훻 × 퐹 ) · 푑푆 = ((훻 × 퐹 ) ∙ 푛 )푑푆 = 퐹 ∙ 푑푙 푆 푆 휕푆 Integral of curl of vector field (퐹 ) over surface S equals line integral of vector field (퐹 ) over closed boundary dS defined by surface S 9 Example: Curl (Stokes) Theorem curl { (훻 × 퐹 ) · 푑푆 = ((훻 × 퐹 ) ∙ 푛 )푑푆 = 퐹 ∙ 푑푙 푆 푆 휕푆 Integral of curl of vector field (퐹 ) over surface S equals line integral of vector field (퐹 ) over closed boundary dS defined by surface S Example: Closed line integrals of various vector fields No curl Some curl Stronger curl No net curl 10 Maxwell’s Equations Differential Form Integral Form 훻 ∙ 퐷 = 휌 퐷 ∙ 푑푆 = 휌 푑푉 (훻 ∙ 퐹 ) 푑푉 = 퐹 ∙ 푑푆 Gauss’s law 푉 푆 푆 푉 } Gauss’ theorem 훻 ∙ 퐵 = 0 퐵 ∙ 푑푆 = 0 Gauss’s law for magnetism 푆 휕퐵 휕퐵 Faraday’s law of induction 훻 × 퐸 = − 퐸 ∙ 푑푙 = − ∙ 푑푆 휕푡 (훻 × 퐹 ) · 푑푆 = 퐹 ∙ 푑푙 휕푡 푆 휕푆 휕푆 푆 휕퐷 } Stokes’ theorem 휕퐷 Ampère’s law 훻 × 퐻 = 퐽 + 퐻 ∙ 푑푙 = 퐽 ∙ 푑푆 + ∙ 푑푆 휕푡 휕푡 휕푆 푆 푆 ρ = electric charge density (C/m3=As/m3) 퐷 = 휖0퐸 J = electric current density (A/m2) 휖0=permittivity of free space D = electric flux density/displacement field (Unit: As/m2) E = electric field intensity (Unit: V/m) 퐵 = 휇0퐻 H = magnetic field intensity (Unit: A/m) 2 µ0=permeability of free space B = magnetic flux density (Unit: Tesla=Vs/m ) 11 Electric Flux & 1st Maxwell Equation Definition of Electric Flux Gauss: Integration over closed surface 1. Uniform field 퐸 = 퐸 ∙ 푆 = 퐸 ∙ 푛 푆 = 퐸 ∙ 푆 ∙ 푐표푠 휃 [푉푚] 휖0퐸 ∙ 푑푆 = 휖0 푬 = 휌 푑푉 = 푞푖 - angle between field and normal vector 푆 푉 푖 to surface matters 푖 푞푖 ; 퐷 = 휖0퐸 퐸= 휖0 Example: Metallic plate, assume only surface charges on one side 2. Non-Uniform field 2 푑퐸 = 퐸 ∙ 푑푆 = 퐸 ∙ 푛 푑푆 휖0퐸 ∙ 푑푆 = 휖0 퐸 휋푅 = 푞푖 = 푄푐푖푟푐푙푒 푆 푖 ; 푐푟푐푙푒 푆 = 휋푅2 퐸 = 퐸 ∙ 푑푆 푄푐푖푟푐푙푒 퐸 = 2 푆 휖0휋푅 12 Electric Flux & 1st Maxwell Equation Definition of Electric Flux Gauss: Integration over closed surface 1. Uniform field 퐸 = 퐸 ∙ 푆 = 퐸 ∙ 푛 푆 = 퐸 ∙ 푆 ∙ 푐표푠 휃 [푉푚] 휖0퐸 ∙ 푑푆 = 휖0 푬 = 휌 푑푉 = 푞푖 - angle between field and normal vector 푆 푉 푖 to surface matters 푖 푞푖 ; 퐷 = 휖0퐸 퐸= 휖0 Example: Capacitor 2. Non-Uniform field 퐸 = 0 퐸 = 0 푑퐸 = 퐸 ∙ 푑푆 = 퐸 ∙ 푛 푑푆 푄푐푖푟푐푙푒 −푄푐푖푟푐푙푒 퐸= + = 0 퐸 = 퐸 ∙ 푑푆 휖0 휖0 푆 13 Electric Flux & 1st Maxwell Equation Examples of non-uniform fields Point charge Q Add charges 휖0퐸 ∙ 푑푆 = 휌 푑푉 = 푞푖 = 푄푠푝ℎ푒푟푒 푆 푉 푖 퐸 퐸 Integration of over closed spherical surface S 2 휖0퐸 ∙ 푑푆 = 휖0푬(푟)4휋푟 = 푄 푆 푞 푞 −푞 3푞 푄 ; 푠푝ℎ푒푟푒 푆 = 4휋푟2 푖 푖 푠푝ℎ푒푟푒 pointing out radially 퐸= = + = 0 퐸= = 휖0 휖0 휖0 휖0 휖0 Principle of Superposition holds: 푄 푬(푟) = ∙ 풓 2 1 푞1 푞2 푞3 휖04휋푟 퐸(푟) = 2 푟푐 1+ 2 푟푐2 + 2 푟푐3 + ⋯ 휖04휋 푟푐1 − 푟 푟푐2 − 푟 푟푐3 − 푟 14 Magnetic Flux & 2nd Maxwell Equation Definition of Magnetic Flux Gauss: Integration over closed surface Uniform field = 퐵 ∙ 푆 = 퐵 ∙ 푛 푆 = 퐵 ∙ 푆 푐표푠 휃 [푊푏 = 푉푠] 퐵 퐵 ∙ 푑푆 = 0 푀= 0 푆 - There are no magnetic monopoles - All magnetic field lines form loops 퐵 퐵 Non-Uniform field 푑퐵 = 퐵 ∙ 푑푆 = 퐵 ∙ 푛 푑푆 Closed surface: What about this case? Flux lines out = flux lines in Flux lines out > flux lines in ? = 퐵 ∙ 푑푆 퐵 - No. In violation of 2nd Maxwell’s law, i.e. 푆 integration over closed surface, no holes allowed - Also: One cannot split magnets into separate poles, i.e. there always will be a 15 North and South pole Magnetic Flux & 3rd Maxwell Equation If integration path is not changing in time 푑 푑퐵 퐸 ∙ 푑푙 = − 퐵 ∙ 푑푆 = − ; = 퐵 ∙ 푑푆 푑푡 푑푡 퐵 푆 휕푆 푆 - Change of magnetic flux induces an electric field along a closed loop - Note: Integral of electrical field over closed loop may be non-zero, when induced by a time-varying magnetic field - Electromotive force (EMF) Ɛ: 퐵(푡 = 푡1) Ɛ = 퐸 ∙ 푑푙 [푉] 휕푆 - Ɛ equivalent to energy per unit charge traveling once around loop Faraday’s law of induction 16 Magnetic Flux & 3rd Maxwell Equation If integration path is not changing in time 푑 푑퐵 퐸 ∙ 푑푙 = − 퐵 ∙ 푑푆 = − ; = 퐵 ∙ 푑푆 푑푡 푑푡 퐵 푆 휕푆 푆 - Change of magnetic flux induces an electric field along a closed loop - Note: Integral of electrical field over closed loop may be non-zero, when induced by a time-varying magnetic field - Electromotive force (EMF) Ɛ: 퐵(푡) Ɛ = 퐸 ∙ 푑푙 [푉] 휕푆 - Ɛ equivalent to energy per unit charge traveling once around loop - or voltage measured at end of open loop Faraday’s law of induction 17 Ampère's (circuital) Law or 4th Maxwell Equation Right hand side of equation: - Note that 퐽 ∙ 푑푆 is a surface integral, but S may 휕퐷 푆 퐻 ∙ 푑푙 = 퐽 ∙ 푑푆 + ∙ 푑푆 have arbitrary shape as long as ∂S is its closed 휕푡 휕푆 푆 푆 boundary { conduction current I 퐽 ∙ 푑푆 = 퐼 Example: 퐵 푆 - What if there is a capacitor? Left hand side of equation: - While current is still be flowing (charging capacitor): 퐵 ∙ 푑푙 = 푩 푟 2휋푟 = 휇0퐼 푑푄 휕푆 퐽 ∙ 푑푆 = 퐼 = tangential to a circle at any 푑푡 푆 ; 퐵 = 휇0퐻 radius r of integration ; 푐푟푐푢푚푓푒푟푒푛푐푒 퐶 = 2휋푟 휇 퐼 |푩 푟 | = 0 2휋푟 18 Ampère's (circuital) Law or 4th Maxwell Equation - But one may also place integration surface S between plates current does not flow through surface here 휕퐷 퐻 ∙ 푑푙 = 퐽 ∙ 푑푆 + ∙ 푑푆 휕푡 휕푆 푆 푆 퐽 ∙ 푑푆 = 0 { 푆 conduction current I 푤ℎ푙푒 퐵 ≠ 0 ? Example: 퐵 - This is when the displacement field is required as a corrective 2nd source term for the magnetic fields 휕퐷 푑 푑푄 푑 ∙ 푑푆 = 퐷 ∙ 푑푆 = = 퐼 = 휖 퐸 Left hand side of equation: 휕푡 푑푡 푑푡 퐷 0 푑푡 푆 푆 ; Gauss’s law { 퐵 ∙ 푑푙 = 푩 푟 2휋푟 = 휇0퐼 displacement current I 휕푆 푑퐸 tangential to a circle at any 퐻 ∙ 푑푙 = 퐼 + 휖0 ; 퐵 = 휇0퐻 radius r of integration 푑푡 휕푆 ; 푐푟푐푢푚푓푒푟푒푛푐푒 퐶 = 2휋푟 퐸 휇0퐼 |푩 푟 | = 휇 퐼 2휋푟 |푩 푟 | = 0 퐷 19 퐵 2휋푟 Presence of Resistive Material 휕퐷 퐻 ∙ 푑푙 = 퐽 ∙ 푑푆 + ∙ 푑푆 휕푡 휕푆 푆 푆 { { conduction current displacement current - In resistive materials the current density J is proportional to the electric field 1 퐽 = 퐸 = 퐸 with the electric conductivity (1/(Ω·m) or S/m), respectively 휌 =1/ the electric resistivity (Ω·m) - Generally (ω, T) is a function of frequency and temperature 20 퐵 Time-Varying E-Field in Free Space - Assume charge-free, homogeneous, linear, and isotropic medium - We can derive a wave equation: 휕퐵 훻 × 퐸 = − ;Faraday’s law of induction 휕푡 휕퐵 휕 훻 × 훻 × 퐸 = −훻 × = − 훻 × 퐵 ; || curl 휕푡 휕푡 훻2= Δ = Laplace operator 휕 휕퐷 훻 훻 ∙ 퐸 − 훻2퐸 = −휇 퐽 + ; curl of curl 훻 × 훻 × 퐴 = 훻 훻 ∙ 퐴 − 훻2퐴 휕푡 휕푡 휕퐷 ; 훻 × 퐻 = 퐽 + ; Ampère’s law 휕푡 휌 휕 휕퐸 훻 − 훻2퐸 = −휇 퐸 + 휖 휖0 휕푡 휕푡 ; Gauss’s law ; 퐽 = 퐸 휕2퐸 훻2퐸 − 휇휖 = 0 Homogeneous wave equation 휕푡2 ; we presumed no charge 21 Time-Varying B-Field in Free Space - Assume charge-free, homogeneous, linear, and isotropic
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • EM Concept Map
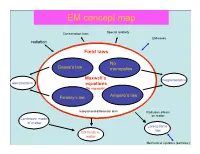
    EM concept map Conservation laws Special relativity EM waves radiation Field laws No Gauss’s law monopoles ConservationMaxwell’s laws magnetostatics electrostatics equations (In vacuum) Faraday’s law Ampere’s law Integral and differential form Radiation effects on matter Continuum model of matter Lorenz force law EM fields in matter Mechanical systems (particles) Electricity and Magnetism PHYS-350: (updated Sept. 9th, (1605-1725 Monday, Wednesday, Leacock 109) 2010) Instructor: Shaun Lovejoy, Rutherford Physics, rm. 213, local Outline: 6537, email: [email protected]. 1. Vector Analysis: Tutorials: Tuesdays 4:15pm-5:15pm, location: the “Boardroom” Algebra, differential and integral calculus, curvilinear coordinates, (the southwest corner, ground floor of Rutherford physics). Office Hours: Thursday 4-5pm (either Lhermitte or Gervais, see Dirac function, potentials. the schedule on the course site). 2. Electrostatics: Teaching assistant: Julien Lhermitte, rm. 422, local 7033, email: Definitions, basic notions, laws, divergence and curl of the electric [email protected] potential, work and energy. Gervais, Hua Long, ERP-230, [email protected] 3. Special techniques: Math background: Prerequisites: Math 222A,B (Calculus III= Laplace's equation, images, seperation of variables, multipole multivariate calculus), 223A,B (Linear algebra), expansion. Corequisites: 314A (Advanced Calculus = vector 4. Electrostatic fields in matter: calculus), 315A (Ordinary differential equations) Polarization, electric displacement, dielectrics. Primary Course Book: "Introduction to Electrodynamics" by D. 5. Magnetostatics: J. Griffiths, Prentice-Hall, (1999, third edition). Lorenz force law, Biot-Savart law, divergence and curl of B, vector Similar books: potentials. -“Electromagnetism”, G. L. Pollack, D. R. Stump, Addison and 6. Magnetostatic fields in matter: Wesley, 2002.
    [Show full text]
  • Chapter 2 Introduction to Electrostatics
    Chapter 2 Introduction to electrostatics 2.1 Coulomb and Gauss’ Laws We will restrict our discussion to the case of static electric and magnetic fields in a homogeneous, isotropic medium. In this case the electric field satisfies the two equations, Eq. 1.59a with a time independent charge density and Eq. 1.77 with a time independent magnetic flux density, D (r)= ρ (r) , (1.59a) ∇ · 0 E (r)=0. (1.77) ∇ × Because we are working with static fields in a homogeneous, isotropic medium the constituent equation is D (r)=εE (r) . (1.78) Note : D is sometimes written : (1.78b) D = ²oE + P .... SI units D = E +4πP in Gaussian units in these cases ε = [1+4πP/E] Gaussian The solution of Eq. 1.59 is 1 ρ0 (r0)(r r0) 3 D (r)= − d r0 + D0 (r) , SI units (1.79) 4π r r 3 ZZZ | − 0| with D0 (r)=0 ∇ · If we are seeking the contribution of the charge density, ρ0 (r) , to the electric displacement vector then D0 (r)=0. The given charge density generates the electric field 1 ρ0 (r0)(r r0) 3 E (r)= − d r0 SI units (1.80) 4πε r r 3 ZZZ | − 0| 18 Section 2.2 The electric or scalar potential 2.2 TheelectricorscalarpotentialFaraday’s law with static fields, Eq. 1.77, is automatically satisfied by any electric field E(r) which is given by E (r)= φ (r) (1.81) −∇ The function φ (r) is the scalar potential for the electric field. It is also possible to obtain the difference in the values of the scalar potential at two points by integrating the tangent component of the electric field along any path connecting the two points E (r) d` = φ (r) d` (1.82) − path · path ∇ · ra rb ra rb Z → Z → ∂φ(r) ∂φ(r) ∂φ(r) = dx + dy + dz path ∂x ∂y ∂z ra rb Z → · ¸ = dφ (r)=φ (rb) φ (ra) path − ra rb Z → The result obtained in Eq.
    [Show full text]
  • Electromagnetism What Is the Effect of the Number of Windings of Wire on the Strength of an Electromagnet?
    TEACHER’S GUIDE Electromagnetism What is the effect of the number of windings of wire on the strength of an electromagnet? GRADES 6–8 Physical Science INQUIRY-BASED Science Electromagnetism Physical Grade Level/ 6–8/Physical Science Content Lesson Summary In this lesson students learn how to make an electromagnet out of a battery, nail, and wire. The students explore and then explain how the number of turns of wire affects the strength of an electromagnet. Estimated Time 2, 45-minute class periods Materials D cell batteries, common nails (20D), speaker wire (18 gauge), compass, package of wire brad nails (1.0 mm x 12.7 mm or similar size), Investigation Plan, journal Secondary How Stuff Works: How Electromagnets Work Resources Jefferson Lab: What is an electromagnet? YouTube: Electromagnet - Explained YouTube: Electromagnets - How can electricity create a magnet? NGSS Connection MS-PS2-3 Ask questions about data to determine the factors that affect the strength of electric and magnetic forces. Learning Objectives • Students will frame a hypothesis to predict the strength of an electromagnet due to changes in the number of windings. • Students will collect and analyze data to determine how the number of windings affects the strength of an electromagnet. What is the effect of the number of windings of wire on the strength of an electromagnet? Electromagnetism is one of the four fundamental forces of the universe that we rely on in many ways throughout our day. Most home appliances contain electromagnets that power motors. Particle accelerators, like CERN’s Large Hadron Collider, use electromagnets to control the speed and direction of these speedy particles.
    [Show full text]
  • Electromagnetism As Quantum Physics
    Electromagnetism as Quantum Physics Charles T. Sebens California Institute of Technology May 29, 2019 arXiv v.3 The published version of this paper appears in Foundations of Physics, 49(4) (2019), 365-389. https://doi.org/10.1007/s10701-019-00253-3 Abstract One can interpret the Dirac equation either as giving the dynamics for a classical field or a quantum wave function. Here I examine whether Maxwell's equations, which are standardly interpreted as giving the dynamics for the classical electromagnetic field, can alternatively be interpreted as giving the dynamics for the photon's quantum wave function. I explain why this quantum interpretation would only be viable if the electromagnetic field were sufficiently weak, then motivate a particular approach to introducing a wave function for the photon (following Good, 1957). This wave function ultimately turns out to be unsatisfactory because the probabilities derived from it do not always transform properly under Lorentz transformations. The fact that such a quantum interpretation of Maxwell's equations is unsatisfactory suggests that the electromagnetic field is more fundamental than the photon. Contents 1 Introduction2 arXiv:1902.01930v3 [quant-ph] 29 May 2019 2 The Weber Vector5 3 The Electromagnetic Field of a Single Photon7 4 The Photon Wave Function 11 5 Lorentz Transformations 14 6 Conclusion 22 1 1 Introduction Electromagnetism was a theory ahead of its time. It held within it the seeds of special relativity. Einstein discovered the special theory of relativity by studying the laws of electromagnetism, laws which were already relativistic.1 There are hints that electromagnetism may also have held within it the seeds of quantum mechanics, though quantum mechanics was not discovered by cultivating those seeds.
    [Show full text]
  • The Lorentz Force
    CLASSICAL CONCEPT REVIEW 14 The Lorentz Force We can find empirically that a particle with mass m and electric charge q in an elec- tric field E experiences a force FE given by FE = q E LF-1 It is apparent from Equation LF-1 that, if q is a positive charge (e.g., a proton), FE is parallel to, that is, in the direction of E and if q is a negative charge (e.g., an electron), FE is antiparallel to, that is, opposite to the direction of E (see Figure LF-1). A posi- tive charge moving parallel to E or a negative charge moving antiparallel to E is, in the absence of other forces of significance, accelerated according to Newton’s second law: q F q E m a a E LF-2 E = = 1 = m Equation LF-2 is, of course, not relativistically correct. The relativistically correct force is given by d g mu u2 -3 2 du u2 -3 2 FE = q E = = m 1 - = m 1 - a LF-3 dt c2 > dt c2 > 1 2 a b a b 3 Classically, for example, suppose a proton initially moving at v0 = 10 m s enters a region of uniform electric field of magnitude E = 500 V m antiparallel to the direction of E (see Figure LF-2a). How far does it travel before coming (instanta> - neously) to rest? From Equation LF-2 the acceleration slowing the proton> is q 1.60 * 10-19 C 500 V m a = - E = - = -4.79 * 1010 m s2 m 1.67 * 10-27 kg 1 2 1 > 2 E > The distance Dx traveled by the proton until it comes to rest with vf 0 is given by FE • –q +q • FE 2 2 3 2 vf - v0 0 - 10 m s Dx = = 2a 2 4.79 1010 m s2 - 1* > 2 1 > 2 Dx 1.04 10-5 m 1.04 10-3 cm Ϸ 0.01 mm = * = * LF-1 A positively charged particle in an electric field experiences a If the same proton is injected into the field perpendicular to E (or at some angle force in the direction of the field.
    [Show full text]
  • Gauss' Linking Number Revisited
    October 18, 2011 9:17 WSPC/S0218-2165 134-JKTR S0218216511009261 Journal of Knot Theory and Its Ramifications Vol. 20, No. 10 (2011) 1325–1343 c World Scientific Publishing Company DOI: 10.1142/S0218216511009261 GAUSS’ LINKING NUMBER REVISITED RENZO L. RICCA∗ Department of Mathematics and Applications, University of Milano-Bicocca, Via Cozzi 53, 20125 Milano, Italy [email protected] BERNARDO NIPOTI Department of Mathematics “F. Casorati”, University of Pavia, Via Ferrata 1, 27100 Pavia, Italy Accepted 6 August 2010 ABSTRACT In this paper we provide a mathematical reconstruction of what might have been Gauss’ own derivation of the linking number of 1833, providing also an alternative, explicit proof of its modern interpretation in terms of degree, signed crossings and inter- section number. The reconstruction presented here is entirely based on an accurate study of Gauss’ own work on terrestrial magnetism. A brief discussion of a possibly indepen- dent derivation made by Maxwell in 1867 completes this reconstruction. Since the linking number interpretations in terms of degree, signed crossings and intersection index play such an important role in modern mathematical physics, we offer a direct proof of their equivalence. Explicit examples of its interpretation in terms of oriented area are also provided. Keywords: Linking number; potential; degree; signed crossings; intersection number; oriented area. Mathematics Subject Classification 2010: 57M25, 57M27, 78A25 1. Introduction The concept of linking number was introduced by Gauss in a brief note on his diary in 1833 (see Sec. 2 below), but no proof was given, neither of its derivation, nor of its topological meaning. Its derivation remained indeed a mystery.
    [Show full text]
  • On the Covariant Representation of Integral Equations of the Electromagnetic Field
    On the covariant representation of integral equations of the electromagnetic field Sergey G. Fedosin PO box 614088, Sviazeva str. 22-79, Perm, Perm Krai, Russia E-mail: [email protected] Gauss integral theorems for electric and magnetic fields, Faraday’s law of electromagnetic induction, magnetic field circulation theorem, theorems on the flux and circulation of vector potential, which are valid in curved spacetime, are presented in a covariant form. Covariant formulas for magnetic and electric fluxes, for electromotive force and circulation of the vector potential are provided. In particular, the electromotive force is expressed by a line integral over a closed curve, while in the integral, in addition to the vortex electric field strength, a determinant of the metric tensor also appears. Similarly, the magnetic flux is expressed by a surface integral from the product of magnetic field induction by the determinant of the metric tensor. A new physical quantity is introduced – the integral scalar potential, the rate of change of which over time determines the flux of vector potential through a closed surface. It is shown that the commonly used four-dimensional Kelvin-Stokes theorem does not allow one to deduce fully the integral laws of the electromagnetic field and in the covariant notation requires the addition of determinant of the metric tensor, besides the validity of the Kelvin-Stokes theorem is limited to the cases when determinant of metric tensor and the contour area are independent from time. This disadvantage is not present in the approach that uses the divergence theorem and equation for the dual electromagnetic field tensor.
    [Show full text]
  • Electromagnetic Field Theory
    Lecture 4 Electromagnetic Field Theory “Our thoughts and feelings have Dr. G. V. Nagesh Kumar Professor and Head, Department of EEE, electromagnetic reality. JNTUA College of Engineering Pulivendula Manifest wisely.” Topics 1. Biot Savart’s Law 2. Ampere’s Law 3. Curl 2 Releation between Electric Field and Magnetic Field On 21 April 1820, Ørsted published his discovery that a compass needle was deflected from magnetic north by a nearby electric current, confirming a direct relationship between electricity and magnetism. 3 Magnetic Field 4 Magnetic Field 5 Direction of Magnetic Field 6 Direction of Magnetic Field 7 Properties of Magnetic Field 8 Magnetic Field Intensity • The quantitative measure of strongness or weakness of the magnetic field is given by magnetic field intensity or magnetic field strength. • It is denoted as H. It is a vector quantity • The magnetic field intensity at any point in the magnetic field is defined as the force experienced by a unit north pole of one Weber strength, when placed at that point. • The magnetic field intensity is measured in • Newtons/Weber (N/Wb) or • Amperes per metre (A/m) or • Ampere-turns / metre (AT/m). 9 Magnetic Field Density 10 Releation between B and H 11 Permeability 12 Biot Savart’s Law 13 Biot Savart’s Law 14 Biot Savart’s Law : Distributed Sources 15 Problem 16 Problem 17 H due to Infinitely Long Conductor 18 H due to Finite Long Conductor 19 H due to Finite Long Conductor 20 H at Centre of Circular Cylinder 21 H at Centre of Circular Cylinder 22 H on the axis of a Circular Loop
    [Show full text]
  • Units and Magnitudes (Lecture Notes)
    physics 8.701 topic 2 Frank Wilczek Units and Magnitudes (lecture notes) This lecture has two parts. The first part is mainly a practical guide to the measurement units that dominate the particle physics literature, and culture. The second part is a quasi-philosophical discussion of deep issues around unit systems, including a comparison of atomic, particle ("strong") and Planck units. For a more extended, profound treatment of the second part issues, see arxiv.org/pdf/0708.4361v1.pdf . Because special relativity and quantum mechanics permeate modern particle physics, it is useful to employ units so that c = ħ = 1. In other words, we report velocities as multiples the speed of light c, and actions (or equivalently angular momenta) as multiples of the rationalized Planck's constant ħ, which is the original Planck constant h divided by 2π. 27 August 2013 physics 8.701 topic 2 Frank Wilczek In classical physics one usually keeps separate units for mass, length and time. I invite you to think about why! (I'll give you my take on it later.) To bring out the "dimensional" features of particle physics units without excess baggage, it is helpful to keep track of powers of mass M, length L, and time T without regard to magnitudes, in the form When these are both set equal to 1, the M, L, T system collapses to just one independent dimension. So we can - and usually do - consider everything as having the units of some power of mass. Thus for energy we have while for momentum 27 August 2013 physics 8.701 topic 2 Frank Wilczek and for length so that energy and momentum have the units of mass, while length has the units of inverse mass.
    [Show full text]
  • Electro Magnetic Fields Lecture Notes B.Tech
    ELECTRO MAGNETIC FIELDS LECTURE NOTES B.TECH (II YEAR – I SEM) (2019-20) Prepared by: M.KUMARA SWAMY., Asst.Prof Department of Electrical & Electronics Engineering MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY (Autonomous Institution – UGC, Govt. of India) Recognized under 2(f) and 12 (B) of UGC ACT 1956 (Affiliated to JNTUH, Hyderabad, Approved by AICTE - Accredited by NBA & NAAC – ‘A’ Grade - ISO 9001:2015 Certified) Maisammaguda, Dhulapally (Post Via. Kompally), Secunderabad – 500100, Telangana State, India ELECTRO MAGNETIC FIELDS Objectives: • To introduce the concepts of electric field, magnetic field. • Applications of electric and magnetic fields in the development of the theory for power transmission lines and electrical machines. UNIT – I Electrostatics: Electrostatic Fields – Coulomb’s Law – Electric Field Intensity (EFI) – EFI due to a line and a surface charge – Work done in moving a point charge in an electrostatic field – Electric Potential – Properties of potential function – Potential gradient – Gauss’s law – Application of Gauss’s Law – Maxwell’s first law, div ( D )=ρv – Laplace’s and Poison’s equations . Electric dipole – Dipole moment – potential and EFI due to an electric dipole. UNIT – II Dielectrics & Capacitance: Behavior of conductors in an electric field – Conductors and Insulators – Electric field inside a dielectric material – polarization – Dielectric – Conductor and Dielectric – Dielectric boundary conditions – Capacitance – Capacitance of parallel plates – spherical co‐axial capacitors. Current density – conduction and Convection current densities – Ohm’s law in point form – Equation of continuity UNIT – III Magneto Statics: Static magnetic fields – Biot‐Savart’s law – Magnetic field intensity (MFI) – MFI due to a straight current carrying filament – MFI due to circular, square and solenoid current Carrying wire – Relation between magnetic flux and magnetic flux density – Maxwell’s second Equation, div(B)=0, Ampere’s Law & Applications: Ampere’s circuital law and its applications viz.
    [Show full text]
  • 6.007 Lecture 5: Electrostatics (Gauss's Law and Boundary
    Electrostatics (Free Space With Charges & Conductors) Reading - Shen and Kong – Ch. 9 Outline Maxwell’s Equations (In Free Space) Gauss’ Law & Faraday’s Law Applications of Gauss’ Law Electrostatic Boundary Conditions Electrostatic Energy Storage 1 Maxwell’s Equations (in Free Space with Electric Charges present) DIFFERENTIAL FORM INTEGRAL FORM E-Gauss: Faraday: H-Gauss: Ampere: Static arise when , and Maxwell’s Equations split into decoupled electrostatic and magnetostatic eqns. Electro-quasistatic and magneto-quasitatic systems arise when one (but not both) time derivative becomes important. Note that the Differential and Integral forms of Maxwell’s Equations are related through ’ ’ Stoke s Theorem and2 Gauss Theorem Charges and Currents Charge conservation and KCL for ideal nodes There can be a nonzero charge density in the absence of a current density . There can be a nonzero current density in the absence of a charge density . 3 Gauss’ Law Flux of through closed surface S = net charge inside V 4 Point Charge Example Apply Gauss’ Law in integral form making use of symmetry to find • Assume that the image charge is uniformly distributed at . Why is this important ? • Symmetry 5 Gauss’ Law Tells Us … … the electric charge can reside only on the surface of the conductor. [If charge was present inside a conductor, we can draw a Gaussian surface around that charge and the electric field in vicinity of that charge would be non-zero ! A non-zero field implies current flow through the conductor, which will transport the charge to the surface.] … there is no charge at all on the inner surface of a hollow conductor.
    [Show full text]