DOCSLIB.ORG

Modeling and Control of Physical Systems: an Approach Based on Energy and Interconnection∗

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling and Control of Physical Systems: an Approach Based on Energy and Interconnection∗ Modeling and control of physical systems: an approach based on energy and interconnection∗ Bernhard Maschke.1/, Romeo Ortega.2/, Arjan van der Schaft.3/ .1/Laboratoire d’Automatisme Industriel, CNAM, 21 rue Pinel, 75013 Paris, France .2/Lab. des Signaux et Syst`emes, Sup´elec, Plateau de Moulon, 91192 Gif sur Yvette, France .3/Fac. of Mathematical Sciences, University of Twente, P.O. Box 217, 7500AE Enschede, The Netherlands [email protected],[email protected] [email protected] Abstract implications for regulation and tracking, has undergone a re- markable revival. This last development was also spurred by It is discussed how network modeling of lumped-parameter work in robotics on the possibilities of shaping by feedback physical systems naturally leads to a geometrically defined the physical energy in such a way that it can be used as a suit- class of systems, called port-controlled Hamiltonian systems able Lyapunov function for the control purpose at hand, see with dissipation. The structural properties of these systems e.g. the influential paper [38]. This has led to what is some- are investigated, in particular the existence of Casimir func- times called passivity-based control, see e.g. [23, 29, 10]. tions and their implications for stability. It is shown how a Many other important developments have taken place, and power-conserving interconnection of port-controlled Hamil- much attention has been paid to special subclasses of systems tonian systems defines another port-controlled Hamiltonian like mechanical systems with nonholonomic constraints. All system, and how this may be used for design and for control this has resulted in a very lively research in nonlinear control, by shaping the internal energy. Extensions to implicit system with many actual and potential applications. descriptions (constraints, no a priori input-output structure) In this mini-course we want to stress the importance of and distributed parameter systems are indicated. modeling for nonlinear control. Of course, this is com- keywords: nonlinear control, modeling, passivity, Hamil- mon practice for working engineers, but a general theoreti- tonian systems, interconnection cal framework for modeling is also of utmost importance for the development of nonlinear control theory. We limit our- 1 Introduction selves to lumped-parameter physical systems, such as me- chanical and electrical systems as well as electro-mechanical Nonlinear systems and control theory has witnessed tremen- systems, although in principle the framework can be ex- dous developments over the last three decades, see for ex- tended to distributed-parameter systems, see [14]. We dis- ample the textbooks [9, 22]. Especially the introduction of cuss how network modeling of such systems naturally leads geometric tools like Lie brackets of vector fields on mani- to a geometrically defined class of systems called port- folds has greatly advanced the theory, and has enabled the controlled Hamiltonian systems with dissipation (PCHD sys- proper generalization of many fundamental concepts known tems). These systems are determined by an internal intercon- for linear control systems to the nonlinear world. While the nection structure, a Hamiltonian defined as the total stored emphasis in the eighties has been primarily on the structural energy, and a resistive structure. Historically, the Hamilto- analysis of smooth nonlinear dynamical control systems, in nian approach has its roots in analytical mechanics and starts the nineties this has been combined with analytic techniques from the principle of least action, via the Euler-Lagrange for stability, stabilization and robust control, leading e.g. to equations and the Legendre transform, towards the Hamil- backstepping techniques and nonlinear H∞- control. More- tonian equations of motion. On the other hand, the network over, in the last decade the theory of passive systems, and its approach stems from electrical engineering, and constitutes a cornerstone of systems theory. While most of the analysis of ∗ This paper is an adapted and expanded version of the paper “Port- physical systems has been performed within the Lagrangian controlled Hamiltonian systems: towards a theory for control and design and Hamiltonian framework, the network modelling point of of nonlinear physical systems”, by A.J. van der Schaft, which is going to appear in the Journal of the Society of Instrument and Control Engineers view is prevailing in modelling and simulation of (complex) (SICE) of Japan. Part of this material can be also found in [29]. physical systems. The framework of PCHD systems com- bines both points of view, by associating with the intercon- equations nection structure of the network models a geometric struc- q˙ = @H .q; p/.=M−1.q/p/ ture given by a Poisson structure, or more generally a Dirac @p (4) structure. Dirac structures encompass Poisson structures, but p˙=−@H.q;p/+− they allow a considerable generalization since they also de- @q scribe systems with constraints as arising from the intercon- where nection of sub-systems. Furthermore, Dirac structures allow H.q; p/ = 1 pT M−1.q/ p + P.q/ to extend the Hamiltonian description of distributed param- 2 (5) . = 1 ˙T . / ˙ + . // eter systems by including boundary conditions, leading to a 2 q M q q P q non-zero energy balance at the boundary of the spatial do- is the total energy of the system. The equations (4) are called main, see [14]. the Hamiltonian equations of motion, and H is called the In the present paper we will restrict ourselves for simplicity Hamiltonian. The following energy balance immediately to PCHD systems that are defined with respect to a Poisson follows from (4): structure. The structural properties of these PCHD systems d @T H @T H H = @ .q; p/q˙+ @ .q; p/p˙ are investigated through geometric tools stemming from the dt q p (6) = @T H . ; /− =˙T−; theory of Hamiltonian systems. It is indicated how the inter- @p q p q connection of PCHD systems leads to another PCHD system, expressing that the increase in energy of the system is equal and how this may be exploited for control and design. In par- to the supplied work (conservation of energy). ticular, we investigate the existence of Casimir functions for If the potential energy is bounded from below,thatis∃C> the feedback interconnection of a plant PCHD system and a −∞ such that P.q/ ≥ C, then it follows that (4) with in- controller PCHD system, leading to a reduced PCHD system puts u = − and outputs y =˙qis a passive (in fact, lossless) on invariant manifolds with shaped energy. We thus provide state space system with storage function H.q; p/ − C ≥ 0 an interpretation of passivity-based control from an intercon- (see e.g. [39, 8, 29] for the general theory of passive and dis- nection point of view. sipative systems). Since the energy is only defined up to a constant, we may as well take as potential energy the func- 2 Port-controlled Hamiltonian systems tion P.q/ − C ≥ 0, in which case the total energy H.q; p/ becomes nonnegative and thus itself is the storage function. 2.1 From the Euler-Lagrange and Hamiltonian equa- System (4) is an example of a Hamiltonian system with col- tions to port-controlled Hamiltonian systems located inputs and outputs, which more generally is given in the following form Let us briefly recall the standard Euler-Lagrange and Hamil- @ tonian equations of motion. The standard Euler-Lagrange ˙ = H . ; /; . ; / = . ;:::; ; ;:::; / q @ q p q p q1 qk p1 pk equations are given as p @ H.;/+./; ∈ m; ˙ =− R d @L @L p @ qp Bqu u (7) .q;q˙/ − .q;q˙/ = −; (1) q dt @q˙ @q @ T H . ; /.=T m; y = B .q/ q p B.q/q˙/; y ∈ R T @p where q = .q1;:::;qk/ are generalized configuration co- ordinates for the system with k degrees of freedom, the La- Here B.q/ is the input force matrix, with B.q/u denoting the ∈ m grangian L equals the difference K − P between kinetic en- generalized forces resulting from the control inputs u R . T . ; / ergy K and potential energy P,and−=.−1;:::;−k/ is the The state space of (7) with local coordinates q p is usually vector of generalized forces acting on the system. Further- called the phase space. Normally m < k, in which case we @L speak of an underactuated system. more, @q˙ denotes the column-vector of partial derivatives of = T . / ˙ L.q; q˙/ with respect to the generalized velocities q˙1;:::;q˙k, Because of the form of the output equations y B q q we @L again obtain the energy balance and similarly for @q . In standard mechanical systems the ki- netic energy K is of the form dH .q.t/; p.t// = uT .t/y.t/ (8) 1 dt K.q; q˙/ = q˙T M.q/q˙ (2) 2 and if H is bounded from below, any Hamiltonian system (7) is a lossless state space system. For a system-theoretic × . / where the k k inertia (generalized mass) matrix M q is treatment of Hamiltonian systems (7), we refer to e.g. [3, 26, symmetric and positive definite for all q. In this case the 27,4,22]. = . ;:::; /T vector of generalized momenta p p1 pk , defined A major generalization of the class of Hamiltonian systems = @L for any Lagrangian L as p @q˙ , is simply given by (7) is to consider systems which are described in local coor- dinates as p = M.q/q˙; (3) @H m ˙ = . / . / + . / ; ∈ ; ∈ R x J x @x x g x u x X u T and by defining the state vector .q1;:::;qk;p1;:::;pk/ (9) T @H m the k second-order equations (1) transform into 2k first-order = . / . /; ∈ R y g x @x x y Here J.x/ is an n × n matrix with entries depending with H.Q;'1;'2/ := H1.'1/ + H2.'2/ + H3.Q/ the total smoothly on x, which is assumed to be skew-symmetric energy.
Load more

Recommended publications
  • Fourth International Conference on Porous Media and Its Applications in Science, Engineering and Industry
    Program Fourth International Conference on Porous Media and its Applications in Science, Engineering and Industry June 17-22, 2012 Potsdam, Germany Chair Kambiz Vafai University of California, Riverside, USA Co-Chairs Adrian Bejan Duke University, USA Akira Nakayama Shizuoka University, Japan Engineering Conferences International 32 Broadway, Suite 314 New York, NY 10004, USA Phone: 1 - 212 - 514 - 6760, Fax: 1 - 212 - 514 - 6030 www.engconfintl.org – [email protected] Seminaris Seehotel Potsdam An der Pirschneide 40 D-14471 Potsdam Germany Tel: +49 (0) 331 9090-0 Fax: +49 (0) 331 9090-900 Engineering Conferences International (ECI) is a not-for-profit global engineering conferences program, originally established in 1962, that provides opportunities for the exploration of problems and issues of concern to engineers and scientists from many disciplines. ECI BOARD MEMBERS Barry C. Buckland, President Peter Gray Michael King Raymond McCabe David Robinson William Sachs Eugene Schaefer P. Somasundaran Deborah Wiley Chair of ECI Conferences Committee: William Sachs ECI Technical Liaison for this conference: Frank Schmidt ECI Director: Barbara K. Hickernell ECI Associate Director: Kevin M. Korpics ©Engineering Conferences International International Organizing Committee Prof. Antonio Barletta (Università di Bologna, Italy), Prof. Jacob Bear (Technion, Israel), Prof. Adrian Bejan (Duke University, USA), Prof. Faruk Civan (University of Oklahoma, USA), Dr. Fabien Frizon (CEA Marcoule, France), Dr. Robin Gerlach (Montana State University, USA), Prof. S. Majid Hassanizadeh (Utrecht University, Netherlands), Prof. Reiner Helmig (Universitaet Stuttgart, Germany), Prof. Rudolf Hilfer (Universität Stuttgart, Germany), Prof. Massoud Kaviany (University of Michigan, USA), Prof. Arzhang Khalili (Max Planck Institute for Marine Microbiology, Germany), Prof. Andrey Kuznetsov (North Carolina State University, USA), Louis-Philippe Lefebvre (National Research Council, Canada), Dr.
    [Show full text]
  • Apply for a Research Assignment in the Faculty of Engineering Technology, University of Twente
    How to … apply for a research assignment in the Faculty of Engineering Technology, University of Twente Target group of this document: students, - who are currently studying full time at a university outside the Netherlands, - who are interested in doing a research assignment within the Faculty of Engineering Technology, - and have found a potential supervisor within one of the research departments of the Faculty of Engineering Technology (www.utwente.nl/en/et/research/) 1. Introduction 1 1.1. Terminology 1 1.2. Important remarks befóre you start with the application 2 2. Application procedure 2 2.1. Nomination vs. application 2 2.2. Continuing with the application form 4 2.3. Continuing the application process 5 1. Introduction 1.1. Terminology When you receive/read this document, you have shown an interest in joining the Faculty of Engineering Technology for a certain period of time, to conduct a research assignment under the supervision of a member of staff of this Faculty. For you, this research assignment might serve as your master assignment, bachelor assignment, thesis work, graduation work, internship, placement, external training, etc. For us, this research assignment is always considered as a ‘placement’, and will be booked either as a so-called “Capita selecta” course (MSc students; different course codes) or as “Research assignment for exchange students of the Faculty of Engineering Technology” (BSc level; course code: 201800519). In your communication with a member of staff make it clear that you are not asking to be accepted for a ‘graduation assignment’, but for a ‘research assignment which you will use at home for your graduation’.
    [Show full text]
  • Scope Topics Multibody System Dynamics Colloquia Supporting
    Call for Papers Scope Topics The language of the Colloquium is English. Authors The colloquium addresses the method of multibody • Numerically efficient multibody system dynamics wishing to contribute to the Colloquium are invited to system dynamics for advanced technologies and techniques; submit a two page abstract to the chairmen by e-mail engineering design for which a numerical efficient • Design principles for exact constraint; before October 12, 2011. The abstract shall follow the approach is crucial. In particular a designer can take • Underconstraint and overconstraint mechanical format of the Colloquium abstract template (see the significant advantage of model based dynamical systems; web site). Authors will receive notification of analysis. The numerical methods applied for multibody • Underactuated and overactuated compliant acceptance of their proposed contribution by systems dynamics have proved to offer solutions for mechanisms; November 16, 2011. An abstracts booklet containing the analysis of systems with interconnected rigid and • Flexible multibody dynamics and reduced order all the contributions will be given to the delegates at flexible bodies subject to various loads and undergoing modelling; the Colloquium. The number of participants will be complex motion. While high accuracy can be obtained • Mechatronic design and control systems; limited and preference will be given to active with extended models including a large number of • Parameter optimisation and manufacturing researchers in the field. Confirmation of participation degrees of freedom, there is a clear need for tolerances; in the Colloquium by the authors will be required numerically efficient techniques that still offer an • Simulation for engineering design; when papers are accepted. Only confirmed adequate level of accuracy.
    [Show full text]
  • Innovative Teaching and Learning Methods
    The Future of Engineering Education Parallel Sessions I Innovative Teaching and Learning Methods Time: 2 April 2020, 2pm – 4pm Venue: Congress Centre Darmstadtium Abstract The session will start with presentations of a wide variety of innovative teaching and learning tech- nologies and methodologies. The talks deal with virtual reality (VR) and open source technology, vir- tual exchange programs between partner universities, students solving tasks in interdisciplinary teams, and train the teacher in a way that they can awaken enthusiasm among students for technical issues. After the presentations, all participants will actively be involved to discuss the influence these new methodologies and technologies have on the organization as a whole and the student and teacher specifically. Among other questions: Does the use of new technologies influence the skills teachers need to adapt to these new technologies? Which social skills are necessary to train the stu- dent to face the societal challenges of the future? Keywords and concepts Virtual reality, New Technologies in Teaching, Motivational Methods Contributors Professor Albert Albers (Karlsruhe Institute of Technology, KIT) Professor Albert Albers has been head of the IPEK – Institute of Product Engineering since 1996. After his studies of mechanical engineering at the University of Hannover from 1978 to 1983, Albers had an assistantship at the Institute of Machine Elements and Engineering Design and obtained his doctorate in 1987. From 1986 to 1988 Albers had a position as a senior engineer at the Institute of Machine Elements and Engineering Design at the University of Hannover until he started his career in industry at LuK, a company of the Schaef-er-Group with focus on clutch- and gear-systems.
    [Show full text]
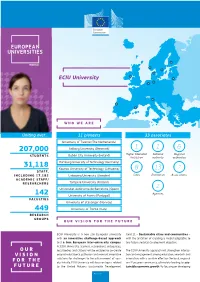
  • ECIU University
    ECIU University WHO WE ARE Uniting over… 11 pioneers 33 associates University of Twente (The Netherlands) 1 1 6 207,000 Aalborg University (Denmark) Dublin City University (Ireland) Higher Education National Regional STUDENTS Institution authority authorities Hamburg University of Technology (Germany) 31,118 Kaunas University of Technology (Lithuania) 8 13 2 STAFF, INCLUDING 17,182 Linköping University (Sweden) Cities Enterprises Associations ACADEMIC STAFF/ Tampere University (Finland) RESEARCHERS 2 Universitat Autònoma de Barcelona (Spain) Agencies 142 University of Aveiro (Portugal) FACULTIES University of Stavanger (Norway) 449 University of Trento (Italy) RESEARCH GROUPS OUR VISION FOR THE FUTURE ECIU University is a new pan-European university Goal 11 – Sustainable cities and communities – with an innovative challenge-based approach with the ambition of creating a model adaptable to and a true European inter-university campus. any future societal development objective. At ECIU University, learners, researchers, enterprises, OUR local bodies and citizens will be enabled to co-create The ECIU University approach will strengthen interac- VISION original educational pathways and relevant innovative tion and engagement among education, research and solutions for challenges to the advancement of soci- innovation, with a positive effect on the local, regional FOR THE ety. Initially, ECIU University will focus on topics related and European community, ultimately leading to sus- FUTURE to the United Nations Sustainable Development tainable
    [Show full text]
  • M06-Attendies
    Graduate School on Control 2011 M6 - Cooperative Navigation and Control of Multiple Robotic Vehicles from 21/02/2011 to 25/02/2011 Family Name First Name Company Service City Country Email Akbati Onur Yildiz Technical University Control & Automation Dept.Istanbul Turkey [email protected] Attia Rachid Université de Haute-Alsace, MIPS Mulhouse Cedex France [email protected] Chaos García Dictino UNED Assistant Professor madrid Spain [email protected] Colombo Alessio DISI - University of Trento PhD student Povo (TN) Italy [email protected] Colombo Leonardo Institito de Cienias Matematicas-ConsejoPh. Superior D student e InvestigacionesMadrid Científicas (ICMAT-CSIC) Spain [email protected]; [email protected] Dorogush Elena Moscow State University postgraduate student Moscow Russia [email protected] Esqueda Donovan Supelec Automatique Gif sur Yvette France [email protected] Fabregas Acosta Ernesto National University for Distance Education of Spain (UNED) Madrid Spain [email protected] Feng Xinkui LSS Supelec Orsay France [email protected] Fioravanti Andre Supelec l2s Gif-sur-Yvette France [email protected] Geamanu Marcel Stefan L2S Gif-sur-Yvette France [email protected] Jafarian Matin University of Twente; Faculty of Engineering Technology (CTW) Enschede The [email protected] Jiménez Fernando ICMAT-CSIC Researcher-Grad. StudentMadrid Spain [email protected] Makarem Laleh EPFL Lausanne Switzerland [email protected] Mansal Fulgence UCAD Departement
    [Show full text]
  • University of Twente: the Entrepreneurial University of the Netherlands Through Hi-Tech and Human Touch
    University of Twente: The entrepreneurial university of the Netherlands through hi-tech and human touch Enschede, Netherlands 1 General Information Title University of Twente Pitch The entrepreneurial university of the Netherlands through hi-tech and hu- man touch Organisations University of Twente and Kennispark Twente Country The Netherlands Authors Arno Meerman (University Industry Innovation Network) Nature of Collaboration in R&D Lifelong learning Commercialisation of R&D Joint curriculum design and interaction results delivery Mobility of staff Mobility of students Academic entrepreneurship Student entrepreneurship Governance Shared resources Supporting Strategic Structural mechanism Operational Policy Summary The University of Twente (UT) together with the Kennispark Twente, are key drivers behind regional innovation and growth and the renaissance of the Twente region. From its foundation in 1961 during difficult local economic conditions, UT has grown into a world-class entrepreneurial university through its top-to-bottom innovative and entrepreneurial institutional cul- ture, its human resource strategy (i.e. hiring entrepreneurial and innovative staff members) and its strong regional network. Their activities have led to over 100 new start-ups per year on average, over 1,000 spin-offs still opera- tional to date, and in excess of 20,000 jobs created. The UT spin-offs also ac- count for 10% of the fastest growing high-tech companies in the Benelux countries. All of these factors, together with the number one Valorisation University Award in the Netherlands in 2015, highlight why UT has a world- wide reputation for entrepreneurship. 2 Introduction & Overview 1. BACKGROUND The University of Twente (UT) is a public higher education institution located in Enschede (The Neth- erlands) with approximately 3,000 staff members, 9,700 students, and degree programmes offered in engineering, social and behavioural sciences.
    [Show full text]
  • Télécom Paristech / LTCI
    Research Report 2009-2011 ~ Télécom ParisTech / LTCI février 2012 Laboratoire Traitement et Communication de l’Information - UMR 5141 Télécom ParisTech - CNRS Research Report 2009–2011 Laboratoire Traitement et Communication de l’Information Institut Tel´ ecom´ - Tel´ ecom´ ParisTech & CNRS February 2012 2 Contents 1 General Survey 9 1.1 Organization . .9 1.1.1 Tel´ ecom´ ParisTech and Institut Tel´ ecom´ . .9 1.1.2 Tel´ ecom´ ParisTech and LTCI (Laboratory for Communication and Process- ing of Information) . 10 1.1.3 Tel´ ecom´ ParisTech and ParisTech . 10 1.1.4 Organization at LTCI . 11 1.1.5 Personnel in the Service of Research . 11 1.2 Research at a glance . 12 1.2.1 Positioning of Telecom ParisTech research . 12 1.2.2 Major orientations in the period . 13 1.2.3 Highlights of research at Telecom ParisTech over the period . 14 1.2.4 International Research program . 16 1.2.5 Scientific production . 16 1.2.6 Participation to Investissements d’Avenir .................... 17 I Communications and Electronics 21 2 Digital Communications 25 2.1 Objectives . 26 2.2 Main Results . 27 2.2.1 Wireless Network Optimization . 27 2.2.2 Coding for single-user communication . 28 2.2.3 Optical communications . 30 2.2.4 Security issues . 30 2.2.5 Tools for Information Theory and Statistics . 31 2.3 References . 32 2.3.1 ACL: Articles in ISI-Indexed Journals . 32 2.3.2 ACTI: Articles in Proceedings of International Conferences . 33 2.3.3 OS: Books and Book Chapters . 36 2.3.4 AP: Other productions .
    [Show full text]
  • Annual Report 2019
    Department of Ghent University Materials, Textiles and Department of Materials, Textiles and Chemical Engineering (MaTCh) Chemical Engineering Centre for Textile Science and Engineering (MaTCh) ANNUAL REPORT Technologiepark 70A Tech Lane Ghent Science Park – Campus A (A5b and A5c) 9052 Ghent (Zwijnaarde) BELGIUM Tel: +32 9 264 57 35 Fax: +32 9 264 58 46 2019 http://textiles.UGent.be @UGentTextiles UGent Centre for Textile Science and Engineering Centre for Textile Science and Engineering The one and only objective and comprehensive textile group in the Benelux ISO/IEC17025 055-test Cover: Nanofibre filters for environmental challenges (Visual by Timo Meireman). 90 Years of Excellence through Passion & Commitment ‘Centre of Excellence’ for Textile Science and Engineering 7 CONTENTS VOORWOORD 9 FOREWORD 11 GENERAL 13 EDUCATION 18 INTERNATIONAL RELATIONS 28 RESEARCH AND INNOVATION 37 SERVICES TO INDUSTRY 70 PUBLICATIONS 75 9 VOORWOORD Het jaar 2019 was een bijzonder en buitengewoon gunstig jaar voor de textielafdeling van de Universiteit Gent. Het onderwijs kende een nieuw hoogtepunt met ruime interesse. Het onderzoek floreerde als nooit tevoren met tal van innovatieve en toekomstgerichte activiteiten. Wat betreft de wetenschappelijke dienstverlening werden alle records gebroken : nooit eerder was er zo een grote interactie met de (Europese) industrie en nooit eerder was de impact naar die industrie zo uitgesproken. De internationale uitstraling van de textielactiviteiten van het textielcentrum was nooit zo groot. Dit werd bevestigd door de deelname aan het congres AUTEX 2019 in Gent onder de titel Textiles at the Crossroads www.autex2019.org Meer dan 300 deelnemers uit nagenoeg 50 landen gaven het beste van zichzelf en bewezen dat textiel­ onderzoek een multidisciplinaire activiteit is, gedragen door een grote mondiale familie met zin voor innovatie en aandacht voor duurzaamheid op het hoogste wetenschappelijke en technologische vlak.
    [Show full text]
  • European Partner Universities to University of Southern Denmark
    European partner universities to University of Southern Denmark Austria FH Joanneum FHS Kufstein Tirol University of Applied Sciences Graz University of Technology Management Center Innsbruck MODUL University Vienna Salzburg University of Applied Sciences University of Applied Sciences Technikum Wien University of Applied Sciences Upper Austria University of Applied Sciences Wiener Neustadt University of Graz University of Vienna Belgium Ghent University Hasselt University ICHEC Brussels Management School KU Leuven Université Catholique de Louvain University College Gent Bulgaria Sofia University 'Saint Kliment Ohridski' Technical University of Sofia Croatia University of Zadar Cypern University of Cyprus Czech Republic Brno University of Technology Charles University in Prague Czech Technical University in Prague Czech University of Life Sciences Prague Masaryk University Metropolitan University Prague University of Economics, Prague University of Palacky University of Pardubice University of West Bohemia VSB - Technical University of Ostrava Denmark University of Greenland University of the Faroe Islands Estonia Tallinn University of Applied Sciences (TTK) Tallinn University of Technology University of Tartu Finland Hanken School of Economics Lappeenranta University of Technology Oulu University of Applied Sciences South-Eastern Finland University of Applied Sciences Tampere University of Applied Sciences (TAMK) Tampere University of Technology University of Eastern Finland University of Helsinki University of Jyväskylä University of
    [Show full text]
  • 2019 USF Nexus Initiative (UNI) Awards Request for Proposals
    1 2019 USF Nexus Initiative (UNI) Awards Request for Proposals Program Goals and Description The University of South Florida Nexus Initiative (UNI), administered through the Office of the Provost at USF, offers tenured/tenure-track and full-time research faculty members the opportunity to collaborate with global and national partners in research, scholarly, and innovative efforts with the potential to significantly advance current human understanding and address pressing societal needs. UNI has the following goals: (1) to enhance the research and scholarly activity of faculty members at USF by enabling a variety of partnerships that provide both intellectual and infrastructure stimulus to catalyze and extend ongoing work at USF; (2) to provide avenues for the exploration of joint research and scholarship with external partners and initiate activities currently not possible at USF; (3) to enable opportunities for developing sustained research and scholarship programs with high-impact researchers at other institutions through the submission and funding of joint grant proposals; and (4) to create opportunities for our best graduate students to expand the breadth of their research and scholarly experience through participation in multi-investigator (potentially interdisciplinary) inquiry. Proposals are requested for two avenues offering awards responsive to the broad goals of UNI: The USF Faculty Global Collaboration Initiative offers tenured/tenure-track and full-time research faculty members UNI Awards of up to $15,000 in annual support for travel and expense funds to collaborate with a colleague at an institution of higher education outside the U.S. to engage in research and scholarly activities. The USF Faculty National Collaboration Initiative offers tenured/tenure-track and full-time research faculty members UNI Awards of up to $10,000 in annual support for travel and expense funds to collaborate with a colleague at an institution of higher education within the U.S.
    [Show full text]
  • Viewed and Recommendations Were Given, These Conclusions Are Written Down in Chapter 7
    University of Twente EEMCS / Electrical Engineering Robotics and Mechatronics Image-Guided Control of a Continuum Robot S.L. (Sander) Janssen MSc Report Committee: Prof.dr.ir. S. Stramigioli Dr. S. Misra J. Jahya, MSc R.J. Roesthuis, MSc Ir. E.E.G. Hekman November 2012 Report nr. 030RAM2012 Robotics and Mechatronics EE-Math-CS University of Twente P.O. Box 217 7500 AE Enschede The Netherlands ! Abstract This study presents the development of a continuum robot which could serve as part of a surgical robot. Continuum robots, because of their dexterous nature and continuous shape are suited for minimally invasive surgery. Their inherent flexibility also reduces the risk of damage. Continuum robots have these properties due to the absence of discrete joints. Previous research in the domain of continuum robots has focused on developing kinematic and dynamic models. These models attempt to take in account as much of the inherent imperfections such as friction and fabrication errors as possible. This study instead focussed on showing that a simple kinematic model based on the ideal behaviour of the robot is sufficient when combined with a closed-loop controller with 3D position feedback. A continuum robot and its actuator have been developed. The continuum robot was tendon actuated. It consisted of a flexible nitinol backbone with four disc shaped tendon guides fixed equidistantly to each other to it. Two designs of robot were created: A 160 mm length robot with 5 mm radius tendon guides and a 160 mm one with 10 mm radius tendon guides. The actuator was fitted with four motors to pull the tendons and had a translation stage for an insertion movement.
    [Show full text]