DOCSLIB.ORG

Landmarks of Science in Early and Classical India

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Landmarks of Science in Early and Classical India Landmarks of Science in Early and Classical India Michel Danino Email: [email protected] Based on lectures given at Amrita Vishwa Vidyapeetham, Coimbatore, January 2010, and IIT-Kanpur, February 2010 For pritivateciltiirculation only. Note When we study the history of science in India, we come across a variety of perspectives. At one end of the spectrum, some scholars find no science in ancient India. To them, her contributions are limited, at best, to the decimal place-value system of numeral notation; otherwise, what passes off as Indian science was actually bdborrowed from the BblBabylon ians, the GkGreeks, the Chinese and the AbArabs. At the other end, overenthusiastic exponents have tried to portray early Indian scientists as creators of virtually all science, including gravitation, the theory of RltiitRelativityor quantum phihysics, and itinventors of wondrous machines such as vimânas or nuclear weapons. Both stands are untenable. There are many high achievements in the history of science in IdiIndia, btbut the iir dldevelopment was, as elhlsewhere, a gradldual process, rich in brilliant insights but also, at times, in errors or approximations. This presentation offers a overview of the evolution of science in early and clillassical IdiIndia; it titries tostiktrikeamiddlepath and to present highli g htsas objectively as possible. Targeting students, it avoids technical developments and claims no completeness. CtCommentsarewelcome. I. Pre-Siddhantic* DlDevelopmen ts * Siddhânta = “principle”, “conclusion”, but in the context of scientific literature, a treatise. This era is inaugurated by Aryabhâta at the end of the 5th century CE. 1. Neolithic & megalithic antecedents Burzahom, Kashmir (Neolithic , 3000–1500 BCE). Perhaps a supernova 7, 000 years ago. (H. Joglekar, Mayank Vahia & others) Bomai, Kashmir. The concentric circles may indicate a comet impact. (Mayank Vahia & others) Calendrical sticks noting the phases of the moon (Andamans, c.10000 BCE) In every ancient culture, early man regarded the universe as something vast, mysterious and sacred, and tried to relate to it in every possible way: through religion, through customs, and later through science. In megalithic monuments, for instance ((,above, stone circles at Brahmagiri near Myy,sore, studied by N.K. Rao), we find alignments with the sunrise at the solar solstice. Such studies of early monuments have long been conducted in the West but are only beginning in India. 2. Indus-Sarasvati Civilization First steps of technology and science in the protohistoric era* The east-west alignment of the main streets of Mohenjo-daro’s “citadel” (or acropolis, left) was based on the Pleiades star cluster (Krittika), which rose due east at the time; it no longer does because of the precession of the equinoxes. (German archaeologist Holger Wanzke, “Axis systems and orientation at Mohenjo-daro”, 1987) The mystery of Mohenjo-daro’s “ring stones” (above right):the small drilled holes (see red arrows), showed the stones were used to track the path of the sun through the year, as seen from Mohenjo-daro. Such evidences demonstrate the first steps in observational astronomy. There are other hints, such as possible * For technology, p lease see separate pdf file on astronomical symbolism on a few seals. (Finnish scholar Erkka this civilization. Maulan, “The Calendar Stones from Mohenjo-daro”, 1984) A rudimentary decimal system The standardized Harappan system of weights followed a dual binary- decimal progression: • 1 (= 0.86 g), 2, 4, 8, 16, 32, 64; • then, instead of continuing with the geometric progression: • 160, 200, 320, 640, 1,600, 3,200, 6,400, 8,000, 12,800; • therefore tens, hundreds and thousands of previous units. Note: This does not mean that the Harappans noted their numbers in a decimal manner (that is virtually impossible, as this development comes much later). Several other ancient civilizations also used multiples of 10 withou t a deci mal syst em of numeral not ati ons. Linear units related to those of historical times • Lothal’s measuring scale (bottom left, 27 graduations spanning 46 mm): 1 unit = 1.77 mm. • V. Mainkar in 1984: 10 Lothal units come close to the Arthashâstra’s angula or digit (1.778 cm in his estimate). • Kalibangan’s terracotta scale: a unit of 1.75 cm (analyzed by Prof. R. Balasubramaniam, IIT-Kanpur). • ItIn contemporary EtdMti(ltiChiGJEgypt and Mesopotamia (later in China, Greece, Japan, or the Roman Empire), the traditional digit fluctuated between 1.6 and 1.9 cm . • Dholavira’s successive enclosures follow strict ratios (()left), evidence of specific concepts of auspiciousness, sacred proportions, etc. • It is possible to calculate the unit of length used in planning Dholavira: 1.9 m (108 times 1.76 cm, the Harappan angula). (Research by Michel Danino.) 3. Historical Era: pre-Siddhantic* mathematics * Siddhânta = principle, conclusion, but in the context of scientific literature, a treatise. This era is inaugurated by Aryabhâta at the end of the 5th century CE. • Geometry of the Shulbasûtras (8th to 6th century BCE: shulba = rope): these four ancient texts deal with fire altars of various shapes. The altar, with 5 layers of 200 bricks each, symbolizes the universe, from the earth to the highest world. • The altars were constructed with bricks of specific shapes and area: the total area of the altar must always be carefully respected. It was generally 7½ square purushas, the pususha being, in the Shulbasûtras , the height of a man with his arm raised above his head. • This leads to precise but purely geometrical calculations (algebra did not exist yet). • The Shulbasûtras give a precise geometric expression of the so- called “Pythagorean theorem.” • Right angles were made by ropes marked to give the triads 3, 4, 5 and 5, 12, 13 (32 + 42 = 52, 52 + 122 = 132). • We should rename this theorem the “Shulba theorem”! Examples of other geometric operations in the Shulbasûtras: • “Squaring the circle” (and vice-versa): geometrically constructing a square having the same area as a given area. • Adding or subtracting the areas of two squares (to produce a single square). • Doubling the area of a square. • In the last construction, √2 works out to 577/408 or 1.414215, correct to the 5th decimal. (Same precision with √3.) • Pingala’s treatise Chhandashâstra or the science of verse meters (a few centuries BCE, Pingala being perhaps the brother of the famous grammarian Panini). • Notation of verse meters for verses with various numbers of syllables (6 in this case). • SllblSyllables are li liht(ght (lhlaghu)h) or heavy (guru)Th). The system of notation, spelling out every possible combination of light and heavy syllables, reflects the concept behind the modern binary notation of numbers used in computers. Earliest inscriptions (first centuries BCE and CE): numerals without decimal place value. See for instance how in the first column, 40 is formed byyp repeating the sy mbol for 20 twice. There is also no symbol for 0 and no mathematical concept of zero. • It is well established that so-called “Arabic numerals” originated in India. Their evolution has been traced to the Brâhmî script of MtiMauryan times. • The Webster dictionary gives the synonym of “Hindu-Arabic numeral”ls.” • All Indian numerals are also ultimately derived from Brâhmî numeral(ls (excep tfTt for Tamil ilhih, which had a different system using letters). Numbers 1 to 10 and symbolic connotations 0 - shunya bindu, kha, purna, vyoman, akasha, ambara, ananta… 1 - eka adi, pitamaha, tanu, kshiti, indu, soma, atman, brahman, surya… 2 - dvi ashvin, netra, paksha, yama... 3 - tri guna, loka, kala, agni, tripura, trishul, rama... 4 - chatur dish, yuga, irya, ashrama, veda... 5 - pañcha ishu, indriya, bhuta, pandava... 6 - shat rasa, anga, shanmukha, darshana... 7 - sapta ashva, naga, rishi, sagara, dvipa, buddha, sindhava, matrika... 8 - ashta gaja, naga, murti... 9 - nava anka, graha, chhidra, ratna... 10 - dasha anguli, asha, avatara, dish... Another example of the interface between science and spirituality in ancient India is found in the many names that numbers were given in scientific texts. Most of the names had philosophical or mythological backgrounds. The word râma,,, for instance, does not refer to Lord Rama but to number 3, because there were 3 Râmas (Parashurâma, Râma and Balarâma). Find out how many names you can explain in the above list. Indra’s Pearls Mathematical conceppgpygts are also found in the background of purely religious texts. The Avatamsaka Sûtra (a Buddhist text, a few centuries BCE), for instance, depicts a network of pearls placed in heavens by Indra so that “in each pearl one can see the reflections of all the others, as well as the reflections within the reflections and so on.” Three U.S. mathematicians found that Indra’s pearls follow the arrangement of circles in a “Schottky group” (and published a book entitled Indra’s Pearls). Two such structures are shown above. Of course, the Buddhist writers were unaware of these mathematical structures, but they seem to have had an intuition of the concept behind them. Modern science’s investigation of such ancient concepts is an interesting exercise. 4. Historical era: pre-Siddhantic astronomy The Rig-Veda clearly refers to an eclipse: the sun is struck with darkness by an asura (Svarbhânu). The eclipse was dated to 26 July 3928 BCE by P.C. Sengupta, but interpreting the texts to derive dates is always a delicate exercise. (Photo: annular solar eclipse of 15 January 2010 seen from Coimbatore) The above commentary on the Rig-Veda, by Sâyana, was composed in the 15th century and refers to an ancient tradition (“it is remembered”). With a yojana of 13.6 km (the yojana is sometimes defined as 8000 average human heights of 1.7m) and a nimesa of 16/75th of a second, this amounts to 280,755 km/s — just 6% from the speed of light (299,792 km/s).
Load more

Recommended publications
  • SARANATHAN COLLEGE of ENGINEERING (Approved by AICTE, New Delhi, Affiliated to Anna University, Chennai) Criterian 7.1.8
    SARANATHAN COLLEGE OF ENGINEERING (Approved by AICTE, New Delhi, Affiliated to Anna University, Chennai) Criterian 7.1.8 Institutional efforts/initiatives in providing an inclusive environment i.e., tolerance and harmony towards cultural, regional, linguistic, communal socioeconomic and other diversities Margazhi Mahothsavam For connoisseurs of Music and Dance, particularly classical, the month of Margazhi Dec- Jan period every year) is a much awaited month. It is even called as the music season. The music Sabhas and nowadays even the visual media conduct vocal and instrumental performances besides spiritual discourses much to the delight of the Rasikas. The celebrations have now been called “Margazhi Mahothsavam”. The Fine Arts club of our college, every year organizes a single day Mahothsavam in the month of December to showcase the talents of our students and staff members in Carnatic music and dance. It used to be an enjoyable evening highlighted by the august presence of awell-known legend in Trichy, in particular, in music, general and devotional. Pooja celebration Vijayadashami, is a major Indian festival celebrated on the tenth day of Ashvin month according to the Hindu calendar. This day falls in the month of September or October. The day culminates a 9-day fasting period of Navratri in the Hindu culture. It also coincides with immersion of the idol of Goddess Durga. The day is celebrated to commemorate the killing of Ravana by Lord Rama. The day also celebrates the killing of demon Mahishasur by Goddess Durga. Dussehra celebration spreads the message of the victory of good over evil. SaranathanCollege of Engineering celebrates Navarathri festival every year.
    [Show full text]
  • Khodiar Fire & Safety Equipments and Value Group 2012 Hindu
    Calendar Explanation ॐ वक्रतुं ड महाकाय कोटिसूययसमप्रभ टिटवयघ्िुं क रु मे देव सवयकायेष सवयदा॥ वटिष्ठ॥ यटममि ् पक्षे यत्र काले येि दृग्गटितै啍यम।् दृ�यते तेि पक्षेि क यायटिथ्याटदटििय म॥् भामकराचायय॥ यात्राटववाहोत्सवजातकादौ खेिैैः मफ िैरेवफलमफ ित्वम।् मयात्प्रो楍यते तेि िभश्चरािा ुं मफ िटक्रया दृग्गटितै啍यकृ द्या॥ We are pleased to release the 2012 calendar based on Hindu dharma shastra and drika siddhanta. This next day if you are in Japan, Fiji, Australia and other countries. For example if a total lunar eclipse is visible calendar is specially prepared for the Mumbai, India, and it may not be applicable in other parts of the world. in India at 5:00 AM it will happen on the previous day in the USA. For these reasons Indian Panchangam you bring from India cannot be used outside of India. People usually align the Hindu festivals with the English dates based on the Indian calendar. They think that nd if an Indian calendar says “Janmasthami” on a certain date, say September 2 2010, then it will appear as Uttarayana / Dakshinayana: The season occur based on earth’s position around the Sun. This is due to September 2nd everywhere in the world. The USA is 10:30 to 15:30 hours behind India, so some people will rd Earth’s tilt of 23.45 degrees. The Earth circles around Sun with this tilt. When the tilt is facing the Sun we get think it will also come the next day in the USA, i.e.
    [Show full text]
  • ICF Hindu Temple of Oklahoma Calendar of Events 2012 Vaishno Devi Temple
    ICF Hindu Temple of Oklahoma Calendar of Events 2012 Vaishno Devi Temple The first mention of the Mother Goddess is in the epic Mahabharat. When the armies of Pandavas and Kaurvas were arrayed in the battlefield of Kurukshetra, Arjun, the chief warrior of Pandavas upon the advice of Sri Krishna; meditated upon the Mother Goddess and sought Her bless- ings for victory. This is when Arjun addresses the Mother Goddess as ‘Jambookatak Chit- yaishu Nityam Sannihi- talaye’, which means ‘you who always dwell in the temple on the slope of the mountain in Jamboo’ (probably referring to the present day Jammu). Navratri Festival is cele- brated every year in Katra, the base camp of Sri Mata Vaishno Devi. On this auspicious occasion entire Katra town is decorated tastefully and people from the region participate in large numbers. In order to visit the Holy Shrine of Mata Vaishno Deviji, one has to reach Katra, a small town situated around 50 kms. from Jammu, the winter capi- tal of the state of Jammu & Kashmir. Katra serves as the base camp for the yatra. Katra is well connected to Jammu and Jammu, in turn, is well con- nected to the rest of the country by air, rail, and road. January 2012 Pushya - Magha Masa (Begins on 23rd ) Khara (Margazhi -Thai) (Dhanus - Makara) Sun Mon Tue Wed Thu Fri Sat 1 New Year 2 3 4 5 6 7 Muttangi Vaikuntha Ekadasi Sri Durga Pooja 6:30 PM Sri Venkateswara Seva 10:00 AM Pooja 6:30 PM Abhishekam 10:30 AM Ashtami 13:28:29 Navami 16:05:38 Dasami 18:42:43 Ekadasi 21:05:42 Dwadasi 23:03:17 Trayodasi 24:28:09 Chaturdasi 25:17:00
    [Show full text]
  • Cumulative Bio-Bibliography University of California, Santa Cruz June 2020
    Cumulative Bio-Bibliography University of California, Santa Cruz June 2020 Puragra Guhathakurta Astronomer/Professor University of California Observatories/University of California, Santa Cruz ACADEMIC HISTORY 1980–1983 B.Sc. in Physics (Honours), Chemistry, and Mathematics, St. Xavier’s College, University of Calcutta 1984–1985 M.Sc. in Physics, University of Calcutta Science College; transferred to Princeton University after first year of two-year program 1985–1987 M.A. in Astrophysical Sciences, Princeton University 1987–1989 Ph.D. in Astrophysical Sciences, Princeton University POSITIONS HELD 1989–1992 Member, Institute for Advanced Study, School of Natural Sciences 1992–1994 Hubble Fellow, Astrophysical Sciences, Princeton University 1994 Assistant Astronomer, Space Telescope Science Institute (UPD) 1994–1998 Assistant Astronomer/Assistant Professor, UCO/Lick Observatory, University of California, Santa Cruz 1998–2002 Associate Astronomer/Associate Professor, UCO/Lick Observatory, University of California, Santa Cruz 2002–2003 Herzberg Fellow, Herzberg Institute of Astrophysics, National Research Council of Canada, Victoria, BC, Canada 2002– Astronomer/Professor, UCO/Lick Observatory, University of California, Santa Cruz 2009– Faculty Director, Science Internship Program, University of California, Santa Cruz 2012–2018 Adjunct Faculty, Science Department, Castilleja School, Palo Alto, CA 2015 Visiting Faculty, Google Headquarters, Mountain View, CA 2015– Co-founder, Global SPHERE (STEM Programs for High-schoolers Engaging in Research
    [Show full text]
  • Satsang Sandesh a Monthly News Magazine Of
    Satsang Sandesh A monthly news magazine of India Temple Association, Inc. Hindu Temple, 25 E. Taunton Ave, Berlin, NJ 08009 SOUTH JERSEY ♦ DELAWARE ♦ PENNSYLVANIA Vol. 38 No. 2 Phone: (855) MYMANDIR (855-696-2634) www.indiatemple.org FEBRUARY 2012 MAHA SHIVRATRI CELEBRATION ON February 20, 2012 Abhishek of Lord Shiva from 9:00 am to 12:00 pm Also, there will be Rudrabhishek and Abhishek performed in the afternoon from 4:00 pm to 7:30 pm One of the most religious Hindu festivals, Maha Shivaratri falls on the fourteenth day of the dark fortnight of Phalguna (February- March), and is dedicated to the worship of Lord Shiva. Maha Shivratri is the night when He is said to have performed the Tandava Nritya or the dance of pri- mordial creation, preservation and destruction. The festival is observed for one day and one night only. Maha Shivratri is universally observed by all pious Hindus with fasting, singing of bhajans, recital of Sanskrit shlokas, offering of prayers, flowers, fruits and food that is specially prepared in honor of the deity and his divine consort, goddess Parvati. The Puranas contain many stories and legends describing the origin of this festival. According to one, during the samudra manthan, Religious Calendar a pot of poison emerged from the ocean. This terrified the Gods and demons as the poison was capable of destroying the entire world, and they ran to Shiva for help. To protect the world from Feb 3, Friday its evil effects, Shiva drank the deathly poison but held it in his throat instead of swallowing it.
    [Show full text]
  • Essence of Hindu Festivals & Austerities
    ESSENCE OF HINDU FESTIVALS AND AUSTERITIES Edited and translated by V.D.N.Rao, former General Manager of India Trade Promotion Organization, Ministry of Commerce, Govt. of India, Pragati Maidan, New Delhi now at Chennai 1 Other Scripts by the same Author: Essence of Puranas:- Maha Bhagavata, Vishnu Purana, Matsya Purana, Varaha Purana, Kurma Purana, Vamana Purana, Narada Purana, Padma Purana; Shiva Purana, Linga Purana, Skanda Purana, Markandeya Purana, Devi Bhagavata;Brahma Purana, Brahma Vaivarta Purana, Agni Purana, Bhavishya Purana, Nilamata Purana; Shri Kamakshi Vilasa Dwadasha Divya Sahasranaama: a) Devi Chaturvidha Sahasra naama: Lakshmi, Lalitha, Saraswati, Gayatri; b) Chaturvidha Shiva Sahasra naama-Linga-Shiva-Brahma Puranas and Maha Bhagavata; c) Trividha Vishnu and Yugala Radha-Krishna Sahasra naama-Padma-Skanda-Maha Bharata and Narada Purana. Stotra Kavacha- A Shield of Prayers Purana Saaraamsha; Select Stories from Puranas Essence of Dharma Sindhu Essence of Shiva Sahasra Lingarchana Essence of Paraashara Smtiti Essence of Pradhana Tirtha Mahima Dharma Bindu Essence of Upanishads : Brihadaranyaka , Katha, Tittiriya, Isha, Svetashwara of Yajur Veda- Chhandogya and Kena of Saama Veda-Atreya and Kausheetaki of Rig Veda-Mundaka, Mandukya and Prashna of Atharva Veda ; Also ‘Upanishad Saaraamsa’ (Quintessence of Upanishads) Essence of Virat Parva of Maha Bharata Essence of Bharat Yatra Smriti Essence of Brahma Sutras* Essence of Sankhya Parijnaana*- Also Essence of Knowledge of Numbers Essence of Narada Charitra Essence Neeti Chandrika* [Note: All the above Scriptures already released on www. Kamakoti. Org/news as also on Google by the respective references. The one with * is under process] 2 PREFACE Dharma and Adharma are the two wheels of Life‟s Chariot pulling against each other.
    [Show full text]
  • Trade Marks Journal No: 1955 , 06/07/2020 Class 36 2744791 27
    Trade Marks Journal No: 1955 , 06/07/2020 Class 36 2744791 27/05/2014 THE PRUDENTIAL INSURANCE COMPANY OF AMERICA 751 BROAD STREET, NEWARK, NEW JERSEY 07102, UNITED STATES OF AMERICA. SERVICE PROVIDERS ( A CORPORATION DULY ORGANISED AND EXISTING UNDER THE LAWS OF THE STATE OF NEW JERSEY, U. S. A. ) Address for service in India/Attorney address: LALL & SETHI D-17, N.D.S.E.-II NEW DELHI-49 Proposed to be Used DELHI INSURANCE; FINANCIAL AFFAIRS; MONETARY AFFAIRS; REAL ESTATE AFFAIRS 5128 Trade Marks Journal No: 1955 , 06/07/2020 Class 36 VR KOLKATTA 2833314 28/10/2014 VR ASSET MANAGEMENT PTE. LTD. 10 MARINA BOULEVARD, #16-03, MARINA BAY FINANCIAL CENTRE, SINGAPORE (018983) SERVICE PROVIDER Address for service in India/Attorney address: SARC ASSOCIATES PVT. LTD 129, DDA SITE-1, NEW RAJINDER NAGAR, NEW DELHI-60 Used Since :17/09/2011 DELHI INSURANCE, FINANCIAL AFFAIRS; MONETARY AFFAIRS REAL ESTATE AFFAIRS Registration of this trade mark shall give no right to the exclusive use of the word KOLKATTA.. 5129 Trade Marks Journal No: 1955 , 06/07/2020 Class 36 2999301 03/07/2015 TATA AIA LIFE INSURANCE COMPANY LTD. 14TH FLOOR, TOWER A, PENINSULA BUSINESS PARK, SENAPATI BAPAT MARG, LOWER PAREL, MUMBAI-400013 SERVICE PROVIDERS AN INDIAN COMPANY INCORPORATED UNDER THE COMPANIES ACT Address for service in India/Agents address: KRISHNA & SAURASTRI. 74 - F, VENUS, WORLI SEA FACE, MUMBAI - 400 018. Used Since :23/08/2000 MUMBAI INSURANCE, LIFE AND NON LIFE INSURANCE, HEALTHCARE INSURANCE UNDERWRITING, LIFE INSURANCE UNDERWRITING, INSURANCE CONSULTANCY, INSURANCE BROKERAGE, FINANCIAL PLANNING EVALUATION, INSURANCE INFORMATION REGISTRATION OF THIS TRADE MARK SHALL GIVE NO RIGHT TO THE EXCLUSIVE USE OF THE WORDS SMART INSURE EXCEPT SUBSTANTIALLY AS SHOWN IN THE REPRESENTATION ON THE FORM OF APPLICATION.
    [Show full text]
  • Proposal Shreee Salasar Balaji Rajasthan
    Dear Sir, About Salasar Dham:- Salasar Balaji or Salasar Dham is a place of religious importance for the devotees of Lord Hanumana. It is located in the town of Salasar, on NH-65 near Sujangarh in Churu district, Rajasthan. It is located near the pilgrim centers of Rani Sati Temple and Khatushyamji. The temple of Balaji which is another name of Hanuman is situated in the middle of Salasar and attracts innumerable worshippers throughout the year especially on Chaitra Purnima and Ashvin Purnima. The temple of Salasar Balaji is now considered to be a Shakti Sthal (a place of power) and Swayambhu (self creation) by faith, belief, miracles and wish fulfillments of the devotees. The idol of Balaji here is different from all other idols of Lord Hanumana. Hanumana possess round face with moustache and beard making it the most unique idol among the other idols of Hanumana all over the world. Highlights of the Salasar Dham:- Some of the regular activities of the temple which is very touching as per devotees values and social beliefs. • Regular worships of the deity. • Performing Aarti on fixed time slots. • Feasting of Brahmins and other mendicants. • Recitation of Ramayana . • Recitation of Kirtan & Bhajans . • Arrangement for Savamanis. • Recitation of Sundar Kand on every Tuesday in union by the singers. • Arrangement of stay for the visitors. • Even Regular Visit of Celebrities on monthly basis like Navjyot Singh Siddhu, Lakhbir Singh Lakkha, Swami Avdheshanand Giri ji Maharaj, Sanjay Dutt, Nisha Kothari etc. While the worship of the deity is managed by the Brahmins priests from the Dadhich clan, the temple is managed and maintained by the trust Hanuman Sewa Samiti.
    [Show full text]
  • Hindu Festivals
    Hindu Festivals What makes Hindus different is that they honor the whole of creation and see the presence of God in everything. Everyone has a right to evolve spiritually and will release the Truth in due course. Hinduism* is very liberal and does not set limits for mankind. There are many lives and many lifetimes but each are guided by the strict Law of Karma where man is responsible for every action he performs . This is aptly describe by Apollonius Tyanaeus over 2000 years ago (Greek Philosopher) “In India I found a race of mortals living upon the Earth, but not adhering to it, inhabiting cities, but not being fixed to them, possessing everything, but possessed by nothing.” November 5th, 2017, 1 to 4:30 p.m. 130 Westmore Drive, Unit 9, Etobicoke, Ontario Hindu festivals follow the Vikrami Lunar calendar. A month has two fortnight called paksha. One fortnight is the bright or waxing fortnight where the moon grows in size and ends with the full moon and the other is the dark or waning fortnight that ends in new moon. The months do not exactly match the Gregorian calendar so exact dates will not be given here, only an approximation. GANGUAR GAURI FAST is observed by married women (to enhance the love of their husbands) and unmarried girls (to get good husbands). This fast is observed in the month of Chaitra (March/April) for 17 days from the first day of the dark fortnight (Krishna Paksha) CHAITRA NAVRATRI starts on the first day on the bright fortnight in Chaitra and goes for nine nights.
    [Show full text]
  • Digital Hsgc-2020-Calendar-C
    Hindu Temple of Greater Cincinnati Phone: 513-528-3714 January 2020 Paush/Maagh, Vikram Samvat 2076 Sunday Monday Tuesday Wednesday Thursday Friday Saturday January Events 1* 2 3 4 * New Year’s Day - Havan 11am Thai Pongal & its Celebration Temple Open All Day Vishnu Sahasranam VenkateswaraPooja Navagrah Pooja *Temple open 9am to 8pm Swami Vivekanand Jayanti New Year’s Day Parayan 7pm 7pm 3 pm Mata Ki Chouki Republic Day of India Mataki Chouki 4pm Lohri Vasant Panchami Havan 11am Sai Bhajan 6pm Uttarayan Punyakal - Makarsankranti Paush Shukla 6 7 8 9 Pradosh 5 6 7 128 9 10 11 Sunderkand Path Shiv Abhishek Hanuman Chalisa Purushottam Vishnu Sahasranam VenkateswaraPooja 10:30am Shiv Mahiman 6:45pm Sahasranam Stotram Parayan 7pm 7pm Stotram 6:45pm SatyaNarayan Pooja Parayan 6pm Paush Shukla 11 6:30pm Vaikuntha Ekadashi Paush| Maagh 10 12: Mukkoti Dwadashi 13 Paush Shukla 15 Putrada Ekadashi 14 Krishna 1 Purnima 12 13 Lohri 14 15 16 1 7 18 5/6 1008 Gayatri Japam Shiv Abhishek Thai Pongal Vishnu Sahasranam Swami Vivekanand 9:30am Shiv Mahiman Parayan 7pm Jayanti Pooja 6pm Uttarayana: Stotram Hanuman Chalisa Punyakal Venkateswara Pooja Sankashti Chaturthi 6:45pm Makar Sankranti 7pm Pooja 6pm 2 3/4: Sankashti 7 Chaturthi 4 5/6 8 9 19 20 21 22 Pradosh 23 24 25 Thai Pongal M. L. King’s Day Hanuman Chalisa Vishnu Sahasranam VenkateswaraPooja Venkateswara 6:45pm Parayan 7pm 7pm Abhishekam 10am Celebration Shiv Abhishek Murugan Shiv Mahiman Stotram 6:45pm Paush/ Maagh Abhishekam10:30am Paush| Maagh Krishna Krishna 30 Maagh Shukla 1 10 11: Shatila
    [Show full text]
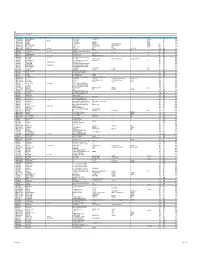
  • Details of Shareholders Unclaimed
    HCC CONSECUTIVE OUTSTANDING PHY AND ELC RECORDS DIV PAY DATE 14-06-2011 SrNo Folio No/DPID ClientID 1st Holder Name 1st Joint Holder 2nd Joint Holder Add Line 1 Add Line 2 Add Line 3 Add Line 4 Add State Add Pincode Cumrrent Holding Amount_14JUN11 1 1201320000260366 SHIRODE ASHABAI VAMAN AT POST - SAYGAON TAL. CHALISGAON JALGAON 100 40.00 2 1203450000046694 MANISHA DANA Suvajit Dana B-1/135, KALYANI, NADIA 50 20.00 3 1201130000108840 ANITA MODI 410, A SILVER MALL, 8, RNT MARG, INDORE 40 16.00 4 1206850000006279 VIBHA RANGA W/O RAJESH RANGA KARMISAR ROAD OUT SIDE NATHUSAR GATE BIKANER 33401 40 16.00 5 1201060100100743 AMRISH NARESH SAXENA H. NO. 17 KABIR NIWAS MGIMS CAMPUS, SEWAGRAM WARDHA 42102 420 114.40 6 1201060100048428 Manoj Kumar Yadav Subhama Vihar Colony Lafagarh Gas , Godam Mangla Bilaspur 47751 100 40.00 7 IN30023910776917 RAHUL DUGGAL Shaveta Kapoor 15TH FLOOR SMSD PO BOX 3838 ABUDHABI, UAE 100000 600 240.00 8 IN30023911246780 OTTAKATH CHATHUNTAKAYIL KUTTIAMU P O BOX 61999 ABUDHABI U A E U A E 100000 600 240.00 9 HKA0009149 ASHOK KUMAR GULANI Padmaja Gulani 4/2 SINGLE STOREY RAMESH NAGAR NEW DELHI 110001 1000 400.00 10 HKB0040862 B S YADAV EDUCATION JCO HQ 502 AD GP (SP) C/O 56 APO DELHI 110001 500 400.00 11 HKC0264587 COLOMPRAKASH AWASTHY 11 CORPS PROVOST UNIT C/O 56 APO DELHI 110001 250 200.00 12 HKD0255276 DIPANKAR BANERJEE Sandhya Banerjee IDSA SAPRU HOUSE BARAKHAMBA ROAD NEW DELHI 110001 1500 1,200.00 13 HKK0006845 KARUNA SHARMA Raman Kumar H NO D-2 RANA PARTAP BAGH G T ROAD DELHI 110001 1000 800.00 14 HKN0259201 NEERJA
    [Show full text]
  • Ulhi ,Qgxvwuldo 3Uriloh Ri 'Lvwulfw
    Brief Industrial Profile of District Ashoknagar Madhya Pradesh Carried out by MSME -Development Institute, Indore (MP) (Ministry of MSME, Govt. of India,) Phone 0731 2421659, 2421037 Fax: 0731 2420723, 2421540 E-mail: [email protected] Web- www.msmeindore.nic.in Contents S. No. Topic Page No. 1. General Characteristics of the District 02 1.1 Location & Geographical Area 02 – 03 1.2 Topography 03 1.3 Availability of Minerals. 03 1.4 Forest 04 1.5 Administrative set up 04 2. District at a glance 04 – 06 2.1 Existing Status of Industrial Area in the District Ashoknagar 06 3. Industrial Scenario Of Ashoknagar 06 3.1 Industry at a Glance 06 – 07 3.2 Year Wise Trend Of Units Registered 07 3.3 Details Of Existing Micro & Small Enterprises & Artisan Units In 07 – 08 The District 3.4 Large Scale Industries / Public Sector undertakings 08 3.5 Major Exportable Item 08 3.6 Growth Trend 08 3.7 Vendorisation / Ancillarisation of the Industry 08 3.8 Medium Scale Enterprises 08 3.9 Service Enterprises 09 3.9.1 Potentials areas for service industry 09 3.10 Potential for new MSMEs 09 4. Existing Clusters of Micro & Small Enterprise 09 4.1 Detail Of Major Clusters 09 – 10 4.1.1 Manufacturing Sector 10 4.1.2 Service Sector 11 4.2 Details of Identified cluster 11 4.2.1 Chanderi Saree Cluster 11 – 12 5. General issues raised by industry association during the course of 12 meeting 6 Steps to set up MSMEs 13 1 Brief Industrial Profile of Ashoknagar District 1.
    [Show full text]