Hyperbolic Metrics, Measured Foliations and Pants Decompositions for Non-Orientable Surfaces Athanase Papadopoulos, Robert C
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TRANSVERSE STRUCTURE of LIE FOLIATIONS 0. Introduction This
TRANSVERSE STRUCTURE OF LIE FOLIATIONS BLAS HERRERA, MIQUEL LLABRES´ AND A. REVENTOS´ Abstract. We study if two non isomorphic Lie algebras can appear as trans- verse algebras to the same Lie foliation. In particular we prove a quite sur- prising result: every Lie G-flow of codimension 3 on a compact manifold, with basic dimension 1, is transversely modeled on one, two or countable many Lie algebras. We also solve an open question stated in [GR91] about the realiza- tion of the three dimensional Lie algebras as transverse algebras to Lie flows on a compact manifold. 0. Introduction This paper deals with the problem of the realization of a given Lie algebra as transverse algebra to a Lie foliation on a compact manifold. Lie foliations have been studied by several authors (cf. [KAH86], [KAN91], [Fed71], [Mas], [Ton88]). The importance of this study was increased by the fact that they arise naturally in Molino’s classification of Riemannian foliations (cf. [Mol82]). To each Lie foliation are associated two Lie algebras, the Lie algebra G of the Lie group on which the foliation is modeled and the structural Lie algebra H. The latter algebra is the Lie algebra of the Lie foliation F restricted to the clousure of any one of its leaves. In particular, it is a subalgebra of G. We remark that although H is canonically associated to F, G is not. Thus two interesting problems are naturally posed: the realization problem and the change problem. The realization problem is to know which pairs of Lie algebras (G, H), with H subalgebra of G, can arise as transverse and structural Lie algebras, respectively, of a Lie foliation F on a compact manifold M. -

Foliations Transverse to Fibers of a Bundle
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 42, Number 2, February 1974 FOLIATIONS TRANSVERSE TO FIBERS OF A BUNDLE J. F. PLANTE Abstract. Consider a fiber bundle where the base space and total space are compact, connected, oriented smooth manifolds and the projection map is smooth. It is shown that if the fiber is null-homologous in the total space, then the existence of a foliation of the total space which is transverse to each fiber and such that each leaf has the same dimension as the base implies that the fundamental group of the base space has exponential growth. Introduction. Let (E, p, B) be a locally trivial fiber bundle where /»:£-*-/? is the projection, E and B are compact, connected, oriented smooth manifolds and p is a smooth map. (By smooth we mean C for some r^l and, henceforth, all maps are assumed smooth.) Let b denote the dimension of B and k denote the dimension of the fiber (thus, dim E= b+k). By a section of the fibration we mean a smooth map a:B-+E such that p o a=idB. It is well known that if a section exists then the fiber over any point in B represents a nontrivial element in Hk(E; Z) since the image of a section is a compact orientable manifold which has intersection number one with the fiber over any point in B. The notion of a section may be generalized as follows. Definition. A polysection of (E,p,B) is a covering projection tr:B-*B together with a map Ç:B-*E such that the following diagram commutes. -

FOLIATIONS Introduction. the Study of Foliations on Manifolds Has a Long
BULLETIN OF THE AMERICAN MATHEMATICAL SOCIETY Volume 80, Number 3, May 1974 FOLIATIONS BY H. BLAINE LAWSON, JR.1 TABLE OF CONTENTS 1. Definitions and general examples. 2. Foliations of dimension-one. 3. Higher dimensional foliations; integrability criteria. 4. Foliations of codimension-one; existence theorems. 5. Notions of equivalence; foliated cobordism groups. 6. The general theory; classifying spaces and characteristic classes for foliations. 7. Results on open manifolds; the classification theory of Gromov-Haefliger-Phillips. 8. Results on closed manifolds; questions of compact leaves and stability. Introduction. The study of foliations on manifolds has a long history in mathematics, even though it did not emerge as a distinct field until the appearance in the 1940's of the work of Ehresmann and Reeb. Since that time, the subject has enjoyed a rapid development, and, at the moment, it is the focus of a great deal of research activity. The purpose of this article is to provide an introduction to the subject and present a picture of the field as it is currently evolving. The treatment will by no means be exhaustive. My original objective was merely to summarize some recent developments in the specialized study of codimension-one foliations on compact manifolds. However, somewhere in the writing I succumbed to the temptation to continue on to interesting, related topics. The end product is essentially a general survey of new results in the field with, of course, the customary bias for areas of personal interest to the author. Since such articles are not written for the specialist, I have spent some time in introducing and motivating the subject. -

Lecture Notes on Foliation Theory
INDIAN INSTITUTE OF TECHNOLOGY BOMBAY Department of Mathematics Seminar Lectures on Foliation Theory 1 : FALL 2008 Lecture 1 Basic requirements for this Seminar Series: Familiarity with the notion of differential manifold, submersion, vector bundles. 1 Some Examples Let us begin with some examples: m d m−d (1) Write R = R × R . As we know this is one of the several cartesian product m decomposition of R . Via the second projection, this can also be thought of as a ‘trivial m−d vector bundle’ of rank d over R . This also gives the trivial example of a codim. d- n d foliation of R , as a decomposition into d-dimensional leaves R × {y} as y varies over m−d R . (2) A little more generally, we may consider any two manifolds M, N and a submersion f : M → N. Here M can be written as a disjoint union of fibres of f each one is a submanifold of dimension equal to dim M − dim N = d. We say f is a submersion of M of codimension d. The manifold structure for the fibres comes from an atlas for M via the surjective form of implicit function theorem since dfp : TpM → Tf(p)N is surjective at every point of M. We would like to consider this description also as a codim d foliation. However, this is also too simple minded one and hence we would call them simple foliations. If the fibres of the submersion are connected as well, then we call it strictly simple. (3) Kronecker Foliation of a Torus Let us now consider something non trivial. -

Commentary on Thurston's Work on Foliations
COMMENTARY ON FOLIATIONS* Quoting Thurston's definition of foliation [F11]. \Given a large supply of some sort of fabric, what kinds of manifolds can be made from it, in a way that the patterns match up along the seams? This is a very general question, which has been studied by diverse means in differential topology and differential geometry. ... A foliation is a manifold made out of striped fabric - with infintely thin stripes, having no space between them. The complete stripes, or leaves, of the foliation are submanifolds; if the leaves have codimension k, the foliation is called a codimension k foliation. In order that a manifold admit a codimension- k foliation, it must have a plane field of dimension (n − k)." Such a foliation is called an (n − k)-dimensional foliation. The first definitive result in the subject, the so called Frobenius integrability theorem [Fr], concerns a necessary and sufficient condition for a plane field to be the tangent field of a foliation. See [Spi] Chapter 6 for a modern treatment. As Frobenius himself notes [Sa], a first proof was given by Deahna [De]. While this work was published in 1840, it took another hundred years before a geometric/topological theory of foliations was introduced. This was pioneered by Ehresmann and Reeb in a series of Comptes Rendus papers starting with [ER] that was quickly followed by Reeb's foundational 1948 thesis [Re1]. See Haefliger [Ha4] for a detailed account of developments in this period. Reeb [Re1] himself notes that the 1-dimensional theory had already undergone considerable development through the work of Poincare [P], Bendixson [Be], Kaplan [Ka] and others. -
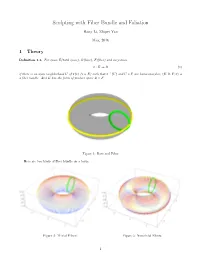
Sculpting with Fiber Bundle and Foliation
Sculpting with Fiber Bundle and Foliation Hang Li, Zhipei Yan May, 2016 1 Theory Definition 1.1. For space E(total space), B(base), F (fiber) and surjection π : E ! B (1) if there is an open neighborhood U of π(x) (x 2 E) such that π−1(U) and U × F are homeomorphic, (E; B; F; π) is a fiber bundle. And E has the form of product space B × F . Figure 1: Base and Fiber Here are two kinds of fiber bundle on a torus. Figure 2: Trivial Fibers Figure 3: Nontrivial Fibers 1 Definition 1.2. fUig is an atlas of an n-dimensional manifold U. For each chart Ui, define n φi : Ui ! R (2) If Ui \ Uj 6= ;, define −1 'ij = φj ◦ φi (3) And if 'ij has the form of 1 2 'ij = ('ij(x);'ij(x; y)) (4) 1 n−p n−p 'ij : R ! R (5) 2 n p 'ij : R ! R (6) then for any stripe si : x = ci in Ui there must be a stripe in Uj sj : x = cj such that si and sj are the same curve in Ui \ Uj and can be connected. The maximal connection is a leaf. This structure is called a p-dimensional foliation F of an n-dimensional manifold U. Property 1.1. All the fiber bundles compose a group GF = (fFig; ◦). If we regard the fiber bundle(1-manifold) as a parameterization on a surface(2-manifold), we can prove it easily. As an example, we use the parameterization on a torus. -

On the First Homology of the Groups of Foliation Preserving Diffeomorphisms for Foliations with Singularities of Morse Type
Publ. RIMS, Kyoto Univ. 44 (2008), 1057–1068 On the First Homology of the Groups of Foliation Preserving Diffeomorphisms for Foliations with Singularities of Morse Type By Kazuhiko Fukui∗ Abstract n Let R be an n-dimensional Euclidean space and Fϕ be the foliation defined by levels of a Morse function ϕ : Rn → R. We determine the first homology of n the identity component of the foliation preserving diffeomorphism group of (R , Fϕ). Then we can apply it to the calculation of the first homology of the foliation preserving diffeomorphism groups for codimension one compact foliations with singularities of Morse type. §1. Introduction and Statement of Results Let F be a C∞-foliation (with or without singularities) on a C∞-manifold M.LetD∞(M,F) denote the group of all foliation preserving C∞- diffeomorphisms of (M,F) which are isotopic to the identity through folia- tion preserving C∞-diffeomorphisms with compact support. In [2], we have studied the structure of the first homology of D∞(M,F) for compact Haus- dorff foliations F, and we have that it describes the holonomy structures of isolated singular leaves of F. Here the first homology group H1(G) of a group G is defined as the quotient of G by its commutator subgroup. In this paper we treat the foliation preserving C∞-diffeomorphism groups for codimension one foliations with singularities. Communicated by K. Saito. Received February 7, 2007. Revised October 22, 2007. This research was partially supported by Grant-in-Aid for Scientific Research (No. 17540098), Japan Society for the Promotion of Science. -

Types of Integrability on a Submanifold and Generalizations of Gordon’S Theorem
Trudy Moskov. Matem. Obw. Trans. Moscow Math. Soc. Tom 66 (2005) 2005, Pages 169–241 S 0077-1554(05)00149-4 Article electronically published on November 9, 2005 TYPES OF INTEGRABILITY ON A SUBMANIFOLD AND GENERALIZATIONS OF GORDON’S THEOREM N. N. NEKHOROSHEV Abstract. At the beginning of the paper the concept of Liouville integrability is analysed for systems of general form, that is, ones that are not necessarily Hamil- tonian. On this simple basis Hamiltonian systems are studied that are integrable only on submanifolds N of the phase space, which is the main subject of the paper. The study is carried out in terms of k-dimensional foliations and fibrations defined on N by the Hamiltonian vector fields corresponding to k integrals in involution. These integrals are said to be central and may include the Hamiltonian function of the system. The parallel language of sets of functions is also used, in particular, sets of functions whose common level surfaces are the fibres of fibrations. Relations between different types of integrability on submanifolds of the phase space are established. The main result of the paper is a generalization of Gordon’s theorem stating that in a Hamiltonian system all of whose trajectories are closed the period of the solutions depends only on the value of the Hamiltonian. Our generalization asserts that in the case of the strongest “Hamiltonian” integrability the frequencies of a conditionally periodic motion on the invariant isotropic tori that form a fibration of an integrability submanifold depend only on the values of the central integrals. Under essentially weaker assumptions on the fibration of the submanifold into such tori it is proved that the circular action functions also have the same property. -

Foliations and Spinnable Structures on Manifolds Annales De L’Institut Fourier, Tome 23, No 2 (1973), P
ANNALES DE L’INSTITUT FOURIER ITIRO TAMURA Foliations and spinnable structures on manifolds Annales de l’institut Fourier, tome 23, no 2 (1973), p. 197-214 <http://www.numdam.org/item?id=AIF_1973__23_2_197_0> © Annales de l’institut Fourier, 1973, tous droits réservés. L’accès aux archives de la revue « Annales de l’institut Fourier » (http://annalif.ujf-grenoble.fr/) implique l’accord avec les conditions gé- nérales d’utilisation (http://www.numdam.org/conditions). Toute utilisa- tion commerciale ou impression systématique est constitutive d’une in- fraction pénale. Toute copie ou impression de ce fichier doit conte- nir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ Ann. Inst. Fourier, Grenoble 23, 2 (1973), 197-214. FOLIATIONS AND SPINNABLE STRUCTURES ON MANIFOLDS by Itiro TAMURA Introduction. In a previous paper, it was shown by using the methods of differential topology that every odd dimensional sphere has a codimension-one foliatiojn (Tamura [12]). This result and the techniques used there, are powerful tools in carrying out the construction of codimension-one foliations for compact odd dimensional differentiable manifolds. In this paper the concept of a spinnable structure on a differentiable manifold is introduced in order to clarify the implication of the differential topological arguments mentioned above (see Definition 1). Roughly speaking, a differentiable manifold is spinnable if it can spin around an axis as if the top spins. The choice of axes of spinnable structures is essential for constructing a codimension-one foliation. For example, the existence of a codimension-one foliation follows from the existence of a spinnable structure having an odd dimensional sphere a.s axis (see Theorem 5). -

Integral Formulas for a Foliation with a Unit Normal Vector Field
mathematics Article Integral Formulas for a Foliation with a Unit Normal Vector Field Vladimir Rovenski Department of Mathematics, University of Haifa, Mount Carmel, Haifa 3498838, Israel; [email protected] Abstract: In this article, we prove integral formulas for a Riemannian manifold equipped with a foliation F and a unit vector field N orthogonal to F, and generalize known integral formulas (due to Brito-Langevin-Rosenberg and Andrzejewski-Walczak) for foliations of codimension one. Our integral formulas involve Newton transformations of the shape operator of F with respect to N and the curvature tensor of the induced connection on the distribution D = TF ⊕ span(N), and this decomposition of D can be regarded as a codimension-one foliation of a sub-Riemannian manifold. We apply our formulas to foliated (sub-)Riemannian manifolds with restrictions on the curvature and extrinsic geometry of the foliation. Keywords: Riemannian manifold; foliation; harmonic distribution; Newton transformation; shape operator; r-th mean curvature MSC: 53C12; 53C17 1. Introduction Foliations, which are defined as partitions of a manifold into collections of submani- Citation: Rovenski, V. Integral folds of the same dimension, called leaves, appeared in the 1940s in the works of G. Reeb Formulas for a Foliation with a Unit and Ch. Ehresmann, culminating in the book [1]. Since then, the subject has enjoyed a Normal Vector Field. Mathematics rapid development, see e.g., [2]. Extrinsic geometry of foliations of Riemannian manifolds 2021, 9, 1764. https://doi.org/ 10.3390/math9151764 was developed in recent years, see surveys in [3–9], and has applications in differential geometry and analysis on real and complex manifolds. -

Geometry of Foliated Manifolds
E extracta mathematicae Vol. 31, N´um.2, 189 { 197 (2016) Geometry of Foliated Manifolds A.Ya. Narmanov, A.S. Sharipov Namangan Engineering-Pedagogical Institute, Namangan National University of Uzbekistan, Tashkent, Uzbekistan [email protected] , [email protected] Presented by Manuel de Le´on Received March 15, 2016 Abstract: In this paper some results of the authors on geometry of foliated manifolds are stated and results on geometry of Riemannian (metric) foliations are discussed. Key words: Foliation, foliated manifold, Riemannian submersion, Riemannian foliation, Gaussian curvature. AMS Subject Class. (2010): 53C12, 57C30. 1. Introduction A manifold, with some fixed foliation on it, is called a foliated manifold. Theory of foliated manifolds is one of new fields of mathematics. It appeared in the intersection of Differential Equations, Differential Geometry and Dif- ferential Topology in the second part of 20th century. In formation and development of the theory of foliations the big contribu- tion was made by famous mathematicians such as C. Ehresmann [1], G. Reeb [15], A. Haefliger [3], R. Langevin [8], C. Lamoureux [7]. Further development of the geometrical theory of foliations is connected with known works of R. Hermann [4, 5], P. Molino [9], B.L. Reinhart [16], Ph. Tondeur [17]. At present, the theory of foliations (the theory of foliated manifolds) is intensively developing and has wide applications in many fields of science and technique. In the theory of foliations, it is possible to get acquainted with the latest scientific works in work Ph. Tondeur [18], where the bibliography consisting of more than 2500 works on the theory of foliations is provided. -

On Equivalent Lie Foliations
Journal of Pure and Applied Mathematics: Advances and Applications Volume 20, Number 1, 2019, Pages 31-39 Available at http://scientificadvances.co.in DOI: http://dx.doi.org/10.18642/jpamaa_7100122009 ON EQUIVALENT LIE FOLIATIONS AMETH NDIAYE Départment de Mathématiques (FASTEF) Université Cheikh Anta Diop Dakar Senegal e-mail: [email protected] Abstract In this paper we study in which condition two Lie foliations are equivalent. In particular, our foliations are defined by the orbit of a group action on a compact manifold. Every manifold in this paper is compact and our Lie group G is connected and simply connected. 1. Introduction Let G be a simply connected Lie group and M be a compact manifold of dimension n. A Lie G-foliation is the given of a set F of couples ()U; f , where U is an open subset of M and f : U → G a submersion, having the following properties: 2010 Mathematics Subject Classification: Primary 53B05; Secondary 53B20. Keywords and phrases: foliation, nilpotent, Lie group, action group, manifold, compact. Received September 27, 2018 2019 Scientific Advances Publishers This work is licensed under the Creative Commons Attribution International License (CC BY 3.0). http://creativecommons.org/licenses/by/3.0/deed.en_US 32 AMETH NDIAYE (i) The open sets U cover M. (ii) for all ()U; f and (W; h) ∈ F , there exists g ∈ G such that, for all x ∈ U ∩ W, we have f (x) = h(x)g. In particular, level surfaces of the submersions f, for (U; f ) ∈ F , recollect to form a Lie foliation on M.