Functional Languages
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Functional Programming Is Style of Programming in Which the Basic Method of Computation Is the Application of Functions to Arguments;
PROGRAMMING IN HASKELL Chapter 1 - Introduction 0 What is a Functional Language? Opinions differ, and it is difficult to give a precise definition, but generally speaking: • Functional programming is style of programming in which the basic method of computation is the application of functions to arguments; • A functional language is one that supports and encourages the functional style. 1 Example Summing the integers 1 to 10 in Java: int total = 0; for (int i = 1; i 10; i++) total = total + i; The computation method is variable assignment. 2 Example Summing the integers 1 to 10 in Haskell: sum [1..10] The computation method is function application. 3 Historical Background 1930s: Alonzo Church develops the lambda calculus, a simple but powerful theory of functions. 4 Historical Background 1950s: John McCarthy develops Lisp, the first functional language, with some influences from the lambda calculus, but retaining variable assignments. 5 Historical Background 1960s: Peter Landin develops ISWIM, the first pure functional language, based strongly on the lambda calculus, with no assignments. 6 Historical Background 1970s: John Backus develops FP, a functional language that emphasizes higher-order functions and reasoning about programs. 7 Historical Background 1970s: Robin Milner and others develop ML, the first modern functional language, which introduced type inference and polymorphic types. 8 Historical Background 1970s - 1980s: David Turner develops a number of lazy functional languages, culminating in the Miranda system. 9 Historical Background 1987: An international committee starts the development of Haskell, a standard lazy functional language. 10 Historical Background 1990s: Phil Wadler and others develop type classes and monads, two of the main innovations of Haskell. -

Comparative Studies of Programming Languages; Course Lecture Notes
Comparative Studies of Programming Languages, COMP6411 Lecture Notes, Revision 1.9 Joey Paquet Serguei A. Mokhov (Eds.) August 5, 2010 arXiv:1007.2123v6 [cs.PL] 4 Aug 2010 2 Preface Lecture notes for the Comparative Studies of Programming Languages course, COMP6411, taught at the Department of Computer Science and Software Engineering, Faculty of Engineering and Computer Science, Concordia University, Montreal, QC, Canada. These notes include a compiled book of primarily related articles from the Wikipedia, the Free Encyclopedia [24], as well as Comparative Programming Languages book [7] and other resources, including our own. The original notes were compiled by Dr. Paquet [14] 3 4 Contents 1 Brief History and Genealogy of Programming Languages 7 1.1 Introduction . 7 1.1.1 Subreferences . 7 1.2 History . 7 1.2.1 Pre-computer era . 7 1.2.2 Subreferences . 8 1.2.3 Early computer era . 8 1.2.4 Subreferences . 8 1.2.5 Modern/Structured programming languages . 9 1.3 References . 19 2 Programming Paradigms 21 2.1 Introduction . 21 2.2 History . 21 2.2.1 Low-level: binary, assembly . 21 2.2.2 Procedural programming . 22 2.2.3 Object-oriented programming . 23 2.2.4 Declarative programming . 27 3 Program Evaluation 33 3.1 Program analysis and translation phases . 33 3.1.1 Front end . 33 3.1.2 Back end . 34 3.2 Compilation vs. interpretation . 34 3.2.1 Compilation . 34 3.2.2 Interpretation . 36 3.2.3 Subreferences . 37 3.3 Type System . 38 3.3.1 Type checking . 38 3.4 Memory management . -

Lisp: Final Thoughts
20 Lisp: Final Thoughts Both Lisp and Prolog are based on formal mathematical models of computation: Prolog on logic and theorem proving, Lisp on the theory of recursive functions. This sets these languages apart from more traditional languages whose architecture is just an abstraction across the architecture of the underlying computing (von Neumann) hardware. By deriving their syntax and semantics from mathematical notations, Lisp and Prolog inherit both expressive power and clarity. Although Prolog, the newer of the two languages, has remained close to its theoretical roots, Lisp has been extended until it is no longer a purely functional programming language. The primary culprit for this diaspora was the Lisp community itself. The pure lisp core of the language is primarily an assembly language for building more complex data structures and search algorithms. Thus it was natural that each group of researchers or developers would “assemble” the Lisp environment that best suited their needs. After several decades of this the various dialects of Lisp were basically incompatible. The 1980s saw the desire to replace these multiple dialects with a core Common Lisp, which also included an object system, CLOS. Common Lisp is the Lisp language used in Part III. But the primary power of Lisp is the fact, as pointed out many times in Part III, that the data and commands of this language have a uniform structure. This supports the building of what we call meta-interpreters, or similarly, the use of meta-linguistic abstraction. This, simply put, is the ability of the program designer to build interpreters within Lisp (or Prolog) to interpret other suitably designed structures in the language. -

Drscheme: a Pedagogic Programming Environment for Scheme
DrScheme A Pedagogic Programming Environment for Scheme Rob ert Bruce Findler Cormac Flanagan Matthew Flatt Shriram Krishnamurthi and Matthias Felleisen Department of Computer Science Rice University Houston Texas Abstract Teaching intro ductory computing courses with Scheme el evates the intellectual level of the course and thus makes the sub ject more app ealing to students with scientic interests Unfortunatelythe p o or quality of the available programming environments negates many of the p edagogic advantages Toovercome this problem wehavedevel op ed DrScheme a comprehensive programming environmentforScheme It fully integrates a graphicsenriched editor a multilingua l parser that can pro cess a hierarchyofsyntactically restrictivevariants of Scheme a functional readevalprint lo op and an algebraical ly sensible printer The environment catches the typical syntactic mistakes of b eginners and pinp oints the exact source lo cation of runtime exceptions DrScheme also provides an algebraic stepp er a syntax checker and a static debugger The rst reduces Scheme programs including programs with assignment and control eects to values and eects The to ol is useful for explainin g the semantics of linguistic facilities and for studying the b ehavior of small programs The syntax c hecker annotates programs with fontandcolorchanges based on the syntactic structure of the pro gram It also draws arrows on demand that p oint from b ound to binding o ccurrences of identiers The static debugger roughly sp eaking pro vides a typ e inference system -

1. with Examples of Different Programming Languages Show How Programming Languages Are Organized Along the Given Rubrics: I
AGBOOLA ABIOLA CSC302 17/SCI01/007 COMPUTER SCIENCE ASSIGNMENT 1. With examples of different programming languages show how programming languages are organized along the given rubrics: i. Unstructured, structured, modular, object oriented, aspect oriented, activity oriented and event oriented programming requirement. ii. Based on domain requirements. iii. Based on requirements i and ii above. 2. Give brief preview of the evolution of programming languages in a chronological order. 3. Vividly distinguish between modular programming paradigm and object oriented programming paradigm. Answer 1i). UNSTRUCTURED LANGUAGE DEVELOPER DATE Assembly Language 1949 FORTRAN John Backus 1957 COBOL CODASYL, ANSI, ISO 1959 JOSS Cliff Shaw, RAND 1963 BASIC John G. Kemeny, Thomas E. Kurtz 1964 TELCOMP BBN 1965 MUMPS Neil Pappalardo 1966 FOCAL Richard Merrill, DEC 1968 STRUCTURED LANGUAGE DEVELOPER DATE ALGOL 58 Friedrich L. Bauer, and co. 1958 ALGOL 60 Backus, Bauer and co. 1960 ABC CWI 1980 Ada United States Department of Defence 1980 Accent R NIS 1980 Action! Optimized Systems Software 1983 Alef Phil Winterbottom 1992 DASL Sun Micro-systems Laboratories 1999-2003 MODULAR LANGUAGE DEVELOPER DATE ALGOL W Niklaus Wirth, Tony Hoare 1966 APL Larry Breed, Dick Lathwell and co. 1966 ALGOL 68 A. Van Wijngaarden and co. 1968 AMOS BASIC FranÇois Lionet anConstantin Stiropoulos 1990 Alice ML Saarland University 2000 Agda Ulf Norell;Catarina coquand(1.0) 2007 Arc Paul Graham, Robert Morris and co. 2008 Bosque Mark Marron 2019 OBJECT-ORIENTED LANGUAGE DEVELOPER DATE C* Thinking Machine 1987 Actor Charles Duff 1988 Aldor Thomas J. Watson Research Center 1990 Amiga E Wouter van Oortmerssen 1993 Action Script Macromedia 1998 BeanShell JCP 1999 AngelScript Andreas Jönsson 2003 Boo Rodrigo B. -

Programming Language Use in US Academia and Industry
Informatics in Education, 2015, Vol. 14, No. 2, 143–160 143 © 2015 Vilnius University DOI: 10.15388/infedu.2015.09 Programming Language Use in US Academia and Industry Latifa BEN ARFA RABAI1, Barry COHEN2, Ali MILI2 1 Institut Superieur de Gestion, Bardo, 2000, Tunisia 2 CCS, NJIT, Newark NJ 07102-1982 USA e-mail: [email protected], [email protected], [email protected] Received: July 2014 Abstract. In the same way that natural languages influence and shape the way we think, program- ming languages have a profound impact on the way a programmer analyzes a problem and formu- lates its solution in the form of a program. To the extent that a first programming course is likely to determine the student’s approach to program design, program analysis, and programming meth- odology, the choice of the programming language used in the first programming course is likely to be very important. In this paper, we report on a recent survey we conducted on programming language use in US academic institutions, and discuss the significance of our data by comparison with programming language use in industry. Keywords: programming language use, academic institution, academic trends, programming lan- guage evolution, programming language adoption. 1. Introduction: Programming Language Adoption The process by which organizations and individuals adopt technology trends is complex, as it involves many diverse factors; it is also paradoxical and counter-intuitive, hence difficult to model (Clements, 2006; Warren, 2006; John C, 2006; Leo and Rabkin, 2013; Geoffrey, 2002; Geoffrey, 2002a; Yi, Li and Mili, 2007; Stephen, 2006). This general observation applies to programming languages in particular, where many carefully de- signed languages that have superior technical attributes fail to be widely adopted, while languages that start with modest ambitions and limited scope go on to be widely used in industry and in academia. -
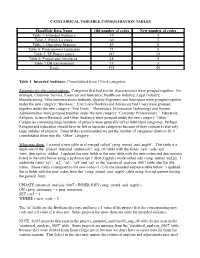
Categorical Variable Consolidation Tables
CATEGORICAL VARIABLE CONSOLIDATION TABLES FlossMole Data Name Old number of codes New number of codes Table 1: Intended Audience 19 5 Table 2: FOSS Licenses 60 7 Table 3: Operating Systems 59 8 Table 4: Programming languages 73 8 Table 5: SF Project topics 243 19 Table 6: Project user interfaces 48 9 Table 7 DB Environment 33 3 Totals 535 59 Table 1: Intended Audience: Consolidated from 19 to 4 categories Rationale for this consolidation: Categories that had similar characteristics were grouped together. For example, Customer Service, Financial and Insurance, Healthcare Industry, Legal Industry, Manufacturing, Telecommunications Industry, Quality Engineers and Aerospace were grouped together under the new category “Business.” End Users/Desktop and Advanced End Users were grouped together under the new category “End Users.” Developers, Information Technology and System Administrators were grouped together under the new category “Computer Professionals.” Education, Religion, Science/Research and Other Audience were grouped under the new category “Other.” Categories containing large numbers of projects were generally left as individual categories. Perhaps Religion and Education should have be left as separate categories because of they contain a relatively large number of projects. Since Mike recommended we get the number of categories down to 50, I consolidated them into the “Other” category. What was done: I created a new table in sf merged called ‘categ_intend_aud_aug06’. This table is a duplicate of the ‘project_intended_audience01_aug_06’ table with the fields ‘new_code’ and ‘new_description’ added. I updated the new fields in the new table with the new codes and descriptions listed in the table below using a python script I (Bob English) wrote called add_categ_intend_aud.py. -

From Krivine's Machine to the Caml Implementations
From Krivine's machine to the Caml implementations Xavier Leroy INRIA Rocquencourt 1 In this talk An illustration of the strengths and limitations of abstract machines for the purpose of e±cient execution of strict functional languages (Caml). 1. A retrospective on the ZAM, a call-by-value variant of Krivine's machine. 2. From abstract machines to e±cient P.L. implementations: the example of Caml Light and Objective Caml. 3. Beyond abstract machines: push-enter models vs. eval-apply models. 2 Why are abstract machines interesting? On the theory side (λ-calculus, semantics): Abstract machines expose concepts lacking or implicit in the λ-calculus: • Reduction strategy, evaluation order. • Data representations, esp. closures and environments. On the implementation side: Compilation to abstract machine code o®ers much better performance than interpreters. Abstract machine code as an intermediate language for machine-code generation. Abstract machine code as an architecture-independent low-level format for distributing compiled programs (JVM, .Net). 3 There are better ways In every area where abstract machines help, there are arguably better alternatives: • Exposing reduction order: CPS transformation, structured operational semantics, reduction contexts. • Closures and environments: explicit substitutions. • E±cient execution: optimizing compilation to real machine code. • Intermediate languages: RTL, SSA, CPS, A-normal forms, etc. • Code distribution: ANDF (?). Abstract machines do many things well but none very well. This we will illustrate in the case of e±cient execution of Caml. 4 A retrospective on the ZAM 5 The starting point The Caml language and implementation circa 1989: • Core ML (CBV λ-calculus) with primitives, data types and pattern-matching. -

The Definition of Standard ML, Revised
The Definition of Standard ML The Definition of Standard ML (Revised) Robin Milner, Mads Tofte, Robert Harper and David MacQueen The MIT Press Cambridge, Massachusetts London, England c 1997 Robin Milner All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher. Printed and bound in the United States of America. Library of Congress Cataloging-in-Publication Data The definition of standard ML: revised / Robin Milner ::: et al. p. cm. Includes bibliographical references and index. ISBN 0-262-63181-4 (alk. paper) 1. ML (Computer program language) I. Milner, R. (Robin), 1934- QA76.73.M6D44 1997 005:1303|dc21 97-59 CIP Contents 1 Introduction 1 2 Syntax of the Core 3 2.1 Reserved Words . 3 2.2 Special constants . 3 2.3 Comments . 4 2.4 Identifiers . 5 2.5 Lexical analysis . 6 2.6 Infixed operators . 6 2.7 Derived Forms . 7 2.8 Grammar . 7 2.9 Syntactic Restrictions . 9 3 Syntax of Modules 12 3.1 Reserved Words . 12 3.2 Identifiers . 12 3.3 Infixed operators . 12 3.4 Grammar for Modules . 13 3.5 Syntactic Restrictions . 13 4 Static Semantics for the Core 16 4.1 Simple Objects . 16 4.2 Compound Objects . 17 4.3 Projection, Injection and Modification . 17 4.4 Types and Type functions . 19 4.5 Type Schemes . 19 4.6 Scope of Explicit Type Variables . 20 4.7 Non-expansive Expressions . 21 4.8 Closure . -

Handout 0: Historical Development of “Programming” Concepts
06-02552 Princ. of Progr. Languages (and “Extended”) The University of Birmingham Spring Semester 2018-19 School of Computer Science c Uday Reddy2018-19 Handout 0: Historical development of “programming” concepts Digital computers were devised in the 1950’s and the activity of writing instructions for these computers came to be known as programming. However, “programming” in the broad sense of devising procedures, methods, recipes or rules for solving problems is much older, perhaps as old as humanity. As soon as human beings formed societies and started working together to carry out their daily activities, they needed to devise procedures for such activities and communicate them to each other, first in speech and then in writing. These ways of describing recipes are still in use pretty much the same way, and we use them in our daily lives, e.g., in following cooking recipes, using knitting patterns, or operating household gadgets. It is also in use in industrial and business contexts, e.g., for describing manufacturing processes on factory floor or business processes in organizations. “Programming” in mathematics is of special interest to us because it directly gave birth to programming in computer science. These programs are typically called algorithms, a term derived from the name of al-Khwarizmi, an Arab mathematician of 800 A.D., whose book Al-jabr wa’l muqabalah on algebraic manipulations was highly influential in the development of modern mathematics. The devising of mathematical algorithms began in pre-historic times as soon as numbers were invented to count and to measure. Methods were then needed for the arithmetic operations of addition, subtraction, multiplication, division and others. -

An Introduction to Landin's “A Generalization of Jumps and Labels”
Higher-Order and Symbolic Computation, 11, 117–123 (1998) c 1998 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. An Introduction to Landin’s “A Generalization of Jumps and Labels” HAYO THIELECKE [email protected] qmw, University of London Abstract. This note introduces Peter Landin’s 1965 technical report “A Generalization of Jumps and Labels”, which is reprinted in this volume. Its aim is to make that historic paper more accessible to the reader and to help reading it in context. To this end, we explain Landin’s control operator J in more contemporary terms, and we recall Burge’s solution to a technical problem in Landin’s original account. Keywords: J-operator, secd-machine, call/cc, goto, history of programming languages 1. Introduction In the mid-60’s, Peter Landin was investigating functional programming with “Applicative Expressions”, which he used to provide an account of Algol 60 [10]. To explicate goto, he introduced the operator J (for jump), in effect extending functional programming with control. This general control operator was powerful enough to have independent interest quite beyond the application to Algol: Landin documented the new paradigm in a series of technical reports [11, 12, 13]. The most significant of these reports is “A Generalization of Jumps and Labels” (reprinted in this volume on pages 9–27), as it presents and investigates the J-operator in its own right. The generalization is a radical one: it introduces first-class control into programming languages for the first time. Control is first-class in that the generalized labels given by the J-operator can be passed as arguments to and returned from procedures. -

Comparative Programming Languages CM20253
We have briefly covered many aspects of language design And there are many more factors we could talk about in making choices of language The End There are many languages out there, both general purpose and specialist And there are many more factors we could talk about in making choices of language The End There are many languages out there, both general purpose and specialist We have briefly covered many aspects of language design The End There are many languages out there, both general purpose and specialist We have briefly covered many aspects of language design And there are many more factors we could talk about in making choices of language Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important For example, can you easily join together code written in Java and C? The End Or languages And then the interopability of languages becomes important For example, can you easily join together code written in Java and C? The End Or languages Often a single project can use several languages, each suited to its part of the project For example, can you easily join together code written in Java and C? The End Or languages Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important The End Or languages Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important For example, can you easily