DOCSLIB.ORG

The Messenger

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Messenger The Messenger No. 124 – June 2006 Telescopes and Instrumentation CRIRES: Commissioning of the MACAO Adaptive Optics Module and General Status Report Hans Ulrich Käufl, Raul Esteves, veloped for the interferometry feed of the ment. This approach is also very much in Enrico Fedrigo, Domingo Gojak, VLT UTs, but were later also used for the line with the reintegration process at Jean-Louis Lizon, Enrico Marchetti, VLT instruments SINFONI and CRIRES the VLT. The integration, alignment and Sylvain Oberti, Jerome Paufique, (see Arsenault et al. 004, Bonnet et al. testing of the AO part require special Eszter Pozna, Sebastien Tordo (ESO) 004 or Paufique et al. 004; alternatively tools and a special test camera which in one can consult the ESO AO webpage turn require a sequential integration at the http://www.eso.org/projects/aot/ which telescope. The CRIRES warm-optics The installation and commissioning of contains detailed information). acceptance review took place at ESO on CRIRES, the Cryogenic Infrared Echelle 4 February 006, and thereafter packing Spectrograph, marks the completion In mid-005 the assembly and integration and shipment of the units could start, of the original plan for the first genera- activities of CRIRES had progressed such subject to few additional checks. Packing tion of VLT instrumentation. Here we that the in-depth verification of the per- of the ‘warm optics’ finally started on report on the commissioning of the cur- formance could be started. As the re- 8 February 006 and the crates left ESO vature sensing adaptive optics part quirements on stability and reproducibility Headquarters on 8 March 006. All (MACAO) of CRIRES in April 2006. This are relatively demanding this test phase boxes of this first batch arrived in good activity also brings the quasi-series pro- resulted in requests for a variety of modi- order on Paranal on 17 March and duction of the MACAO systems to an fications which did not allow keeping the were met by a joint team of the ESO In- end. All four UTs are now equipped with original schedule. strumentation and Telescope Systems one MACAO system each to feed inter- Divisions. Reintegration and installation of ferometry while UT1 and UT4 have one However, in February 006 CRIRES ulti- the components progressed rapidly with additional dedicated system each inte- mately passed the last fundamental mile- hardly any problem. grated into instruments. A summary of stone on its way to the VLT: the success- the overall status of CRIRES is given as ful completion of an ‘end-to-end’ test In the meantime, the CRIRES cold part well. of the system. Using a simulated cool star underwent further improvements and (black-body source and a gas cell with testing in Garching. By the time of writing CO mimicking a COmosphere1) and a tur- of this article the PAE for the complete CRIRES is a cryogenic, pre-dispersed, bulence generator to generate ‘seeing’, instrument had been granted and the infrared echelle spectrograph designed the overall stability of the system, that is spectrograph arrived in good order on to provide a resolving power l/Δl of the Adaptive Optics System and the Paranal on 5 May. The commissioning of 105 between 1 and 5 μm at the Nasmyth cryogenic spectrograph, was checked by the complete instrument will be reported focus A of the 8-m VLT Unit Telescope 1 recording spectra over many hours. in the next issue of The Messenger. (Antu). A curvature sensing adaptive op- The result of this test was that vibrations tics system feed is used to minimise slit and other instabilities are generally at losses and to provide diffraction-limited a level of the equivalent of 1/0th of a Testing the adaptive optics at the spatial resolution along the slit. The nomi- pixel (75 m/s Doppler shift equivalent) or telescope nal slit width of CRIRES is 0.2 arcsec. less and thus in line with the specifica- tions reflecting the astrophysical require- The commissioning of the warm-optics A mosaic of four Aladdin III InSb-arrays ments. part ran in parallel with the final pre- packaged on custom-fabricated ceramics paration for the second part of the PAE. boards has been developed. This pro- Thanks to the joint efforts of the team vides for an effective 4096 × 51 pixel How to move CRIRES from Garching and of Paranal staff, the integration and focal plane array, to maximise the free to the VLT realignment of the warm part in Paranal spectral range covered in each exposure. were successful: the MACAO system is Insertion of gas cells to measure high- Like any other VLT instrument, CRIRES now functional at full performance level. precision radial velocities is foreseen. had to pass the scrutiny of a review Spectro-polarimetry (circular and linear before shipment, termed PAE (Preliminary Figure 1a shows the adaptive-optics part polarisation) will be added in the course Acceptance Europe) in ‘ESO-speak’. of CRIRES after reintegration. For test of the project. To that end a cryogenic CRIRES consists of two relatively inde- purposes an infrared test camera with Wollaston prism in combination with re- pendent subunits: the adaptive optics a spatial sampling of 17 mas/pix (milli-arc- tarders for magnetic Doppler imaging part with the derotator, also carrying the seconds per pixel) was additionally in- is foreseen. CRIRES is part of the initial calibration facilities and the cryostat stalled to characterise the AO perform- first-generation instrumentation com- with the cryogenic optical bench. Hence ance (to be compared with the diffraction plement and is an in-house project done it was decided to split the PAE process limit: e.g. 1. l/D = 45 mas at 1.45 μm). by ESO (for an in-depth description of in two, and to have the ‘warm optics’ part In fact, once CRIRES is installed with its CRIRES see e.g. Moorwood 003 or reviewed ahead of the rest of the instru- infrared slit viewer, the sampling – Käufl et al. 004). The CRIRES MACAO system carries series number 6 of the 1 COmosphere is a term coined by Tom Ayres to highly successful ESO curvature sensor account for the very special chromospheres of cool AO systems which were originally de- stars dominated by the CO-molecule. The Messenger 124 – June 006 Figure 1a: A view of the CRIRES ‘warm optics’ near- Figure 1b: A team member, trying to sort out and re- ly completely installed on the Nasmyth A platform of connect the fibre bundle connecting the wave-front Antu (aka VLT UT1). The left electronics rack houses sensor lenslet array with the 60 avalanche photo di- most of the entire AO related electronics, that is the odes (APDs) contained in a special cabinet. The real-time computer, the local control unit (LCU), the APDs are solid-state photon-counting detectors. As adaptive mirror control and the power supplies for all curvature wavefront sensing systems basically need motors. Moreover the warm optics part comprises only one fast photometric channel per sub-pupil, the calibration unit with continuum sources, spectral APDs were given preference over CCD-detectors, lamps and the gas-cell slide, which allows to port due to their extremely low noise level (typically the ‘Iodine-cell-method’ for high-precision radial-ve- 0.4 counts per loop cycle). APDs, however, are very locity measurements into the infrared. The electron- sensitive and fragile devices, and the prevention of ics rack in the centre is an auxiliary rack for the in- accidental (and catastrophic) overexposures is a key frared test camera (which can be seen on the right issue. side in preparation: the shiny cryostat cylinder on a blue table). At this point a normal CCD camera is still used for alignment. For the reflection in the centre, see Figure 1b. 45 mas/pix – is no longer well suited to showing up as a ‘hot spot’. The system 4–13 August 006. In mid-June there will explore the AO-image quality (this cam- has proven its stability by observing in all be a first call for proposals for science era scale was chosen to be able to ex- typical seeing conditions from 0.5 up to verification programmes and at this point plore a larger field for offset-guiding). 1.5 arcsec. For bright stars with mR < 11, CRIRES will most likely be included in Figure 1b shows part of the integration. Strehl ratios in K-band above 55 % are the next call for proposals (P79). More obtained for median seeing conditions science verification is planned for P78 Figure (next page) shows details inside (0.8?, t0 between 3 and 4 ms at 0.5 μm), (1 October 006 to 31 March 007) and the MACAO box. The commissioning at the level of performance of the other potentially also an early start of opera- culminated within a few minutes of twi- MACAO units. tions of CRIRES for normal programmes light on 3 April to check the derotator selected by ESO’s OPC through the nor- algorithm. Official first light for the adap- mal selection process. tive optics part with the infrared test Outlook camera was on 6 April when the AO con- trol loop was closed at 3h4 UT on the The commissioning of the complete sys- References 5th-magnitude B-star Muscae. The tem is ongoing and everything is pre- h Arsenault R. et al. 004, The Messenger 117, 5 following commissioning tasks could be pared for first light on 4 June. A second Bonnet H. et al. 004, SPIE proc. 5490, 130 finished so smoothly that the team gave commissioning run and potentially some Käufl H.
Load more

Recommended publications
  • N6l0-Aistralian Observatory
    ^^—^^r N6L0-AISTRALIAN OBSERVATORY GAS DYNAMICS IN BARRED SPIRALS, II: NGC 7496 AND 289 V.D. Pence and C.P. BlackMn AAO PP 194 * Suonitted to: Mon.Not.R.astr.Soc. Distribution date: February, 1984 P.O. BOX 296. EPPING. N.S.W.. 2121 PHONE 868-1666. TELEX ASTRO 26230 „. *u~ - .*.SÄ._TNW. - Afto-<?(*-- ^M GAS DYNAMICS IN BARRED SPIRALS, II: NGC 7496 AND 289 W.D.Pence. Anglo-Australian Observatory. P.O. Box 296. Epplng. NSW. Australia. C.P.Blactanan. Department of Astronomy. Edinburgh University. Received t SUMMAKT - The gas velocity fields in the barred spiral galaxies NGC 7496 and 289 have been measured by means of long-slit spectra obtained with the Anglo-Australian Telescope. Pronounced deviations fro« circular motion of the type predicted by recent theoretical mooels are seen in NGC 74961 the isovelocity contours are distorted into a characteristic S-shaped pattern and there is a large velocity gradient across the bar. The velocity field is virtually identical to that of a previously observed barred spiral, NGC 5383 for which a number of models have been published. The nuclear [OUI] emission lines are very asymmetric with a wing extending to about 1000 km s-1 to the blue of the systemic velocity; this wing is only faintly seen in the Balmer lines. NGC 289 has a much smaller bar *nd consequently the noncircular motions are less pronounced. The most obvious effect is that the Xinematic major and minor axes are not perpendicular which is a signature of oval distortions. Both galaxies have a mass (within the 10 outermost velocity measurement) of 9 x iO M0 and M/Lß » 6.
    [Show full text]
  • The Puzzling Nature of Dwarf-Sized Gas Poor Disk Galaxies
    Dissertation submitted to the Department of Physics Combined Faculties of the Astronomy Division Natural Sciences and Mathematics University of Oulu Ruperto-Carola-University Oulu, Finland Heidelberg, Germany for the degree of Doctor of Natural Sciences Put forward by Joachim Janz born in: Heidelberg, Germany Public defense: January 25, 2013 in Oulu, Finland THE PUZZLING NATURE OF DWARF-SIZED GAS POOR DISK GALAXIES Preliminary examiners: Pekka Heinämäki Helmut Jerjen Opponent: Laura Ferrarese Joachim Janz: The puzzling nature of dwarf-sized gas poor disk galaxies, c 2012 advisors: Dr. Eija Laurikainen Dr. Thorsten Lisker Prof. Heikki Salo Oulu, 2012 ABSTRACT Early-type dwarf galaxies were originally described as elliptical feature-less galax- ies. However, later disk signatures were revealed in some of them. In fact, it is still disputed whether they follow photometric scaling relations similar to giant elliptical galaxies or whether they are rather formed in transformations of late- type galaxies induced by the galaxy cluster environment. The early-type dwarf galaxies are the most abundant galaxy type in clusters, and their low-mass make them susceptible to processes that let galaxies evolve. Therefore, they are well- suited as probes of galaxy evolution. In this thesis we explore possible relationships and evolutionary links of early- type dwarfs to other galaxy types. We observed a sample of 121 galaxies and obtained deep near-infrared images. For analyzing the morphology of these galaxies, we apply two-dimensional multicomponent fitting to the data. This is done for the first time for a large sample of early-type dwarfs. A large fraction of the galaxies is shown to have complex multicomponent structures.
    [Show full text]
  • Arxiv:1306.3244V2 [Astro-Ph.CO] 4 Feb 2014
    The Scientific Reach of Multi-Ton Scale Dark Matter Direct Detection Experiments Jayden L. Newsteada, Thomas D. Jacquesa, Lawrence M. Kraussa;b, James B. Dentc, and Francesc Ferrerd a Department of Physics and School of Earth and Space Exploration, Arizona State University, Tempe, AZ 85287, USA, b Research School of Astronomy and Astrophysics, Mt. Stromlo Observatory, Australian National University, Canberra 2614, Australia, c Department of Physics, University of Louisiana at Lafayette, Lafayette, LA 70504, USA, and d Physics Department and McDonnell Center for the Space Sciences, Washington University, St Louis, MO 63130, USA (Dated: November 6, 2018) Abstract The next generation of large scale WIMP direct detection experiments have the potential to go beyond the discovery phase and reveal detailed information about both the particle physics and astrophysics of dark matter. We report here on early results arising from the development of a detailed numerical code modeling the proposed DARWIN detector, involving both liquid argon and xenon targets. We incorporate realistic detector physics, particle physics and astrophysical uncertainties and demonstrate to what extent two targets with similar sensitivities can remove various degeneracies and allow a determination of dark matter cross sections and masses while also probing rough aspects of the dark matter phase space distribution. We find that, even assuming arXiv:1306.3244v2 [astro-ph.CO] 4 Feb 2014 dominance of spin-independent scattering, multi-ton scale experiments still have degeneracies that depend sensitively on the dark matter mass, and on the possibility of isospin violation and inelas- ticity in interactions. We find that these experiments are best able to discriminate dark matter properties for dark matter masses less than around 200 GeV.
    [Show full text]
  • The Boundary of Galaxy Clusters and Its Implications on SFR Quenching
    The splashback boundary of galaxy clusters in mass and light and its implications for galaxy evolution T.-H. Shin, Ph.D. candidate at UPenn Collaborators: S. Adhikari, E. J. Baxter, C. Chang, B. Jain, N. Battaglia et al. (DES collaboration) (SPT collaboration) (ACT collaboration) https://arxiv.org/abs/1811.06081 (accepted to MNRAS); 2019 paper in preparation Based on ~400 public cluster sample from ACT+SPT Ongoing analysis of 1000+ SZ-selected clusters from DES+ACT+SPT Background Mass and boundary of dark matter halos However, MΔ and RΔ are subject to pseudo-evolution due to the decrease in the ρ ρ reference density ( c or m) Haloes continuously accrete matter; there is no radius within which the matter is fully virialized ⇒ where is the physical boundary of the halos? Credit: Andrey Kravtsov Cosmology with galaxy clusters Galaxy clusters live in the high-mass tail of the halo mass function ⇒ very sensitive to the growth of the structure Ω σ ( m and 8) Thus, it is important to accurately define/measure Tinker et al. (2008) the mass of the cluster Preliminary work by Diemer et al. illuminates that the mass function becomes more universal against redshift when we use so-called “splashback radius” as the physical boundary of the dark matter halos Background ● Galaxies fall into the cluster potential, escaping from the Hubble flow ● They form a sharp “physical” boundary around their first apocenters after the infall, which we call “splashback radius” Background ● A simple spherical collapse model can predict the existence of the splashback feature (Gunn & Gott 1972, Fillmore & Goldreich 1984, Bertschinger 1985, Adhikari et al.
    [Show full text]
  • Dark Matter 18Th May 2021.Pdf
    Searches for Dark Matter Seminar presentation 18th May 2021 Iida Kostamo 1/20 Contents • Background and history - How did we end up with the dark matter hypothesis? • Hot and cold dark matter - Candidates for cold dark matter • The halo density profile • Simulations (Millennium and Bolshoi) • Summary Seminar presentation 18th May 2021 Iida Kostamo 2/20 Background • The total mass-energy density of the universe (approximately): 1. 5% ordinary baryonic matter 2. 25% dark matter 3. 70% dark energy • Originally dark matter was referred to as "the missing mass" - 1930's: Fritz Zwicky did research on galaxy clusters • ...The problem is the missing light, not the missing mass, hence "dark matter" Seminar presentation 18th May 2021 Iida Kostamo 3/20 The rotation curves of galaxies • The rotation curve describes how the rotation velocity of an object depends on the distance from the center of the galaxy • Assumption: Kepler's III law, i.e. the rotation velocities decrease with increasing distance • In the 1970's Vera Rubin and her colleagues did research on the rotation curves of various spiral galaxies Seminar presentation 18th May 2021 Iida Kostamo 4/20 The rotation curves of galaxies • H = Hubble constant • The rotation curves become flat when the radius is large enough • The same result for all galaxies: the rotation curves are not descending → There must be non-luminous mass in galaxies Seminar presentation 18th May 2021 Iida Kostamo 5/20 MACHOs (Massive Astrophysical Compact Halo Object) • Objects that emit extremely little or no light →
    [Show full text]
  • And Ecclesiastical Cosmology
    GSJ: VOLUME 6, ISSUE 3, MARCH 2018 101 GSJ: Volume 6, Issue 3, March 2018, Online: ISSN 2320-9186 www.globalscientificjournal.com DEMOLITION HUBBLE'S LAW, BIG BANG THE BASIS OF "MODERN" AND ECCLESIASTICAL COSMOLOGY Author: Weitter Duckss (Slavko Sedic) Zadar Croatia Pусскй Croatian „If two objects are represented by ball bearings and space-time by the stretching of a rubber sheet, the Doppler effect is caused by the rolling of ball bearings over the rubber sheet in order to achieve a particular motion. A cosmological red shift occurs when ball bearings get stuck on the sheet, which is stretched.“ Wikipedia OK, let's check that on our local group of galaxies (the table from my article „Where did the blue spectral shift inside the universe come from?“) galaxies, local groups Redshift km/s Blueshift km/s Sextans B (4.44 ± 0.23 Mly) 300 ± 0 Sextans A 324 ± 2 NGC 3109 403 ± 1 Tucana Dwarf 130 ± ? Leo I 285 ± 2 NGC 6822 -57 ± 2 Andromeda Galaxy -301 ± 1 Leo II (about 690,000 ly) 79 ± 1 Phoenix Dwarf 60 ± 30 SagDIG -79 ± 1 Aquarius Dwarf -141 ± 2 Wolf–Lundmark–Melotte -122 ± 2 Pisces Dwarf -287 ± 0 Antlia Dwarf 362 ± 0 Leo A 0.000067 (z) Pegasus Dwarf Spheroidal -354 ± 3 IC 10 -348 ± 1 NGC 185 -202 ± 3 Canes Venatici I ~ 31 GSJ© 2018 www.globalscientificjournal.com GSJ: VOLUME 6, ISSUE 3, MARCH 2018 102 Andromeda III -351 ± 9 Andromeda II -188 ± 3 Triangulum Galaxy -179 ± 3 Messier 110 -241 ± 3 NGC 147 (2.53 ± 0.11 Mly) -193 ± 3 Small Magellanic Cloud 0.000527 Large Magellanic Cloud - - M32 -200 ± 6 NGC 205 -241 ± 3 IC 1613 -234 ± 1 Carina Dwarf 230 ± 60 Sextans Dwarf 224 ± 2 Ursa Minor Dwarf (200 ± 30 kly) -247 ± 1 Draco Dwarf -292 ± 21 Cassiopeia Dwarf -307 ± 2 Ursa Major II Dwarf - 116 Leo IV 130 Leo V ( 585 kly) 173 Leo T -60 Bootes II -120 Pegasus Dwarf -183 ± 0 Sculptor Dwarf 110 ± 1 Etc.
    [Show full text]
  • Analytical Properties of Einasto Dark Matter Haloes
    A&A 540, A70 (2012) Astronomy DOI: 10.1051/0004-6361/201118543 & c ESO 2012 Astrophysics Analytical properties of Einasto dark matter haloes E. Retana-Montenegro1 , E. Van Hese2, G. Gentile2,M.Baes2, and F. Frutos-Alfaro1 1 Escuela de Física, Universidad de Costa Rica, 11501 San Pedro, Costa Rica e-mail: [email protected] 2 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281-S9, 9000 Gent, Belgium e-mail: [email protected] Received 29 November 2011 / Accepted 19 January 2012 ABSTRACT Recent high-resolution N-body CDM simulations indicate that nonsingular three-parameter models such as the Einasto profile perform better than the singular two-parameter models, e.g. the Navarro, Frenk and White, in fitting a wide range of dark matter haloes. While many of the basic properties of the Einasto profile have been discussed in previous studies, a number of analytical properties are still not investigated. In particular, a general analytical formula for the surface density, an important quantity that defines the lensing properties of a dark matter halo, is still lacking to date. To this aim, we used a Mellin integral transform formalism to derive a closed expression for the Einasto surface density and related properties in terms of the Fox H and Meijer G functions, which can be written as series expansions. This enables arbitrary-precision calculations of the surface density and the lensing properties of realistic dark matter halo models. Furthermore, we compared the Sérsic and Einasto surface mass densities and found differences between them, which implies that the lensing properties for both profiles differ.
    [Show full text]
  • Modified Newtonian Dynamics, an Introductory Review
    Modified Newtonian Dynamics, an Introductory Review Riccardo Scarpa European Southern Observatory, Chile E-mail [email protected] Abstract. By the time, in 1937, the Swiss astronomer Zwicky measured the velocity dispersion of the Coma cluster of galaxies, astronomers somehow got acquainted with the idea that the universe is filled by some kind of dark matter. After almost a century of investigations, we have learned two things about dark matter, (i) it has to be non-baryonic -- that is, made of something new that interact with normal matter only by gravitation-- and, (ii) that its effects are observed in -8 -2 stellar systems when and only when their internal acceleration of gravity falls below a fix value a0=1.2×10 cm s . Being completely decoupled dark and normal matter can mix in any ratio to form the objects we see in the universe, and indeed observations show the relative content of dark matter to vary dramatically from object to object. This is in open contrast with point (ii). In fact, there is no reason why normal and dark matter should conspire to mix in just the right way for the mass discrepancy to appear always below a fixed acceleration. This systematic, more than anything else, tells us we might be facing a failure of the law of gravity in the weak field limit rather then the effects of dark matter. Thus, in an attempt to avoid the need for dark matter many modifications of the law of gravity have been proposed in the past decades. The most successful – and the only one that survived observational tests -- is the Modified Newtonian Dynamics.
    [Show full text]
  • Disk Galaxy Rotation Curves and Dark Matter Distribution
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server Disk galaxy rotation curves and dark matter distribution by Dilip G. Banhatti School of Physics, Madurai-Kamaraj University, Madurai 625021, India [Based on a pedagogic / didactic seminar given by DGB at the Graduate College “High Energy & Particle Astrophysics” at Karlsruhe in Germany on Friday the 20 th January 2006] Abstract . After explaining the motivation for this article, we briefly recapitulate the methods used to determine the rotation curves of our Galaxy and other spiral galaxies in their outer parts, and the results of applying these methods. We then present the essential Newtonian theory of (disk) galaxy rotation curves. The next two sections present two numerical simulation schemes and brief results. Finally, attempts to apply Einsteinian general relativity to the dynamics are described. The article ends with a summary and prospects for further work in this area. Recent observations and models of the very inner central parts of galaxian rotation curves are omitted, as also attempts to apply modified Newtonian dynamics to the outer parts. Motivation . Extensive radio observations determined the detailed rotation curve of our Milky Way Galaxy as well as other (spiral) disk galaxies to be flat much beyond their extent as seen in the optical band. Assuming a balance between the gravitational and centrifugal forces within Newtonian mechanics, the orbital speed V is expected to fall with the galactocentric distance r as V 2 = GM/r beyond the physical extent of the galaxy of mass M, G being the gravitational constant.
    [Show full text]
  • Cosmology Meets Condensed Matter
    Cosmology Meets Condensed Matter Mark N. Brook Thesis submitted to the University of Nottingham for the degree of Doctor of Philosophy. July 2010 The Feynman Problem-Solving Algorithm: 1. Write down the problem 2. Think very hard 3. Write down the answer – R. P. Feynman att. to M. Gell-Mann Supervisor: Prof. Peter Coles Examiners: Prof. Ed Copeland Prof. Ray Rivers Abstract This thesis is concerned with the interface of cosmology and condensed matter. Although at either end of the scale spectrum, the two disciplines have more in common than one might think. Condensed matter theorists and high-energy field theorists study, usually independently, phenomena embedded in the structure of a quantum field theory. It would appear at first glance that these phenomena are disjoint, and this has often led to the two fields developing their own procedures and strategies, and adopting their own nomenclature. We will look at some concepts that have helped bridge the gap between the two sub- jects, enabling progress in both, before incorporating condensed matter techniques to our own cosmological model. By considering ideas from cosmological high-energy field theory, we then critically examine other models of astrophysical condensed mat- ter phenomena. In Chapter 1, we introduce the current cosmological paradigm, and present a somewhat historical overview of the interplay between cosmology and condensed matter. Many concepts are introduced here that later chapters will follow up on, and we give some examples in which condensed matter physics has had a very real effect on informing cosmology. We also reflect on the most recent incarnations of the condensed matter / cosmology interplay, and the future of these developments.
    [Show full text]
  • 00E the Construction of the Universe Symphony
    The basic construction of the Universe Symphony. There are 30 asterisms (Suites) in the Universe Symphony. I divided the asterisms into 15 groups. The asterisms in the same group, lay close to each other. Asterisms!! in Constellation!Stars!Objects nearby 01 The W!!!Cassiopeia!!Segin !!!!!!!Ruchbah !!!!!!!Marj !!!!!!!Schedar !!!!!!!Caph !!!!!!!!!Sailboat Cluster !!!!!!!!!Gamma Cassiopeia Nebula !!!!!!!!!NGC 129 !!!!!!!!!M 103 !!!!!!!!!NGC 637 !!!!!!!!!NGC 654 !!!!!!!!!NGC 659 !!!!!!!!!PacMan Nebula !!!!!!!!!Owl Cluster !!!!!!!!!NGC 663 Asterisms!! in Constellation!Stars!!Objects nearby 02 Northern Fly!!Aries!!!41 Arietis !!!!!!!39 Arietis!!! !!!!!!!35 Arietis !!!!!!!!!!NGC 1056 02 Whale’s Head!!Cetus!! ! Menkar !!!!!!!Lambda Ceti! !!!!!!!Mu Ceti !!!!!!!Xi2 Ceti !!!!!!!Kaffalijidhma !!!!!!!!!!IC 302 !!!!!!!!!!NGC 990 !!!!!!!!!!NGC 1024 !!!!!!!!!!NGC 1026 !!!!!!!!!!NGC 1070 !!!!!!!!!!NGC 1085 !!!!!!!!!!NGC 1107 !!!!!!!!!!NGC 1137 !!!!!!!!!!NGC 1143 !!!!!!!!!!NGC 1144 !!!!!!!!!!NGC 1153 Asterisms!! in Constellation Stars!!Objects nearby 03 Hyades!!!Taurus! Aldebaran !!!!!! Theta 2 Tauri !!!!!! Gamma Tauri !!!!!! Delta 1 Tauri !!!!!! Epsilon Tauri !!!!!!!!!Struve’s Lost Nebula !!!!!!!!!Hind’s Variable Nebula !!!!!!!!!IC 374 03 Kids!!!Auriga! Almaaz !!!!!! Hoedus II !!!!!! Hoedus I !!!!!!!!!The Kite Cluster !!!!!!!!!IC 397 03 Pleiades!! ! Taurus! Pleione (Seven Sisters)!! ! ! Atlas !!!!!! Alcyone !!!!!! Merope !!!!!! Electra !!!!!! Celaeno !!!!!! Taygeta !!!!!! Asterope !!!!!! Maia !!!!!!!!!Maia Nebula !!!!!!!!!Merope Nebula !!!!!!!!!Merope
    [Show full text]
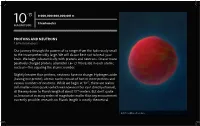
  • Protons and Neutrons 1.6 Femtometers Our Journey Through
    -15 0.000,000,000,000,001 m 10 1 Femtometer MAGNITUDE PROTONS AND NEUTRONS 1.6 Femtometers Our journey through the powers of 10 ranges from the ludicrously small to the incomprehensibly large. We will do our best not to break your brain. We begin subatomically, with protons and neutrons. One or more positively charged protons (diameter 1.6−1.7 fm) reside in each atomic nucleus—this equaling the atomic number. Slightly heavier than protons, neutrons have no charge. Hydrogen aside (having one proton), atomic nuclei consist of two or more protons and various numbers of neutrons. While we begin at 10-15, there are realms still smaller—from quarks (which we know exist but can’t directly observe), all the way down to Planck length at about 10-35 meters. But don’t quote us, because at so many orders of magnitude smaller than any measurement currently possible, research on Planck length is mostly theoretical. Artist’s rendition of a proton. -14 0.000,000,000,000,01 m 10 10 Femtometers MAGNITUDE AOT MIC NUCLEUS OF A URANIUM ATOM 15 Femtometers As we take the first tentative steps on our journey of scale, we arrive at some of the very building blocks (even though they look round) of existence. The atomic nucleus is the dense region consisting of positively charged protons and electrically neutral neutrons at the center of the basic unit of matter, the atom. Almost all of an atom’s mass is located in its nucleus, the rest provided by its orbiting cloud of negatively charged electrons.
    [Show full text]