Grade 6 Math Circles the Mathematics of Voting
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2019-20 Upper Deck ICE Hockey Checklist
19/20 UD ICE Hockey Checklist Blue = Auto/Relics; White = Base/Inserts/Non-Hits Player Set Card # Team Print Run Cale Makar Auto - Exquisite Rookie SIgnatures Auto + Parallels R23 Avalanche 125 Cale Makar Auto - Ice Premieres IPA-CM Avalanche 99 Cale Makar Auto - Rookie Ice Buckets + Red Parallel IBR-CM Avalanche 109 Cale Makar Auto - Sub Zero Rookie Variants Green SZ-44V Avalanche 25 Cale Makar Auto - Sub Zero Stars - Rookie - Blue Parallel SZ-44 Avalanche Cale Makar Auto - Superb Script SS-CM Avalanche 25 Cale Makar Auto - Superb Script Portraits SS-CM Avalanche 10 Cale Makar Auto - Under Glass Rookie Signatures UG-MA Avalanche Cale Makar Auto - Under Glass Rookie Signatures Red UG-MA Avalanche 5 Cale Makar Auto Relic - Exquisite 03/04 RPA Tribute + Black Parallel 03T-CM Avalanche 26 Cale Makar Auto Relic - Exquisite 09/10 RPA Tribute + Parallels 09T-CM Avalanche 125 Cale Makar Auto Relic - Ice Premieres Auto Patch IP-CM Avalanche 10 Cale Makar Auto Relic - Signature Swatches + Patch Parallel SW-MA Avalanche 165 Cale Makar Relic - Ice Premieres Jersey IPJ-CM Avalanche Cale Makar Relic - Rookie Relic Jumbos + Patch Parallel RRJ-CM Avalanche 214 Conor Timmins Relic - Ice Premieres Jersey IPJ-CT Avalanche Joe Sakic Auto - 18/19 Ice - Glacial Graphs GG-JS Avalanche Joe Sakic Auto - 18/19 Ice - Glacial Graphs Black GG-JS Avalanche 5 Mikko Rantanen Auto - 18/19 Ice - Glacial Graphs GG-MR Avalanche Mikko Rantanen Relic - Base Jersey 19 Avalanche Mikko Rantanen Relic - Base Patch Gold 19 Avalanche 15 Mikko Rantanen Auto - 18/19 Ice - Glacial -
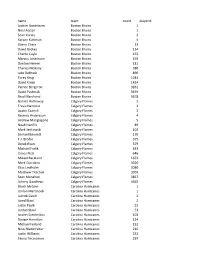
2019 Playoff Draft Player Frequency Report
name team count playerid Joakim Nordstrom Boston Bruins 1 Noel Acciari Boston Bruins 1 Sean Kuraly Boston Bruins 3 Karson Kuhlman Boston Bruins 4 Zdeno Chara Boston Bruins 13 David Backes Boston Bruins 134 Charlie Coyle Boston Bruins 153 Marcus Johansson Boston Bruins 159 Danton Heinen Boston Bruins 181 Charles McAvoy Boston Bruins 380 Jake DeBrusk Boston Bruins 890 Torey Krug Boston Bruins 1044 David Krejci Boston Bruins 1434 Patrice Bergeron Boston Bruins 3261 David Pastrnak Boston Bruins 3459 Brad Marchand Boston Bruins 3678 Garnet Hathaway Calgary Flames 2 Travis Hamonic Calgary Flames 2 Austin Czarnik Calgary Flames 3 Rasmus Andersson Calgary Flames 4 Andrew Mangiapane Calgary Flames 5 Noah Hanifin Calgary Flames 89 Mark Jankowski Calgary Flames 102 Samuel Bennett Calgary Flames 170 T.J. Brodie Calgary Flames 375 Derek Ryan Calgary Flames 379 Michael Frolik Calgary Flames 633 James Neal Calgary Flames 646 Mikael Backlund Calgary Flames 1653 Mark Giordano Calgary Flames 3020 Elias Lindholm Calgary Flames 3080 Matthew Tkachuk Calgary Flames 3303 Sean Monahan Calgary Flames 3857 Johnny Gaudreau Calgary Flames 4363 Brock McGinn Carolina Hurricanes 1 Jordan Martinook Carolina Hurricanes 1 Jaccob Slavin Carolina Hurricanes 2 Jared Staal Carolina Hurricanes 2 Justin Faulk Carolina Hurricanes 22 Jordan Staal Carolina Hurricanes 53 Andrei Svechnikov Carolina Hurricanes 103 Dougie Hamilton Carolina Hurricanes 124 Michael Ferland Carolina Hurricanes 152 Nino Niederreiter Carolina Hurricanes 216 Justin Williams Carolina Hurricanes 232 Teuvo Teravainen Carolina Hurricanes 297 Sebastian Aho Carolina Hurricanes 419 Nikita Zadorov Colorado Avalanche 1 Samuel Girard Colorado Avalanche 1 Matthew Nieto Colorado Avalanche 1 Cale Makar Colorado Avalanche 2 Erik Johnson Colorado Avalanche 2 Tyson Jost Colorado Avalanche 3 Josh Anderson Colorado Avalanche 14 Colin Wilson Colorado Avalanche 14 Matt Calvert Colorado Avalanche 14 Derick Brassard Colorado Avalanche 28 J.T. -

Dallas Stars Game Notes
Dallas Stars Game Notes Fri, Jan 4, 2019 NHL Game #632 Dallas Stars 21 - 16 - 4 (46 pts) Washington Capitals 24 - 12 - 3 (51 pts) Team Game: 42 13 - 5 - 2 (Home) Team Game: 40 12 - 6 - 2 (Home) Home Game: 21 8 - 11 - 2 (Road) Road Game: 20 12 - 6 - 1 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 30 Ben Bishop 26 14 9 2 2.35 .923 1 Pheonix Copley 13 9 2 1 2.61 .914 35 Anton Khudobin 18 7 7 2 2.63 .920 70 Braden Holtby 28 15 10 2 2.92 .910 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 3 D John Klingberg 23 5 12 17 2 4 2 D Matt Niskanen 37 5 10 15 -1 24 4 D Miro Heiskanen 41 9 10 19 -5 10 6 D Michal Kempny 36 4 10 14 22 34 5 D Connor Carrick 10 1 3 4 -6 4 8 L Alex Ovechkin 39 30 16 46 11 18 6 D Julius Honka 24 0 4 4 0 10 9 D Dmitry Orlov 39 2 10 12 -5 23 12 C Radek Faksa 41 7 8 15 -8 27 10 R Brett Connolly 39 9 14 23 6 10 13 C Mattias Janmark 41 3 11 14 -4 14 13 L Jakub Vrana 39 12 9 21 13 14 14 L Jamie Benn 41 17 15 32 6 32 18 C Chandler Stephenson 37 5 4 9 -6 0 15 L Blake Comeau 40 4 3 7 -10 16 19 C Nicklas Backstrom 39 10 34 44 13 12 17 C Devin Shore 37 5 12 17 1 7 20 C Lars Eller 39 5 12 17 -7 25 18 C Tyler Pitlick 36 6 4 10 1 6 22 D Madison Bowey 29 1 5 6 4 38 23 D Esa Lindell 41 6 11 17 1 22 23 R Dmitrij Jaskin 27 1 6 7 1 0 24 L Roope Hintz 17 2 2 4 -3 10 25 R Devante Smith-Pelly 37 4 4 8 -1 4 25 R Brett Ritchie 22 2 2 4 0 25 26 C Nic Dowd 33 4 9 13 7 12 27 R Erik Condra - - - - - - 34 D Jonas Siegenthaler 13 0 3 3 6 4 42 D Taylor Fedun 18 2 4 6 5 4 43 R Tom Wilson 20 11 8 19 11 37 43 R Valeri Nichushkin 32 0 7 7 -4 0 44 D Brooks Orpik 12 1 1 2 0 6 45 D Roman Polak 38 1 2 3 3 43 65 L Andre Burakovsky 35 5 3 8 -4 8 47 R Alexander Radulov 31 13 21 34 8 32 72 C Travis Boyd 20 3 7 10 8 4 90 C Jason Spezza 39 6 15 21 -4 15 74 D John Carlson 38 6 33 39 22 10 91 C Tyler Seguin 41 13 23 36 13 10 77 R T.J. -

Tampa Bay Lightning Game Notes
Tampa Bay Lightning Game Notes Thu, Feb 14, 2019 NHL Game #880 Tampa Bay Lightning 42 - 11 - 4 (88 pts) Dallas Stars 29 - 22 - 5 (63 pts) Team Game: 58 22 - 5 - 2 (Home) Team Game: 57 18 - 8 - 2 (Home) Home Game: 30 20 - 6 - 2 (Road) Road Game: 29 11 - 14 - 3 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 70 Louis Domingue 22 18 4 0 2.90 .907 35 Anton Khudobin 25 10 10 3 2.34 .927 88 Andrei Vasilevskiy 34 23 7 4 2.45 .925 41 Landon Bow 1 0 0 0 0.00 1.00 0 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 5 D Dan Girardi 52 3 9 12 5 10 2 D Jamie Oleksiak 43 4 7 11 6 41 6 D Anton Stralman 37 2 13 15 10 8 3 D John Klingberg 38 7 20 27 9 10 7 R Mathieu Joseph 48 13 7 20 7 12 4 D Miro Heiskanen 56 10 15 25 -8 10 9 C Tyler Johnson 55 19 16 35 9 20 5 D Connor Carrick 13 1 3 4 -6 13 10 C J.T. Miller 51 9 23 32 1 12 6 D Julius Honka 29 0 4 4 -2 10 13 C Cedric Paquette 56 9 4 13 5 58 12 C Radek Faksa 56 9 11 20 -10 35 17 L Alex Killorn 57 11 17 28 15 35 13 C Mattias Janmark 56 5 14 19 -5 18 18 L Ondrej Palat 39 7 14 21 1 12 14 L Jamie Benn 55 19 20 39 10 44 21 C Brayden Point 56 33 39 72 15 20 15 L Blake Comeau 55 6 4 10 -11 22 24 R Ryan Callahan 43 6 9 15 7 14 16 C Jason Dickinson 41 5 8 13 3 16 27 D Ryan McDonagh 57 5 24 29 23 26 17 C Andrew Cogliano 56 4 10 14 2 20 37 C Yanni Gourde 57 15 19 34 4 42 23 D Esa Lindell 56 8 16 24 6 27 55 D Braydon Coburn 52 3 11 14 2 24 24 L Roope Hintz 32 3 5 8 -3 14 62 L Danick Martel 7 0 2 2 4 6 25 R Brett Ritchie 33 4 2 6 0 44 71 C Anthony Cirelli 57 11 11 22 12 15 34 R Denis Gurianov 18 -

2021 Nhl Awards Presented by Bridgestone Information Guide
2021 NHL AWARDS PRESENTED BY BRIDGESTONE INFORMATION GUIDE TABLE OF CONTENTS 2021 NHL Award Winners and Finalists ................................................................................................................................. 3 Regular-Season Awards Art Ross Trophy ......................................................................................................................................................... 4 Bill Masterton Memorial Trophy ................................................................................................................................. 6 Calder Memorial Trophy ............................................................................................................................................. 8 Frank J. Selke Trophy .............................................................................................................................................. 14 Hart Memorial Trophy .............................................................................................................................................. 18 Jack Adams Award .................................................................................................................................................. 24 James Norris Memorial Trophy ................................................................................................................................ 28 Jim Gregory General Manager of the Year Award ................................................................................................. -
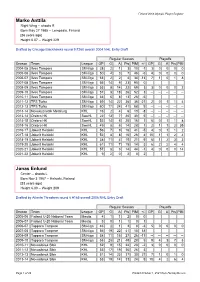
Finland Olympic Player Register At
Finland 2018 Olympic Player Register Marko Anttila Right Wing -- shoots R Born May 27 1985 -- Lempaala, Finland [36 years ago] Height 6.07 -- Weight 229 Drafted by Chicago Blackhawks round 9 #260 overall 2004 NHL Entry Draft Regular Season Playoffs Season Team League GP G A Pts PIM +/- GP G A Pts PIM 2004-05 Ilves Tampere SM-liiga 28 2 1 3 10 -1 3 0 0 0 0 2005-06 Ilves Tampere SM-liiga 50 4 3 7 46 -6 4 0 0 0 0 2006-07 Ilves Tampere SM-liiga 53 2 2 4 34 -13 7 1 0 1 8 2007-08 Ilves Tampere SM-liiga 56 14 9 23 90 0 2008-09 Ilves Tampere SM-liiga 53 8 14 22 69 3 3 0 0 0 2 2009-10 Ilves Tampere SM-liiga 57 8 18 26 52 3 -- -- -- -- -- 2010-11 Ilves Tampere SM-liiga 33 5 8 13 26 -5 2011-12 TPS Turku SM-liiga 59 14 22 36 36 -21 2 0 1 1 4 2012-13 TPS Turku SM-liiga 60 17 24 41 68 9 -- -- -- -- -- 2013-14 Novokuznetsk Metallurg KHL 16 2 4 6 10 -8 -- -- -- -- -- 2013-14 Orebro HK SweHL 22 13 7 20 30 5 -- -- -- -- -- 2014-15 Orebro HK SweHL 52 14 6 20 16 1 6 0 1 1 8 2015-16 Orebro HK SweHL 49 8 6 14 28 1 2 1 1 2 35 2016-17 Jokerit Helsinki KHL 56 7 9 16 41 -5 4 0 1 1 2 2017-18 Jokerit Helsinki KHL 52 8 8 16 26 4 10 1 1 2 4 2018-19 Jokerit Helsinki KHL 38 11 4 15 21 9 6 1 2 3 3 2019-20 Jokerit Helsinki KHL 61 11 7 18 14 3 6 2 2 4 4 2020-21 Jokerit Helsinki KHL 57 8 6 14 44 -1 4 0 0 0 14 2021-22 Jokerit Helsinki KHL 9 2 0 2 0 2 Jonas Enlund Center -- shoots L Born Nov 3 1987 -- Helsinki, Finland [33 years ago] Height 6.00 -- Weight 209 Drafted by Atlanta Thrashers round 6 #165 overall 2006 NHL Entry Draft Regular Season Playoffs Season Team League -

Dallas Stars Game Notes
Dallas Stars Game Notes Sat, Mar 27, 2021 NHL Game #538 Dallas Stars 11 - 11 - 8 (30 pts) Florida Panthers 20 - 9 - 4 (44 pts) Team Game: 31 7 - 5 - 6 (Home) Team Game: 34 10 - 4 - 3 (Home) Home Game: 19 4 - 6 - 2 (Road) Road Game: 17 10 - 5 - 1 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 29 Jake Oettinger 16 5 2 6 2.28 .912 60 Chris Driedger 14 8 4 2 2.28 .923 35 Anton Khudobin 17 6 9 2 2.45 .910 72 Sergei Bobrovsky 19 12 5 2 2.92 .902 41 Landon Bow - - - - - - # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 2 D Jamie Oleksiak 30 3 5 8 2 27 3 D Keith Yandle 33 3 16 19 -6 30 3 D John Klingberg 29 5 15 20 -4 17 5 D Aaron Ekblad 33 10 10 20 2 31 4 D Miro Heiskanen 30 4 12 16 1 6 7 D Radko Gudas 32 0 5 5 11 25 5 D Andrej Sekera 23 2 1 3 5 4 10 R Brett Connolly 17 1 2 3 4 0 10 C Ty Dellandrea 19 3 2 5 4 14 11 L Jonathan Huberdeau 33 11 25 36 -4 18 11 C Andrew Cogliano 28 3 4 7 3 11 13 C Vinnie Hinostroza 9 0 0 0 -2 0 12 C Radek Faksa 30 4 6 10 -3 12 16 C Aleksander Barkov 31 13 24 37 11 6 13 D Mark Pysyk 21 1 0 1 4 14 19 L Mason Marchment 16 2 4 6 2 8 14 L Jamie Benn 26 5 10 15 7 25 21 C Alex Wennberg 33 7 8 15 -2 8 15 L Blake Comeau 25 1 6 7 0 4 23 C Carter Verhaeghe 33 12 12 24 14 23 16 C Joe Pavelski 30 15 17 32 11 8 27 C Eetu Luostarinen 32 3 5 8 -6 10 17 R Nick Caamano 21 0 1 1 -6 17 42 D Gustav Forsling 20 2 3 5 0 4 18 C Jason Dickinson 30 5 4 9 -3 12 52 D MacKenzie Weegar 33 2 17 19 10 37 21 L Jason Robertson 25 5 15 20 5 8 55 C Noel Acciari 25 3 5 8 1 2 23 D Esa Lindell 30 3 4 7 2 10 61 D Riley Stillman 1 -

2019-20 UD the Cup Hockey Checklist Upper Deck
2019/20 The Cup Hockey Group Break Checklist Green = Autograph or Relic; White = Insert/Base Player Set Card # Team Print Run Anton Stastny Auto - Enshrinements E-AS Avalanche 99 Cale Makar Auto - 2019-20 Upper Deck Print Plate Booklets - Young Guns 493 Avalanche 1 Cale Makar Auto - 9-Way Signatures Booklets 9W-RC Avalanche 9 Cale Makar Auto - Base Black Foil Rookie 62 Avalanche 1 Cale Makar Auto - Base Gold Spectrum Foil Rookie 62 Avalanche 24 Cale Makar Auto - Brilliance B-CM Avalanche Cale Makar Auto - Color Coded - Rookies CC-CM Avalanche 33 Cale Makar Auto - Enshrinements - Rookies E-CM Avalanche 99 Cale Makar Auto - Inked Insignias MF Patch II-CM Avalanche 75 Cale Makar Auto - NHL Glory Metal Shield G-CM Avalanche 10 Cale Makar Auto - Rookie Class of 2020 Foil Parallels 2020-CM Avalanche 81 Cale Makar Auto - Rookie Plate - Exquisite RPA EC-CM Avalanche 4 Cale Makar Auto - Rookie Plate - SP Authentic Future Watch 149 Avalanche 4 Cale Makar Auto - Rookie Plate - Stature 124 Avalanche 4 Cale Makar Auto - Rookie Plate - The Cup 62 Avalanche 4 Cale Makar Auto - Rookie Plate - UD Black Lustrous RPA LR-CM Avalanche 4 Cale Makar Auto - Rookie Plate - UD Premier Acetate AR-CM Avalanche 4 Cale Makar Auto - Rookie Plate - Ultimate Rookies 190 Avalanche 4 Cale Makar Auto - Signature Renditions SR-CM Avalanche Cale Makar Auto - Top Ten Pick + Parallel 2017-4 Avalanche 5 Cale Makar Auto Relic - 2019-20 Splendor - Rookies SP-MA Avalanche 36 Cale Makar Auto Relic - Base Auto Patch Gold Rookie 62 Avalanche 12 Cale Makar Auto Relic - Base Green Foil -

Tampa Bay Lightning Playoff Game Notes
Tampa Bay Lightning Playoff Game Notes Sat, Sep 19, 2020 Round 4 Game 1 Tampa Bay Lightning 14 - 5 - 1 Dallas Stars 13 - 8 - 0 Team Game: 20 7 - 4 - 1 (Home) Team Game: 22 5 - 4 - 0 (Home) Home Game: 12 7 - 1 - 0 (Road) Road Game: 13 8 - 4 - 0 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 29 Scott Wedgewood - - - - - - 29 Jake Oettinger 1 0 0 0 0.00 1.00 35 Curtis McElhinney - - - - - - 0 88 Andrei Vasilevskiy 19 14 5 0 1.82 .931 30 Ben Bishop 3 1 2 0 5.43 .844 35 Anton Khudobin 19 12 6 0 2.62 .920 41 Landon Bow - - - - - - # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 2 D Luke Schenn 10 0 2 2 3 7 2 D Jamie Oleksiak 21 4 3 7 5 18 7 R Mathieu Joseph - - - - - - 3 D John Klingberg 20 3 13 16 -2 8 9 C Tyler Johnson 19 4 3 7 -5 11 4 D Miro Heiskanen 21 5 17 22 3 2 13 C Cedric Paquette 19 0 2 2 -2 12 5 D Andrej Sekera 21 0 1 1 -2 0 14 L Pat Maroon 19 1 3 4 4 6 10 R Corey Perry 21 2 4 6 -5 21 17 L Alex Killorn 18 4 4 8 -3 27 11 C Andrew Cogliano 17 0 1 1 -4 6 18 L Ondrej Palat 19 8 5 13 14 4 12 C Radek Faksa 19 3 5 8 -3 4 19 C Barclay Goodrow 19 1 4 5 6 14 13 C Mattias Janmark 20 0 5 5 0 34 20 C Blake Coleman 19 4 6 10 5 27 14 L Jamie Benn 21 8 10 18 0 18 21 C Brayden Point 17 9 16 25 13 8 15 L Blake Comeau 21 2 4 6 -3 26 22 D Kevin Shattenkirk 19 1 8 9 11 4 16 C Joe Pavelski 21 9 5 14 2 24 23 C Carter Verhaeghe 5 0 2 2 1 0 17 R Nick Caamano - - - - - - 24 D Zach Bogosian 18 0 4 4 2 12 18 C Jason Dickinson 21 0 2 2 -7 6 27 D Ryan McDonagh 16 1 4 5 -3 6 21 L Jason Robertson - - - - - - 37 C Yanni Gourde 19 5 7 12 12 -

Dallas Stars Playoff Game Notes
Dallas Stars Playoff Game Notes Thu, Aug 13, 2020 Round 1 Game 2 Dallas Stars 1 - 3 - 0 Calgary Flames 4 - 1 - 0 Team Game: 5 0 - 2 - 0 (Home) Team Game: 6 1 - 1 - 0 (Home) Home Game: 3 1 - 1 - 0 (Road) Road Game: 4 3 - 0 - 0 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 29 Jake Oettinger - - - - - - 32 Jon Gillies - - - - - - 30 Ben Bishop 1 0 1 0 4.07 .875 33 David Rittich - - - - - - 35 Anton Khudobin 3 1 2 0 2.62 .909 39 Cam Talbot 5 4 1 0 1.61 .941 41 Landon Bow - - - - - - 50 Artyom Zagidulin - - - - - - # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 2 D Jamie Oleksiak 4 1 1 2 1 0 4 D Rasmus Andersson 5 2 0 2 6 4 3 D John Klingberg 3 0 1 1 -2 2 5 D Mark Giordano 5 0 1 1 0 4 4 D Miro Heiskanen 4 0 5 5 0 2 7 D TJ Brodie 5 0 1 1 1 4 5 D Andrej Sekera 4 0 0 0 -4 0 8 D Juuso Valimaki - - - - - - 10 R Corey Perry 4 1 0 1 -2 9 10 C Derek Ryan 5 0 1 1 1 0 11 C Andrew Cogliano 4 0 0 0 0 2 11 C Mikael Backlund 5 2 2 4 2 4 12 C Radek Faksa 4 0 0 0 -1 0 13 L Johnny Gaudreau 5 2 1 3 2 0 13 C Mattias Janmark 4 0 1 1 0 4 16 C Tobias Rieder 5 1 1 2 1 0 14 L Jamie Benn 4 1 0 1 -4 0 17 L Milan Lucic 5 1 4 5 2 11 15 L Blake Comeau 4 0 1 1 -1 0 19 L Matthew Tkachuk 5 1 1 2 3 10 16 C Joe Pavelski 4 2 0 2 -2 0 20 D Derek Forbort 5 0 1 1 4 2 17 R Nick Caamano - - - - - - 23 C Sean Monahan 5 2 4 6 4 0 18 C Jason Dickinson 4 0 0 0 -2 0 26 D Michael Stone - - - - - - 21 L Jason Robertson - - - - - - 27 C Austin Czarnik - - - - - - 23 D Esa Lindell 4 0 1 1 -5 2 28 C Elias Lindholm 5 2 1 3 2 0 24 L Roope Hintz 4 0 1 1 0 2 29 C Dillon -

Francis Benedict Pecoskie Memorial Foundation Hockey Pool 2020 Stanley Cup Qualifiers and Playoffs
Francis Benedict Pecoskie Memorial Foundation Hockey Pool 2020 Stanley Cup Qualifiers and Playoffs RULES Prizes: 1st Place - $500.00 2nd Place -$300.00 3rd Place - $100.00 Cost: $20.00 per team - You may enter as many teams as you wish - Money must accompany your entry Scoring: · Each goal or assist counts for 1 point · Points count beginning August 1st with the Best of 5 qualification round AND the top 8 seeds' round robin games · The person with the team that accumulates the most points throughout the 2020 Stanley Cup tournament, wins · All pool data will be entered into Officepools this year. Once it is entered/accessible, a link and login information will be posted at: https://www.fbpmemorial.ca Ties: If, at the end of the playoffs, pool teams are tied in the standings the winner(s) will be determined using the following criteria. The steps will be followed in order until a winner is determined. 1. The team with the most goals 2. The team with the most players in the Stanley Cup Finals 3. The team with the most defencemen 4. The team with the most game winning goals 5. If still tied, the teams will split the winnings equally DEADLINE: All entries (second page front & back) must be returned no later than 11:59PM EST, Friday July 31st 2020 - Printed entries may be returned to seller or electronic entries may be submitted to [email protected] with accompanying etransfer. Team Selection: 1. To make your team, select 20 (twenty) players from the attached list by placing an (X) in the box beside the player’s name. -

Dallas Stars Game Notes
Dallas Stars Game Notes Sat, Apr 10, 2021 NHL Game #648 Dallas Stars 14 - 14 - 10 (38 pts) Florida Panthers 26 - 11 - 4 (56 pts) Team Game: 39 7 - 6 - 7 (Home) Team Game: 42 14 - 4 - 3 (Home) Home Game: 21 7 - 8 - 3 (Road) Road Game: 21 12 - 7 - 1 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 29 Jake Oettinger 20 6 5 6 2.29 .917 30 Spencer Knight - - - - - - 35 Anton Khudobin 21 8 9 4 2.40 .912 60 Chris Driedger 18 11 5 2 2.05 .930 41 Landon Bow - - - - - - 72 Sergei Bobrovsky 23 15 6 2 2.80 .910 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 2 D Jamie Oleksiak 38 3 5 8 1 31 3 D Keith Yandle 41 3 18 21 -7 32 3 D John Klingberg 37 6 19 25 -11 21 6 D Anton Stralman 33 3 6 9 -4 6 4 D Miro Heiskanen 38 6 15 21 -2 8 7 D Radko Gudas 40 0 5 5 8 27 5 D Andrej Sekera 30 2 2 4 5 4 8 D Matt Kiersted 4 0 0 0 -1 2 10 C Ty Dellandrea 25 3 2 5 0 23 11 L Jonathan Huberdeau 41 14 28 42 -3 24 11 C Andrew Cogliano 36 5 5 10 3 13 16 C Aleksander Barkov 35 16 26 42 12 8 12 C Radek Faksa 37 5 7 12 -2 18 19 L Mason Marchment 24 2 6 8 6 14 13 D Mark Pysyk 26 1 1 2 6 16 21 C Alex Wennberg 41 11 8 19 1 8 14 L Jamie Benn 34 7 13 20 2 25 23 C Carter Verhaeghe 41 17 18 35 23 27 15 L Blake Comeau 33 3 10 13 2 10 25 D Brady Keeper 1 0 0 0 0 0 16 C Joe Pavelski 38 15 20 35 10 8 27 C Eetu Luostarinen 40 3 5 8 -8 12 17 R Nick Caamano 23 0 1 1 -6 17 42 D Gustav Forsling 28 3 6 9 9 6 18 C Jason Dickinson 35 5 5 10 -3 12 52 D MacKenzie Weegar 41 3 21 24 21 39 21 L Jason Robertson 33 9 16 25 7 10 55 C Noel Acciari 33 4 7 11 4 4 23 D Esa Lindell 38