Decathlon Rules: an Axiomatic Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Weight Pentathlon Shall Be Included in the Team Events
EVAA TECHNICAL MANAGER WMA STADIA COMMITTEE MEMBER Dear athletes-Affiliates At the general assembly in san Sebastian there will be several point that will be raised regarding competition, as I am aware that many of the affiliates may not attend the assembly I would appreciate your feedback on some of the points raised in the following series of possible proposals. Even when you will have members attending it would be good for me to have some of your ideas as to these things, so that though I may be for or against them I have some feedback from my region, please mail me your comments and I will make a list for the meeting in August. Winston Thomas. [email protected] Possible Team medals in the Weight Pentathlon PROPOSAL The Weight Pentathlon shall be included in the team events, Team medal shall be awarded in the Weight Pentathlon. Awards will be for Women and men *M35 upwards in 5 year age groups Teams will consist of there scoring athlete Their total scores will be added to secure the final points. Athlete will be able to score in a lower age class only where they have no team in their own age group and all the implements are of the same specifications. For a trial period of 1 championships teams shall pay a €6.00 entry fee Teams will be free from this period as with other team events. *Note M35 should they be adopted by WMA/IAAF Ruling to be added in THE COMPETITION Field Events 12.(6) When team competitions are included in Weight pentathlon, there shall be three team awards on the basis that each Affiliate is entitled to count one team (best three to score) in five year age groups, and their results shall be computed on the points gained. -

A Mathematical Analysis of the 4 X 100 M Relay
Journal of Sports Sciences, 2002, 20, 369± 381 A mathematical analysis of the 4 ´ 100 m relay A.J. WARD-SMITH and P.F. RADFORD* Department of Sport Sciences, Brunel University, Osterley Campus, Borough Road, Isleworth, Middlesex TW7 5DU, UK Accepted 19 November 2001 In this study, we examined aspects of the 4 ´ 100 m relay that are amenable to mathematical analysis. We looked at factors that aþ ect the time required to complete the relay, focusing on the performance of elite male athletes. Factors over which the individual athletes, and the team coach, can exercise some control are: the starting positions of the runners on legs 2, 3 and 4, the positions at which baton exchanges occur, the free distances at the baton exchanges and the running order of the athletes. The lane draw is shown to have an important in¯ uence on the relay time, although it is outside the control of the team coach. Teams drawn in the outside lanes bene® t from the inverse relation between bend radius of curvature and running speed. For teams composed of athletes with diþ erent times over 100 m, we show that the fastest relay times are achieved with the fastest athlete taking the ® rst leg, with the slowest two runners allocated to the ® nal two legs. Keywords: athletics, running, sprinting. Introduction allowance is made for bend curvature in the layout of the starting lines, which are staggered across the eight The aim of this study was to examine aspects of the lanes of the track. These rules eþ ectively determine the 4 ´ 100 m relay that are amenable to mathematical distances run by the runners on each of the four legs. -

Success on the World Stage Athletics Australia Annual Report 2010–2011 Contents
Success on the World Stage Athletics Australia Annual Report Success on the World Stage Athletics Australia 2010–2011 2010–2011 Annual Report Contents From the President 4 From the Chief Executive Officers 6 From The Australian Sports Commission 8 High Performance 10 High Performance Pathways Program 14 Competitions 16 Marketing and Communications 18 Coach Development 22 Running Australia 26 Life Governors/Members and Merit Award Holders 27 Australian Honours List 35 Vale 36 Registration & Participation 38 Australian Records 40 Australian Medalists 41 Athletics ACT 44 Athletics New South Wales 46 Athletics Northern Territory 48 Queensland Athletics 50 Athletics South Australia 52 Athletics Tasmania 54 Athletics Victoria 56 Athletics Western Australia 58 Australian Olympic Committee 60 Australian Paralympic Committee 62 Financial Report 64 Chief Financial Officer’s Report 66 Directors’ Report 72 Auditors Independence Declaration 76 Income Statement 77 Statement of Comprehensive Income 78 Statement of Financial Position 79 Statement of Changes in Equity 80 Cash Flow Statement 81 Notes to the Financial Statements 82 Directors’ Declaration 103 Independent Audit Report 104 Trust Funds 107 Staff 108 Commissions and Committees 109 2 ATHLETICS AuSTRALIA ANNuAL Report 2010 –2011 | SuCCESS ON THE WORLD STAGE 3 From the President Chief Executive Dallas O’Brien now has his field in our region. The leadership and skillful feet well and truly beneath the desk and I management provided by Geoff and Yvonne congratulate him on his continued effort to along with the Oceania Council ensures a vast learn the many and numerous functions of his array of Athletics programs can be enjoyed by position with skill, patience and competence. -

Lesson Plans Introduction the Following Section Provides Twenty-Seven Ready-To-Implement Lesson Plans for Teachers
Lesson Plans Introduction The following section provides twenty-seven ready-to-implement lesson plans for teachers. The section is divided into four smaller sub-sections. • Early Stage 1 (5 year olds) • Stage 1 (6/7 year olds) • Stage 2 (8/9 year olds) • Stage 3 (10 years and LAANSWabove) ASAP Level 3 Each sub-section contains lesson plans suitable for children in these age groups. The lesson plans assume classes of up to thirty students and a time limit of 30-45 minutes, however a teacher can adapt the ideas to suit their particular circumstances. Each lesson plan generally follows the same format, being: Aim; Equipment; Warm Up; Skill Development; Games. In relevant places, topics such as safety aspects and various hints that will help the teacher organise and conduct a successful lesson are included. The lesson plans at times assume prior learning, ie. that the children have participated in the skill development activities contained in preceding lessons designed for the earlier levels. The activities featured in the lesson plans are based on fun, skill development, maximum group participation and a sound, logical progression. The lesson plans form the foundation of a class athletics unit. 3 29 Early Stage 1 Lesson Plans • Running - Lesson 1 - Lesson 2 • Jumping - Lesson 1 - LessonLAANSW 2 ASAP Level 3 • Throwing - Lesson 1 - Lesson 2 30 Early Stage 1 Running Lesson Plan Lesson 1 Introduction to basic running technique Introduction to relays Ground markers x 30 Relay batons x 5 Warm Up 1. Group Game: "Signals" LAANSW ASAP Level 3 Set up a playing area with ground markers. -

Athletics, Badminton, Gymnastics, Judo, Swimming, Table Tennis, and Wrestling
INDIVIDUAL GAMES 4 Games and sports are important parts of our lives. They are essential to enjoy overall health and well-being. Sports and games offer numerous advantages and are thus highly recommended for everyone irrespective of their age. Sports with individualistic approach characterised with graceful skills of players are individual sports. Do you like the idea of playing an individual sport and be responsible for your win or loss, success or failure? There are various sports that come under this category. This chapter will help you to enhance your knowledge about Athletics, Badminton, Gymnastics, Judo, Swimming, Table Tennis, and Wrestling. ATHLETICS Running, jumping and throwing are natural and universal forms of human physical expression. Track and field events are the improved versions of all these. These are among the oldest of all sporting competitions. Athletics consist of track and field events. In the track events, competitions of races of different distances are conducted. The different track and field events have their roots in ancient human history. History Ancient Olympic Games are the first recorded examples of organised track and field events. In 776 B.C., in Olympia, Greece, only one event was contested which was known as the stadion footrace. The scope of the games expanded in later years. Further it included running competitions, but the introduction of the Ancient Olympic pentathlon marked a step towards track and field as it is recognised today. There were five events in pentathlon namely—discus throw, long jump, javelin throw, the stadion foot race, and wrestling. 2021-22 Chap-4.indd 49 31-07-2020 15:26:11 50 Health and Physical Education - XI Track and field events were also present at the Pan- Activity 4.1 Athletics at the 1960 Summer Hellenic Games in Greece around 200 B.C. -
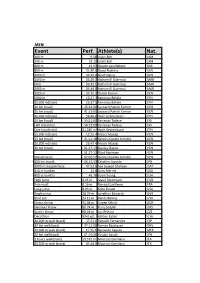
Event Perf. Athlete(S) Nat
MEN Event Perf. Athlete(s) Nat. 100 m 9.58 Usain Bolt JAM 200 m 19.19 Usain Bolt JAM 400 m 43.03 Wayde van Niekerk RSA 800 m 01:40.9 David Rudisha KEN 1000 m 02:12.0 Noah Ngeny KEN 1500 m 03:26.0 Hicham El Guerrouj MAR Mile 03:43.1 Hicham El Guerrouj MAR 2000 m 04:44.8 Hicham El Guerrouj MAR 3000 m 07:20.7 Daniel Komen KEN 5000 m 12:37.4 Kenenisa Bekele ETH 10,000 m(track) 26:17.5 Kenenisa Bekele ETH 10 km (road) 26:44:00 Leonard Patrick Komon KEN 15 km (road) 41:13:00 Leonard Patrick Komon KEN 20,000 m(track) 56:26.0 Haile Gebrselassie ETH 20 km (road) 55:21:00 Zersenay Tadese ERI Half marathon 58:23:00 Zersenay Tadese ERI One hour(track) 21,285 m Haile Gebrselassie ETH 25,000 m(track) 12:25.4 Moses Mosop KEN 25 km (road) 01:11:18 Dennis Kipruto Kimetto KEN 30,000 m(track) 26:47.4 Moses Mosop KEN 30 km (road) 01:27:13 Stanley Biwott KEN 01:27:13 Eliud Kipchoge KEN Marathon[a] 02:02:57 Dennis Kipruto Kimetto KEN 100 km (road) 06:13:33 Takahiro Sunada JPN 3000 m steeplechase 07:53.6 Saif Saaeed Shaheen QAT 110 m hurdles 12.8 Aries Merritt USA 400 m hurdles 46.78 Kevin Young USA High jump 2.45 m Javier Sotomayor CUB Pole vault 6.16 m Renaud Lavillenie FRA Long jump 8.95 m Mike Powell USA Triple jump 18.29 m Jonathan Edwards GBR Shot put 23.12 m Randy Barnes USA Discus throw 74.08 m Jürgen Schult GDR Hammer throw 86.74 m Yuriy Sedykh URS Javelin throw 98.48 m Jan Železný CZE Decathlon 9045 pts Ashton Eaton USA 10,000 m walk (track) 37:53.1 Paquillo Fernández ESP 10 km walk(road) 37:11:00 Roman Rasskazov RUS 20,000 m walk (track) 17:25.6 Bernardo -

Standard Tables 2020 E.S.A.A
Standard Tables 2020 E.S.A.A. National Standards are those performance levels for which standard badges may be purchased at the National Championships. Entry Standards are the minimum performance levels normally required for an athlete to be selected for a County Team for the National Championships. County Standards correspond to a good standard of performance by an athlete competing in a County Championship meeting. District Standard corresponds to a good standard of performance by an athlete competing at a District Championship meeting. These may need amendment to suit the variations in type of District Championship staged. School Standard corresponds to a good standard of performance by an athlete competing at a School Championship meeting. Except for Year 7 and 8 tables - the age groups, events and event specifications are as set out in the Track and Field Competition Rules. Years 7 and 8 The variety of events and specifications is offered in order to cater for the intense athletic interest and for the rapid physical changes which take place at this stage. It is stressed that success in the initial teaching of athletics stems from the understanding that the physical challenge to the pupil should not exceed that which can be comfortably handled. All children, therefore, should be started with light implements and low hurdles, and be allowed to progress as appropriate to themselves. This will almost certainly create some problems of organisation at school level, but these are NOT insurmountable. The Standards shown for younger age groups and for School and District level are being re-worked to match the Awards Scheme. -

Edwards Stadium
The University of California, Berkeley Edwards Stadium Historic structure report The University of California, Berkeley Edwards Stadium HISTORIC STRUCTURE REPORT Contents IntroductIon .................................................................................07 descrIptIon & condItIons assessment ...................65 purpose and scope ................................................................. 10 site and Landscape .................................................................66 subject of this study ............................................................. 10 Landscape Around the stadium .......................................67 Methodology .................................................................................11 Landscape inside the stadium ..........................................75 exterior Description ................................................................78 HIstorIcal context ..................................................................17 interior Description ..................................................................87 early History of Berkeley: 1820-1859 ...............................18 Materials and Features ...........................................................92 college of california: 1860-1868 ........................................19 condition ......................................................................................99 early physical Development of the Berkeley campus ..................................................................... 20 analysIs of HIstorIcal -

Model Function of Women's 1500M World Record Improvement Over Time
Undergraduate Journal of Mathematical Modeling: One + Two Volume 8 | 2018 Spring 2018 Article 3 2018 Model Function of Women’s 1500m World Record Improvement over Time Annie Allmark University of South Florida Advisors: Arcadii Grinshpan, Mathematics and Statistics Waren Bye, USF Athletics Department, Track and Field Head Coach Problem Suggested By: Annie Allmark Follow this and additional works at: https://scholarcommons.usf.edu/ujmm Part of the Mathematics Commons UJMM is an open access journal, free to authors and readers, and relies on your support: Donate Now Recommended Citation Allmark, Annie (2018) "Model Function of Women’s 1500m World Record Improvement over Time," Undergraduate Journal of Mathematical Modeling: One + Two: Vol. 8: Iss. 2, Article 3. DOI: http://doi.org/10.5038/2326-3652.8.2.4890 Available at: https://scholarcommons.usf.edu/ujmm/vol8/iss2/3 Model Function of Women’s 1500m World Record Improvement over Time Abstract We give an example of simple modeling of the known sport results that can be used for athletes’ self- improvement and estimation of future achievements. This project compares the women’s 1500-meter world record times to the time elapsed between when they were run. The function of time which describes this comparison is found through graphing the data and interpreting the graphs. Then the obtained model function is compared to the real time data. The conclusions drawn from the result include that the calculated function of time lacks in accuracy as time elapsed increases, but the model could be used to estimate the future world records. Keywords track and field, running, exponential modeling, line of best fit Creative Commons License This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 License. -

Athletics SA 2021 State Track and Field Championships
Athletics SA 2021 State Track and Field Championships Final Timetable - as at 25/2/2021 Friday - 26th February Day Time Event Age Group Round Long Jump Triple Jump High Jump Pole Vault Shot Put Discus Javelin Hammer Fri 6.30 PM 3000 metres Walk Under 14 Men & Women FINAL 6.30 PM U17/18/20 Women Fri 3000 metres Walk Under 15 Men & Women FINAL Fri 3000 metres Walk Under 16 Men & Women FINAL Fri 5000 metres Walk Under 17 Men & Women FINAL 6.35 PM U17/18/20 Women Fri 5000 metres Walk Under 18 Men & Women FINAL Fri 5000 metres Walk Under 20 Women FINAL Fri 5000 metres Walk Under Open Women FINAL Fri 5000 metres Walk Under 20 Men FINAL Fri 5000 metres Walk Under Open Men FINAL Fri 5000 metres Walk Over 35 & Over 50 Men & FINAL 6.40 PM Women U14/15/16 Men Fri 6.45 PM 6.45 PM U15/16/U20 Women Fri 6.50 PM 6.50 PM Fri 6.55 PM 6.55 PM Fri 7.00 PM 200 metres Hurdles Under 15 Women FINAL 7.00 PM Fri 200 metres Hurdles Under 16 Women FINAL Fri 7.05 PM 200 metres Hurdles Under 15 Men FINAL 7.05 PM Fri 200 metres Hurdles Under 16 Men FINAL Fri 7.10 PM 200 metres Hurdles Over 35 & Over 50 Men & FINAL 7.10 PM Women Fri 7.15 PM 7.15 PM O35/O50 Women Fri 7.20 PM 400 metres Hurdles Open Men FINAL 7.20 PM Fri 400 metres Hurdles Under 20 Men FINAL 7.25 PM Fri 7:30 PM 400 metres Hurdles Under 17 Men FINAL 7.30 PM Fri 400 metres Hurdles Under 18 Men FINAL Fri 7.35 PM 7.35 PM Open Women Fri 7:40 PM 400 metres Hurdles Under 17 Women FINAL 7.40 PM Seated Fri 400 metres Hurdles Under 18 Women FINAL 7.45 PM U17/18/20 Men U17/18/20 Men Fri 7.50 PM 800 metres Open Men -

A Proposal to Change the Women's Hurdles Events by Sergio Guarda
VIEWPOINT Ptrgi -i^^ by l/V\F 8:2; 23-26. 1993 A proposal to change the 1 Introduction women's hurdles events The Sprint hurdles race, more or less, as we now know it. was 'invented' at Oxford University in 1864. The dislance was 12(1 by Sergio Guarda Etcheverry yards, with an approach and finish of 15 yards and a 10 yards spacing between 10 hurdles, 3 foot 6 inches in height. These measurements formed the basis for the event when it was included in the firsi modern Olympic Games, held at Athens in 1896. There, measurements became the metric equivalents. 1 Ul metres dislance. 10 hurdles 106.7cm in height and 9.14 metres apart, a dislance from starl line lo first hurdle of 13.72 metres and from lasl hurdle to finish of 14.02 meires. The first gold medal for the Olympic event was won by Thomas Curtis (USA) wilh a lime of 17 •V5 sec. From thai dale to the present, the rules of this event have noi been modified despite the progress made in lhe construc tion of the hurdles, in the quality of the track surface, in the quality of the shoes, in the selection of lhe athletes and in the spe cific training methodology and planning. Thc 400 metres Hurdles for men was incorporated in the programme for lhe Sergio Guarda Etcheverry is a professor 1900 Olympic Games, held in Paris. The of phvsical education al the Ufiivcisiiy of winner on this firsl occasion was Waller Santiago. Chile, andanteinberofihe Tewksbury (USA) with a time of 57.6 sec. -

HEEL and TOE ONLINE the Official Organ of the Victorian Race Walking
HEEL AND TOE ONLINE The official organ of the Victorian Race Walking Club 2019/2020 Number 40 Tuesday 30 June 2020 VRWC Preferred Supplier of Shoes, clothes and sporting accessories. Address: RUNNERS WORLD, 598 High Street, East Kew, Victoria (Melways 45 G4) Telephone: 03 9817 3503 Hours: Monday to Friday: 9:30am to 5:30pm Saturday: 9:00am to 3:00pm Website: http://www.runnersworld.com.au Facebook: http://www.facebook.com/pages/Runners-World/235649459888840 VRWC COMPETITION RESTARTS THIS SATURDAY Here is the big news we have all been waiting for. Our VRWC winter roadwalking season will commence on Saturday afternoon at Middle Park. Club Secretary Terry Swan advises the the club committee meet tonight (Tuesday) and has given the green light. There will be 3 Open races as follows VRWC Roadraces, Middle Park, Saturday 6th July 1:45pm 1km Roadwalk Open (no timelimit) 2.00pm 3km Roadwalk Open (no timelimit) 2.30pm 10km Roadwalk Open (timelimit 70 minutes) Each race will be capped at 20 walkers. Places will be allocated in order of entry. No exceptions can be made for late entries. $10 per race entry. Walkers can only walk in ONE race. Multiple race entries are not possible. Race entries close at 6PM Thursday. No entries will be allowed on the day. You can enter in one of two ways • Online entry via the VRWC web portal at http://vrwc.org.au/wp1/race-entries-2/race-entry-sat-04jul20/. We prefer payment by Credit Card or Paypal within the portal when you register. Ignore the fact that the portal says entries close at 10PM on Wednesday.