Automated Study of Isoptic Curves: a New Approach with Geogebra∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Orthocorrespondence and Orthopivotal Cubics
Forum Geometricorum b Volume 3 (2003) 1–27. bbb FORUM GEOM ISSN 1534-1178 Orthocorrespondence and Orthopivotal Cubics Bernard Gibert Abstract. We define and study a transformation in the triangle plane called the orthocorrespondence. This transformation leads to the consideration of a fam- ily of circular circumcubics containing the Neuberg cubic and several hitherto unknown ones. 1. The orthocorrespondence Let P be a point in the plane of triangle ABC with barycentric coordinates (u : v : w). The perpendicular lines at P to AP , BP, CP intersect BC, CA, AB respectively at Pa, Pb, Pc, which we call the orthotraces of P . These orthotraces 1 lie on a line LP , which we call the orthotransversal of P . We denote the trilinear ⊥ pole of LP by P , and call it the orthocorrespondent of P . A P P ∗ P ⊥ B C Pa Pc LP H/P Pb Figure 1. The orthotransversal and orthocorrespondent In barycentric coordinates, 2 ⊥ 2 P =(u(−uSA + vSB + wSC )+a vw : ··· : ···), (1) Publication Date: January 21, 2003. Communicating Editor: Paul Yiu. We sincerely thank Edward Brisse, Jean-Pierre Ehrmann, and Paul Yiu for their friendly and valuable helps. 1The homography on the pencil of lines through P which swaps a line and its perpendicular at P is an involution. According to a Desargues theorem, the points are collinear. 2All coordinates in this paper are homogeneous barycentric coordinates. Often for triangle cen- ters, we list only the first coordinate. The remaining two can be easily obtained by cyclically permut- ing a, b, c, and corresponding quantities. Thus, for example, in (1), the second and third coordinates 2 2 are v(−vSB + wSC + uSA)+b wu and w(−wSC + uSA + vSB )+c uv respectively. -

Generalization of the Pedal Concept in Bidimensional Spaces. Application to the Limaçon of Pascal• Generalización Del Concep
Generalization of the pedal concept in bidimensional spaces. Application to the limaçon of Pascal• Irene Sánchez-Ramos a, Fernando Meseguer-Garrido a, José Juan Aliaga-Maraver a & Javier Francisco Raposo-Grau b a Escuela Técnica Superior de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Madrid, España. [email protected], [email protected], [email protected] b Escuela Técnica Superior de Arquitectura, Universidad Politécnica de Madrid, Madrid, España. [email protected] Received: June 22nd, 2020. Received in revised form: February 4th, 2021. Accepted: February 19th, 2021. Abstract The concept of a pedal curve is used in geometry as a generation method for a multitude of curves. The definition of a pedal curve is linked to the concept of minimal distance. However, an interesting distinction can be made for . In this space, the pedal curve of another curve C is defined as the locus of the foot of the perpendicular from the pedal point P to the tangent2 to the curve. This allows the generalization of the definition of the pedal curve for any given angle that is not 90º. ℝ In this paper, we use the generalization of the pedal curve to describe a different method to generate a limaçon of Pascal, which can be seen as a singular case of the locus generation method and is not well described in the literature. Some additional properties that can be deduced from these definitions are also described. Keywords: geometry; pedal curve; distance; angularity; limaçon of Pascal. Generalización del concepto de curva podal en espacios bidimensionales. Aplicación a la Limaçon de Pascal Resumen El concepto de curva podal está extendido en la geometría como un método generativo para multitud de curvas. -

HYPERBOLA HYPERBOLA a Conic Is Said to Be a Hyperbola If Its Eccentricity Is Greater Than One
HYPERBOLA HYPERBOLA A Conic is said to be a hyperbola if its eccentricity is greater than one. If S ax22 hxy by 2 2 gx 2 fy c 0 represents a hyperbola then h2 ab 0 and 0 2 2 If S ax2 hxy by 2 gx 2 fy c 0 represents a rectangular hyperbola then h2 ab 0 , 0 and a b 0 x2 y 2 Hyperbola: Equation of the hyperbola in standard form is 1. a2 b2 Hyperbola is symmetric about both the axes. Hyperbola does not passing through the origin and does not meet the Y - axis. Hyperbola curve does not exist between the lines x a and x a . x2 y 2 xx yy x2 y 2 x x y y Notation: S 1 , S1 1 1, S1 1 1, S1 2 1 2 1. a2 b 2 1 a2 b 2 11 a2 b 2 12 a2 b 2 Rectangular hyperbola (or) Equilateral hyperbola : In a hyperbola if the length of the transverse axis (2a) is equal to the length of the conjugate axis (2b) , then the hyperbola is called a rectangular hyperbola or an equilateral hyperbola. The eccentricity of a rectangular hyperbola is 2 . Conjugate hyperbola : The hyperbola whose transverse and conjugate axes are respectively the conjugate and transverse axes of a given hyperbola is called the conjugate hyperbola of the given hyperbola. 2 2 1 x y The equation of the hyperbola conjugate to S 0 is S 1 0 . a2 b 2 If e1 and e2 be the eccentricities of the hyperbola and its conjugate hyperbola then 1 1 2 2 1. -

Elementary Euclidean Geometry an Introduction
Elementary Euclidean Geometry An Introduction C. G. GIBSON PUBLISHED BY THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE The Pitt Building, Trumpington Street, Cambridge, United Kingdom CAMBRIDGE UNIVERSITY PRESS The Edinburgh Building, Cambridge CB2 2RU, UK 40 West 20th Street, New York, NY 10011–4211, USA 477 Williamstown Road, Port Melbourne, VIC 3207, Australia Ruiz de Alarcon´ 13, 28014 Madrid, Spain Dock House, The Waterfront, Cape Town 8001, South Africa http://www.cambridge.org C Cambridge University Press 2003 This book is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published 2003 Printed in the United Kingdom at the University Press, Cambridge Typeface Times 10/13 pt. System LATEX2ε [TB] A catalogue record for this book is available from the British Library Library of Congress Cataloguing in Publication data ISBN 0 521 83448 1 hardback Contents List of Figures page viii List of Tables x Preface xi Acknowledgements xvi 1 Points and Lines 1 1.1 The Vector Structure 1 1.2 Lines and Zero Sets 2 1.3 Uniqueness of Equations 3 1.4 Practical Techniques 4 1.5 Parametrized Lines 7 1.6 Pencils of Lines 9 2 The Euclidean Plane 12 2.1 The Scalar Product 12 2.2 Length and Distance 13 2.3 The Concept of Angle 15 2.4 Distance from a Point to a Line 18 3 Circles 22 3.1 Circles as Conics 22 3.2 General Circles 23 3.3 Uniqueness of Equations 24 3.4 Intersections with -

CATALAN's CURVE from a 1856 Paper by E. Catalan Part
CATALAN'S CURVE from a 1856 paper by E. Catalan Part - VI C. Masurel 13/04/2014 Abstract We use theorems on roulettes and Gregory's transformation to study Catalan's curve in the class C2(n; p) with angle V = π=2 − 2u and curves related to the circle and the catenary. Catalan's curve is defined in a 1856 paper of E. Catalan "Note sur la theorie des roulettes" and gives examples of couples of curves wheel and ground. 1 The class C2(n; p) and Catalan's curve The curves C2(n; p) shares many properties and the common angle V = π=2−2u (see part III). The polar parametric equations are: cos2n(u) ρ = θ = n tan(u) + 2:p:u cosn+p(2u) At the end of his 1856 paper Catalan looked for a curve such that rolling on a line the pole describe a circle tangent to the line. So by Steiner-Habich theorem this curve is the anti pedal of the wheel (see part I) associated to the circle when the base-line is the tangent. The equations of the wheel C2(1; −1) are : ρ = cos2(u) θ = tan(u) − 2:u then its anti-pedal (set p ! p + 1) is C2(1; 0) : cos2 u 1 ρ = θ = tan u −! ρ = cos 2u 1 − θ2 this is Catalan's curve (figure 1). 1 Figure 1: Catalan's curve : ρ = 1=(1 − θ2) 2 Curves such that the arc length s = ρ.θ with initial condition ρ = 1 when θ = 0 This relation implies by derivating : r dρ ds = ρdθ + dρθ = ρ2 + ( )2dθ dθ Squaring and simplifying give : 2ρθdθ dρ + (dρ)2θ2 = (dρ)2 So we have the evident solution dρ = 0 this the traditionnal circle : ρ = 1 But there is another one more exotic given by the other part of equation after we simplify by dρ 6= 0. -
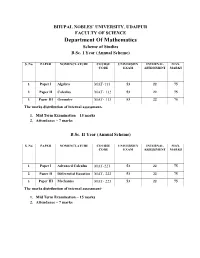
Department of Mathematics Scheme of Studies B.Sc
BHUPAL NOBLES` UNIVERSITY, UDAIPUR FACULTY OF SCIENCE Department Of Mathematics Scheme of Studies B.Sc. I Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Algebra MAT-111 53 22 75 2. Paper II Calculus MAT- 112 53 22 75 3. Paper III Geometry MAT- 113 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. II Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Advanced Calculus MAT-221 53 22 75 2. Paper II Differential Equation MAT- 222 53 22 75 3. Paper III Mechanics MAT- 223 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. III Year (Annual Scheme) S. PAPER NOMENCLATURE COURSE CODE UNIVERSITY INTERNAL MAX. No. EXAM ASSESSMENT MARKS 1. Paper I Real Analysis MAT-331 53 22 75 2. Paper II Advanced Algebra MAT- 332 53 22 75 3. Paper Numerical Analysis MAT-333 (A) 53 22 75 III Mathematical MAT-333 (B) Quantitative Techniques Mathematical MAT-333 (C) Statistics The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks BHUPAL NOBLES’ UNIVERSITY, UDAIPUR Department of Mathematics Syllabus 2017 -2018 (COMMON FOR THE FACULTIES OF ARTS & SCIENCE) B.A. / B. Sc. FIRST YEAR EXAMINATIONS 2017-2020 MATHEMATICS Theory Papers Name Papers Code Papers Maximum Papers hours/ Marks BA/ week B.Sc. Paper I ALGEBRA MAT-111 3 75 Paper II CALCULUS MAT-112 3 75 Paper III GEOMETRY MAT-113 3 75 Total Marks 225 NOTE: 1. -
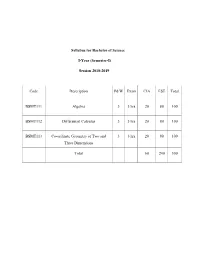
Syllabus for Bachelor of Science I-Year (Semester-I) Session 2018
Syllabus for Bachelor of Science I-Year (Semester-I) Session 2018-2019 Code Description Pd/W Exam CIA ESE Total BSMT111 Algebra 3 3 hrs 20 80 100 BSMT112 Differential Calculus 3 3 hrs 20 80 100 BSMT113 Co-ordinate Geometry of Two and 3 3 hrs 20 80 100 Three Dimensions Total 60 240 300 BSMT111: ALGEBRA Matrix: The characteristic equation of matrix: Eigen Values and Eigen Unit-I Vectors, Diagonalization of matrix, Cayley-Hamilton theorem(Statement 9 and proof),and its use in finding the inverse of a Matrix. Theory of equation: Relation between roots and coefficient of the equation Unit-II Symmetric function of roots. Solution of cubic equation by Cordon’s 9 method and Biquadratic equitation by Ferrari’s method. Infinite series: Convergent series, convergence of geometric series, And Unit-III necessary condition for the convergent series, comparison tests: Cauchy 9 root test. D’Alembert’s Ratio test, Logarithmic test, Raabe’s test, De’ Morgan and Unit-IV Bertrand’s test, Cauchy’s condensation test, Leibnitz’s test of alternative 9 series, Absolute convergent. Unit-V Inequalities and Continued fractions. 9 Suggested Readings: 1. Bhargav and Agarwal:Algebra, Jaipur publishing House, Jaipur. 2. Vashistha and Vashistha : Modern Algebra, Krishna Prakashan, Meerut. 3. Gokhroo, Saini and Tak: Algebra,Navkar prakashan, Ajmer.. 4. M-Ray and H. S. Sharma: A Text book of Higher Algebra, New Delhi, BSMT112: Differential Calculus Unit-I Polar Co-ordinates, Angle between radius vector and the tangents. Angle 9 between curves in polar form, length of polar subs tangent and subnormal, pedal equation of a curve, derivatives of an arc. -

Group B Higher Algebra & Trigonometry
UNIVERSITY DEPARTMENT OF MATHEMATICS, DSPMU, RANCHI CBCS PATTERN SYLLABUS Semester Mat/ Sem VC1- Analytical Geometry 2D, Trigonometry Instruction: Ten questions will be set. Candidates will be required to answer Seven Questions. Question no. 1 will be Compulsory consisting of 10 short answer type covering entire syllabus uniformly. Each question will be of 2 marks. Out of remaining 9 questions candidates will be required to answer 6 questions selecting at least one from each group. Each question will be of 10 marks. GROUP-A ANALYTICAL GEOMETRY OF TWO DIMENSIONS Change of rectangular axes. Condition for the general equation of second degree to represent parabola, ellipse, hyperbola and reduction into standard forms. Equations of tangent and normal (Using Calculus). Chord of contact, Pole and Polar. Pair of tangents in reference to general equation of conic. Axes, centre, director circle in reference to general equation of conic. Polar equation of conic. 5 Questions GROUP B HIGHER ALGEBRA & TRIGONOMETRY Statement and proof of binomial theorem for any index, exponential and logarithmic series. 1 Question De Moivre's theorem and its applications. Trigonometric and Exponential functions of complex argument and hyperbolic functions. Summation of Trigonometrical series. Factorisation of sin , cos 3 Questions Books Recommended: 1. Analytical Geometry& Vector Analysis - B. K. Kar, Books& Allied Co., Kolkata 2. Analytical Geometry of two dimension - Askwith 3. Coordinate Geometry- SL Loney. 4. Trigonometry- Das and Mukheriee 5. Trigonometry- Dasgupta UNIVERSITY DEPARTMENT OF MATHEMATICS, DSPMU, RANCHI CBCS PATTERN SYLLABUS Semester Mat/ Sem IVC 2- Differential Calculus and Vector Calculus Instruction: Ten questions will be set. Candidates will be required to answer Seven Questions. -

1 CHAPTER 2 CONIC SECTIONS 2.1 Introduction a Particle Moving Under the Influence of an Inverse Square Force Moves in an Orbit T
1 CHAPTER 2 CONIC SECTIONS 2.1 Introduction A particle moving under the influence of an inverse square force moves in an orbit that is a conic section; that is to say an ellipse, a parabola or a hyperbola. We shall prove this from dynamical principles in a later chapter. In this chapter we review the geometry of the conic sections. We start off, however, with a brief review (eight equation-packed pages) of the geometry of the straight line. 2.2 The Straight Line It might be thought that there is rather a limited amount that could be written about the geometry of a straight line. We can manage a few equations here, however, (there are 35 in this section on the Straight Line) and shall return for more on the subject in Chapter 4. Most readers will be familiar with the equation y = mx + c 2.2.1 for a straight line. The slope (or gradient) of the line, which is the tangent of the angle that it makes with the x-axis, is m, and the intercept on the y-axis is c. There are various other forms that may be of use, such as x y +=1 2.2.2 x00y yy− 1 yy21− = 2.2.3 xx− 1 xx21− which can also be written x y 1 x1 y1 1 = 0 2.2.4 x2 y2 1 x cos θ + y sin θ = p 2.2.5 2 The four forms are illustrated in figure II.1. y y slope = m y 0 c x x x0 2.2.1 2.2.2 y y • (x2 , y2 ) • ( x1 , y1 ) p x α x 2.2.3 or 4 2.2.5 FIGURE II.1 A straight line can also be written in the form Ax + By + C = 0. -

PHD THESIS ISOPTIC CURVES and SURFACES Csima Géza Supervisor
PHD THESIS ISOPTIC CURVES AND SURFACES Csima Géza Supervisor: Szirmai Jenő associate professor BUTE Mathematical Institute, Department of Geometry BUTE 2017 Contents 0.1 Introduction . V 1 Isoptic curves on the Euclidean plane 1 1.1 Isoptics of closed strictly convex curves . 1 1.1.1 Example . 3 1.2 Isoptic curves of Euclidean conic sections . 4 1.2.1 Ellipse . 5 1.2.2 Hyperbola . 7 1.2.3 Parabola . 10 1.3 Isoptic curves to finite point sets . 12 1.4 Inverse problem . 15 2 Isoptic surfaces in the Euclidean space 18 2.1 Isoptic hypersurfaces in En ........................ 18 2.1.1 Isoptic hypersurface of (n−1)−dimensional compact hypersur- faces in En ............................. 19 2.1.2 Isoptic surface of rectangles . 20 2.1.3 Isoptic surface of ellipsoids . 23 2.2 Isoptic surfaces of polyhedra . 25 2.2.1 Computations of the isoptic surface of a given regular tetrahedron 27 2.2.2 Some isoptic surfaces to Platonic and Archimedean polyhedra 29 3 Isoptic curves of conics in non-Euclidean constant curvature geome- tries 31 3.1 Projective model . 31 3.1.1 Example: Isoptic curve of the line segment on the hyperbolic and elliptic plane . 32 3.1.2 The general method . 33 3.2 Elliptic conics and their isoptics . 34 3.2.1 Equation of the elliptic ellipse and hyperbola . 34 3.2.2 Equation of the elliptic parabola . 36 II 3.2.3 Isoptic curves of elliptic ellipse and hyperbola . 36 3.2.4 Isoptic curves of elliptic parabola . 37 3.3 Hyperbolic conic sections and their isoptics . -

On the Pentadeltoid'
ON THE PENTADELTOID' BY R. P. STEPHENS Introductory. In his Orthocentric Properties of the Plane n-Line, Professor Morley| makes use of a curve of class 2n — 1, which he calls the A2"-1. Of these curves, the deltoid (n = 2) is the well-known three-cusped hypocycloid; but the curve of class five ( n. = 3 ), which I shall call Pentadeltoid, and more frequently represent by the symbol A'', is not so well known, though its shape and a few of its properties were known to Clifford $. I shall here prove some of the properties of the pentadeltoid. My purpose in presenting this curve is two- fold: 1. the discussion of a curve of many interesting properties; 2. the illus- tration of the use of vector analysis as a tool in the metric geometry of the plane. The line equation of a curve is here uniformly expressed by means of con- jugate coordinates,§ while the point equation is expressed by means of what is commonly called the map equation, that is, a point of the curve is expressed as a function of a parameter t, which is limited to the unit circle and is, therefore, always equal in absolute value to unity. Throughout I shall consider y and b as conjugates of x and a, respectively; that is, if X and Y are rectangular coordinates of a point, then x = X+iY, y = X-iY, and similarly for a and b.\\ Some of the properties of the curves of class 2« — 1 and of degree 2n, easily inferred from those of the A5, are also proved, but there has been no attempt at making a complete study of the general case. -

Geometrical Constructions 1) (See Geometrical Constructions 1)
GEOMETRICAL CONSTRUCTIONS 2 by Johanna PÉK PhD Budapest University of Technology and Economics Faculty of Architecture Department of Architectural Geometry and Informatics Table of contents • Radical line, radical center. Apollonius’ problem • Conic sections • Basic constructions on ellipses • Basic constructions on parabolas. Basic constructions on hyperbolas • Approximate constructions. Constructions of algebraic operations • Metric problems in space • Polyhedra. Regular polyhedra • Cone, cylinder, sphere • Multi-view representation • Axonometrical representation 2 Power of a point Power of a point (or circle power) The power of a point P with respect to a circle is defined by the product PA ∙ PB where AB is a secant passing through P. Remark: The point P can be an inner point of the circle. 2 Theorem: Using the notation of the figure, PA ∙ PB = PK ∙ PL = PT Sketch of the proof 3 RADICAL LINE, RADICAL CENTER – 1 Radical line (of two circles) is the locus of points of equal (circle) power with respect to two nonconcentric circles. This line is perpendicular to the line of centers. If two circles have common points K, L then their radical line is line KL. Alternative definition: radical line is the locus of points at which tangents drawn to both circles have the same length. (See point P.) lecture & practical 4 Radical line, radical center – 2 Radical center (of three circles): The radical lines of three circles intersect each other in a special pont called the radical center (or power center). lecture & practical 5 Radical line, radical center – 3 The radical line exists even if the two circles have no common points.