DOCSLIB.ORG

Studies of Subdwarf B Stars Michael David Reed Iowa State University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Studies of Subdwarf B Stars Michael David Reed Iowa State University Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2001 Studies of subdwarf B stars Michael David Reed Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Astrophysics and Astronomy Commons Recommended Citation Reed, Michael David, "Studies of subdwarf B stars " (2001). Retrospective Theses and Dissertations. 665. https://lib.dr.iastate.edu/rtd/665 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6" x 9" black and white photographic prints are available for any photographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. ProQuest Information and Learning 300 North Zeeb Road, Ann Arbor, Ml 48106-1346 USA 800-521-0600 Studies of Subdwarf B Stars by Michael David Reed A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Astrophysics Program of Study Committee: Steven D. Kawaler, Major Professor Scot J. Kleinman Russell J. Lavery Curt Struck Hal Stem Paul Can field Iowa State University Ames, Iowa 2001 Copyright © Michael David Reed, 2001. All rights reserved. UMI Number: 3034212 UMI ® UMI Microform 3034212 Copyright 2002 by ProQuest Information and Learning Company. All rights reserved. This microform edition is protected against unauthorized copying under Title 17, United States Code. ProQuest Information and Learning Company 300 North Zeeb Road P.O. Box 1346 Ann Arbor, Ml 48106-1346 ii Graduate College Iowa State University This is to certify that the doctoral dissertation of Michael David Reed has met the dissertation requirements of Iowa State University Signature was redacted for privacy. Major Professor Signature was redacted for privacy. For the Major Program iii TABLE OF CONTENTS ABSTRACT xvii CHAPTER 1. INTRODUCTION 1 1.1 Evolution of Solar-Type Stars 2 1.2 Subdwarf B Stars 3 1.2.1 Outside Appearances 5 1.2.2 Binarity 6 1.2.3 Speculation About the Origins of Subdwarf B Stars 9 1.3 Pulsating Subdwarf B Stars 10 1.3.1 Overview of Pulsation Properties 11 1.3.2 Pulsating Subdwarf B Stars as Probes of Stellar Evolution and Stellar Systems 11 1.4 The Goals of this Work 12 CHAPTER 2. ASTEROSEISMOLOGY METHODS AND TOOLS 15 2.1 Obtaining and Reducing Time-Series Photometry 16 2.1.1 Photoelectric Photometry 16 2.1.2 Data Reduction 17 2.1.3 The Temporal Spectrum 18 2.1.4 Beating Down Aliases with Multi Site Data 19 2.2 Pulsation Theory 22 2.2.1 Classes of Pulsation Modes 23 2.2.2 Asymptotic Properties of Nonradial Modes 25 2.2.3 Effects of Rotation on Pulsation Frequencies 27 IV 2.2.4 Mode Trapping 28 2.2.5 Changes in the Pulsation Period 28 2.3 Detailed Stellar Models 29 2.3.1 Evolutionary Models 29 2.3.2 Pulsation Period Calculation 31 2.4 Practical Implications of Pulsation Theory 32 2.4.1 Observable i Values 32 2.4.2 Pattern Matching 32 2.4.3 Abundance of Pulsations 33 2.4.4 Measuring Evolutionary Changes 34 2.5 Successful Applications of Asteroseismology 35 2.5.1 A Single, Rich Pulsater 35 2.5.2 A Single Star, Viewed Over Several Seasons 36 2.5.3 Using an Ensemble of Pulsators to Identify Pulsation Modes 36 2.5.4 O-C 38 2.6 Conclusions 40 CHAPTER 3. SUBDWARF B STARS AS BINARIES 41 3.1 Observed Subdwarf B Stars in Binaries 41 3.1.1 Methods of Detecting Binary Stars 41 3.1.2 Binary Frequency of Subdwarf B Stars 42 3.1.3 Theoretical Considerations 44 3.2 Effects on Pulsation Due to Binarity 45 3.2.1 Time Delay and Doppler Shift 45 3.2.2 O-C 48 3.2.3 Complicated Light Curves 48 3.2.4 Temporal Spectra of Simulated Data 51 3.2.5 Reducing Data with Orbital Aliasing 55 3.2.6 Correcting the Lightcurve for Binarity 60 V 3.3 Other Possible Manifestations of Binarity 63 3.4 Conclusions 63 CHAPTER 4. BACKGROUND AND OBSERVATIONS OF INDIVID­ UAL STARS 65 4.1 PB 8783 65 4.2 PG 1605+072 68 4.3 Feige 48 73 4.4 PG 1336-018 78 4.4.1 Xcov 17 Observations 80 4.4.2 Xcov 21 Observations 81 4.5 Conclusion 84 CHAPTER 5. PATTERN ANALYSIS 92 5.1 PB8783 93 5.1.1 Complications Due to Binarity 94 5.2 PG1605 97 5.3 Feige 48 98 5.4 PG1336 100 5.4.1 Xcov 17 101 5.4.2 Xcov 21 101 5.5 Conclusion 102 CHAPTER 6. STABILITY AND EVOLUTION OF PULSATIONS 105 6.1 PB8783 106 6.2 PG1605 109 6.3 Feige 48 114 6.4 PG1336 117 6.5 Conclusions 118 CHAPTER 7. STUDIES OF THE ENTIRE GROUP 120 7.1 The Pulsation Dependence Across the HR Diagram 120 vi 7.2 Scaling with Surface Gravity and Radius 121 7.3 Conclusions 125 CHAPTER 8. NEW TOOLS FOR ASTEROSEISMOLOGY 126 8.1 Using Eclipses to Identify Pulsation Modes 126 8.1.1 Eclipse modeling 126 8.1.2 Eclipse Data 128 8.2 Tipped pulsation axis 132 8.2.1 Determining the Mode Structure in Xcov Data- Simulations 133 8.2.2 Xcov 21 Data 139 8.3 Tipped eclipses 140 8.4 Results 141 CHAPTER 9. CONCLUSIONS 145 9.1 Results from this Work 145 9.1.1 Observations 145 9.1.2 Applying the Tools of Asteroseismology 146 9.1.3 Developing New Tools 150 9.2 Ramifications of this Work 152 9.3 Where to go for answers 154 9.4 Conclusion 155 APPENDIX A. SEARCHING FOR COMPANIONS TO SUBDWARF B STARS USING INFRARED COLORS 156 BIBLIOGRAPHY 168 vii LIST OF TABLES Table 3.1 Orbital parameters for simulated light curves 53 Table 3.2 Grouping of data used in simulations 53 Table 3.3 Effects of binarity on pulsation for binaries of various lengths 62 Table 4.1 Properties of the four sdBV stars selected for study in this work; in order of increase log g 66 Table 4.2 The 11 modes detected during the multi-site campaign. (From O'Donoghue et al., 1998) for PB 8783 68 Table 4.3 The 10 largest amplitude modes of PG 1605 detected during the multi- site campaign. (From Kilkenny et al. 1999) 73 Table 4.4 Observations of PG 1605 74 Table 4.5 Observations of Feige 48 76 Table 4.6 Subgroups used in pulsation analysis for Feige 48 77 Table 4.7 Comparison of frequencies (in /^Hz) detected in various runs for Feige 48. Formal LSQ errors are provided in parentheses 78 Table 4.8 Best solution using all the data for Feige 48. Formal LSQ errors in parenthesis 78 Table 4.9 Period list for PG 1336 from Xcov 17 (Formal LSQ errors are in paren­ theses) 87 Table 4.10 Observations of PG 1336 from Xcov 21 88 Table 4.11 Period List for PG 1336 from Xcov 21. Formal LSQ errors in parenthesis.(/ denote modes also detected in Xcov 17 data, g denotes modes observed only in Xcov 21.) 90 viii Table 5.1 Separations of the 11 modes in Table 4.2 for PB 8783 94 Table 5.2 Comparison between Model and Observed modes in PG 1605. (From Kawaler, 1999) 97 Table 5.3 Comparison of observed pulsation periods with best-fit evolutionary model of appropriate Teff and log g for Feige 48 99 Table 5.4 Comparison of observed stellar parameters with models for Feige 48. 100 Table 5.5 Comparison of Model to Observations in PG 1336 101 Table 5.6 Observed periods (from Xcov21) of PG 1336 split by an integer number of rotation frequencies 102 Table 6.1 Groupings used for phase calculations of PG 1605. Note that the mul- tisite data contains subgroups used in Figure 6.4 113 Table 6.2 Least squares determined frequencies, in fj.Hz, near 2742/iHz by year for PG 1605. Amplitudes (in mma) are in parenthesis 113 Table 8.1 Pulsation modes detected in simulations 127 Table 8.2 Period List for PG 1336 from Xcov 21 for primary eclipse data. (Formal LSQ errors in parenthesis.) 131 Table 8.3 Phases and FT signatures for individual pulsation modes in the case of a tipped pulsation axis 136 Table 8.4 Phases for pulsations in simulated 'A' and 'B' data sets.
Load more

Recommended publications
  • White Dwarfs
    Chandra X-Ray Observatory X-Ray Astronomy Field Guide White Dwarfs White dwarfs are among the dimmest stars in the universe. Even so, they have commanded the attention of astronomers ever since the first white dwarf was observed by optical telescopes in the middle of the 19th century. One reason for this interest is that white dwarfs represent an intriguing state of matter; another reason is that most stars, including our sun, will become white dwarfs when they reach their final, burnt-out collapsed state. A star experiences an energy crisis and its core collapses when the star's basic, non-renewable energy source - hydrogen - is used up. A shell of hydrogen on the edge of the collapsed core will be compressed and heated. The nuclear fusion of the hydrogen in the shell will produce a new surge of power that will cause the outer layers of the star to expand until it has a diameter a hundred times its present value. This is called the "red giant" phase of a star's existence. A hundred million years after the red giant phase all of the star's available energy resources will be used up. The exhausted red giant will puff off its outer layer leaving behind a hot core. This hot core is called a Wolf-Rayet type star after the astronomers who first identified these objects. This star has a surface temperature of about 50,000 degrees Celsius and is A composite furiously boiling off its outer layers in a "fast" wind traveling 6 million image of the kilometers per hour.
    [Show full text]
  • Meet the Family
    Open Astronomy 2014; 1 Research Article Open Access Stephan Geier*, Roy H. Østensen, Peter Nemeth, Ulrich Heber, Nicola P. Gentile Fusillo, Boris T. Gänsicke, John H. Telting, Elizabeth M. Green, and Johannes Schaffenroth Meet the family − the catalog of known hot subdwarf stars DOI: DOI Received ..; revised ..; accepted .. Abstract: In preparation for the upcoming all-sky data releases of the Gaia mission, we compiled a catalog of known hot subdwarf stars and candidates drawn from the literature and yet unpublished databases. The catalog contains 5613 unique sources and provides multi-band photometry from the ultraviolet to the far infrared, ground based proper motions, classifications based on spectroscopy and colors, published atmospheric parameters, radial velocities and light curve variability information. Using several different techniques, we removed outliers and misclassified objects. By matching this catalog with astrometric and photometric data from the Gaia mission, we will develop selection criteria to construct a homogeneous, magnitude-limited all-sky catalog of hot subdwarf stars based on Gaia data. As first application of the catalog data, we present the quantitative spectral analysis of 280 sdB and sdOB stars from the Sloan Digital Sky Survey Data Release 7. Combining our derived parameters with state-of-the-art proper motions, we performed a full kinematic analysis of our sample. This allowed us to separate the first significantly large sample of 78 sdBs and sdOBs belonging to the Galactic halo. Comparing the properties of hot subdwarfs from the disk and the halo with hot subdwarf samples from the globular clusters ω Cen and NGC2808, we found the fraction of intermediate He-sdOBs in the field halo population to be significantly smaller than in the globular clusters.
    [Show full text]
  • X-Ray Sun SDO 4500 Angstroms: Photosphere
    ASTR 8030/3600 Stellar Astrophysics X-ray Sun SDO 4500 Angstroms: photosphere T~5000K SDO 1600 Angstroms: upper photosphere T~5x104K SDO 304 Angstroms: chromosphere T~105K SDO 171 Angstroms: quiet corona T~6x105K SDO 211 Angstroms: active corona T~2x106K SDO 94 Angstroms: flaring regions T~6x106K SDO: dark plasma (3/27/2012) SDO: solar flare (4/16/2012) SDO: coronal mass ejection (7/2/2012) Aims of the course • Introduce the equations needed to model the internal structure of stars. • Overview of how basic stellar properties are observationally measured. • Study the microphysics relevant for stars: the equation of state, the opacity, nuclear reactions. • Examine the properties of simple models for stars and consider how real models are computed. • Survey (mostly qualitatively) how stars evolve, and the endpoints of stellar evolution. Stars are relatively simple physical systems Sound speed in the sun Problem of Stellar Structure We want to determine the structure (density, temperature, energy output, pressure as a function of radius) of an isolated mass M of gas with a given composition (e.g., H, He, etc.) Known: r Unknown: Mass Density + Temperature Composition Energy Pressure Simplifying assumptions 1. No rotation à spherical symmetry ✔ For sun: rotation period at surface ~ 1 month orbital period at surface ~ few hours 2. No magnetic fields ✔ For sun: magnetic field ~ 5G, ~ 1KG in sunspots equipartition field ~ 100 MG Some neutron stars have a large fraction of their energy in B fields 3. Static ✔ For sun: convection, but no large scale variability Not valid for forming stars, pulsating stars and dying stars. 4.
    [Show full text]
  • A Search for Radio Pulsations from Neutron Star Companions of Four
    Astronomy & Astrophysics manuscript no. 16098˙arxiv c ESO 2018 November 15, 2018 A search for radio pulsations from neutron star companions of four subdwarf B stars Thijs Coenen1, Joeri van Leeuwen2,1, and Ingrid H. Stairs3 1 Astronomical Institute ”Anton Pannekoek,” University of Amsterdam, P.O. Box 94249, 1090 GE, Amsterdam, The Netherlands 2 Stichting ASTRON, PO Box 2, 7990 AA Dwingeloo, The Netherlands 3 Dept. of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, B.C., V6T 1Z1 Canada ABSTRACT We searched for radio pulsations from the potential neutron star binary companions to subdwarf B stars HE 0532-4503, HE 0929- 0424, TON S 183 and PG 1232-136. Optical spectroscopy of these subdwarfs has indicated they orbit a companion in the neutron star mass range. These companions are thought to play an important role in the poorly understood formation of subdwarf B stars. Using the Green Bank Telescope we searched down to mean flux densities as low as 0.2 mJy, but no pulsed emission was found. We discuss the implications for each system. 1. Introduction Several such binary formation channels have been hypoth- esized. For an sdB to form, a light star must lose most of its The study of millisecond pulsars (MSPs) enables several types hydrogen envelope and ignite helium in its core. In these binary of research in astrophysics, ranging from binary evolution (e.g. systems, sdB stars can be formed through phases of Common Edwards & Bailes, 2001), to the potential detection of back- Envelope evolution where the envelope is ejected, or through ground gravitational radiation using a large set of pulsars with stable Roche Lobe overflow stripping the donor star of its hydro- stable timing properties (Jaffe & Backer, 2003).
    [Show full text]
  • The X-Ray Universe 2017 List of Posters
    The X-ray Universe 2017 List of Posters A - Solar System, Exoplanets and Star-Planet-Interaction A01 Frederic Marin Transmitted and polarized scattered fluxes by the exoplanet HD 189733b in X-rays B - Star formation, Young Stellar Objects, Cool and Hot Stars B01 Yael Naze A legacy survey of early B-type stars using the RGS B02 Stefan Czesla The coronae of Kepler superflare stars B03 Mauricio Elías Chávez ESTIMATION OF THE STAR FORMATION RATE (SFR) THROUGH DATA ANALYSIS OF SWIFT'S LONG- GRBs FROM 2008 TO 2017 B04 Federico Fraschetti Local protoplanetary disk ionisation by T Tauri star energetic particles B05 Martin A. Guerrero The XMM-Newton View of Wolf-Rayet Bubbles B06 Sandro Mereghetti X-rays as a new tool to study the winds of hot subdwarf stars B07 Yael Naze Zeta Pup variability revisited B08 John Pye A survey of long-term X-ray variability in cool stars B09 Gregor Rauw The flaring activity of pre-main sequence stars in NGC6530 B10 Beate Stelzer Activity and rotation of the X-ray emitting Kepler stars B11 Beate Stelzer Calibrating the time-evolution of the X-ray emission of M dwarfs C - White Dwarfs, Cataclysmic Variables and Novae C01 Andrej Dobrotka XMM-Newton observation of nova like system MV Lyr and search for source of the fast variability detected in Kepler data C02 Cigdem Gamsizkan Reanalysis of high-resolution XMM-Newton data of V2491 Cygni using models of collisionally ionized hot absorbers C03 Isabel J. Lima Simultaneous modelling of X-ray emission and optical polarization of intermediate polars: the case of V405 Aur C04 Arti Joshi XMM-Newton observations of an asynchronously rotating polar CD Ind C05 Sandro Mereghetti The mysterious companion of the hot subdwarf HD 49798 C06 Nasrin Talebpour X-ray Spectra of the Cataclysmic Variable LS Peg using XMM-Newton and SWIFT data Sheshvan D - Isolated Neutron Stars & Magnetars D01 Jaziel G.
    [Show full text]
  • The Sun, Yellow Dwarf Star at the Heart of the Solar System NASA.Gov, Adapted by Newsela Staff
    Name: ______________________________ Period: ______ Date: _____________ Article of the Week Directions: Read the following article carefully and annotate. You need to include at least 1 annotation per paragraph. Be sure to include all of the following in your total annotations. Annotation = Marking the Text + A Note of Explanation 1. Great Idea or Point – Write why you think it is a good idea or point – ! 2. Confusing Point or Idea – Write a question to ask that might help you understand – ? 3. Unknown Word or Phrase – Circle the unknown word or phrase, then write what you think it might mean based on context clues or your word knowledge – 4. A Question You Have – Write a question you have about something in the text – ?? 5. Summary – In a few sentences, write a summary of the paragraph, section, or passage – # The sun, yellow dwarf star at the heart of the solar system NASA.gov, adapted by Newsela staff Picture and Caption ___________________________ ___________________________ ___________________________ Paragraph #1 ___________________________ ___________________________ This image shows an enormous eruption of solar material, called a coronal mass ejection, spreading out into space, captured by NASA's Solar Dynamics ___________________________ Observatory on January 8, 2002. Paragraph #2 Para #1 The sun is a hot ball made of glowing gases and is a type ___________________________ of star known as a yellow dwarf. It is at the heart of our solar system. ___________________________ Para #2 The solar system consists of everything that orbits the ___________________________ sun. The sun's gravity holds the solar system together, by keeping everything from planets to bits of dust in its orbit.
    [Show full text]
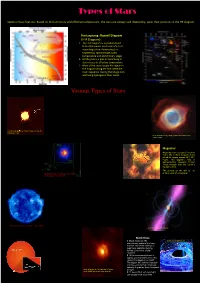
  • Brown Dwarf: White Dwarf: Hertzsprung -Russell Diagram (H-R
    Types of Stars Spectral Classifications: Based on the luminosity and effective temperature , the stars are categorized depending upon their positions in the HR diagram. Hertzsprung -Russell Diagram (H-R Diagram) : 1. The H-R Diagram is a graphical tool that astronomers use to classify stars according to their luminosity (i.e. brightness), spectral type, color, temperature and evolutionary stage. 2. HR diagram is a plot of luminosity of stars versus its effective temperature. 3. Most of the stars occupy the region in the diagram along the line called the main sequence. During that stage stars are fusing hydrogen in their cores. Various Types of Stars Brown Dwarf: White Dwarf: Brown dwarfs are sub-stellar objects After a star like the sun exhausts its nuclear that are not massive enough to sustain fuel, it loses its outer layer as a "planetary nuclear fusion processes. nebula" and leaves behind the remnant "white Since, comparatively they are very cold dwarf" core. objects, it is difficult to detect them. Stars with initial masses Now there are ongoing efforts to study M < 8Msun will end as white dwarfs. them in infrared wavelengths. A typical white dwarf is about the size of the This picture shows a brown dwarf around Earth. a star HD3651 located 36Ly away in It is very dense and hot. A spoonful of white constellation of Pisces. dwarf material on Earth would weigh as much as First directly detected Brown Dwarf HD 3651B. few tons. Image by: ESO The image is of Helix nebula towards constellation of Aquarius hosts a White Dwarf Helix Nebula 6500Ly away.
    [Show full text]
  • Stars IV Stellar Evolution Attendance Quiz
    Stars IV Stellar Evolution Attendance Quiz Are you here today? Here! (a) yes (b) no (c) my views are evolving on the subject Today’s Topics Stellar Evolution • An alien visits Earth for a day • A star’s mass controls its fate • Low-mass stellar evolution (M < 2 M) • Intermediate and high-mass stellar evolution (2 M < M < 8 M; M > 8 M) • Novae, Type I Supernovae, Type II Supernovae An Alien Visits for a Day • Suppose an alien visited the Earth for a day • What would it make of humans? • It might think that there were 4 separate species • A small creature that makes a lot of noise and leaks liquids • A somewhat larger, very energetic creature • A large, slow-witted creature • A smaller, wrinkled creature • Or, it might decide that there is one species and that these different creatures form an evolutionary sequence (baby, child, adult, old person) Stellar Evolution • Astronomers study stars in much the same way • Stars come in many varieties, and change over times much longer than a human lifetime (with some spectacular exceptions!) • How do we know they evolve? • We study stellar properties, and use our knowledge of physics to construct models and draw conclusions about stars that lead to an evolutionary sequence • As with stellar structure, the mass of a star determines its evolution and eventual fate A Star’s Mass Determines its Fate • How does mass control a star’s evolution and fate? • A main sequence star with higher mass has • Higher central pressure • Higher fusion rate • Higher luminosity • Shorter main sequence lifetime • Larger
    [Show full text]
  • Stellar Structure and Evolution
    Lecture Notes on Stellar Structure and Evolution Jørgen Christensen-Dalsgaard Institut for Fysik og Astronomi, Aarhus Universitet Sixth Edition Fourth Printing March 2008 ii Preface The present notes grew out of an introductory course in stellar evolution which I have given for several years to third-year undergraduate students in physics at the University of Aarhus. The goal of the course and the notes is to show how many aspects of stellar evolution can be understood relatively simply in terms of basic physics. Apart from the intrinsic interest of the topic, the value of such a course is that it provides an illustration (within the syllabus in Aarhus, almost the first illustration) of the application of physics to “the real world” outside the laboratory. I am grateful to the students who have followed the course over the years, and to my colleague J. Madsen who has taken part in giving it, for their comments and advice; indeed, their insistent urging that I replace by a more coherent set of notes the textbook, supplemented by extensive commentary and additional notes, which was originally used in the course, is directly responsible for the existence of these notes. Additional input was provided by the students who suffered through the first edition of the notes in the Autumn of 1990. I hope that this will be a continuing process; further comments, corrections and suggestions for improvements are most welcome. I thank N. Grevesse for providing the data in Figure 14.1, and P. E. Nissen for helpful suggestions for other figures, as well as for reading and commenting on an early version of the manuscript.
    [Show full text]
  • Supernovae Sparked by Dark Matter in White Dwarfs
    Supernovae Sparked By Dark Matter in White Dwarfs Javier F. Acevedog and Joseph Bramanteg;y gThe Arthur B. McDonald Canadian Astroparticle Physics Research Institute, Department of Physics, Engineering Physics, and Astronomy, Queen's University, Kingston, Ontario, K7L 2S8, Canada yPerimeter Institute for Theoretical Physics, Waterloo, Ontario, N2L 2Y5, Canada November 27, 2019 Abstract It was recently demonstrated that asymmetric dark matter can ignite supernovae by collecting and collapsing inside lone sub-Chandrasekhar mass white dwarfs, and that this may be the cause of Type Ia supernovae. A ball of asymmetric dark matter accumulated inside a white dwarf and collapsing under its own weight, sheds enough gravitational potential energy through scattering with nuclei, to spark the fusion reactions that precede a Type Ia supernova explosion. In this article we elaborate on this mechanism and use it to place new bounds on interactions between nucleons 6 16 and asymmetric dark matter for masses mX = 10 − 10 GeV. Interestingly, we find that for dark matter more massive than 1011 GeV, Type Ia supernova ignition can proceed through the Hawking evaporation of a small black hole formed by the collapsed dark matter. We also identify how a cold white dwarf's Coulomb crystal structure substantially suppresses dark matter-nuclear scattering at low momentum transfers, which is crucial for calculating the time it takes dark matter to form a black hole. Higgs and vector portal dark matter models that ignite Type Ia supernovae are explored. arXiv:1904.11993v3 [hep-ph] 26 Nov 2019 Contents 1 Introduction 2 2 Dark matter capture, thermalization and collapse in white dwarfs 4 2.1 Dark matter capture .
    [Show full text]
  • Detection and Characterization of Hot Subdwarf Companions of Massive Stars Luqian Wang
    Georgia State University ScholarWorks @ Georgia State University Physics and Astronomy Dissertations Department of Physics and Astronomy 8-13-2019 Detection And Characterization Of Hot Subdwarf Companions Of Massive Stars Luqian Wang Follow this and additional works at: https://scholarworks.gsu.edu/phy_astr_diss Recommended Citation Wang, Luqian, "Detection And Characterization Of Hot Subdwarf Companions Of Massive Stars." Dissertation, Georgia State University, 2019. https://scholarworks.gsu.edu/phy_astr_diss/119 This Dissertation is brought to you for free and open access by the Department of Physics and Astronomy at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Physics and Astronomy Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. DETECTION AND CHARACTERIZATION OF HOT SUBDWARF COMPANIONS OF MASSIVE STARS by LUQIAN WANG Under the Direction of Douglas R. Gies, PhD ABSTRACT Massive stars are born in close binaries, and in the course of their evolution, the initially more massive star will grow and begin to transfer mass and angular momentum to the gainer star. The mass donor star will be stripped of its outer envelope, and it will end up as a faint, hot subdwarf star. Here I present a search for the subdwarf stars in Be binary systems using the International Ultraviolet Explorer. Through spectroscopic analysis, I detected the subdwarf star in HR 2142 and 60 Cyg. Further analysis led to the discovery of an additional 12 Be and subdwarf candidate systems. I also investigated the EL CVn binary system, which is the prototype of class of eclipsing binaries that consist of an A- or F-type main sequence star and a low mass subdwarf.
    [Show full text]
  • Chapter 16 the Sun and Stars
    Chapter 16 The Sun and Stars Stargazing is an awe-inspiring way to enjoy the night sky, but humans can learn only so much about stars from our position on Earth. The Hubble Space Telescope is a school-bus-size telescope that orbits Earth every 97 minutes at an altitude of 353 miles and a speed of about 17,500 miles per hour. The Hubble Space Telescope (HST) transmits images and data from space to computers on Earth. In fact, HST sends enough data back to Earth each week to fill 3,600 feet of books on a shelf. Scientists store the data on special disks. In January 2006, HST captured images of the Orion Nebula, a huge area where stars are being formed. HST’s detailed images revealed over 3,000 stars that were never seen before. Information from the Hubble will help scientists understand more about how stars form. In this chapter, you will learn all about the star of our solar system, the sun, and about the characteristics of other stars. 1. Why do stars shine? 2. What kinds of stars are there? 3. How are stars formed, and do any other stars have planets? 16.1 The Sun and the Stars What are stars? Where did they come from? How long do they last? During most of the star - an enormous hot ball of gas day, we see only one star, the sun, which is 150 million kilometers away. On a clear held together by gravity which night, about 6,000 stars can be seen without a telescope.
    [Show full text]