DOCSLIB.ORG

Week 6: Topology & Real Analysis Notes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Week 6: Topology & Real Analysis Notes Christian Parkinson GRE Prep: Topology & Real Analysis Notes 1 Week 6: Topology & Real Analysis Notes To this point, we have covered Calculus I, Calculus II, Calculus III, Differential Equations, Linear Algebra, Complex Analysis and Abstract Algebra. These topics probably comprise more than 90% of the GRE math subject exam. The remainder of the exam is comprised of a seemingly random selection of problems from a variety of different fields (topology, real analysis, probability, combinatorics, discrete math, graph theory, algorithms, etc.). We can't hope to cover all of this, but we will state some relevant definitions and theorems in Topology and Real Analysis. Topology The field of topology is concerned with the shape of spaces and their behavior under continuous transformations. Properties regarding shape and continuity are phrased using the concept of open sets. Definition 1 (Topology / Open Sets). Let X be a set and τ be a collection of subsets of X. We say that τ is a topology on X if the following three properties hold: (i) ?;X 2 τ n \ (ii) If T1;:::Tn is a finite collection of members of τ, then Ti 2 τ i=1 [ (iii) If fTigi2I is any collection of members of τ, then Ti 2 τ i2I In this case, we call the pair (X; τ) a topological space and we call the sets T 2 τ open sets. Note, there are two topologies which we can always place on any set X: the trivial topol- ogy τ = f?;Xg and the discrete topology τ = P(X). Having defined open sets, we are able to define closed sets. Definition 2 (Closed Sets). Let (X; τ) be a topological space. A set S ⊂ X is called closed iff Sc 2 τ. That is, S is defined to be closed if Sc is open. The words open and closed can be a bit confusing here. Often times students mistak- enly assume that a set is either open or closed; that these terms are mutually exclusive and describe all sets. This is not the case. Indeed, sets can be open, closed, neither open nor closed, or both open and closed. In any topological space (X; τ), the sets ? and X are both open and closed. By De Morgan's laws, since finite intersections and arbitrary unions of open sets are open, we see that finite unions and arbitrary intersections of closed sets remain closed. Example 3. The set of real numbers R becomes a topological space with open sets defined as follows. Define ? to be open and define ? 6= T ⊂ R to be open iff for all x 2 T , there Christian Parkinson GRE Prep: Topology & Real Analysis Notes 2 exists " > 0 such that (x − "; x + ") ⊂ T . Prototypical open sets in this topology are the open intervals (a; b) = fx 2 R : a < x < bg. Indeed, this interval is open because for x 2 (a; b), we can take " = minfjx − aj ; jx − bjg and we will find that (x − "; x + ") ⊂ (a; b). We can combine open sets via unions or (finite) intersections to make more open sets; for example (0; 1) [ (3; 5) is also an open set. Likewise, prototypical closed sets are closed in- tervals [a; b] = fx 2 R : a ≤ x ≤ bg, and any intersection or (finite) union of such sets will remain closed. As was observed above ? and R are both open and closed; in fact, in this space, these are the only sets which are both open and closed, though it is easy to construct sets which are neither open nor closed. Consider the set [0; 1) = fx 2 R : 0 ≤ x < 1g. This set is not open because the point 0 is in the set, but it cannot be surrounded by an interval which remains in the set. The complement of this set is (−∞; 0) [ [1; 1). This set is not open since 1 is in the set but cannot be surrounded by an interval which remains in the set. Since the complement is not open, the set [0; 1) is not closed. Note, this topology is called the standard topology on R. Example 4. While the above example defines the standard topology on R, it is easy to come up with non-standard topologies as well. Indeed, let us now define T ⊂ R to be open if T can be written as a union of sets of the form [a; b) = fx 2 R : a ≤ b < xg. These open sets comprise a topology on R. In this topology a prototypical open set is of the form [a; b). What other sets are open in this topology? Notice that 1 [ (a; b) = [a + 1=n; b) n=1 which shows that sets of the form (a; b) remain open in this topology. Also notice that since [a; b) is open, we define [a; b)c = (−∞; a) [ [b; 1) to be closed. However, both (−∞; a) and [b; 1) are easily seen to be open, so the set (−∞; a) [ [b; 1) is also open as a union of open sets. Since this set is open, it's complement [a; b) is closed. Hence in this topology, all sets of the form [a; b) are both open and closed. The intervals [a; b] are closed and not open in this topology. Note, this topology is called the lower limit topology on R. Notice in these example, the lower limit topology contains as open sets all of the sets which are open in the standard topology. In this way, the lower limit topology has \more" open sets and we can think of the lower limit topology \containing" the standard topology. We define these notions here. Definition 5 (Finer & Coarser Topologies). Suppose that X is a set and τ; σ are two topologies on X. If τ ⊂ σ, we say that τ is coarser than σ and that σ is finer than τ. On any space X, the finest topology is the discrete topology P(X) and the coarsest is the trivial topology f?;Xg. A finer topology is one that can more specifically distinguish between elements. Christian Parkinson GRE Prep: Topology & Real Analysis Notes 3 Definition 6 (Interior & Closure). Let (X; τ) be a topological space and let T ⊂ X. The interior of T is defined to be the largest open set contained in T . The closure of T is defined to be the smallest closed set containing T . We denote these by int(T ) and cl(T ) respectively. In symbols, we have [ \ int(T ) = S and cl(T ) = S: S2τ;S⊂T Sc2τ;T ⊂S Other common notations are T˚ for the interior of T , and T for the closure of T . Example 7. Considering R with the standard topology and a; b 2 R, a < b, we have int([a; b)) = (a; b) and cl([a; b)) = [a; b]. In both of the examples above, there was some notion of a \prototypical" open set, from which other open sets can be built. We give this notion a precise meaning here. Definition 8 (Basis (Base) for a Topology). Let X be a set and let β be a collection of subsets of X such that [ (1) X = B, B2β (2) if B1;B2 2 β, then for each x 2 B1 \ B2, there is B3 2 β such that x 2 B3 and B3 ⊂ B1 \ B2. Then the collection of sets τ = T : T = [i2I Bi for some collection of sets fBigi2I ⊂ β forms a topology on X. We call this τ the topology generated by β, and we call β a basis for the topology τ. This is half definition and half theorem: we are defining what it means to be a basis, and asserting that the topology generated by a basis is indeed a topology. If we can identify a basis for a topology, then the basis sets are the \prototypical" open sets, and all other open sets can be built as unions of the basis sets. Morally, basis sets are representatives for the open sets; if you can prove a given property for basis sets, the property will likely hold for all open sets. Often times it is easiest to define a topology by identifying a basis. Example 9. Above we defined the standard topology on R by saying that a set T is open if for all x 2 T , there is " > 0 such that (x − "; x + ") ⊂ T . It is important to see this definition of the topology; however, this is a much more analytic than topological definition. The topological way to define the standard topology on R would be to define it as the topol- ogy generated by the sets (a; b) where a; b 2 R, a < b. Indeed, these two definitions of the standard topology are equivalent as the following proposition shows. Christian Parkinson GRE Prep: Topology & Real Analysis Notes 4 Proposition 10. Suppose that (X; τ) is a topological space and that β is a basis for the topology τ. Then T 2 τ iff for all x 2 T , there is B 2 β such that x 2 B and B ⊂ T . It is important to identify when two bases in a topological space generate the same topol- ogy and this next proposition deals with that question. Proposition 11. Suppose that X is a set and β1, β2 are two bases for topologies τ1 and τ2. Then τ1 ⊂ τ2 iff for every B1 2 β1, and for every x 2 B1, there is B2 2 β2 such that x 2 B2 and B2 ⊂ B1. (Be very careful not to mix up the inclusions in this statement.
Load more

Recommended publications
  • Modes of Convergence in Probability Theory
    Modes of Convergence in Probability Theory David Mandel November 5, 2015 Below, fix a probability space (Ω; F;P ) on which all random variables fXng and X are defined. All random variables are assumed to take values in R. Propositions marked with \F" denote results that rely on our finite measure space. That is, those marked results may not hold on a non-finite measure space. Since we already know uniform convergence =) pointwise convergence this proof is omitted, but we include a proof that shows pointwise convergence =) almost sure convergence, and hence uniform convergence =) almost sure convergence. The hierarchy we will show is diagrammed in Fig. 1, where some famous theorems that demonstrate the type of convergence are in parentheses: (SLLN) = strong long of large numbers, (WLLN) = weak law of large numbers, (CLT) ^ = central limit theorem. In parameter estimation, θn is said to be a consistent ^ estimator or θ if θn ! θ in probability. For example, by the SLLN, X¯n ! µ a.s., and hence X¯n ! µ in probability. Therefore the sample mean is a consistent estimator of the population mean. Figure 1: Hierarchy of modes of convergence in probability. 1 1 Definitions of Convergence 1.1 Modes from Calculus Definition Xn ! X pointwise if 8! 2 Ω, 8 > 0, 9N 2 N such that 8n ≥ N, jXn(!) − X(!)j < . Definition Xn ! X uniformly if 8 > 0, 9N 2 N such that 8! 2 Ω and 8n ≥ N, jXn(!) − X(!)j < . 1.2 Modes Unique to Measure Theory Definition Xn ! X in probability if 8 > 0, 8δ > 0, 9N 2 N such that 8n ≥ N, P (jXn − Xj ≥ ) < δ: Or, Xn ! X in probability if 8 > 0, lim P (jXn − Xj ≥ 0) = 0: n!1 The explicit epsilon-delta definition of convergence in probability is useful for proving a.s.
    [Show full text]
  • 3. Closed Sets, Closures, and Density
    3. Closed sets, closures, and density 1 Motivation Up to this point, all we have done is define what topologies are, define a way of comparing two topologies, define a method for more easily specifying a topology (as a collection of sets generated by a basis), and investigated some simple properties of bases. At this point, we will start introducing some more interesting definitions and phenomena one might encounter in a topological space, starting with the notions of closed sets and closures. Thinking back to some of the motivational concepts from the first lecture, this section will start us on the road to exploring what it means for two sets to be \close" to one another, or what it means for a point to be \close" to a set. We will draw heavily on our intuition about n convergent sequences in R when discussing the basic definitions in this section, and so we begin by recalling that definition from calculus/analysis. 1 n Definition 1.1. A sequence fxngn=1 is said to converge to a point x 2 R if for every > 0 there is a number N 2 N such that xn 2 B(x) for all n > N. 1 Remark 1.2. It is common to refer to the portion of a sequence fxngn=1 after some index 1 N|that is, the sequence fxngn=N+1|as a tail of the sequence. In this language, one would phrase the above definition as \for every > 0 there is a tail of the sequence inside B(x)." n Given what we have established about the topological space Rusual and its standard basis of -balls, we can see that this is equivalent to saying that there is a tail of the sequence inside any open set containing x; this is because the collection of -balls forms a basis for the usual topology, and thus given any open set U containing x there is an such that x 2 B(x) ⊆ U.
    [Show full text]
  • Symmetric Rigidity for Circle Endomorphisms with Bounded Geometry
    SYMMETRIC RIGIDITY FOR CIRCLE ENDOMORPHISMS WITH BOUNDED GEOMETRY JOHN ADAMSKI, YUNCHUN HU, YUNPING JIANG, AND ZHE WANG Abstract. Let f and g be two circle endomorphisms of degree d ≥ 2 such that each has bounded geometry, preserves the Lebesgue measure, and fixes 1. Let h fixing 1 be the topological conjugacy from f to g. That is, h ◦ f = g ◦ h. We prove that h is a symmetric circle homeomorphism if and only if h = Id. Many other rigidity results in circle dynamics follow from this very general symmetric rigidity result. 1. Introduction A remarkable result in geometry is the so-called Mostow rigidity theorem. This result assures that two closed hyperbolic 3-manifolds are isometrically equivalent if they are homeomorphically equivalent [18]. A closed hyperbolic 3-manifold can be viewed as the quotient space of a Kleinian group acting on the open unit ball in the 3-Euclidean space. So a homeomorphic equivalence between two closed hyperbolic 3-manifolds can be lifted to a homeomorphism of the open unit ball preserving group actions. The homeomorphism can be extended to the boundary of the open unit ball as a boundary map. The boundary is the Riemann sphere and the boundary map is a quasi-conformal homeomorphism. A quasi-conformal homeomorphism of the Riemann 2010 Mathematics Subject Classification. Primary: 37E10, 37A05; Secondary: 30C62, 60G42. Key words and phrases. quasisymmetric circle homeomorphism, symmetric cir- arXiv:2101.06870v1 [math.DS] 18 Jan 2021 cle homeomorphism, circle endomorphism with bounded geometry preserving the Lebesgue measure, uniformly quasisymmetric circle endomorphism preserving the Lebesgue measure, martingales.
    [Show full text]
  • Arxiv:2102.05840V2 [Math.PR]
    SEQUENTIAL CONVERGENCE ON THE SPACE OF BOREL MEASURES LIANGANG MA Abstract We study equivalent descriptions of the vague, weak, setwise and total- variation (TV) convergence of sequences of Borel measures on metrizable and non-metrizable topological spaces in this work. On metrizable spaces, we give some equivalent conditions on the vague convergence of sequences of measures following Kallenberg, and some equivalent conditions on the TV convergence of sequences of measures following Feinberg-Kasyanov-Zgurovsky. There is usually some hierarchy structure on the equivalent descriptions of convergence in different modes, but not always. On non-metrizable spaces, we give examples to show that these conditions are seldom enough to guarantee any convergence of sequences of measures. There are some remarks on the attainability of the TV distance and more modes of sequential convergence at the end of the work. 1. Introduction Let X be a topological space with its Borel σ-algebra B. Consider the collection M˜ (X) of all the Borel measures on (X, B). When we consider the regularity of some mapping f : M˜ (X) → Y with Y being a topological space, some topology or even metric is necessary on the space M˜ (X) of Borel measures. Various notions of topology and metric grow out of arXiv:2102.05840v2 [math.PR] 28 Apr 2021 different situations on the space M˜ (X) in due course to deal with the corresponding concerns of regularity. In those topology and metric endowed on M˜ (X), it has been recognized that the vague, weak, setwise topology as well as the total-variation (TV) metric are highlighted notions on the topological and metric description of M˜ (X) in various circumstances, refer to [Kal, GR, Wul].
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Lecture 13: Basis for a Topology
    Lecture 13: Basis for a Topology 1 Basis for a Topology Lemma 1.1. Let (X; T) be a topological space. Suppose that C is a collection of open sets of X such that for each open set U of X and each x in U, there is an element C 2 C such that x 2 C ⊂ U. Then C is the basis for the topology of X. Proof. In order to show that C is a basis, need to show that C satisfies the two properties of basis. To show the first property, let x be an element of the open set X. Now, since X is open, then, by hypothesis there exists an element C of C such that x 2 C ⊂ X. Thus C satisfies the first property of basis. To show the second property of basis, let x 2 X and C1;C2 be open sets in C such that x 2 C1 and x 2 C2. This implies that C1 \ C2 is also an open set in C and x 2 C1 \ C2. Then, by hypothesis, there exists an open set C3 2 C such that x 2 C3 ⊂ C1 \ C2. Thus, C satisfies the second property of basis too and hence, is indeed a basis for the topology on X. On many occasions it is much easier to show results about a topological space by arguing in terms of its basis. For example, to determine whether one topology is finer than the other, it is easier to compare the two topologies in terms of their bases.
    [Show full text]
  • Advance Topics in Topology - Point-Set
    ADVANCE TOPICS IN TOPOLOGY - POINT-SET NOTES COMPILED BY KATO LA 19 January 2012 Background Intervals: pa; bq “ tx P R | a ă x ă bu ÓÓ , / / calc. notation set theory notation / / \Open" intervals / pa; 8q ./ / / p´8; bq / / / -/ ra; bs; ra; 8q: Closed pa; bs; ra; bq: Half-openzHalf-closed Open Sets: Includes all open intervals and union of open intervals. i.e., p0; 1q Y p3; 4q. Definition: A set A of real numbers is open if @ x P A; D an open interval contain- ing x which is a subset of A. Question: Is Q, the set of all rational numbers, an open set of R? 1 1 1 - No. Consider . No interval of the form ´ "; ` " is a subset of . We can 2 2 2 Q 2 ˆ ˙ ask a similar question in R . 2 Is R open in R ?- No, because any disk around any point in R will have points above and below that point of R. Date: Spring 2012. 1 2 NOTES COMPILED BY KATO LA Definition: A set is called closed if its complement is open. In R, p0; 1q is open and p´8; 0s Y r1; 8q is closed. R is open, thus Ø is closed. r0; 1q is not open or closed. In R, the set t0u is closed: its complement is p´8; 0q Y p0; 8q. In 2 R , is tp0; 0qu closed? - Yes. Chapter 2 - Topological Spaces & Continuous Functions Definition:A topology on a set X is a collection T of subsets of X satisfying: (1) Ø;X P T (2) The union of any number of sets in T is again, in the collection (3) The intersection of any finite number of sets in T , is again in T Alternative Definition: ¨ ¨ ¨ is a collection T of subsets of X such that Ø;X P T and T is closed under arbitrary unions and finite intersections.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • DEFINITIONS and THEOREMS in GENERAL TOPOLOGY 1. Basic
    DEFINITIONS AND THEOREMS IN GENERAL TOPOLOGY 1. Basic definitions. A topology on a set X is defined by a family O of subsets of X, the open sets of the topology, satisfying the axioms: (i) ; and X are in O; (ii) the intersection of finitely many sets in O is in O; (iii) arbitrary unions of sets in O are in O. Alternatively, a topology may be defined by the neighborhoods U(p) of an arbitrary point p 2 X, where p 2 U(p) and, in addition: (i) If U1;U2 are neighborhoods of p, there exists U3 neighborhood of p, such that U3 ⊂ U1 \ U2; (ii) If U is a neighborhood of p and q 2 U, there exists a neighborhood V of q so that V ⊂ U. A topology is Hausdorff if any distinct points p 6= q admit disjoint neigh- borhoods. This is almost always assumed. A set C ⊂ X is closed if its complement is open. The closure A¯ of a set A ⊂ X is the intersection of all closed sets containing X. A subset A ⊂ X is dense in X if A¯ = X. A point x 2 X is a cluster point of a subset A ⊂ X if any neighborhood of x contains a point of A distinct from x. If A0 denotes the set of cluster points, then A¯ = A [ A0: A map f : X ! Y of topological spaces is continuous at p 2 X if for any open neighborhood V ⊂ Y of f(p), there exists an open neighborhood U ⊂ X of p so that f(U) ⊂ V .
    [Show full text]
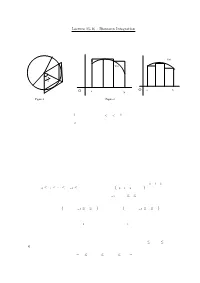
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Bounded Holomorphic Functions of Several Variables
    Bounded holomorphic functions of several variables Gunnar Berg Introduction A characteristic property of holomorphic functions, in one as well as in several variables, is that they are about as "rigid" as one can demand, without being iden- tically constant. An example of this rigidity is the fact that every holomorphic function element, or germ of a holomorphic function, has associated with it a unique domain, the maximal domain to which the function can be continued. Usually this domain is no longer in euclidean space (a "schlicht" domain), but lies over euclidean space as a many-sheeted Riemann domain. It is now natural to ask whether, given a domain, there is a holomorphic func- tion for which it is the domain of existence, and for domains in the complex plane this is always the case. This is a consequence of the Weierstrass product theorem (cf. [13] p. 15). In higher dimensions, however, the situation is different, and the domains of existence, usually called domains of holomorphy, form a proper sub- class of the class of aU domains, which can be characterised in various ways (holo- morphic convexity, pseudoconvexity etc.). To obtain a complete theory it is also in this case necessary to consider many-sheeted domains, since it may well happen that the maximal domain to which all functions in a given domain can be continued is no longer "schlicht". It is possible to go further than this, and ask for quantitative refinements of various kinds, such as: is every domain of holomorphy the domain of existence of a function which satisfies some given growth condition? Certain results in this direction have been obtained (cf.
    [Show full text]
  • Noncommutative Ergodic Theorems for Connected Amenable Groups 3
    NONCOMMUTATIVE ERGODIC THEOREMS FOR CONNECTED AMENABLE GROUPS MU SUN Abstract. This paper is devoted to the study of noncommutative ergodic theorems for con- nected amenable locally compact groups. For a dynamical system (M,τ,G,σ), where (M, τ) is a von Neumann algebra with a normal faithful finite trace and (G, σ) is a connected amenable locally compact group with a well defined representation on M, we try to find the largest non- commutative function spaces constructed from M on which the individual ergodic theorems hold. By using the Emerson-Greenleaf’s structure theorem, we transfer the key question to proving the ergodic theorems for Rd group actions. Splitting the Rd actions problem in two cases accord- ing to different multi-parameter convergence types—cube convergence and unrestricted conver- gence, we can give maximal ergodic inequalities on L1(M) and on noncommutative Orlicz space 2(d−1) L1 log L(M), each of which is deduced from the result already known in discrete case. Fi- 2(d−1) nally we give the individual ergodic theorems for G acting on L1(M) and on L1 log L(M), where the ergodic averages are taken along certain sequences of measurable subsets of G. 1. Introduction The study of ergodic theorems is an old branch of dynamical system theory which was started in 1931 by von Neumann and Birkhoff, having its origins in statistical mechanics. While new applications to mathematical physics continued to come in, the theory soon earned its own rights as an important chapter in functional analysis and probability. In the classical situation the sta- tionarity is described by a measure preserving transformation T , and one considers averages taken along a sequence f, f ◦ T, f ◦ T 2,..
    [Show full text]