DOCSLIB.ORG

Opportunities in Nuclear Science

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Opportunities in Nuclear Science OPPORTUNITIES IN NUCLEAR SCIENCE A Long-Range Plan for the Next Decade April 2002 The DOE/NSF Nuclear Science Advisory Committee U.S. Department of Energy • Office of Science • Division of Nuclear Physics National Science Foundation • Division of Physics • Nuclear Science Section This document was produced by the Berkeley Lab Technical and Electronic Information Department in collaboration with the Nuclear Science Advisory Committee. TEID JO#5547 This document was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, nor any of their contractors, subcontractors or their employees makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or any third party's use or the results of such use of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof or its contractors or subcontractors. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. OPPORTUNITIES IN NUCLEAR SCIENCE A Long-Range Plan for the Next Decade April 2002 The DOE/NSF Nuclear Science Advisory Committee U.S. Department of Energy • Office of Science • Division of Nuclear Physics National Science Foundation • Division of Physics • Nuclear Science Section The Nuclear Science Advisory Committee James Symons (Chair) Lawrence Berkeley National Laboratory Ricardo Alarcon Arizona State University Betsy Beise University of Maryland Tom Bowles Los Alamos National Laboratory Wit Busza Massachusetts Institute of Technology Jolie Cizewski Rutgers University Kees de Jager Jefferson Laboratory Alejandro Garcia University of Notre Dame Robert Janssens Argonne National Laboratory Krishna Kumar University of Massachusetts, Amherst Walter Loveland Oregon State University Larry McLerran Brookhaven National Laboratory Alice Mignerey University of Maryland Joel Moss Los Alamos National Laboratory Witold Nazarewicz University of Tennessee/Oak Ridge National Laboratory Shelley Page University of Manitoba Vijay Pandharipande University of Illinois Mark Riley Florida State University Richard Seto University of California, Riverside Brad Sherrill Michigan State University Edward Shuryak Stony Brook University Contents Executive Summary . 1 1. Overview and Recommendations . 3 2. The Science . 13 Protons and Neutrons: Structure and Interactions . 14 Atomic Nuclei: Structure and Stability . 28 QCD at High Energy Densities: Exploring the Nature of Hot Nuclear Matter . 43 Nuclear Astrophysics: The Origin of the Elements and the Evolution of Matter . 55 In Search of the New Standard Model . 70 3. Facilities for Nuclear Science . 85 4. The Nuclear Science Enterprise . 97 Education and Outreach . 98 Interdisciplinary Aspects . 107 International Collaborations and Cooperation . 111 Impact and Applications . 113 5. Looking to the Future . 121 6. Resources: Funding the 2002 Long-Range Plan . 137 Appendix . 142 Glossary of Facilities and Institutions . inside back cover Preface The DOE/NSF Nuclear Science Advisory Committee of the Department of Energy and the National Science Foundation is charged with providing advice on a continuing basis regarding the management of the national basic nuclear science research program. In July 2000, the Committee was asked to study the opportunities and priorities for U.S. nuclear physics research, and to develop a long-range plan that will serve as a frame- work for the coordinated advancement of the field for the next decade. The plan contained here is the fifth that has been pre- pared since the Committee was established. Each of the earlier plans has had substantial impact on new directions and initiatives in the field. NSAC is indebted to the Division of Nuclear Physics of the American Physical Society for organizing a series of four topical Town Meetings in late 2000 and early 2001. These meetings provided a forum for community input into the planning process and resulted in the production of White Papers that provide the scientific underpinning of this plan. A fifth White Paper on Education, covering the breadth of the field, was also written during this time. A Long-Range Plan Working Group (see Appendix) including the Committee members and additional representa- tives from the nuclear science community was formed to determine overall priorities for the field. The working group met in Santa Fe, NM during the week of March 25 , 2001. During this meeting, the scientific opportunities and priorities were discussed in depth and consensus was reached on the prioritized recommendations contained in this report. This report was prepared by the members of the Long- Range Plan Working Group. However, many others, too numerous to mention individually, contributed to the final document either as authors or readers. The chairman wishes to thank Douglas Vaughan, our technical editor, for his tireless efforts to create a coherent document. The Committee is indebted to all the members of our com- munity for their support of the planning process. Executive Summary Nuclear science is a key component of the nation’s This Plan has emerged from a process in which more research portfolio, providing fundamental insights into the than a thousand members of the nuclear science community nature of matter and nurturing applications critical to the participated by attending a series of public “town meet- nation’s health, security, and economic vitality. It is a field ings,” which led to the preparation of topical white papers. with tremendous breadth that has direct relevance to under- A smaller working group then prioritized the resulting rec- standing the evolution of matter in the universe. Nuclear ommendations. This Plan addresses the charge to NSAC to scientists today use sophisticated experimental and theoreti- develop a “framework for the coordinated advancement of cal tools to probe the properties of nuclei and nuclear matter the field.” The opportunities for such advancement are and of their ultimate constituents—quarks and gluons. At extraordinary, and addressing them will ensure the continu- the same time, nuclear science is probing key interdiscipli- ing vigor of nuclear science. The Plan includes the follow- nary questions: the basis of fundamental symmetries in ing four recommendations, which address critical funding nature, how matter emerged in the first moments of the uni- issues facing the present program and guide new invest- verse, the nature of supernovae, and the origin of elements ments for the future: in the cosmos. Nuclear science continues to have significant 1. Recent investments by the United States in new and impact on other fields. The field is also a prolific source of upgraded facilities have positioned the nation to con- today’s technological work force. More than half of nuclear tinue its world leadership role in nuclear science. The science Ph.D.’s apply their training outside their field— highest priority of the nuclear science community is to notably, in medicine, industry, and national defense. exploit the extraordinary opportunities for scientific The long-range plan for nuclear science that follows discoveries made possible by these investments. includes descriptions of recent progress across the full Increased funding for research and facility operations range of the field. One discovery, however, merits partic- is essential to realize these opportunities. ular attention. Remarkable new measurements show that Specifically, it is imperative to neutrinos produced by the nuclear reactions that power • Increase support for facility operations—especially the sun change their character on their 93-million-mile our unique new facilities, RHIC, CEBAF, and journey from the solar core to the Earth. This result is a NSCL—which will greatly enhance the impact of critical vindication of the theory of energy production in the nation’s nuclear science program. the sun: We now understand quantitatively what makes the sun shine. The transformation of neutrinos requires • Increase investment in university research and that they have mass, generating new questions at the same infrastructure, which will both enhance scientific time old ones are resolved. The Standard Model of ele- output and educate additional young scientists mentary particles provides no mechanism for neutrino vital to meeting national needs. mass and thus must be modified. In addition, theories of • Significantly increase funding for nuclear theory, the evolution of the universe and the nature of the missing which is essential for developing the full potential dark matter must take these discoveries into account. of the scientific program. EXECUTIVE SUMMARY 2. The Rare Isotope Accelerator (RIA) is our highest pri- 4. We strongly recommend the upgrade of CEBAF at ority for major new construction. RIA will be the Jefferson Laboratory to 12 GeV as soon as possible. world-leading facility for research in nuclear structure The 12-GeV upgrade of the unique CEBAF facility and nuclear astrophysics. is critical for our continued leadership in the experi- The exciting new scientific opportunities
Load more

Recommended publications
  • The Five Common Particles
    The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2.
    [Show full text]
  • Capture and Decay of Electroweak Wimponium
    Prepared for submission to JCAP MIT-CTP/4845 Capture and Decay of Electroweak WIMPonium Pouya Asadi,a Matthew Baumgart,a Patrick J. Fitzpatrick,b Emmett Krupczakb and Tracy R. Slatyerb aNew High Energy Theory Center, Rutgers University, Piscataway, NJ 08854 bCenter for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA E-mail: [email protected], [email protected], [email protected], fi[email protected], [email protected] Abstract. The spectrum of Weakly-Interacting-Massive-Particle (WIMP) dark matter gener- ically possesses bound states when the WIMP mass becomes sufficiently large relative to the mass of the electroweak gauge bosons. The presence of these bound states enhances the anni- hilation rate via resonances in the Sommerfeld enhancement, but they can also be produced directly with the emission of a low-energy photon. In this work we compute the rate for SU(2) triplet dark matter (the wino) to bind into WIMPonium – which is possible via single-photon emission for wino masses above 5 TeV for relative velocity v < O(10−2) – and study the subsequent decays of these bound states. We present results with applications beyond the wino case, e.g. for dark matter inhabiting a nonabelian dark sector; these include analytic capture and transition rates for general dark sectors in the limit of vanishing force carrier mass, efficient numerical routines for calculating positive and negative-energy eigenstates of a Hamiltonian containing interactions with both massive and massless force carriers, and a study of the scaling of bound state formation in the short-range Hulthén potential. In the arXiv:1610.07617v2 [hep-ph] 24 Jan 2017 specific case of the wino, we find that the rate for bound state formation is suppressed relative to direct annihilation, and so provides only a small correction to the overall annihilation rate.
    [Show full text]
  • Computing ATOMIC NUCLEI
    UNIVERSAL NUCLEAR ENERGY DENSITY FUNCTIONAL Computing ATOMIC NUCLEI Petascale computing helps disentangle the nuclear puzzle. The goal of the Universal Nuclear Energy Density Functional (UNEDF) collaboration is to provide a comprehensive description of all nuclei and their reactions based on the most accurate knowledge of the nuclear interaction, the most reliable theoretical approaches, and the massive use of computer power. Science of Nuclei the Hamiltonian matrix. Coupled cluster (CC) Nuclei comprise 99.9% of all baryonic matter in techniques, which were formulated by nuclear sci- the Universe and are the fuel that burns in stars. entists in the 1950s, are essential techniques in The rather complex nature of the nuclear forces chemistry today and have recently been resurgent among protons and neutrons generates a broad in nuclear structure. Quantum Monte Carlo tech- range and diversity in the nuclear phenomena that niques dominate studies of phase transitions in can be observed. As shown during the last decade, spin systems and nuclei. These methods are used developing a comprehensive description of all to understand both the nuclear and electronic nuclei and their reactions requires theoretical and equations of state in condensed systems, and they experimental investigations of rare isotopes with are used to investigate the excitation spectra in unusual neutron-to-proton ratios. These nuclei nuclei, atoms, and molecules. are labeled exotic, or rare, because they are not When applied to systems with many active par- typically found on Earth. They are difficult to pro- ticles, ab initio and configuration interaction duce experimentally because they usually have methods present computational challenges as the extremely short lifetimes.
    [Show full text]
  • B2.IV Nuclear and Particle Physics
    B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ......................
    [Show full text]
  • Nuclear Physics
    Nuclear Physics Overview One of the enduring mysteries of the universe is the nature of matter—what are its basic constituents and how do they interact to form the properties we observe? The largest contribution by far to the mass of the visible matter we are familiar with comes from protons and heavier nuclei. The mission of the Nuclear Physics (NP) program is to discover, explore, and understand all forms of nuclear matter. Although the fundamental particles that compose nuclear matter—quarks and gluons—are themselves relatively well understood, exactly how they interact and combine to form the different types of matter observed in the universe today and during its evolution remains largely unknown. Nuclear physicists seek to understand not just the familiar forms of matter we see around us, but also exotic forms such as those that existed in the first moments after the Big Bang and that exist today inside neutron stars, and to understand why matter takes on the specific forms now observed in nature. Nuclear physics addresses three broad, yet tightly interrelated, scientific thrusts: Quantum Chromodynamics (QCD); Nuclei and Nuclear Astrophysics; and Fundamental Symmetries: . QCD seeks to develop a complete understanding of how the fundamental particles that compose nuclear matter, the quarks and gluons, assemble themselves into composite nuclear particles such as protons and neutrons, how nuclear forces arise between these composite particles that lead to nuclei, and how novel forms of bulk, strongly interacting matter behave, such as the quark-gluon plasma that formed in the early universe. Nuclei and Nuclear Astrophysics seeks to understand how protons and neutrons combine to form atomic nuclei, including some now being observed for the first time, and how these nuclei have arisen during the 13.8 billion years since the birth of the cosmos.
    [Show full text]
  • The R-Process Nucleosynthesis and Related Challenges
    EPJ Web of Conferences 165, 01025 (2017) DOI: 10.1051/epjconf/201716501025 NPA8 2017 The r-process nucleosynthesis and related challenges Stephane Goriely1,, Andreas Bauswein2, Hans-Thomas Janka3, Oliver Just4, and Else Pllumbi3 1Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, 1050 Brussels, Belgium 2Heidelberger Institut fr¨ Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany 3Max-Planck-Institut für Astrophysik, Postfach 1317, 85741 Garching, Germany 4Astrophysical Big Bang Laboratory, RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan Abstract. The rapid neutron-capture process, or r-process, is known to be of fundamental importance for explaining the origin of approximately half of the A > 60 stable nuclei observed in nature. Recently, special attention has been paid to neutron star (NS) mergers following the confirmation by hydrodynamic simulations that a non-negligible amount of matter can be ejected and by nucleosynthesis calculations combined with the predicted astrophysical event rate that such a site can account for the majority of r-material in our Galaxy. We show here that the combined contribution of both the dynamical (prompt) ejecta expelled during binary NS or NS-black hole (BH) mergers and the neutrino and viscously driven outflows generated during the post-merger remnant evolution of relic BH-torus systems can lead to the production of r-process elements from mass number A > 90 up to actinides. The corresponding abundance distribution is found to reproduce the∼ solar distribution extremely well. It can also account for the elemental distributions observed in low-metallicity stars. However, major uncertainties still affect our under- standing of the composition of the ejected matter.
    [Show full text]
  • And Photon-Induced Processes at the LHC 1 Introduction
    Higgs and new physics in Pomeron- and photon-induced processes at the LHC David d'Enterria Laboratory for Nuclear Science, MIT, Cambridge, MA 02139-4307, USA ICC-UB & ICREA, Universitat de Barcelona, 08028 Barcelona, Catalonia 1 Introduction The primary goal of the CERN Large Hadron Collider (LHC) is the production of new particles predicted within or beyond the Standard Model (SM): Higgs boson, super- symmetric (SUSY) partners of the SM particles ... By colliding \head-on" protons at multi-TeV energies, one expects to produce new heavy particles in the under- lying high-pT parton-parton scatterings. Such collisions are characterised by large QCD activity and backgrounds which often complicate the identification of novel physics signals. In this context, the clean topologies of exclusive particle production in \peripheral" p p processes mediated by colourless exchanges { such as di-gluon colour-singlet states (aka \Pomerons") or two photons (Fig. 1, left) { is attracting increasing interest despite their much smaller cross sections, O(10−5) less, compared to the standard parton-parton interactions. Exclusive events are characterised by wide rapidity gaps (i.e. a large regions devoid of hadronic activity) on both sides of the centrally produced system and the survival of both protons scattered at very low angles with respect to the beam. The final-state is thus much cleaner, with a larger signal/background and the event kinematics can be constrained measuring the final protons. A prime process of interest at the LHC is the Central Exclusive Production (CEP) of the Higgs boson, pp p H p, (` ' represents a rapidity-gap).
    [Show full text]
  • Status and Perspectives of the Neutron Time-Of-Flight Facility N TOF at CERN
    Status and perspectives of the neutron time-of-flight facility n_TOF at CERN E. Chiaveri on behalf of the n_TOF Collaboration ([email protected]) Since the start of its operation in 2001, based on an idea of Prof. Carlo Rubbia[1], the neutron time-of-flight facility of CERN, n_TOF, has become one of the most forefront neutron facilities in the world for wide-energy spectrum neutron cross section measurements. Thanks to the combination of excellent neutron energy resolution and high instantaneous neutron flux available in the two experimental areas, the second of which has been constructed in 2014, n_TOF is providing a wealth of new data on neutron-induced reactions of interest for nuclear astrophysics, advanced nuclear technologies and medical applications. The unique features of the facility will continue to be exploited in the future, to perform challenging new measurements addressing the still open issues and long-standing quests in the field of neutron physics. In this document the main characteristics of the n_TOF facility and their relevance for neutron studies in the different areas of research will be outlined, addressing the possible future contribution of n_TOF in the fields of nuclear astrophysics, nuclear technologies and medical applications. In addition, the future perspectives of the facility will be described including the upgrade of the spallation target. 1 Introduction Neutron-induced reactions play a fundamental role for a number of research fields, from the origin of chemical elements in stars, to basic nuclear physics, to applications in advanced nuclear technology for energy, dosimetry, medicine and space science [1]. Thanks to the time-of-flight technique coupled with the characteristics of the CERN n_TOF beam-lines and neutron source, reaction cross-sections can be measured with a very high energy-resolution and in a broad neutron energy range from thermal up to GeV.
    [Show full text]
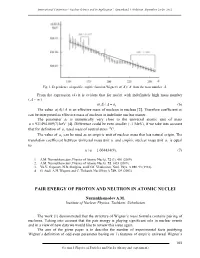
  • Pair Energy of Proton and Neutron in Atomic Nuclei
    International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again.
    [Show full text]
  • 1 PROF. CHHANDA SAMANTA, Phd PAPERS in PEER REVIEWED INTERNATIONAL JOURNALS: 1. C. Samanta, T. A. Schmitt, “Binding, Bonding A
    PROF. CHHANDA SAMANTA, PhD PAPERS IN PEER REVIEWED INTERNATIONAL JOURNALS: 1. C. Samanta, T. A. Schmitt, “Binding, bonding and charge symmetry breaking in Λ- hypernuclei”, arXiv:1710.08036v2 [nucl-th] (to be published) 2. T. A. Schmitt, C. Samanta, “A-dependence of -bond and charge symmetry energies”, EPJ Web Conf. 182, 03012 (2018) 3. Chhanda Samanta, Superheavy Nuclei to Hypernuclei: A Tribute to Walter Greiner, EPJ Web Conf. 182, 02107 (2018) 4. C. Samanta with X Qiu, L Tang, C Chen, et al., “Direct measurements of the lifetime of medium-heavy hypernuclei”, Nucl. Phys. A973, 116 (2018); arXiv:1212.1133 [nucl-ex] 5. C. Samanta with with S. Mukhopadhyay, D. Atta, K. Imam, D. N. Basu, “Static and rotating hadronic stars mixed with self-interacting fermionic Asymmetric Dark Matter”, The European Physical Journal C.77:440 (2017); arXiv:1612.07093v1 6. C. Samanta with R. Honda, M. Agnello, J. K. Ahn et al, “Missing-mass spectroscopy with 6 − + 6 the Li(π ,K )X reaction to search for ΛH”, Phys. Rev. C 96, 014005 (2017); arXiv:1703.00623v2 [nucl-ex] 7. C. Samanta with T. Gogami, C. Chen, D. Kawama et al., “Spectroscopy of the neutron-rich 7 hypernucleus He from electron scattering”, Phys. Rev. C94, 021302(R) (2016); arXiv:1606.09157 8. C. Samanta with T. Gogami, C. Chen, D. Kawama,et al., ”High Resolution Spectroscopic 10 Study of ΛBe”, Phys. Rev. C93, 034314(2016); arXiv:1511.04801v1[nucl-ex] 9. C. Samanta with L. Tang, C. Chen, T. Gogami et al., “The experiments with the High 12 Resolution Kaon Spectrometer at JLab Hall C and the new spectroscopy of ΛB hypernuclei, Phys.
    [Show full text]
  • Current Status of Equation of State in Nuclear Matter and Neutron Stars
    Open Issues in Understanding Core Collapse Supernovae June 22-24, 2004 Current Status of Equation of State in Nuclear Matter and Neutron Stars J.R.Stone1,2, J.C. Miller1,3 and W.G.Newton1 1 Oxford University, Oxford, UK 2Physics Division, ORNL, Oak Ridge, TN 3 SISSA, Trieste, Italy Outline 1. General properties of EOS in nuclear matter 2. Classification according to models of N-N interaction 3. Examples of EOS – sensitivity to the choice of N-N interaction 4. Consequences for supernova simulations 5. Constraints on EOS 6. High density nuclear matter (HDNM) 7. New developments Equation of State is derived from a known dependence of energy per particle of a system on particle number density: EA/(==En) or F/AF(n) I. E ( or Boltzman free energy F = E-TS for system at finite temperature) is constructed in a form of effective energy functional (Hamiltonian, Lagrangian, DFT/EFT functional or an empirical form) II. An equilibrium state of matter is found at each density n by minimization of E (n) or F (n) III. All other related quantities like e.g. pressure P, incompressibility K or entropy s are calculated as derivatives of E or F at equilibrium: 2 ∂E ()n ∂F ()n Pn()= n sn()=− | ∂n ∂T nY, p ∂∂P()nnEE() ∂2 ()n Kn()==9 18n +9n2 ∂∂nn∂n2 IV. Use as input for model simulations (Very) schematic sequence of equilibrium phases of nuclear matter as a function of density: <~2x10-4fm-3 ~2x10-4 fm-3 ~0.06 fm-3 Nuclei in Nuclei in Neutron electron gas + ‘Pasta phase’ Electron gas ~0.1 fm-3 0.3-0.5 fm-3 >0.5 fm-3 Nucleons + n,p,e,µ heavy baryons Quarks ???
    [Show full text]
  • An Analysis on Single and Central Diffractive Heavy Flavour Production at Hadron Colliders
    416 Brazilian Journal of Physics, vol. 38, no. 3B, September, 2008 An Analysis on Single and Central Diffractive Heavy Flavour Production at Hadron Colliders M. V. T. Machado Universidade Federal do Pampa, Centro de Cienciasˆ Exatas e Tecnologicas´ Campus de Bage,´ Rua Carlos Barbosa, CEP 96400-970, Bage,´ RS, Brazil (Received on 20 March, 2008) In this contribution results from a phenomenological analysis for the diffractive hadroproduction of heavy flavors at high energies are reported. Diffractive production of charm, bottom and top are calculated using the Regge factorization, taking into account recent experimental determination of the diffractive parton density functions in Pomeron by the H1 Collaboration at DESY-HERA. In addition, multiple-Pomeron corrections are considered through the rapidity gap survival probability factor. We give numerical predictions for single diffrac- tive as well as double Pomeron exchange (DPE) cross sections, which agree with the available data for diffractive production of charm and beauty. We make estimates which could be compared to future measurements at the LHC. Keywords: Heavy flavour production; Pomeron physics; Single diffraction; Quantum Chromodynamics 1. INTRODUCTION the diffractive quarkonium production, which is now sensitive to the gluon content of the Pomeron at small-x and may be For a long time, diffractive processes in hadron collisions particularly useful in studying the different mechanisms for have been described by Regge theory in terms of the exchange quarkonium production. of a Pomeron with vacuum quantum numbers [1]. However, the nature of the Pomeron and its reaction mechanisms are In order to do so, we will use the hard diffractive factoriza- not completely known.
    [Show full text]