DOCSLIB.ORG

Model Reduction in Chemical Engineering Case Studies Applied to Process Analysis Design and Operation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Model Reduction in Chemical Engineering Case Studies Applied to Process Analysis Design and Operation Model Reduction in Chemical Engineering Case studies applied to process analysis design and operation Cover design by JM&BD Model Reduction in Chemical Engineering Case studies applied to process analysis design and operation Proefschrift ter verkrijging van de graad van doctor aan de Technische Universiteit Delft, op gezag van de Rector Magnificus, prof. ir. K.C.A.M. Luyben, voorzitter van het College voor Promoties in het openbaar te verdedigen op maandag 4 juli 2010 om 15:00 uur door Bogdan DORNEANU Inginer diplomat (Universitatea Politehnica din Bucureşti, Roemenië) geboren te Medgidia (Roemenië) Dit proefschrift is goedgekeurd door de promotor: Prof. ir. J. Grievink Samenstelling promotiecommissie: Rector Magnificus Voorzitter Prof. ir. J. Grievink Technische Universiteit Delft, promotor Dr. ir. C.S. Bildea University Politehnica of Bucharest, copromotor Prof. dr. ir. P.M.J. van den Hof Technische Universiteit Delft Prof. dr. F. Kapteijn Technische Universiteit Delft Dr. ir. H.J.M. Kramer Technische Universiteit Delft Prof. dr. ir. P.M.M. Bongers Technische Universiteit Eindhoven / Unilever Prof. dr. P.D. Iedema Universiteit van Amsterdam Dr. ir. P.J.T. Verheijen Technische Universiteit Delft, reservelid Keywords: model reduction, process modelling, plantwide control, dynamic optimization, alkylation, ice cream freezing An electronic version of this thesis is available from http://www.library.tudelft.nl ISBN 978-90-8570-771-4 Copyright ©2011 by Bogdan Dorneanu All rights reserved. No part of the material protected by this copyright notice may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage and retrieval system, without the prior written permission from the author. Printed in The Netherlands by CPI Wöhrmann Print Service Motto “It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.” A. Einstein A significant part of the research was carried out within the framework of MRTN-CT-2004-512233 (PRISM – Towards Knowledge-Based Processing Systems). The financial support of the European Commission and Unilever R&D Vlaardingen is gratefully acknowledged. Table of contents Summary ............................................................................................................................................... i Samenvatting ....................................................................................................................................... v Rezumat............................................................................................................................................... ix Chapter 1 – Introduction .................................................................................................................... 1 1. Role of modelling in chemical engineering ................................................................................... 2 1.1. Model applications and benefits ....................................................................................... 2 1.2. Efforts and cost factors for model development and application ...................................... 5 2. Requirements for model use in chemical engineering ................................................................... 5 3. Process models and modelling ....................................................................................................... 6 3.1. Process models ................................................................................................................. 6 3.2. Model classification ......................................................................................................... 8 3.3. Model development steps ................................................................................................. 9 3.4. Dual way of modelling: decomposition and aggregation over detail levels.................... 13 4. Motivation and formulation of the research problem ................................................................... 15 5. Research approach and outline of the thesis ................................................................................ 18 6. References ................................................................................................................................... 20 Chapter 2 – Process modelling and model reduction ..................................................................... 25 1. Introduction ................................................................................................................................. 26 2. A design view on process modelling ........................................................................................... 27 2.1. Levels of decomposition in the modelling procedure ..................................................... 28 3. Contextual and structure levels of decomposition ....................................................................... 30 3.1. Contextual level .............................................................................................................. 30 3.2. Structure level ................................................................................................................ 31 3.2.1. Process decomposition and physical structure of the model ........................................... 31 3.2.2. Behavioural structure of the model ................................................................................. 36 3.2.3. Model connectivity ......................................................................................................... 37 4. Mathematical, numerical and software implementation levels .................................................... 39 4.1. Mathematical level: behavioural models of nodes .......................................................... 40 4.1.1. Coordinates ..................................................................................................................... 40 4.1.2. Classification of quantities .............................................................................................. 41 4.1.3. Classification of equations .............................................................................................. 42 4.1.4. Validity and applicability conditions (knowledge constraints) ....................................... 46 4.1.5. Types of operations in model equations .......................................................................... 46 4.1.6. Model classification ........................................................................................................ 46 4.2. Mathematical level: Connectivity ................................................................................... 47 4.3. Mathematical level: Aggregation at system level ........................................................... 49 4.4. Relationship between the structure and the complexity of the model ............................. 51 4.4.1. Number of equations ....................................................................................................... 52 4.4.2. Number of terms in the model equations ........................................................................ 52 4.4.3. Connectivity of the model equations ............................................................................... 53 4.5. Numerical level .............................................................................................................. 53 4.6. Software implementation level ....................................................................................... 54 5. Existent model reduction techniques ........................................................................................... 55 5.1. Approaches to model reduction of process models ........................................................ 55 5.2. Contextual level .............................................................................................................. 55 5.3. Structure level ................................................................................................................ 56 5.3.1. Model reduction at physical structure level ..................................................................... 56 5.3.2. Model reduction at behavioural structure level ............................................................... 58 5.4. Mathematical level ......................................................................................................... 59 5.4.1. Model simplification techniques ..................................................................................... 60 5.4.2. Model order-reduction techniques ................................................................................... 61 5.5. System level ................................................................................................................... 62 5.6. Numerical level .............................................................................................................. 62 6. Model reduction for chemical engineering applications .............................................................. 63 7. Selected research problems in model reduction ........................................................................... 64 8. Conclusions ................................................................................................................................
Load more

Recommended publications
  • Yntbietic Fnei
    23c$b/J jflt yntbietic fnei OIL SHALE 0 COAL 0 OIL SANDS VOLUME 24 — NUMBER 3 — SEPTEMBER 1987 QUARTERLY Toll Eril Reposito,y ,.r;.'.ur Lakas Library csdo School of Mcs © THE PACE CONSULTANTS INC. 0 Reg. U.S. Pal. OFF. Pace Synthetic Fuels Report Is published by The Pace Consultants Inc., as a multi-client service and is intended for the sole use of the clients or organizations affiliated with clients by virtue of a relationship equivalent to 51 percent or greater ownership. Pace Synthetic Fuels Report is protected by the copyright laws of the United States; reproduction of any part of the publication requires the express permission of The Pace Con- sultants Inc. The Pace Consultants Inc., has provided energy consulting and engineering services since 1955. The company's experience includes resource evalua- tion, process development and design, systems planning, marketing studies, licenser comparisons, environmental planning, and economic analysis. The Synthetic Fuels Analysis group prepares a variety of periodic and other reports analyzing developments in the energy field. THE PACE CONSULTANTS INC. SYNTHETIC FUELS ANALYSIS MANAGING EDITOR Jerry E. Sinor Pt Office Box 649 Niwot, Colorado 80544 (303) 652-2632 BUSINESS MANAGER Ronald L. Gist Post Office Box 53473 Houston, Texas 77052 (713) 669-8800 Telex: 77-4350 CONTENTS HIGHLIGHTS A-i I. GENERAL CORPORATIONS Gill Cuts Coal Gasification Programs 1-i API Data Shows Drop in Oil Production 1-4 GOVERNMENT Petroleum Research Institute Proposed i-S FERC Kills Incremental Gas Pricing 1-5 California to Fund Advanced Energy Technologies i_s ERAB Studying Energy Competitiveness 1-6 ENERGY POLICY AND FORECASTS U.S.
    [Show full text]
  • Green Petroleum Refining - Mathematical Models for Optimizing Petroleum Refining Under Emission Constraints
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of Waterloo's Institutional Repository Green Petroleum Refining - Mathematical Models for Optimizing Petroleum Refining Under Emission Constraints by Yusuf Ali Yusuf A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Applied Science in Chemical Engineering Waterloo, Ontario, Canada, 2013 © Yusuf Ali Yusuf 2013 I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Petroleum refining processes provide the daily requirements of energy for the global market. Each refining process produces wastes that have the capacity to harm the environment if not properly disposed of. The treatment of refinery waste is one of the most complex issues faced by refinery managers. Also, the hazardous nature of these wastes makes them rather costly to dispose of for the refineries. In this thesis, system analysis tools are used to design a program that allows for the selection of the optimal control, minimization and treating options for petroleum refinery waste streams. The performance of the developed model is demonstrated via a case study. Optimal mitigation alternatives to meet the emission reduction targets were studied by evaluating their relative impact on the profitable operation of the given facility. It was found that the optimal mitigation steps was to reduce emission precursors by conducting feed switches at the refinery.
    [Show full text]
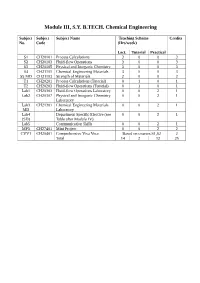
  • Module III, S.Y. B.TECH. Chemical Engineering
    Module III, S.Y. B.TECH. Chemical Engineering Subject Subject Subject Name Teaching Scheme Credits No. Code (Hrs/week) Lect. Tutorial Practical S1 CH20101 Process Calculations 3 0 0 3 S2 CH20103 Fluid-flow Operations 3 0 0 3 S3 CH20105 Physical and Inorganic Chemistry 3 0 0 3 S4 CH21101 Chemical Engineering Materials 3 0 0 3 S5 MD CH21103 Strength of Materials 2 0 0 2 T1 CH20201 Process Calculations (Tutorial) 0 1 0 1 T2 CH20203 Fluid-flow Operations (Tutorial) 0 1 0 1 Lab1 CH20303 Fluid-flow Operations Laboratory 0 0 2 1 Lab2 CH20307 Physical and Inorganic Chemistry 0 0 2 1 Laboratory Lab3 CH21301 Chemical Engineering Materials 0 0 2 1 MD Laboratory Lab4 Department Specific Elective (see 0 0 2 1 (SD) Table after Module IV) Lab5 Communication Skills 0 0 2 1 MP3 CH27401 Mini Project 0 0 2 2 CVV1 CH20401 Comprehensive Viva Voce Based on courses S1,S2 2 Total 14 2 12 25 Issue 05: Rev No. 1: Dt. 30/03/15 FF No: 654A CH 20101:: PROCESS CALCULATIONS Credits: 03 Teaching Scheme: 3 Hours / Week Unit I: Basic Chemical Calculations (8 Hrs) A. Dimensions and Units, chemical calculations including mole, equivalent weight, solids, liquids, solutions and their properties, properties of gases. B. Significance Unit conversions of mass, energy and pressure Unit II: Material Balances Without Chemical Reactions (8 Hrs) A. Process flow sheet, Concept, Material balance calculations, recycling and bypassing operations, material balance of unsteady state processes. B. Material balance of unit operations such as distillation, crystallization Unit III: Material Balances Involving Chemical Reactions (8 Hrs) A.
    [Show full text]
  • When Chemical Reactors Were Admitted and Earlier Roots of Chemical Engineering
    When Chemical Reactors Were Admitted And Earlier Roots of Chemical Engineering 9 Biographical sketch of L. E. ‘Skip’ Scriven L. E. 'Skip' Scriven is Regents' Professor and holder of the L E Scriven Chair of Chemical Engineering & Materials Science at the University of Minnesota. He is a Fellow of the Minnesota Supercomputer Institute, founded the Coating Process Fundamentals Program, and now co-leads it with Professor Lorraine F. Francis. He is distinguished for pioneering researches in several areas of fluid mechanics, interfacial phenomena, porous media and surfactant technologies, and the recently emerged field of coating science and engineering. He promoted close interactions with industry by showing how good theory, incisive experimental techniques, and modern computer-aided mathematics can be combined to solve industrial processing problems. He graduated from the University of California, Berkeley, received a Ph.D. from the University of Delaware, and was a research engineer with Shell Development Company for four years before joining the University of Minnesota. He received the AIChE Allan P. Colburn Award four decades ago, the William H. Walker Award two decades ago, the Tallmadge Award in 1992, and the Founders Award in 1997. He has also been honored by the University of Minnesota and the American Society for Engineering Education for outstanding teaching. He has co-advised or advised many undergraduate, graduate and postdoctoral research students, including over 100 Ph.D.’s. Elected to the National Academy of Engineering in 1978, he has served on several U.S. national committees setting priorities for chemical engineering and materials science research. In 1990-92 he co-chaired the National Research Council's Board on Chemical Sciences and Technology, and in 1994-97 he served on the governing Commission on Physical Sciences, Mathematics, and Applications.
    [Show full text]
  • PROCESS HEAT TRANSFER Course Code CH 4001 Course Title PROCESS HEAT TRANSFER Number of Credits 3 (L-2,T-1, P-0) Prerequisites NIL Course Category PC
    Chemical Engineering IVSemester Prepared :2020-21 PROCESS HEAT TRANSFER Course Code CH 4001 Course Title PROCESS HEAT TRANSFER Number of Credits 3 (L-2,T-1, P-0) Prerequisites NIL Course Category PC COURSE LEARNING OBJECTIVES: • To study the fundamental concepts of heat transfer viz., conduction, convection and radiation. • To use these fundamentals in typical engineering applications (Heat exchanger and Evapora tor). COURSE OUTCOMES: On completion of the course, the student can able • to estimate steady state heat transfer rates. • to use equations for different types of convection and solve for heat transfer rate by convection •to estimate the rate of heat transfer by radiation •to estimate steam economy, capacity of single and multiple effect evaporators. COURSE CONTENTS: 1. CONDUCTION 1.1 Basic modes of heat transfer 1.2 Fourier's law of heatconduction 1.2.1 General heat conduction equations 1.2.2 Unsteady state conduction 1.2.3 Steady state conduction 1.3 Heat flow equation for composite wall 1.4 Concepts of thermal diffusivity 1.5 Heat flow equation for composite cylinder 1.6 Optimum insulation thickness 2. CONVECTION 2.1 Introduction to convection 2.2 Types of convection 2.3 Dimensional analysis 2.3.1 Criteria ofSimilitude 2.3.2 Advantages and limitations of dimensionalanalysis 2.4 Dimensionless number for heat transfer and their physicalsignificance 3. RADIATION 3.1 Thermal Radiation laws 3.2 Radiant energy distribution curve 3.3 Black and Gray bodies 3.4 Boiling 3.4.1 Boiling Phenomenon 3.4.2 Hysteresis in boiling curve 3.5 Condensation 3.5.1 Types 3.5.2 Condensation of super heated vapors 1 Chemical Engineering IVSemester Prepared :2020-21 4.
    [Show full text]
  • Unit Operation
    Unit OperatiOn What is chemical engineering? Chemical Engineering is a group of industrial processes in which row materials are changed or separated into useful products What are "Unit Operations"? Every industrial chemical process is based on Unit Operations (physical treatment) and Unit Process (chemical treatment) to produce economically a desired product from specific raw materials. The raw materials are treated through physical steps to make it suitable for chemical reaction. So, knowledge of unit operations like ‘Mixing and agitation of liquid’ and’ heat flow’ is very much necessary. The subject Unit Operations is based on fundamental laws, physicochemical principles. Unit Operations gives idea about science related to specific physical operation; Lecturer . Shymaa Ali Hameed 2013-2014 Unit OperatiOn different equipments-its design, material of construction and operation; and calculation of various physical parameters (mass flow, heat flow, mass balance, power and force etc.). Examples of Unit Operations are listed in Table 1. Table 1: List of some unit operations Heat flow, Fluid flow Mixing Drying Absorption Evaporation Adsorption Distillation Condensation Crystallization Vaporization Leaching Separation Extraction Sedimentation Filtration Crushing Following are some examples of physical processes : 1) Sugar Manufacture: Sugar cane crushing → sugar extraction → thickening of syrup →evaporation of water → sugar crystallization → filtration →drying →screening →packing 2) Salt Manufacture: Brine transportation → evaporation → crystallization →drying → screening → conveying → packaging. 3) Pharmaceutical Manufacture: Formulation of chemicals, mixing, granulation → drying of granules→ screening → pressing tablet → packaging Lecturer . Shymaa Ali Hameed 2013-2014 Unit OperatiOn The equipment used in the chemical processes industries can be divided into two classes:. 1. Proprietary equipment, such as pumps, compressors, filters, centrifuges and dryers, is designed and manufactured by specialist firms.
    [Show full text]
  • NPTEL Syllabus
    NPTEL Syllabus Process Modelling and Simulation - Web course COURSE OUTLINE The Process Modeling and Simulation of Chemical engineering processes has attracted the attention of scientists and NPTEL engineers for many decades and is still a subject of major http://nptel.ac.in importance for the knowledge of unitary processes of transport and kinetics. Basically it deals with three aspects, namely; Modeling of Chemical chemical engineering processes, parameter estimations and application of numerical methods for solution of models. Engineering In this course first chapter is devoted to introduction of the course and discusses the simulation and need of simulation. Subsequently it follows the parameter estimation, tools of Pre-requisites: simulation, development of models, classification of models, unit models of unit process, models of heat transfer equipment, Basic knowledge of Courses separation processes and reactors, and application of on Material & Energy Balance; numerical methods for solutions of models. Transport Phenomena and Numerical methods. Contents: Additional Reading: Process simulation, tools of simulation, parameter estimation, models and classification of models, alternate classification of models, mathematical modeling based on transport Standards software of phenomena, population balance, principles of probability and simulation. experimental data. Coordinators: Unit models of unit processes, detailed mathematical models of heat transfer equipment, separation processes, reactors, Dr. V. K. Agrawal numerical methods for solution of mathematical models in the Department of Chemical form of partial differential equations. EngineeringIIT Roorkee COURSE DETAIL S.No Topics No. of Hours 1 Introduction : 3 Introduction to process modeling and simulation, tools of simulation, approaches of simulation, planning of calculation in a plant simulation. 2 Parameter Estimation: 3 Parameter estimation techniques in theoretical as well as numerical models.
    [Show full text]
  • Model-Based Integrated Process Design and Controller Design of Chemical Processes
    Downloaded from orbit.dtu.dk on: Oct 26, 2019 Model-Based Integrated Process Design and Controller Design of Chemical Processes Abd Hamid, Mohd Kamaruddin Bin Publication date: 2011 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Abd Hamid, M. K. B. (2011). Model-Based Integrated Process Design and Controller Design of Chemical Processes. Kgs. Lyngby, Denmark: Technical University of Denmark. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. Users may download and print one copy of any publication from the public portal for the purpose of private study or research. You may not further distribute the material or use it for any profit-making activity or commercial gain You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Model-Based Integrated Process Design and Controller Design of Chemical Processes Mohd. Kamaruddin bin Abd. Hamid Ph.D. Thesis January 2011 Model-Based Integrated Process Design and Controller Design of Chemical Processes Ph.D. Thesis Mohd. Kamaruddin bin Abd. Hamid January 2011 Computer Aided Process-Product Engineering Center Department of Chemical and Biochemical Engineering Technical University of Denmark Copyright©: Mohd. Kamaruddin bin Abd. Hamid January 2011 Address: Computer Aided Process Engineering Center Department of Chemical and Biochemical Engineering Technical University of Denmark Building 229 DK-2800 Kgs.
    [Show full text]
  • Pharmaceutical Engineering
    PHARMACEUTICAL ENGINEERING Unit Operations and Unit Processes Dr Jasmina Khanam Reader of Pharmaceutical Engineering Division Department of Pharmaceutical Technology Jadavpur University Kolkatta-700032 (06-11-2007) CONTENTS Introduction Unit Systems Material Balance Energy Balance Ideal gas law Gaseous Mixtures Dimensional analysis Graph plotting Graphical Integration Graphical differentiation Ternary Plot 1 Introduction Every industrial chemical process is based on Unit Operations (physical treatment) and Unit Process (chemical treatment) to produce economically a desired product from specific raw materials. The raw materials are treated through physical steps to make it suitable for chemical reaction. So, knowledge of unit operations like ‘Mixing and agitation of liquid’ and’ heat flow’ is very much necessary. The subject Unit Operations is based on fundamental laws, physicochemical principles. Unit Operations gives idea about science related to specific physical operation; different equipments-its design, material of construction and operation; and calculation of various physical parameters (mass flow, heat flow, mass balance, power and force etc.). Examples of Unit Operations are listed in Table 1. Table 1: List of some unit operations Heat flow, Fluid flow Mixing Drying Absorption Evaporation Adsorption Distillation Condensation Crystallization Vaporization Leaching Separation Extraction Sedimentation Filtration Crushing After preparing raw materials by physical treatment, these undergo chemical conversion in a reactor. To perform chemical conversion basic knowledge of stoichiometry, reaction kinetics, thermodynamics, chemical equilibrium, energy balance and mass balance is necessary. Many alternatives may be proposed to design a reactor for a chemical process. One design may have low reactor cost, but the final materials leaving the unit need higher treatment cost while separating and purifying the desired product.
    [Show full text]
  • UNIT OPERATION the Basic Physical Operations of Chemical Engineering
    UNIT OPERATION The basic physical operations of chemical engineering in a chemical process plant, that is distillation, fluid transportation, heat and mass transfer, evaporation, extraction, drying, crystallization, filtration, mixing, size separation, crushing and grinding, and conveying. In simple terms, the operation which involves physical changes are known as Unit Operation. 1. Distillation is a unit operation is used to purify or separate alcohol in the brewery industry. 2. The same distillation separates the hydrocarbon in a petroleum industries. 3. Dry grapes and other food products or similar drying of filter precipitate like rayon industry where yarn is produced. 4. Absorption of oxygen from air in a fermentation process of a sewage treatment plant and half hydrogen gas in a process for liquid hydrogenation of oil. 5. Evaporation of salts solutions similar to evaporation of sugar solution in the industry. 6. Settling and sedimentation of suspend solids similar to minimizing and sewage treatment plant. 7. Flow of liquid hydrocarbon in a petroleum refinery and flow of milk in a daily plant for the solidification in spray dryer. Classification of Unit Operations 1. Fluid Flow : Concerns the principle that determine the flow or transformation of fluids from one point to another. The fluid can be a liquid or a gas. This unit is entirely based on Bernoulli e's equation followed by continuity correlation. 2. Heat Transfer : Deals with principles that govern accumulation and transfer of heat and energy from one place to another. The three concepts followed here are conduction, convection and radiation. 3. Evaporation : A special case of heat transfer which deals with the evaporation of volatile solvent such as waste from a non-volatile solute such as salt or any other material in the solution.
    [Show full text]
  • Copyright and Citation Considerations for This Thesis/ Dissertation
    COPYRIGHT AND CITATION CONSIDERATIONS FOR THIS THESIS/ DISSERTATION o Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. o NonCommercial — You may not use the material for commercial purposes. o ShareAlike — If you remix, transform, or build upon the material, you must distribute your contributions under the same license as the original. How to cite this thesis Surname, Initial(s). (2012) Title of the thesis or dissertation. PhD. (Chemistry)/ M.Sc. (Physics)/ M.A. (Philosophy)/M.Com. (Finance) etc. [Unpublished]: University of Johannesburg. Retrieved from: https://ujcontent.uj.ac.za/vital/access/manager/Index?site_name=Research%20Output (Accessed: Date). ATTAINABLE REGIONS FOR OPTIMAL REACTION NETWORKS: APPLICATION OF ΔH-ΔG PLOT TO DIRECT SYNTHESIS OF DIMETHYL ETHER FROM SYNGAS By THULANE PAEPAE Submitted In Fulfilment of the Requirements of MASTERS TECHNOLOGIAE In CHEMICAL ENGINEERING In the FACULTY OF ENGINEERING AND THE BUILT ENVIRONMENT Of the UNIVERSITY OF JOHANNESBURG Supervisor: Dr Tumisang Seodigeng Co-supervisor: Prof Freeman Ntuli Johannesburg, 2015 DECLARATION I hereby declare that this dissertation which I submit in fulfilment for the qualification MAGISTER OF TECHNOLOGIAE IN CHEMICAL ENGINEERING to the University of Johannesburg, Department of Chemical Engineering is, apart from the recognized assistance from my supervisors, my own work which has not previously been submitted by me or any other person to any institution to obtain a degree. On this Day of i ABSTRACT Industrial processes pose a serious threat to the world’s natural resources for they consume them in high proportions as sources of energy for driving chemical processes that provide raw materials for many industrial chemicals.
    [Show full text]
  • I Unit Operations
    Unit – I Unit Operations Introduction to process & Instrumentation for Chemical • Chemical Process Control and Instrumentation • Automatic and Instrument control chemical processes are common and essential. Instruments should not be chosen simply to record a variables, of the process. But their function is to assure consistent quality by sensing controls, recording and maintaining desired operating conditions. Instruments are the essential tool for modern processes. They are classified as • Indicating Instruments • Recording Instruments • Controlling Instruments Unit Operation Basic Instrumentation 2 Continuous-flow stirred-tank reactor (CSTR) • In a continuous-flow stirred-tank reactor (CSTR), reactants and products are continuously added and withdrawn. • In practice, mechanical or hydraulic agitation is required to achieve uniform composition and temperature, a choice strongly influenced by process considerations. • The CSTR is the idealized opposite of the well-stirred batch and tubular plug-flow reactors. • Analysis of selected combinations of these reactor types can be useful in quantitatively evaluating more complex gas-, liquid-, and solid-flow behaviors. Unit Operation Basic Instrumentation 3 Continuous-flow stirred-tank reactor (CSTR) Unit Operation Basic Instrumentation 4 Continuous-flow stirred-tank reactor (CSTR) • Roll of Instrumentation Engineering • Measurement and control of tank and jacket Temperature • Measurement and control of tank level • Measurement and control of inlet and outlet flow • Measurement and control of speed of motor Unit Operation Basic Instrumentation 5 Definitions, application & comparison: Batch Process, Continuous Process Continuous processes • A chemical that is needed in a large amount is usually made by a continuous process. • Production goes on all the time. • Ammonia is made by a continuous process called the Haber process.
    [Show full text]