Uniqueness of Solutions of the Generalized Abel Integral Equations in Banach Spaces
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Azərbaycan Respublikasi Vəkillər Kollegiyasinin Rəyasət Heyəti Board of the Bar Association of the Republic of Azerb
AZƏRBAYCAN RESPUBLİKASI BOARD OF THE VƏKİLLƏR KOLLEGİYASININ BAR ASSOCIATION OF THE RƏYASƏT HEYƏTİ REPUBLIC OF AZERBAIJAN Jeyhun Hajibeyli Str. 100, AZ1007, Baku, Azerbaijan. Tel: 012 594 14 95, E-mail: [email protected] “21” October 2020 № 1028 THE CALL OF THE AZERBAIJANI BAR ASSOCIATION TO ITS INTERNATIONAL COLLEAGUES (See also Enc. Annex) Dear Colleagues! I would like to draw your attention to the fact that for almost 27 years Armenia has been occupying 20% of the territory of the Republic of Azerbaijan, in Nagorno-Karabakh and its surrounding regions. Thus, since 1988, separatist groups have emerged among the Armenian population living in Nagorno-Karabakh under foreign influence and, together with nationalist groups in Yerevan. These groups demanded the annexation of the Nagorno- Karabakh Autonomous Region (hereinafter Nagorno-Karabakh) to Armenia. In addition, 300,000 ethnic Azerbaijanis living in Armenia were expelled from their native lands and became refugees. 1 2 In 1992-1994, besides Nagorno-Karabakh territory, Armenia, with the support of local separatist forces and foreign mercenaries, occupied seven adjacent regions around Nagorno-Karabakh (not part of Nagorno-Karabakh), resulting in the displacement of about 1 million Azerbaijanis living in and around Nagorno-Karabakh. Thousands of innocent civilians were slaughtered, and on February 26, 1992, an act of genocide was committed in the city of Khojaly. 3 4 5 1 https://www.hrw.org/reports/AZER%20Conflict%20in%20N-K%20Dec94_0.pdf 2 https://epress.am/ru/2015/04/29/события-в-гугарке-как-громили-азербай.html -

Revista Dilemas Contemporáneos: Educación, Política Y Valores. Http
1 Revista Dilemas Contemporáneos: Educación, Política y Valores. http://www.dilemascontemporaneoseducacionpoliticayvalores.com/ Año: VII Número: Edición Especial Artículo no.:102 Período: Octubre, 2019. TÍTULO: Las direcciones en el desarrollo del estudio de prensa en Azerbaiyán: contexto histórico y social. AUTOR: 1. Ph.D. Garanfil Guliyeva Dunyamin. RESUMEN: El artículo se centa en el contexto histórico y social de la historia de la prensa de Azerbaiyán, y examina las direcciones en el desarrollo de la prensa. Identifica la tendencia actual en un contexto histórico y social hacia el desarrollo de la prensa. Se están analizando las etapas actuales de las direcciones de desarrollo. Durante el período 1900-2000, se siguen los cambios de período en el desarrollo de la prensa, la dinámica y los antecedentes sociales, y los factores deficiencias actuales que afectan el desarrollo de la prensa, incluidos los efectos del "régimen post- soviético" y "la influencia de los mecanismos de los extraterrestres", elementos que son llevados al centro de atención. El artículo incorpora principios de investigación de vanguardia para aclarar el panorama científico-teórico en el campo del estudio de prensa azerbaiyano. PALABRAS CLAVES: Estudio de prensa azerbaiyano, la era moderna, direcciones de desarrollo, historia y contexto social. TİTLE: The directions in the development of the press study in Azerbaijan: historical and social context. 2 AUTHOR: 1. Ph.D. Garanfil Guliyeva Dunyamin. ABSTRACT: The article focuses on the historical and social context of Azerbaijan's press history, and examines directions in press development. It identifies the current tendency in a historical and social context towards the development of press. -

Liste Des Participants
World Heritage 43 COM WHC/19/43.COM/INF.2 Paris, July/ juillet 2019 Original: English / French UNITED NATIONS EDUCATIONAL, SCIENTIFIC AND CULTURAL ORGANIZATION ORGANISATION DES NATIONS UNIES POUR L'EDUCATION, LA SCIENCE ET LA CULTURE CONVENTION CONCERNING THE PROTECTION OF THE WORLD CULTURAL AND NATURAL HERITAGE CONVENTION CONCERNANT LA PROTECTION DU PATRIMOINE MONDIAL, CULTUREL ET NATUREL WORLD HERITAGE COMMITTEE/ COMITE DU PATRIMOINE MONDIAL Forty-third session / Quarante-troisième session Baku, Republic of Azerbaijan / Bakou, République d’Azerbaïdjan 30 June – 10 July 2019 / 30 juin - 10 juillet 2019 LIST OF PARTICIPANTS LISTE DES PARTICIPANTS This list is based on the information provided by participants themselves, however if you have any corrections, please send an email to: [email protected] Cette liste est établie avec des informations envoyées par les participants, si toutefois vous souhaitez proposer des corrections merci d’envoyer un email à : [email protected] Members of the Committee / Membres du Comité ............................................................ 5 Angola ............................................................................................................................... 5 Australia ............................................................................................................................ 5 Azerbaijan ......................................................................................................................... 7 Bahrain ............................................................................................................................. -

The Piano Music of Azerbaijan: National and Cross- Cultural Influences on Contemporary Performance Practices
City Research Online City, University of London Institutional Repository Citation: Mirzayeva, G. (2020). The piano music of Azerbaijan: national and cross- cultural influences on contemporary performance practices. (Unpublished Doctoral thesis, Guildhall School of Music and Drama) This is the accepted version of the paper. This version of the publication may differ from the final published version. Permanent repository link: https://openaccess.city.ac.uk/id/eprint/25377/ Link to published version: Copyright: City Research Online aims to make research outputs of City, University of London available to a wider audience. Copyright and Moral Rights remain with the author(s) and/or copyright holders. URLs from City Research Online may be freely distributed and linked to. Reuse: Copies of full items can be used for personal research or study, educational, or not-for-profit purposes without prior permission or charge. Provided that the authors, title and full bibliographic details are credited, a hyperlink and/or URL is given for the original metadata page and the content is not changed in any way. City Research Online: http://openaccess.city.ac.uk/ [email protected] The Piano Music of Azerbaijan: National and Cross- Cultural Influences on Contemporary Performance Practices A thesis submitted to Guildhall School of Music & Drama for the degree of DMus in the Department of Research January 2020 Gunel Mirzayeva Table of Contents Table of Contents ii List of Figures and Maps vii Abstract ix Acknowledgments x Abbreviations and Notes on Transliteration -

REPUBLIC of AZERBAIJAN on the Rights of the Manuscript ABSTRACT of the Dissertation for the Degree of Doctor of Philosophy ARTIS
REPUBLIC OF AZERBAIJAN On the rights of the manuscript ABSTRACT of the dissertation for the degree of Doctor of Philosophy ARTISTIC DESCRIPTION OF NATIONAL INDEPENDENCE IDEAS IN AZERBAIJAN SATIRIC PROSE AT THE BEGINNING OF THE XX CENTURY Specialty: 5716.01 – Azerbaijan Literature Field of science: Philology Applicant: Parvin Aghabala gizi Huseynova Baku – 2021 The dissertation was performed at the Department of Azerbaijani and World Literature, Faculty of Philology, Azerbaijan State Pedagogical University Scientific supervisor Academician, Doctor of Philological (consultant): Sciences, Professor Teymur Hashim oglu Kerimli Official opponents: Doctor of Philological Sciences, Professor Vugar Mikayıl oglu Ahmed Doctor of Philological Sciences, Professor Yadulla Babir oglu Aghazade PhD in philology, Associate Professor Elchin Huseyn oglu Mammadov Dissertation council ED 1.05 of Supreme Attestation Commission under the President of the Republic of Azerbaijan operating at the Institute of Literature named after Nizami Ganjavi of ANAS Chairman of the Academician, Doctor of Philological Dissertation council: Sciences, Professor _________________ Isa Akbar oglu Habibbayli Scientific secretary of the Dissertation council: PhD in philology, Associate Professor ________________ Ismikhan Mahammad oglu Osmanli Chairman of the scientific seminar: Doctor of Philological Sciences, Associate Professor _________________ Alizade Bayram oglu Asgarli GENERAL CHARACTERISTICS OF THE RESEARCH Relevance of topic and extent of doing the research. The literature of the late nineteenth and early twentieth centuries, reflecting the interests of the people, was a mirror of its glorious history, a carrier of nationalist ideas, and united its readers around humanistic ideals and the ideology of independence. It is well known that the ideological invasion pursued by the state policy in Russia and Iran after the Gulustan and Turkmenchay treaties aimed at destroying the national self-consciousness of our people was ineffective. -

Modernleşme Teorileri Açisindan Azerbaycan Modernleşmesinin Değerlendirilmesi
T.C. İSTANBUL 29 MAYIS ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ SİYASET BİLİMİ VE ULUSLARARASI İLİŞKİLER ANABİLİM DALI MODERNLEŞME TEORİLERİ AÇISINDAN AZERBAYCAN MODERNLEŞMESİNİN DEĞERLENDİRİLMESİ ASSESSING AZERBAIJAN’S MODERNIZATION TRAJECTORY IN LIGHT OF THEORIES OF MODERNITY (YÜKSEK LİSANS TEZİ) Javadbay KHALILZADA Danışman: Yrd. Doç. Dr. Oğuzhan GÖKSEL İSTANBUL - 2016 İSTANBUL 29 MAYIS ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ SİYASET BİLİMİ VE ULUSLARARASI İLİŞKİLER ANABİLİM DALI MODERNLEŞME TEORİLERİ AÇISINDAN AZERBAYCAN MODERNLEŞMESİNİN DEĞERLENDİRİLMESİ (YÜKSEK LİSANS TEZİ) Javadbay KHALILZADA Danışman: Yrd. Doç. Dr. Oğuzhan GÖKSEL İSTANBUL - 2016 T. C. İSTANBUL 29 MAYIS ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ MÜDÜRLÜĞÜNE Siyaset Bilimi ve Uluslararası İlişkiler Anabilim Dalı, Siyaset Bilimi ve Uluslararası İlişkiler Bilim Dalı’nda 030114YL01 numaralı Javadbay Khalilzada’nın hazırladığı Assessing Azerbaıjan’s Modernization Trajectory In Light of Theories of Modernity konulu Yüksek Lisans Tezi ile ilgili tez savunma sınavı, 21/07/2016 günü 14.00- 15.30 saatleri arasında yapılmış, sorulan sorulara alınan cevaplar sonunda adayın tezinin başarılı olduğuna oybirliği ile karar verilmiştir. Yrd. Doç. Dr. Oğuzhan GÖKSEL Prof. Dr. Michelangelo GUİDA İstanbul 29 Mayıs Üniversitesi İstanbul 29 Mayıs Üniversitesi (Tez Danışmanı ve Sınav Komisyonu Başkanı) Yrd. Doç. Dr. Zübeyir Nişancı İstanbul Şehir Üniversitesi DECLARATION I hereby declare that all information in this study has been obtained and presented in accordance with academic rules and -

The Idea of Independence in the Literature of the Republican Period
Вчені записки ТНУ імені В. І. Вернадського. Серія: Філологія. Соціальні комунікації UDC 82 DOI https://doi.org/10.32838/2663-6069/2020.3-2/41 Rustamkhanli T. Institute of Literature named after Nizami Ganjavi THE IDEA OF INDEPENDENCE IN THE LITERATURE OF THE REPUBLICAN PERIOD At the beginning of the twentieth century another idea came to Turanism, and we can say with full responsibility that Azerbaijan has never experienced a rich cycle of ideas as in the early 20th century. The Azerbaijani literature showed the greatest heroism in fostering a sense of identity to the nation by not only competing with the political power of Azerbaijan, but also struggling for its independence. Azerbaijani literary criticism and study of literary also went through a long way in the Republican Period. Generally, most intellectuals of Azerbaijan at that time, along with the state building, wrote articles, books and published them in European countries to promote Azerbaijani literature, culture, art, history and ethnography. The Azerbaijan Democratic Republic has brought independence and freedom to the people, causing a revolutionary leap in public consciousness, morality, literature, art, and culture and though the most totalitarian regime in the world turned on all repressive machines, it could not erase it from memory. Though the written books, newspapers and articles were burned and destroyed, the seeds of independence that sank into hearts and minds raised again and led to the Independent Azerbaijan Republic. No matter how deep and ancient the history of the idea of national independence of the Azerbaijani people is, its history of research is much shorter. -

ISSN: 2051-0861 Publication Details, Including Guidelines for Submissions
ISSN: 2051-0861 Publication details, including guidelines for submissions: https://journals.le.ac.uk/ojs1/index.php/nmes Modernization and Social Change in Azerbaijan: Assessing the Transformation of Azerbaijan through the Theories of Modernity Author(s): Javadbay Khalilzada To cite this article: Khalilzada, Javadbay (2019) “Modernization and Social Change in Azerbaijan: Assessing the Transformation of Azerbaijan through the Theories of Modernity”, New Middle Eastern Studies 9 (2), pp. 167-188. Online Publication Date: 30 September 2019 Disclaimer and Copyright The NMES editors make every effort to ensure the accuracy of all the information contained in the journal. However, the Editors and the University of Leicester make no representations or warranties whatsoever as to the accuracy, completeness or suitability for any purpose of the content and disclaim all such representations and warranties whether express or implied to the maximum extent permitted by law. Any views expressed in this publication are the views of the authors and not the views of the Editors or the University of Leicester. Copyright New Middle Eastern Studies, 2019. All rights reserved. No part of this publication may be reproduced, stored, transmitted or disseminated, in any form, or by any means, without prior written permission from New Middle Eastern Studies, to whom all requests to reproduce copyright material should be directed, in writing. Terms and Conditions This article may be used for research, teaching and private study purposes. Any substantial or systematic reproduction, re-distribution, re-selling, loan or sub-licensing, systematic supply or distribution in any form to anyone is expressly forbidden. The publisher does not give any warranty express or implied or make any representation that the contents will be complete or accurate or up to date. -

Diplomatic List
MINISTRY OF FOREIGN AFFAIRS OF THE REPUBLIC OF AZERBAIJAN STATE PROTOCOL DEPARTMENT DIPLOMATIC LIST BAKU July 2021 CONTENTS E m b a s s i e s Afghanistan ................................................................................... 14 Albania .......................................................................................... 15 Algeria .......................................................................................... 16 Angola ........................................................................................... 17 Argentina ...................................................................................... 18 Australia ........................................................................................ 19 Austria ........................................................................................... 20 Bahrain .......................................................................................... 22 Bangladesh .................................................................................... 23 Barbados ....................................................................................... 24 Belarus .......................................................................................... 25 Belgium ......................................................................................... 26 Benin ............................................................................................. 27 Bosnia and Herzegovina ............................................................... 28 Brazil ............................................................................................ -
List of RTI Nodal Officer
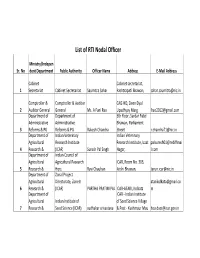
List of RTI Nodal Officer Ministry/Indepen Sr. No dent Department Public Authority Officer Name Address E-Mail Address Cabinet Cabinet secretariat, 1 Secretariat Cabinet Secretariat Saumitra Sahar Rashtrapati Bhawan, [email protected] Comptroller & Comptroller & Auditor CAG HQ, Deen Dyal 2 Auditor General General Ms. A Fani Rao Upadhyay Marg [email protected] Department of Department of 5th Floor, Sardar Patel Administrative Administrative Bhawan, Parliament 3 Reforms & PG Reforms & PG Rakesh Chandra Street [email protected] Department of Indian Veterinary Indian Veterinary Agricultural Research Institute Research Institute, Izzat palsuresh01@rediffmai 4 Research & (ICAR) Suresh Pal Singh Nagar, l.com Department of Indian Council of Agricultural Agricultural Research ICAR, Room No. 303, 5 Research & Hqrs. Ravi Chauhan Krishi Bhawan, [email protected] Department of Zonal Project Agricultural Directorate, Zone II [email protected] 6 Research & (ICAR) PARTHA PRATIM PAL ICAR-ATARI, Kolkata m Department of ICAR - Indian Institute Agricultural Indian Institute of of Seed Science Village 7 Research & Seed Science (ICAR) sudhakar srivastava & Post - Kushmaur Mau [email protected] Department of Vivekananda Parvatiya ICAR- Vivekananda Agricultural Krishi Anusandhan Parvatiya Krishi 8 Research & Sansthan (ICAR) Radhika Arya Anusandhan Sansthan, [email protected] Department of Central Institute for Agricultural Research on Buffalloes rksharmascientist@gm 9 Research & (ICAR) Dr RK Sharma APR Division, ICAR-CIRB ail.com Department -

Doing Business in Azerbaijan2018
DOING BUSINESS IN AZERBAIJAN 2018 AZPROMO established by: MINISTRY OF ECONOMY OF THE REPUBLIC OF AZERBAIJAN 84 U.Hajibayov str., “The Government House”, Baku, Azerbaijan, AZ1000 phone: +994 12 493 88 67 fax: +994 12 492 58 95 e-mail: [email protected] www.economy.gov.az This publication prepared by: AZERBAIJAN EXPORT & INVESTMENT PROMOTION FOUNDATION Baku Business Center, 32 Neftchiler ave., Baku, Azerbaijan, AZ1000 ov phone: +994 12 598 01 47, +994 12 598 01 48 asad fax: +994 12 598 01 52 vasif by e-mail: [email protected] gned i www.azpromo.az des www.export.az DOING BUSINESS IN AZERBAIJAN2018 Important notice: This information is provided for general guidance only. Specific legal advice should be sought prior to taking any action in respect of the matters discussed herein. Every possible effort has been made to ensure that the information con- tained in this book is accurate at the time going to press. Statistical data by: The State Statistical Commit- tee of the Republic of Azerbaijan DOING BUSINESS IN AZERBAIJAN 2018 CONTENTS COUNTRY INFORMATION 9 HISTORY, GEOGRAPHY AND STATE .................................................. 10 ECONOMIC SNAPSHOT ................................................................... 14 WHY AZERBAIJAN 23 POLITICAL AND ECONOMIC STABILITY ............................................ 24 REFORMIST BUSINESS ENVIRONMENT ............................................. 24 ATTRACTIVE INVESTMENT CLIMATE ................................................ 24 SKILLED LABOUR FORCE ................................................................