(2021) Silicon Crystals for Steering High-Intensity Particle Beams At
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
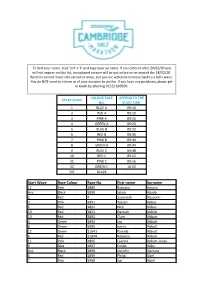
Start Wave Race Colour Race No. First Name Surname
To find your name, click 'ctrl' + 'F' and type your surname. If you entered after 20/02/20 you will not appear on this list, an updated version will be put online on or around the 28/02/20. Runners cannot move into an earlier wave, but you are welcome to move back to a later wave. You do NOT need to inform us of your decision to do this. If you have any problems, please get in touch by phoning 01522 699950. COLOUR RACE APPROX TO THE START WAVE NO. START TIME 1 BLUE A 09:10 2 RED A 09:10 3 PINK A 09:15 4 GREEN A 09:20 5 BLUE B 09:32 6 RED B 09:36 7 PINK B 09:40 8 GREEN B 09:44 9 BLUE C 09:48 10 RED C 09:52 11 PINK C 09:56 12 GREEN C 10:00 VIP BLACK Start Wave Race Colour Race No. First name Surname 11 Pink 1889 Rebecca Aarons Any Black 1890 Jakob Abada 2 Red 4 Susannah Abayomi 3 Pink 1891 Yassen Abbas 6 Red 1892 Nick Abbey 10 Red 1823 Hannah Abblitt 10 Red 1893 Clare Abbott 4 Green 1894 Jon Abbott 8 Green 1895 Jonny Abbott 12 Green 11043 Pamela Abbott 6 Red 11044 Rebecca Abbott 11 Pink 1896 Leanne Abbott-Jones 9 Blue 1897 Emilie Abby Any Black 1898 Jennifer Abecina 6 Red 1899 Philip Abel 7 Pink 1900 Jon Abell 10 Red 600 Kirsty Aberdein 6 Red 11045 Andrew Abery Any Black 1901 Erwann ABIVEN 11 Pink 1902 marie joan ablat 8 Green 1903 Teresa Ablewhite 9 Blue 1904 Ahid Abood 6 Red 1905 Alvin Abraham 9 Blue 1906 Deborah Abraham 6 Red 1907 Sophie Abraham 1 Blue 11046 Mitchell Abrams 4 Green 1908 David Abreu 11 Pink 11047 Kathleen Abuda 10 Red 11048 Annalisa Accascina 4 Green 1909 Luis Acedo 10 Red 11049 Vikas Acharya 11 Pink 11050 Catriona Ackermann -

Year in Review Overtime Goal Propels Water Polo to Fifth Straight State Title
Volume LXXXIII, Issue XXIX St. Louis University High School | Friday, May 17, 2019 sluh.org/prepnews Conversation Overtime goal propels water polo to fifth Renos for Carruthers straight State title next year reflects on begin this first year summer at SLUH BY Nicholas Dalaviras and Sam Tarter STAFF Editors’ Note: On Tuesday, PN 83 Editor in Chief Paul Gillam and PN 84 Editor in s the 2018-2019 school Chief Johno Jackson sat down Ayear comes to a close, with SLUH President Alan the St. Louis U. High main- Carruthers to discuss his first tenance staff’s remodeling year at SLUH. The following plans are just beginning to transcription has been edited take shape. From working on for length. big projects, like renovating the third floor of the Science Paul Gillam: So for you, this Wing, to smaller touch-ups, year has been full of transi- like painting and replacing tions. You’ve moved schools carpeting, the maintenance you’ve worked at. You’ve crew will have its hands full moved states. You became a all summer to help the school president, and you hopefully look its best. have made it through them Work will begin af- unscathed. How do you feel? ter Memorial Day weekend on May 28, and continue Alan Carruthers: You know, throughout the summer. I feel pretty good actually this Demolition and reno- time of year. I feel last night vation of the upper science I was able to get to the base- Mr. Dan Schulte and junior Jordan Smith after the water polo State Championship. -

Surname First Name Categorisation Abadin Jose Luis Silver Abbelen
2018 DRIVERS' CATEGORISATION LIST Updated on 09/07/2018 Drivers in red : revised categorisation Drivers in blue : new categorisation Surname First name Categorisation Abadin Jose Luis Silver Abbelen Klaus Bronze Abbott Hunter Silver Abbott James Silver Abe Kenji Bronze Abelli Julien Silver Abergel Gabriele Bronze Abkhazava Shota Bronze Abra Richard Silver Abreu Attila Gold Abril Vincent Gold Abt Christian Silver Abt Daniel Gold Accary Thomas Silver Acosta Hinojosa Julio Sebastian Silver Adam Jonathan Platinum Adams Rudi Bronze Adorf Dirk Silver Aeberhard Juerg Silver Afanasiev Sergei Silver Agostini Riccardo Gold Aguas Rui Gold Ahlin-Kottulinsky Mikaela Silver Ahrabian Darius Bronze Ajlani Karim Bronze Akata Emin Bronze Aksenov Stanislas Silver Al Faisal Abdulaziz Silver Al Harthy Ahmad Silver Al Masaood Humaid Bronze Al Qubaisi Khaled Bronze Al-Azhari Karim Bronze Alberico Neil Silver Albers Christijan Platinum Albert Michael Silver Albuquerque Filipe Platinum Alder Brian Silver Aleshin Mikhail Platinum Alesi Giuliano Silver Alessi Diego Silver Alexander Iradj Silver Alfaisal Saud Bronze Alguersuari Jaime Platinum Allegretta Vincent Silver Alleman Cyndie Silver Allemann Daniel Bronze Allen James Silver Allgàuer Egon Bronze Allison Austin Bronze Allmendinger AJ Gold Allos Manhal Bronze Almehairi Saeed Silver Almond Michael Silver Almudhaf Khaled Bronze Alon Robert Silver Alonso Fernando Platinum Altenburg Jeff Bronze Altevogt Peter Bronze Al-Thani Abdulrahman Silver Altoè Giacomo Silver Aluko Kolawole Bronze Alvarez Juan Cruz Silver Alzen -

SP 2020 Degrees Conferred
THE OHIO STATE UNIVERSITY Degrees Conferred SPRING SEMESTER 2020 Data as of June 10, 2020 Alabama Sorted by Zip Code, City and Last Name Degree Student Name (Last, First, Middle) City State Zip Degree Honor Gee, Kristina Vestavia Hills AL 35216 Bachelor of Science Cum Laude Harmon, Kassidie Serae Madison AL 35756 Bachelor of Science w/Rsrch Distnctn in Psychology Madison AL 35756 Bachelor of Science Magna Cum Laude Blake, Shanterica Micyoun Irvington AL 36544 Master of Arts THE OHIO STATE UNIVERSITY OSAS - Analysis and Reporting June 10, 2020 Page 1 of 158 THE OHIO STATE UNIVERSITY Degrees Conferred SPRING SEMESTER 2020 Data as of June 10, 2020 Alaska Sorted by Zip Code, City and Last Name Degree Student Name (Last, First, Middle) City State Zip Degree Honor Liu, David Anchorage AK 99515 Bachelor of Science Cum Laude Foudeas, Penelope Anchorage AK 99516 Bachelor of Science THE OHIO STATE UNIVERSITY OSAS - Analysis and Reporting June 10, 2020 Page 2 of 158 THE OHIO STATE UNIVERSITY Degrees Conferred SPRING SEMESTER 2020 Data as of June 10, 2020 Arizona Sorted by Zip Code, City and Last Name Degree Student Name (Last, First, Middle) City State Zip Degree Honor Carboun, Kaitlyn Brooke Mesa AZ 85207 Bachelor of Science Cum Laude Gauthier, LeeAnn Mesa AZ 85208 Master of Social Work Cunningham, Caitlin Marie Chandler AZ 85225 Doctor of Veterinary Medicine Stanfield, Christian P Chandler AZ 85249 Doctor of Dental Surgery Wright, Renae JeeAnn Scottsdale AZ 85250 Doctor of Nursing Practice Welch, Ryan James Scottsdale AZ 85254 Bachelor of Science -

PETITION List 04-30-13 Columns
PETITION TO FREE LYNNE STEWART: SAVE HER LIFE – RELEASE HER NOW! • 1 Signatories as of 04/30/13 Arian A., Brooklyn, New York Ilana Abramovitch, Brooklyn, New York Clare A., Redondo Beach, California Alexis Abrams, Los Angeles, California K. A., Mexico Danielle Abrams, Ann Arbor, Michigan Kassim S. A., Malaysia Danielle Abrams, Brooklyn, New York N. A., Philadelphia, Pennsylvania Geoffrey Abrams, New York, New York Tristan A., Fort Mill, South Carolina Nicholas Abramson, Shady, New York Cory a'Ghobhainn, Los Angeles, California Elizabeth Abrantes, Cambridge, Canada Tajwar Aamir, Lawrenceville, New Jersey Alberto P. Abreus, Cliffside Park, New Jersey Rashid Abass, Malabar, Port Elizabeth, South Salma Abu Ayyash, Boston, Massachusetts Africa Cheryle Abul-Husn, Crown Point, Indiana Jamshed Abbas, Vancouver, Canada Fadia Abulhajj, Minneapolis, Minnesota Mansoor Abbas, Southington, Connecticut Janne Abullarade, Seattle, Washington Andrew Abbey, Pleasanton, California Maher Abunamous, North Bergen, New Jersey Andrea Abbott, Oceanport, New Jersey Meredith Aby, Minneapolis, Minnesota Laura Abbott, Woodstock, New York Alexander Ace, New York, New York Asad Abdallah, Houston, Texas Leela Acharya, Toronto, Canada Samiha Abdeldjebar, Corsham, United Kingdom Dennis Acker, Los Angeles, California Mohammad Abdelhadi, North Bergen, New Jersey Judith Ackerman, New York, New York Abdifatah Abdi, Minneapolis, Minnesota Marilyn Ackerman, Brooklyn, New York Hamdiya Fatimah Abdul-Aleem, Charlotte, North Eddie Acosta, Silver Spring, Maryland Carolina Maria Acosta, -

2018 Poets House Showcase
Poets House | 10 River Terrace | New York, NY 10282 | poetshouse.org ELCOME to the 2018 Poets House Showcase, our annual, all-inclusive exhibition of the most recent poetry books, chapbooks, broadsides, artist’s books, and multimedia works published in the United States and abroad. W This year marks the 26th anniversary of the Poets House Showcase and features over 3,400 books from more than 750 different presses and publishers. For 26 years, the Showcase has helped to keep our collection current and relevant, building one of the most extensive collections of poetry in our nation—an expansive record of the poetry of our time, freely available and open to all. Every year, Poets House invites poets and publishers to participate in the annual Showcase by donating copies of poetry titles released since January of the previous year. This year’s exhibit highlights poetry titles published in 2017 and the first part of 2018. Books have been contributed by the entire poetry community, from the poets and publishers who send on their newest titles as they’re released, to library visitors donating books when they visit us. Every newly published book is welcomed, appreciated, and featured in the Showcase. Poets House provides a comprehensive, inclusive collection of poetry that is free and open to the public. The Poets House Showcase is the mechanism through which we build our collection, and to make it as comprehensive as possible, the library staff reaches out to as many poetry communities and producers as we can. To meet the different needs of our many library patrons, we aim to bring together poetic voices of all kinds. -

Avon Cemeteries Photo Survey, 2005.Xlsx
Town Cemetery Photo # First Name(s) Last Name Dates Notes Avon Avon 0009 Richard Kelly (Sr.) Frew Avon Avon 0010 Michael S. Frew Avon Avon 0011 Jeffrey S. Frew Avon Avon 0012 Geoffrey K. Schantz Avon Avon 0013 Edwin A. Noyes Avon Avon 0013 Vera V. Noyes Avon Avon 0014 Bessie S. Northrup Avon Avon 0015 Arthur S. Northrup Avon Avon 0016 Bessie I. Northrup Avon Avon 0017 Lewis A. Orman Avon Avon 0017 Ada A. Orman Avon Avon 0018 Karolina P. Putnam Avon Avon 0018 Clair H. Putnam Avon Avon 0019 Randy B. Kelley Avon Avon 0020 Tammy Thompson Avon Avon 0021 Fred J. Roggenbaum Avon Avon 0021 Mary S. Roggenbaum Avon Avon 0022 Arliene Rice Whisker Avon Avon 0023 Maurice E. Whisker Avon Avon 0024 Velma Roberts Whisker Avon Avon 0025 Daniel P. (Sr.) Bookhart Avon Avon 0025 Elouise O. Bookhart Avon Avon 0026 Howard R. Bailey Avon Avon 0026 Florence Orman Bailey Avon Avon 0027 Emma J. Tutchell Avon Avon 0028 Anna M. Tutchell Avon Avon 0029 Mary Rowan Legg Avon Avon 0030 John M. Legg Avon Avon 0031 Ernest W. Northrup Avon Avon 0031 Mary H. Northrup Avon Avon 0032 Samuel Northrup middle initial I. or L. Avon Avon 0033 Mable C. Van Cleft Avon Avon 0034 Nettie Moynes Eggleston Avon Avon 0035 Charles H. Eggleston Avon Avon 0036 Martha Ann Eggleston Iler Avon Avon 0038 Jerusha Benedict Town Cemetery Photo # First Name(s) Last Name Dates Notes Avon Avon 0039 Jason B. Benedict Avon Avon 0040 Sarah A. Benedict Avon Avon 0043 J. F. (Jr.) E. -

Undergraduate.Pdf
Commencement 2020 t UNDERGRADUATE STUDENT EDITION 1 Commencement 2020 t CONTENTS 3 Message from the University President 4 College of Community and Public Affairs 8 Decker College of Nursing and Health Sciences 13 Harpur College of Arts and Sciences 30 School of Management 36 Thomas J. Watson School of Engineering and Applied Science 43 Honors and Special Programs 60 About Binghamton University 63 Trustees, Council and Administration 2 MESSAGE FROM THE UNIVERSITY PRESIDENT MESSAGE FROM THE UNIVERSITY PRESIDENT raduates, parents and friends: Commencement is always the highlight of the academic year, for the students we are honoring, especially, but also for the faculty and staff who have Ghelped our students achieve so much. When the COVID-19 pandemic abruptly changed our lives this spring, sending students home and curtailing so many of the activities we all would have experienced had they remained on campus, most painful was the postponement of the University’s Commencement exercises that are traditionally the highlight of the academic year. Our graduates have gained the experiences and knowledge that their careers and future engagements will demand of them. Ours is a campus where students learn by doing, and our graduates have already proven themselves — winning prestigious case competitions and grants, publishing papers that have gained acclaim from scientists and scholars, and bettering their communities through hands-on internships and practicums. Outside the classroom, they have embraced their responsibilities as active members of the community. They’ve raised funds to combat deadly disease, provided food for the hungry, taught younger students in local schools and traveled across the globe to work with and learn from their international peers. -

Cayuga County Surname and Family Files in Town and Organization Collections
Cayuga County Surname and Family Files In town and organization collections A B C D E F G 1 Surname Cayuga County Genoa Moravia Town of Town of Montezuma 2 x = family name on file Historian Hist. Assn. COLHS Sterling Victory Hist. Society 3 4 Moravia names also online @ www.colhs.org/p/surnames see 5 Montezuma names online @ www.montezumagen.com website 6 7 Abbe x 8 Abbott x x x x 9 Abbott-Nuitt x 10 Abraham(s) x 11 Abrams x x x 12 Acers x 13 Acker x 14 Ackerman x x 15 Ackerson x x x 16 Ackles x 17 Ackley x 18 Acre x 19 Adams x x x x 20 Adams-Crofoot x 21 Addy x 22 Adessa x 23 Adkins x 24 Adle x 25 Adolph x 26 Adriance x x 27 Adsitt x 28 Agree x 29 Aiken/Aikin x 30 Aikin x 31 Akin x 32 Akin (Aiken) x 33 Albertson x 34 Albie/Albee x 35 Albring x 36 Albro x 37 Alcorn x 38 Alcott/Alcox x 39 Alden x 40 Aldrich x x 41 Aldridge x 42 Alexander x x 43 Alfred x 44 Alger/Algur x 45 Algert x 46 Alifieri x 47 Alissandrello x 48 Allanson x 49 Allee x 50 Allen x x x x x 51 Alley x 52 Allis x 53 Almy x 54 Alnutt x x Cayuga County Surname and Family Files In town and organization collections A B C D E F G 1 Surname Cayuga County Genoa Moravia Town of Town of Montezuma 2 x = family name on file Historian Hist. -

Section C, Part I1 ITALIAN SURNAMES
Section C, Part I1 ITALIAN SURNAMES INTRODUCTION Three naming customs derived from early Greek settlers, the Roman republics, and the invading Germanic tribes. Greek: Adding theiname of the father plus the name of the family or tribe to the given name. Roman: Adding the name of the family clan to the given name. Germanic tribes: Attaching an ancestor's name with a similar beginning sound to the given name: Pompeo Pomponio, Alberto d9Alberto, and Garibald FaroaM or Garibald Romuald. PATRONYMICS One of the oldest and most wide-spread expressions of paternity used in Italy is characterized by the preposition di (of), entered between two given names; for example, Pietro di Giovanni (Peter the son of John). With each new generation, the combination of names increased; hence Pietro's .son Leonardo would be known as Leonardo di Fietro di Giovanni. Eventually a hereditary name was standardized, but the Italian records from which you will be extracting data continues a variation of this practice that can be confusing. A large segment of Italian names today contain the preposition di between the given name and surname: di Paolu, d7Albe&o. Sometimes the records also contain individuals' names the names of the father and even the grandfather inserted between the given name and surname: Francesco di Giovanni d9Angelo is actually Francesco (the son of Giovanni) d'Angelo. There is a general rule for extracting Italian names that holds true in most instances: Omit given names beDgiming with di. To be certain, it is a wise practice to compare the apparent inserted name with the name of the father and grandfather if they are gven elsewhere in the record. -

Naturalization Index (1904-1958)
Naturalization Index (1904-1958) SURNAME FIRST NAMEMid Name VOL PAGE ADDRESS DATE ERTIFICATE MEMO Abbots William Lovatt 2 13 Buffington Twp 22-Feb-04 Auden Albert 2 47 Glen Campbell 19-Mar-04 Auden Alfred 2 81 Glen Campbell 19-Mar-04 Arur Pul 2 93 Glen Campbell 19-Mar-04 Alik Frank 2 109 Glen Campbell 28-Mar-04 Elik Anderson Andrew 2 149 Ernest 06-Oct-04 Areco Nicholas 2 175 Rossiter 18-Feb-06 Azzara Gaetano 1 7 Clymer 20-Aug-07 13972 Anderson Alfred 2A 16 Dixonville 16-Aug-10 46093 Adamson Charles 2A 33 Wehrum Denied (Later admitted) Adamson Charles 2A 45 Wehrum 27-Aug-11 192257 Adelburg Harry 2A 60 Iselin 13-Feb-12 236264 Alexander, John 2A 71 Dixonville 13-Feb-12 236268 Anderson Alex 3 12 Iselin 11-Feb-13 302444 Augustine Frank 3 98 Glen Campbell 19-Aug-13 406492 Adams John 4 5 Tunnelton 19-Aug-13 359826 Astalos John 4 35 Saltsburg 10-Feb-14 460511 Artzmowicz Frank 4 64 Clymer 18-Aug-14 460544 Andrasain Joseph 4 87 Saxman 09-Feb-15 516121 Anderson Abbonizio Consiglio 5 55 Tunnelton 04-Aug-15 501713 Abruzzi Massimo 5 100 Tunnelton Cancelled Alaimo Angelo 6 26 Chambersville 02-Feb-16 504783 Alimo Adair Hans, Jr. 6 67 Ernest 02-Aug-16 731877 Amantea Antonio 6 72 Heilwood 02-Aug-16 731872 Amerando Leonardo 7 2 McIntyre 15-Feb-17 735426 Abraham John 7 20 Clymer Spoiled petition Allesandro Vito 7 72 Chambersville 01-Aug-17 737682 Antonucci Donato 7 74 Strangford Denied Adamcik Imrich 8 24 Blairsville 05-May-20 1330954 Annunis Matt 8 43 Ernest 07-Feb-18 828258 Arvins Arvins Matt 8 43 Ernest 07-Feb-18 828258 Annunis Acciaccaferro Francesco -

Final Entries - Athletes List by Event European Athletics U23 Championships 2021, Tallinn (EST)
Final Entries - Athletes List by event European Athletics U23 Championships 2021, Tallinn (EST) Tot. Number of countries Tot. Number of athletes Tot. Number of Men Tot. Number of Women 48 1180 600 580 FINAL ENTRIES 100 Metres Under 23 Men Num. of countries: 15 Num. of athletes: 22 Member Federation Surname First Name DoB PB SB CZE HAMPL Štěpán 10/11/1999 10.35 10.35 DEN KJÆR Emil Mader 20/12/1999 10.44 10.44 ESP LÓPEZ Sergio 05/07/1999 10.36 10.36 ESP MONNE Arnau 10/08/2000 10.31 10.31 ESP MONTALVO Pablo 20/10/1999 10.34 10.34 EST NAZAROV Karl Erik 17/03/1999 10.42 10.42 EST SAI Henri 04/12/2000 10.43 10.43 FIN ILLUKKA Riku 21/09/1999 10.27 10.27 GBR ASHWELL Dominic 13/06/1999 10.20 10.34 GBR AZU Jeremiah 15/05/2001 10.27 10.38 GBR MINGELI Brandon 07/09/2000 10.29 10.29 GER HARTMANN Joshua 09/06/1999 10.14 10.30 GER WOLF Yannick 12/05/2000 10.27 10.32 ITA CECCARELLI Samuele 09/01/2000 10.45 10.45 LAT ZĀLĪTIS Roberts Jānis 14/09/2000 10.46 10.46 POR PRAZERES André 23/05/1999 10.50 10.50 SMR SANSOVINI Francesco 18/01/2000 10.68 10.68 SUI LESTRADE Bradley 22/04/2001 10.48 10.48 SWE LARSSON Henrik 30/09/1999 10.20 10.29 TUR YILDIRIM Furkan 06/03/1999 10.49 10.60 UKR KOSTRYTSYA Erik 18/09/1999 10.36 10.36 UKR VASYLIEV Andrii 13/04/2001 10.47 10.47 28 Jun 2021 18:29 CEST Page 1 of 52 Final Entries - Athletes List by event European Athletics U23 Championships 2021, Tallinn (EST) FINAL ENTRIES 200 Metres Under 23 Men Num.