Equilibrium Analyses of the Recovery Feasibility of Four Atlantic Salmon (Salmo Salar) Populations in Nova Scotia and Southwest New Brunswick
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Program and Abstracts.Docx
The 2020 Atlantic Salmon Ecosystems Forum Time flies – Atlantic salmon as an endangered species twenty years later… January 14-15, 2020 Orono, Maine USA University of Maine, Wells Conference Center Recognizing the International Year of the Salmon (focus) in 2019, watch for activities extending into 2020 2020 Atlantic Salmon Ecosystems Forum Schedule At A Glance Begin End January 14, 2020 7:00 8:00 REGISTRATION - Refreshments provided 8:00 8:05 Housekeeping Rory Saunders, NOAA Fisheries 8:05 8:25 Welcome to the 2020 ASEF Sam Rauch, Deputy Assistant Administrator for Regulatory Programs, NOAA Fisheries 8:25 9:00 Sustainability as a framework for rethinking approaches to salmon, society and solutions. David Hart, Director, Senator George J. Mitchell Center for Sustainability Solutions 9:00 9:05 Session I: 20 Years of Experience Guiding our Future (Part 1 of 2) Joshua Royte, The Nature Conservancy, Moderator 9:05 9:25 Reflections on Penobscot River Atlantic Salmon: Before and After Listing as an Endangered Species Edward T Baum, Maine Atlantic Sea-Run Salmon Commission (Retired) 9:25 9:45 From North America to West Greenland and Beyond: management of Atlantic salmon in the North Atlantic Martha Jean Robertson, Fisheries and Oceans Canada, Newfoundland and Labrador, Canada 9:45 10:15 BREAK - refreshments provided 10:15 10:25 Science for comfort or conservation- how do we inform and avoid action on fish passage? Joseph D Zydlewski, U.S. Geological Survey, Maine Cooperative Fish and Wildlife Research 10:25 10:35 Using decision support tools to plan for salmon restoration Erik H Martin, The Nature Conservancy 10:35 10:45 6 ½ & 19 years Maintaining and Perfecting SHARE’s Mission Focus Steven D. -
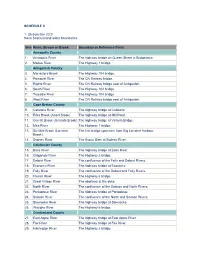
Nova Scotia Inland Water Boundaries Item River, Stream Or Brook
SCHEDULE II 1. (Subsection 2(1)) Nova Scotia inland water boundaries Item River, Stream or Brook Boundary or Reference Point Annapolis County 1. Annapolis River The highway bridge on Queen Street in Bridgetown. 2. Moose River The Highway 1 bridge. Antigonish County 3. Monastery Brook The Highway 104 bridge. 4. Pomquet River The CN Railway bridge. 5. Rights River The CN Railway bridge east of Antigonish. 6. South River The Highway 104 bridge. 7. Tracadie River The Highway 104 bridge. 8. West River The CN Railway bridge east of Antigonish. Cape Breton County 9. Catalone River The highway bridge at Catalone. 10. Fifes Brook (Aconi Brook) The highway bridge at Mill Pond. 11. Gerratt Brook (Gerards Brook) The highway bridge at Victoria Bridge. 12. Mira River The Highway 1 bridge. 13. Six Mile Brook (Lorraine The first bridge upstream from Big Lorraine Harbour. Brook) 14. Sydney River The Sysco Dam at Sydney River. Colchester County 15. Bass River The highway bridge at Bass River. 16. Chiganois River The Highway 2 bridge. 17. Debert River The confluence of the Folly and Debert Rivers. 18. Economy River The highway bridge at Economy. 19. Folly River The confluence of the Debert and Folly Rivers. 20. French River The Highway 6 bridge. 21. Great Village River The aboiteau at the dyke. 22. North River The confluence of the Salmon and North Rivers. 23. Portapique River The highway bridge at Portapique. 24. Salmon River The confluence of the North and Salmon Rivers. 25. Stewiacke River The highway bridge at Stewiacke. 26. Waughs River The Highway 6 bridge. -

Ices Wgnas 2012 Addendum
ICES WGNAS 2012 ADDENDUM ICES Advisory Committee ICES CM 2012/ACOM:09 ICES COMPILATION OF MICROTAGS, FINCLIP AND EXTERNAL TAG RELEASES 2011 BY THE WORKING GROUP ON NORTH ATLANTIC SALMON 26 MARCH–4 APRIL 2012 COPENHAGEN, DENMARK International Council for the Exploration of the Sea Conseil International pour l’Exploration de la Mer H. C. Andersens Boulevard 44–46 DK-1553 Copenhagen V Denmark Telephone (+45) 33 38 67 00 Telefax (+45) 33 93 42 15 www.ices.dk [email protected] Recommended format for purposes of citation: ICES. 2012. ICES Compilation of Microtags, Finclip and External Tag Releases 2011 by the Working Group on North Atlantic Salmon. ICES WGNAS 2012 ADDENDUM 26 March–4 April 2012. 31 pp. For permission to reproduce material from this publication, please apply to the General Secretary. This document is a report of an Expert Group under the auspices of the International Council for the Exploration of the Sea and does not necessarily represent the view of the Council. © 2012 International Council for the Exploration of the Sea ICES WGNAS 2012 ADDENDUM | i Contents 1 Terms of Reference ........................................................................................................ 2 2 Summary table ............................................................................................................... 3 3 Number of tags and marks applied to Atlantic salmon by country for 2011 ................................................................................................................................... 5 3.1 Canada .................................................................................................................. -

South Western Nova Scotia
Netukulimk of Aquatic Natural Life “The N.C.N.S. Netukulimkewe’l Commission is the Natural Life Management Authority for the Large Community of Mi’kmaq /Aboriginal Peoples who continue to reside on Traditional Mi’Kmaq Territory in Nova Scotia undisplaced to Indian Act Reserves” P.O. Box 1320, Truro, N.S., B2N 5N2 Tel: 902-895-7050 Toll Free: 1-877-565-1752 2 Netukulimk of Aquatic Natural Life N.C.N.S. Netukulimkewe’l Commission Table of Contents: Page(s) The 1986 Proclamation by our late Mi’kmaq Grand Chief 4 The 1994 Commendation to all A.T.R.A. Netukli’tite’wk (Harvesters) 5 A Message From the N.C.N.S. Netukulimkewe’l Commission 6 Our Collective Rights Proclamation 7 A.T.R.A. Netukli’tite’wk (Harvester) Duties and Responsibilities 8-12 SCHEDULE I Responsible Netukulimkewe’l (Harvesting) Methods and Equipment 16 Dangers of Illegal Harvesting- Enjoy Safe Shellfish 17-19 Anglers Guide to Fishes Of Nova Scotia 20-21 SCHEDULE II Specific Species Exceptions 22 Mntmu’k, Saqskale’s, E’s and Nkata’laq (Oysters, Scallops, Clams and Mussels) 22 Maqtewe’kji’ka’w (Small Mouth Black Bass) 23 Elapaqnte’mat Ji’ka’w (Striped Bass) 24 Atoqwa’su (Trout), all types 25 Landlocked Plamu (Landlocked Salmon) 26 WenjiWape’k Mime’j (Atlantic Whitefish) 26 Lake Whitefish 26 Jakej (Lobster) 27 Other Species 33 Atlantic Plamu (Salmon) 34 Atlantic Plamu (Salmon) Netukulimk (Harvest) Zones, Seasons and Recommended Netukulimk (Harvest) Amounts: 55 SCHEDULE III Winter Lake Netukulimkewe’l (Harvesting) 56-62 Fishing and Water Safety 63 Protecting Our Community’s Aboriginal and Treaty Rights-Community 66-70 Dispositions and Appeals Regional Netukulimkewe’l Advisory Councils (R.N.A.C.’s) 74-75 Description of the 2018 N.C.N.S. -

The Geographic Distribution and Aspects of the Parasite/Host
Geographic distribution and aspects of the parasite/host relationships of the invasive swim bladder parasite Anguillicoloides crassus infecting American eel (Anguilla rostrata) in mainland Nova Scotia and New Brunswick By Dollie M. Campbell A Thesis submitted to Saint Mary’s University, Halifax, Nova Scotia in Partial Fulfillment of the Requirements for the Degree of Master of Science in Applied Science April 2014, Halifax, Nova Scotia © Dollie M. Campbell 2014 Approved: Dr. David Cone Supervisor Approved: Dr. David Cairns External examiner Approved: Dr. Katherine Jones Committee member Approved: Dr. Ron Russell Committee member Approved: Dr. Susan Bjornson Graduate Studies Rep. Date: April 15, 2014 Table of Contents ABSTRACT iii ACKNOWLEDGEMENTS iv LIST OF TABLES v LIST OF FIGURES vi - ix INTRODUCTION 1 - 7 MATERIALS AND METHODS Eel collection 7 - 9 Eel necropsies 9 - 10 Data analysis 10 - 11 RESULTS 11 - 13 Parasite host relationship and diet 12 - 13 DISCUSSION 14 - 19 REFERANCES 20 - 26 APPENDIX 1. 0 : American eel otolith preparation and ageing 62 - 66 ii Abstract Geographic distribution and aspects of the parasite/host relationships of the invasive swim bladder parasite Anguillicoloides crassus infecting American eel (Anguilla rostrata) in mainland Nova Scotia and New Brunswick Dollie M. Campbell Between 2008-2013, 1,981 eels were collected from 174 localities throughout mainland Nova Scotia and New Brunswick and necropsied for the swim bladder nematode Anguillicoloides crassus. Overall prevalence of A. crassus was 4 % with a mean intensity of 3.8 ± 8 SD (1-63 parasites). The Southern Uplands, Gulf of St. Lawrence and the Bay of Fundy regions were all identified as having rivers with eels infected with the nematode. -

Summary of Fish Tagging Maritimes Region 1967-1975
,rY -FX/i/-fi-i(Z) -4)A'Sf/ C, Canada. Fisheries and Marine + Environment Canada Environnement Canada Service. Maritimes Region. Fisheries and Service des peches Resource Development Branch. Marine Service et des sciences de tamer DATA RECORD SERIES MAR/D Summary of Fish Tagging Maritimes Region 1967-1975 '1 Ct by id Karen Newbould 4,0-E Ravi94- )4-4 Data Record Series No. MAR/ D-76-1 IviAv 7 1976 DFPT. OF THE Cf41VCROt riMEP141.■ Resource Development Branch FISHER'IES SERVICE ra. s. Maritimes Region SUMMARY OF FISH TAGGING MARITIMES REGION (1967-1975) KAREN NEWBOULD MARCH, 1976 DATA RECORD SERIES NO. MAR/D-76-1 RESOURCE DEVELOPMENT BRANCH FISHERIES AND MARINE SERVICE DEPARTMENT OF THE ENVIRONMENT HALIFAX, NOVA SCOTIA 111 CONTENTS EXPLANATION OF SHORT FORMS USED FOR TAG TYPE INTRODUCTION ATLANTIC SALMON - ADULTS NOVA SCOTIA Medway River 3 East River, Sheet Harbour 4 Shubenacadie River System 6 Great Village River 7 St. Mary's River 8 River Philip 9 St. Margaret's Bay 10 NEW BRUNSWICK Saint John River System 11 Saint John Harbour and Westfield 11 Bay of Fundy 13 Below Mactaquac 14 Mactaquac Headpond 15 Mactaquac Migration Channel 15 Upriver Transfers from Mactaquac 17 Nashwaak River 23 Tobique River 25 Miramichi River System 26 Petiticodiac River System 32 Big Salmon River 33 Counting Fence 33 Bay of Fundy 33 St. Croix River 34 Restigouche River 35 ATLANTIC SALMON - JUVENILES NOVA SCOTIA River Philip System 37 Margaree River System 39 Medway River System 42 LaHave River System 43 Shubenacadie River System 47 East and West River Sheet Harbour System 49 iv NOVA SCOTIA (continued) St. -

C S a S S C C S
C S A S S C C S Canadian Science Advisory Secretariat Secrétariat canadien de consultation scientifique Proceedings Series 2004/046 Série des comptes rendus 2004/046 Mitigation for Acid Rain Impacts on Atténuation des effets des pluies Atlantic Salmon and Their Habitat acides sur le saumon atlantique et son habitat 19-20 April 2004 Les 19 et 20 avril 2004 Atlantic Salmon Federation Centre de conférences de la Conference Center Fédération du saumon atlantique Chamcook, New Brunswick Chamcook, Nouveau-Brunswick T.L. Marshall1 (Chair), D. Kircheis2 T.L. Marshall1 (Chair), D. Kircheis2 T. Clair3, and K.A. Rutherford1 T. Clair3, and K.A. Rutherford1 1 1 Department of Fisheries and Oceans Ministère des Pêches et des Océans P.O. Box 1006, Dartmouth, N.S. B2Y 4A2 C. P. 1006, Dartmouth (N.-É.) B2Y 4A2 2National Oceanic and Atmospheric 2National Oceanic and Atmospheric Administration (NOAA) Administration (NOAA) 17 Godfrey Drive, Orono, ME 04473 17 Godfrey Drive, Orono, ME 04473 3 Environment Canada 3 Environnement Canada P.O. Box 6227, Sackville, N.B. E4L 1G6 C. P. 6227, Sackville (N.-B.) E4L 1G6 May 2005 / mai 2005 Foreword The purpose of these proceedings is to archive the activities and discussions of the meeting, including research recommendations, uncertainties, and to provide a place to formally archive official minority opinions. As such, interpretations and opinions presented in this report may be factually incorrect or mis-leading, but are included to record as faithfully as possible what transpired at the meeting. No statements are to be taken as reflecting the consensus of the meeting unless they are clearly identified as such. -

APPENDIX I Aboriginal Fishing Licences Information
SCOTIAN BASIN EXPLORATION DRILLING PROJECT – ENVIRONMENTAL IMPACT STATEMENT Appendix I – Aboriginal Fishing Licences Information APPENDIX I Aboriginal Fishing Licences Information Scotia-Fundy Communal Commercial Licences by Aboriginal Organization (2015-2016) Aboriginal Organization Licence Id Species Description Licence Type Description Licence Area Description Licence Subtype Description ACADIA FIRST NATION 300209 ALEWIVES/GASPEREAU CC NON-VESSEL BASED LIMITED TUSKET RIVER ACADIA FIRST NATION 120769 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 120846 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 120981 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 121964 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 122000 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 122046 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 122096 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 4 ACADIA FIRST NATION 122141 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 2 ACADIA FIRST NATION 122184 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 3 ACADIA FIRST NATION 122251 CLAMS, UNSPECIFIED CC NON-VESSEL BASED LIMITED CLAM HARVEST AREA - 4 ACADIA FIRST NATION 338316 CRAB, GREEN CC NON-VESSEL BASED LIMITED ACADIA FIRST NATION 338316 CRAB, GREEN CC NON-VESSEL -

Effects of Partial-Catchment Helicopter Liming on Stream Water Chemistry in West River Sheet Harbour, Nova Scotia
Effects of partial-catchment helicopter liming on stream water chemistry in West River Sheet Harbour, Nova Scotia Lobke Rotteveel Supervisors: Dr. Shannon M. Sterling (Earth Sciences Department, Dalhousie University) Dr. Edmund A. Halfyard (Nova Scotia Salmon Association) Submitted in partial fulfillment of the requirements for the degree of Honours Bachelor of Science at Dalhousie University Halifax, Nova Scotia April 2018 BSc in Environmental Sciences Honour’s Thesis Table of Contents 1 Introduction ............................................................................................................................. 5 1.1 Problem Statement ........................................................................................................... 5 1.2 Background ...................................................................................................................... 6 1.2.1 Freshwater acidification in Nova Scotia ................................................................... 6 1.2.2 Mobilization of aluminium due to acidification ....................................................... 7 1.2.3 Aluminium speciation in acidified waters ................................................................ 7 1.2.4 Effects of chronic freshwater acidification on Atlantic salmon................................ 8 1.2.5 Mitigating freshwater acidification ........................................................................... 9 1.3 Knowledge Gap ............................................................................................................. -

Bedford Institute of Oceanography
BEDFORD INSTITUTE OF OCEANOGRAPHY ANNUAL REVIEW I 2005 Change of address notices, requests for copies, and other correspondence regarding this publication should be sent to: The Editor, BIO 2005 in Review Bedford Institute of Oceanography P.O. Box 1006 Dartmouth, Nova Scotia Canada B2Y 4A2 E-mail address: [email protected] Cover photo: The CCGS Amundsen passes through Lancaster Sound during the ship’s inaugural voyage in August 2003, almost 100 years to the day after Roald Amundsen sailed the same waters during his historic voyage through the Northwest Passage on the Gjoa (1903-1906). © Martin Fortier, ArcticNet NCE Photo is courtesy of Dr. Martin Fortier, who was Chief Scientist on the voyage. Dr. Fortier, of Université Laval, is the Executive Director of ArcticNet, a Network of Centres of Excellence of Canada that brings together scientists and managers in the natural, human health, and social sciences with their partners in Inuit organizations, northern communities, government, and industry to help Canadians face the impacts and opportunities of climate change in the Arctic. Back cover photo: CCGS Amundsen engaged in mapping work in Canada’s Arctic, August 2005 © Jonathan Beaudoin Photo is courtesy of Jonathan Beaudoin, a PhD student at the University of New Brunswick in Fredericton, whose main research interest is the application of oceanographic databases for multibean echosounding in the Canadian Arctic Archipelago. Jonathan, who holds bachelor degrees in Geomatics Engineering and Computer Science, is the Ocean Mapping Group’s dedicated -

Anglers' Handbook • 2018 1 Message from Honourable Keith Colwell, Minister of Fisheries and Aquaculture
ANGLERS’ HANDBOOK and 2018 Summary of Regulations Licence Changes for Free Sportfishing Residents and Weekends Non-Residents June 2–3, 2018 See page 11 for details February 16–18, 2019 Here To Protect Nova Scotia’s Resources Conservation Officers have authority to carry side arms, make arrests, and lay charges. They can also seize vehicles, equipment, weapons, and illegal fish & game. We are Conservation Officers–Nova Scotia’s game wardens. Here to protect you, and your natural resources. Call 1-800-565-2224 to report illegal activity novascotia.ca/nse/conservation-enforcement Table of Contents Minister’s Message 2 New for 2018 3 Catch and Release 4 Special Management Areas 5 Proposed Changes for 2019 6 Seasons, Bag Limits, and Size Limits 7 General Regulations 9 Licences 11 Nova Scotia Recreational Fishing Areas Map 12-13 Recreational Fishing Area 1 18 Recreational Fishing Area 2 24 Recreational Fishing Area 3 28 Recreational Fishing Area 4 32 Recreational Fishing Area 5 40 Recreational Fishing Area 6 44 Winter Fishing Opportunities in Nova Scotia 48 The Freshwater Fisheries Research Cooperative 51 Inland Fisheries Division Activities 53 Tagged Fish 58 Definitions 59 Please Take Note ANGLERS’ HANDBOOK This is a summary prepared for the and 2018 Summary of Regulations information and convenience of the anglers of Nova Scotia. Consult the Wildlife Act, the Fisheries and Coastal Resources Act, and the Federal Fisheries Act and regulations New Licence Structure Free Sportfi shing for Residents and Weekends Non-Residents June 2–3, 2018 when interpreting and applying the law. These See page 11 for details February 16–18, 2019 regulations can change at any time. -

ABSTRACTS the Ecology and Genetics of Salmon Recovery: What Is Success? Ian A
WHAT WORKS? A Workshop on Wild Atlantic Salmon Recovery Programs September 18-19, 2013 Chamcook, New Brunswick ABSTRACTS The ecology and genetics of salmon recovery: what is success? Ian A. Fleming Department of Ocean Sciences, Memorial University of Newfoundland, St. John’s;[email protected] Atlantic salmon populations are becoming increasingly threatened, particularly across the species’ southern range. Recovery programs to rebuild these populations have met with varying “success.” Success, itself, can come to mean different things in different contexts. Here, I explore recovery in the context of salmon ecology and genetics. Characteristics that make salmon populations resilient to environmental change, whether such change is natural or anthropogenic, can provide a fundamental understanding of what recovery might look like. I look closely at one of the most commonly applied salmon recovery approaches for rebuilding salmon populations that involves artificial culture, i.e. hatcheries and living gene banks. The relationship, both ecological and genetic, between hatchery and wild fish is largely dependent on what occurs during breeding and its subsequent effects on offspring performance. I examine the roles of phenotypic plasticity, non-genetic inheritance and domestication in shaping and dictating the “success” of released hatchery fish and their ecological relationship with wild fish. Insight from DNA-based parentage assignment analyses on some early indicators of the efficacy of an adult-release stocking program on the Tobique River,