Great Circle Distances and Bearings Between Two Locations If We're Given Two Points a and B on the Earth (Assumed Spherical Wi
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
And Are Lines on Sphere B That Contain Point Q
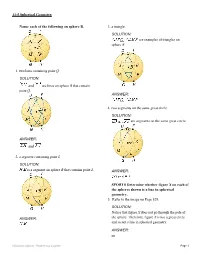
11-5 Spherical Geometry Name each of the following on sphere B. 3. a triangle SOLUTION: are examples of triangles on sphere B. 1. two lines containing point Q SOLUTION: and are lines on sphere B that contain point Q. ANSWER: 4. two segments on the same great circle SOLUTION: are segments on the same great circle. ANSWER: and 2. a segment containing point L SOLUTION: is a segment on sphere B that contains point L. ANSWER: SPORTS Determine whether figure X on each of the spheres shown is a line in spherical geometry. 5. Refer to the image on Page 829. SOLUTION: Notice that figure X does not go through the pole of ANSWER: the sphere. Therefore, figure X is not a great circle and so not a line in spherical geometry. ANSWER: no eSolutions Manual - Powered by Cognero Page 1 11-5 Spherical Geometry 6. Refer to the image on Page 829. 8. Perpendicular lines intersect at one point. SOLUTION: SOLUTION: Notice that the figure X passes through the center of Perpendicular great circles intersect at two points. the ball and is a great circle, so it is a line in spherical geometry. ANSWER: yes ANSWER: PERSEVERANC Determine whether the Perpendicular great circles intersect at two points. following postulate or property of plane Euclidean geometry has a corresponding Name two lines containing point M, a segment statement in spherical geometry. If so, write the containing point S, and a triangle in each of the corresponding statement. If not, explain your following spheres. reasoning. 7. The points on any line or line segment can be put into one-to-one correspondence with real numbers. -

Positional Astronomy Coordinate Systems
Positional Astronomy Observational Astronomy 2019 Part 2 Prof. S.C. Trager Coordinate systems We need to know where the astronomical objects we want to study are located in order to study them! We need a system (well, many systems!) to describe the positions of astronomical objects. The Celestial Sphere First we need the concept of the celestial sphere. It would be nice if we knew the distance to every object we’re interested in — but we don’t. And it’s actually unnecessary in order to observe them! The Celestial Sphere Instead, we assume that all astronomical sources are infinitely far away and live on the surface of a sphere at infinite distance. This is the celestial sphere. If we define a coordinate system on this sphere, we know where to point! Furthermore, stars (and galaxies) move with respect to each other. The motion normal to the line of sight — i.e., on the celestial sphere — is called proper motion (which we’ll return to shortly) Astronomical coordinate systems A bit of terminology: great circle: a circle on the surface of a sphere intercepting a plane that intersects the origin of the sphere i.e., any circle on the surface of a sphere that divides that sphere into two equal hemispheres Horizon coordinates A natural coordinate system for an Earth- bound observer is the “horizon” or “Alt-Az” coordinate system The great circle of the horizon projected on the celestial sphere is the equator of this system. Horizon coordinates Altitude (or elevation) is the angle from the horizon up to our object — the zenith, the point directly above the observer, is at +90º Horizon coordinates We need another coordinate: define a great circle perpendicular to the equator (horizon) passing through the zenith and, for convenience, due north This line of constant longitude is called a meridian Horizon coordinates The azimuth is the angle measured along the horizon from north towards east to the great circle that intercepts our object (star) and the zenith. -

Spherical Geometry
987023 2473 < % 52873 52 59 3 1273 ¼4 14 578 2 49873 3 4 7∆��≌ ≠ 3 δ � 2 1 2 7 5 8 4 3 23 5 1 ⅓β ⅝Υ � VCAA-AMSI maths modules 5 1 85 34 5 45 83 8 8 3 12 5 = 2 38 95 123 7 3 7 8 x 3 309 �Υβ⅓⅝ 2 8 13 2 3 3 4 1 8 2 0 9 756 73 < 1 348 2 5 1 0 7 4 9 9 38 5 8 7 1 5 812 2 8 8 ХФУШ 7 δ 4 x ≠ 9 3 ЩЫ � Ѕ � Ђ 4 � ≌ = ⅙ Ё ∆ ⊚ ϟϝ 7 0 Ϛ ό ¼ 2 ύҖ 3 3 Ҧδ 2 4 Ѽ 3 5 ᴂԅ 3 3 Ӡ ⍰1 ⋓ ӓ 2 7 ӕ 7 ⟼ ⍬ 9 3 8 Ӂ 0 ⤍ 8 9 Ҷ 5 2 ⋟ ҵ 4 8 ⤮ 9 ӛ 5 ₴ 9 4 5 € 4 ₦ € 9 7 3 ⅘ 3 ⅔ 8 2 2 0 3 1 ℨ 3 ℶ 3 0 ℜ 9 2 ⅈ 9 ↄ 7 ⅞ 7 8 5 2 ∭ 8 1 8 2 4 5 6 3 3 9 8 3 8 1 3 2 4 1 85 5 4 3 Ӡ 7 5 ԅ 5 1 ᴂ - 4 �Υβ⅓⅝ 0 Ѽ 8 3 7 Ҧ 6 2 3 Җ 3 ύ 4 4 0 Ω 2 = - Å 8 € ℭ 6 9 x ℗ 0 2 1 7 ℋ 8 ℤ 0 ∬ - √ 1 ∜ ∱ 5 ≄ 7 A guide for teachers – Years 11 and 12 ∾ 3 ⋞ 4 ⋃ 8 6 ⑦ 9 ∭ ⋟ 5 ⤍ ⅞ Geometry ↄ ⟼ ⅈ ⤮ ℜ ℶ ⍬ ₦ ⍰ ℨ Spherical Geometry ₴ € ⋓ ⊚ ⅙ ӛ ⋟ ⑦ ⋃ Ϛ ό ⋞ 5 ∾ 8 ≄ ∱ 3 ∜ 8 7 √ 3 6 ∬ ℤ ҵ 4 Ҷ Ӂ ύ ӕ Җ ӓ Ӡ Ҧ ԅ Ѽ ᴂ 8 7 5 6 Years DRAFT 11&12 DRAFT Spherical Geometry – A guide for teachers (Years 11–12) Andrew Stewart, Presbyterian Ladies’ College, Melbourne Illustrations and web design: Catherine Tan © VCAA and The University of Melbourne on behalf of AMSI 2015. -

08. Non-Euclidean Geometry 1
Topics: 08. Non-Euclidean Geometry 1. Euclidean Geometry 2. Non-Euclidean Geometry 1. Euclidean Geometry • The Elements. ~300 B.C. ~100 A.D. Earliest existing copy 1570 A.D. 1956 First English translation Dover Edition • 13 books of propositions, based on 5 postulates. 1 Euclid's 5 Postulates 1. A straight line can be drawn from any point to any point. • • A B 2. A finite straight line can be produced continuously in a straight line. • • A B 3. A circle may be described with any center and distance. • 4. All right angles are equal to one another. 2 5. If a straight line falling on two straight lines makes the interior angles on the same side together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the angles are together less than two right angles. � � • � + � < 180∘ • Euclid's Accomplishment: showed that all geometric claims then known follow from these 5 postulates. • Is 5th Postulate necessary? (1st cent.-19th cent.) • Basic strategy: Attempt to show that replacing 5th Postulate with alternative leads to contradiction. 3 • Equivalent to 5th Postulate (Playfair 1795): 5'. Through a given point, exactly one line can be drawn parallel to a given John Playfair (1748-1819) line (that does not contain the point). • Parallel straight lines are straight lines which, being in the same plane and being • Only two logically possible alternatives: produced indefinitely in either direction, do not meet one 5none. Through a given point, no lines can another in either direction. (The Elements: Book I, Def. -

The Celestial Sphere
The Celestial Sphere Useful References: • Smart, “Text-Book on Spherical Astronomy” (or similar) • “Astronomical Almanac” and “Astronomical Almanac’s Explanatory Supplement” (always definitive) • Lang, “Astrophysical Formulae” (for quick reference) • Allen “Astrophysical Quantities” (for quick reference) • Karttunen, “Fundamental Astronomy” (e-book version accessible from Penn State at http://www.springerlink.com/content/j5658r/ Numbers to Keep in Mind • 4 π (180 / π)2 = 41,253 deg2 on the sky • ~ 23.5° = obliquity of the ecliptic • 17h 45m, -29° = coordinates of Galactic Center • 12h 51m, +27° = coordinates of North Galactic Pole • 18h, +66°33’ = coordinates of North Ecliptic Pole Spherical Astronomy Geocentrically speaking, the Earth sits inside a celestial sphere containing fixed stars. We are therefore driven towards equations based on spherical coordinates. Rules for Spherical Astronomy • The shortest distance between two points on a sphere is a great circle. • The length of a (great circle) arc is proportional to the angle created by the two radial vectors defining the points. • The great-circle arc length between two points on a sphere is given by cos a = (cos b cos c) + (sin b sin c cos A) where the small letters are angles, and the capital letters are the arcs. (This is the fundamental equation of spherical trigonometry.) • Two other spherical triangle relations which can be derived from the fundamental equation are sin A sinB = and sin a cos B = cos b sin c – sin b cos c cos A sina sinb € Proof of Fundamental Equation • O is -

Appendix a Glossary
BASICS OF RADIO ASTRONOMY Appendix A Glossary Absolute magnitude Apparent magnitude a star would have at a distance of 10 parsecs (32.6 LY). Absorption lines Dark lines superimposed on a continuous electromagnetic spectrum due to absorption of certain frequencies by the medium through which the radiation has passed. AM Amplitude modulation. Imposing a signal on transmitted energy by varying the intensity of the wave. Amplitude The maximum variation in strength of an electromagnetic wave in one wavelength. Ångstrom Unit of length equal to 10-10 m. Sometimes used to measure wavelengths of visible light. Now largely superseded by the nanometer (10-9 m). Aphelion The point in a body’s orbit (Earth’s, for example) around the sun where the orbiting body is farthest from the sun. Apogee The point in a body’s orbit (the moon’s, for example) around Earth where the orbiting body is farthest from Earth. Apparent magnitude Measure of the observed brightness received from a source. Astrometry Technique of precisely measuring any wobble in a star’s position that might be caused by planets orbiting the star and thus exerting a slight gravitational tug on it. Astronomical horizon The hypothetical interface between Earth and sky, as would be seen by the observer if the surrounding terrain were perfectly flat. Astronomical unit Mean Earth-to-sun distance, approximately 150,000,000 km. Atmospheric window Property of Earth’s atmosphere that allows only certain wave- lengths of electromagnetic energy to pass through, absorbing all other wavelengths. AU Abbreviation for astronomical unit. Azimuth In the horizon coordinate system, the horizontal angle from some arbitrary reference direction (north, usually) clockwise to the object circle. -

Paths Between Points on Earth: Great Circles, Geodesics, and Useful Projections
Paths Between Points on Earth: Great Circles, Geodesics, and Useful Projections I. Historical and Common Navigation Methods There are an infinite number of paths between two points on the earth. For navigation purposes there are only a few historically common choices. 1. Sailing a latitude. Prior to a good method of finding longitude at sea, you sailed north or south until you cane to the latitude of your destination then you sailed due east or west until you reached your goal. Of course if you choose the wrong direction, you can get in big trouble. (This happened in 1707 to a British fleet that sunk when it hit rocks. This started the major British program for a longitude method useful at sea.) In this method the route follows the legs of a right triangle on the sphere. Just as in right triangles on the plane, the hypotenuse is always shorter than the sum of the other two sides. This method is very inefficient, but it was all that worked for open ocean sailing before 1770. 2. Rhumb Line A rhumb line is a line of constant bearing or azimuth. This is not the shortest distance on a long trip, but it is very easy to follow. You just have to know the correct azimuth to use to get between two sites, such as New York and London. You can get this from a straight line on a Mercator projection. This is the reason the Mercator projection was invented. On other projections straight lines are not rhumb lines. 3. Great Circle On a spherical earth, a great circle is the shortest distance between two locations. -

Great Circle
R E S O U R C E L I B R A R Y E N C Y C L O P E D I C E N T RY Great circle Encyclopedic entry. A great circle is the largest possible circle that can be drawn around a sphere. All spheres have great circles. G R A D E S 3 - 12+ S U B J E C T S Geography, Mathematics C O N T E N T S 3 Images For the complete encyclopedic entry with media resources, visit: http://www.nationalgeographic.org/encyclopedia/great-circle/ A great circle is the largest possible circle that can be drawn around a sphere. All spheres have great circles. If you cut a sphere at one of its great circles, you'd cut it exactly in half. A great circle has the same circumference, or outer boundary, and the same center point as its sphere. The geometry of spheres is useful for mapping the Earth and other planets. The Earth is not a perfect sphere, but it maintains the general shape. All the meridians on Earth are great circles. Meridians, including the prime meridian, are the north-south lines we use to help describe exactly where we are on the Earth. All these lines of longitude meet at the poles, cutting the Earth neatly in half. The Equator is another of the Earth's great circles. If you were to cut into the Earth right on its Equator, you'd have two equal halves: the Northern and Southern Hemispheres. The Equator is the only east-west line that is a great circle. -

A Comparison of Great Circle, Great Ellipse, and Geodesic Sailing
Journal of Marine Science and Technology, Vol. 21, No. 3, pp. 287-299 (2013) 287 DOI: 10.6119/JMST-012-0430-5 A COMPARISON OF GREAT CIRCLE, GREAT ELLIPSE, AND GEODESIC SAILING Wei-Kuo Tseng, Jiunn-Liang Guo, and Chung-Ping Liu Key words: great circle, great ellipse, geodesic, sailing. and course. Vincenty’s formulae [14] are two related iterative methods of nested equations used in geodesy to calculate the distance between two points on the surface of a spheroid, ABSTRACT developed by Thaddeus Vincenty in 1975. They are based on An analytical and numerical comparison of great circle the assumption that the figure of the Earth is an oblate (GC) sailing, great elliptic (GE) sailing, and geodesic (Geod) spheroid, and hence are more accurate than methods such as sailing is presented. The comparison between GC and GE great circle. The direct method computes the location of a sailing addresses some problems whether the navigator and point which is a given distance and course from another point. navigational software developers promptly have to use GE The inverse method computes the distance and course between sailing or use hybrid sailing mixed with features of the GC two given points. They have been widely used in geodesy sailing and GE sailing. This fact found here presents that because they are very accurate to within 0.5 mm on the the formulae tackling relationship of latitude and longitude of spheroidal Earth. GC sailing also can be suited to the GE sailing except some The discrepancies between the results on the GC sailing calculation of GE sailing involving distance and course. -

DIFFERENTIAL GEOMETRY of CURVES and SURFACES 7. Geodesics and the Theorem of Gauss-Bonnet 7.1
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 7. Geodesics and the Theorem of Gauss-Bonnet 7.1. Geodesics on a Surface. The goal of this section is to give an answer to the following question. Question. What kind of curves on a given surface should be the analogues of straight lines in the plane? Let’s understand first what means “straight” line in the plane. If you want to go from a point in a plane “straight” to another one, your trajectory will be such a line. In other words, a straight line has the property that if we fix two points P and Q on it, then the piece of between P Land Q is the shortest curve in the plane which joins the two points. Now, if insteadL of a plane (“flat” surface) you need to go from P to Q in a land with hills and valleys (arbitrary surface), which path will you take? This is how the notion of geodesic line arises: “Definition” 7.1.1. Let S be a surface. A curve α : I S parametrized by arc length → is called a geodesic if for any two points P = α(s1), Q = α(s2) on the curve which are sufficiently close to each other, the piece of the trace of α between P and Q is the shortest of all curves in S which join P and Q. There are at least two inconvenients concerning this definition: first, why did we say that P and Q are “sufficiently close to each other”?; second, this definition will certainly not allow us to do any explicit examples (for instance, find the geodesics on a hyperbolic paraboloid). -

Astronomy 518 Astrometry Lecture
Astronomy 518 Astrometry Lecture Astrometry: the branch of astronomy concerned with the measurement of the positions of celestial bodies on the celestial sphere, conditions such as precession, nutation, and proper motion that cause the positions to change with time, and corrections to the positions due to distortions in the optics, atmosphere refraction, and aberration caused by the Earth’s motion. Coordinate Systems • There are different kinds of coordinate systems used in astronomy. The common ones use a coordinate grid projected onto the celestial sphere. These coordinate systems are characterized by a fundamental circle, a secondary great circle, a zero point on the secondary circle, and one of the poles of this circle. • Common Coordinate Systems Used in Astronomy – Horizon – Equatorial – Ecliptic – Galactic The Celestial Sphere The celestial sphere contains any number of large circles called great circles. A great circle is the intersection on the surface of a sphere of any plane passing through the center of the sphere. Any great circle intersecting the celestial poles is called an hour circle. Latitude and Longitude • The fundamental plane is the Earth’s equator • Meridians (longitude lines) are great circles which connect the north pole to the south pole. • The zero point for these lines is the prime meridian which runs through Greenwich, England. PrimePrime meridianmeridian Latitude: is a point’s angular distance above or below the equator. It ranges from 90° north (positive) to 90 ° south (negative). • Longitude is a point’s angular position east or west of the prime meridian in units ranging from 0 at the prime meridian to 0° to 180° east (+) or west (-). -

Great Circle Distance Calculator
NAACCR 2006 Conference NAACCR SHOWCASE Great Circle Distance Calculator ChrisChris JohnsonJohnson NAACCRNAACCR GISGIS CommitteeCommittee CancerCancer DataData RegistryRegistry ofof IdahoIdaho Great Circle Distance Calculator WhatWhat isis it?it? HowHow dodo II useuse it?it? WhatWhat cancan II dodo withwith it?it? (in(in 1010 minutesminutes oror less)less) Great Circle Distance What is it? “The great circle distance is the shortest distance between any two points on the surface of the Earth measured along a path on the surface of the Earth.” “The distances are ‘as the crow flies’ if a crow could fly at sea level.” “The shape of the Earth closely resembles a flattened spheroid with extreme values for the radius of curvature of 6,336 km at the equator and 6,399 km at the poles.” “Using a sphere wwithith a radius of 6,367 km results in an error ooff up to about 00.5%..5%.” Huh?Huh? Great Circle Distance What is it? Better √ Good Best Great Circle Distance Calculator What is it? A SAS program that calculates the great circle distance between the locations of cases at the time of diagnosis and the locations of treatment facilities. Case locations are taken from NAACCR items 2352 (latitude) and 2354 (longitude) in a NAACCR v10 or v11 record layout file. The program can use either source (unconsolidated) or consolidated case records as input. A second input file (that you provide) contains facility IDs, latitude, and longitude. Great Circle Distance Calculator How do I use it? Great Circle Distance Calculator How do I use it? 1. AssumesAssumes youyou havehave geocodedgeocoded youryour cancercancer casescases -- ResidentialResidential addressaddress atat diagnosisdiagnosis 2.