Musical Scales: Thāṭ and Rāga
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Syllabus for MA (Previous) Hindustani Music Vocal/Instrumental
Syllabus for M.A. (Previous) Hindustani Music Vocal/Instrumental (Sitar, Sarod, Guitar, Violin, Santoor) SEMESTER-I Core Course – 1 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Historical and Theoretical Study of Ragas 70 Marks A. Historical Study of the following Ragas from the period of Sangeet Ratnakar onwards to modern times i) Gaul/Gaud iv) Kanhada ii) Bhairav v) Malhar iii) Bilawal vi) Todi B. Development of Raga Classification system in Ancient, Medieval and Modern times. C. Study of the following Ragangas in the modern context:- Sarang, Malhar, Kanhada, Bhairav, Bilawal, Kalyan, Todi. D. Detailed and comparative study of the Ragas prescribed in Appendix – I Internal Assessment 30 marks Core Course – 2 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Music of the Asian Continent 70 Marks A. Study of the Music of the following - China, Arabia, Persia, South East Asia, with special reference to: i) Origin, development and historical background of Music ii) Musical scales iii) Important Musical Instruments B. A comparative study of the music systems mentioned above with Indian Music. Internal Assessment 30 marks Core Course – 3 Practical Credit - 8 Practical : 70 Internal Assessment : 30 Maximum Marks : 100 Stage Performance 70 marks Performance of half an hour’s duration before an audience in Ragas selected from the list of Ragas prescribed in Appendix – I Candidate may plan his/her performance in the following manner:- Classical Vocal Music i) Khyal - Bada & chota Khyal with elaborations for Vocal Music. Tarana is optional. Classical Instrumental Music ii) Alap, Jor, Jhala, Masitkhani and Razakhani Gat with eleaborations Semi Classical Music iii) A short piece of classical music /Thumri / Bhajan/ Dhun /a gat in a tala other than teentaal may also be presented. -
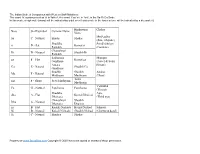
Note Staff Symbol Carnatic Name Hindustani Name Chakra Sa C
The Indian Scale & Comparison with Western Staff Notations: The vowel 'a' is pronounced as 'a' in 'father', the vowel 'i' as 'ee' in 'feet', in the Sa-Ri-Ga Scale In this scale, a high note (swara) will be indicated by a dot over it and a note in the lower octave will be indicated by a dot under it. Hindustani Chakra Note Staff Symbol Carnatic Name Name MulAadhar Sa C - Natural Shadaj Shadaj (Base of spine) Shuddha Swadhishthan ri D - flat Komal ri Rishabh (Genitals) Chatushruti Ri D - Natural Shudhh Ri Rishabh Sadharana Manipur ga E - Flat Komal ga Gandhara (Navel & Solar Antara Plexus) Ga E - Natural Shudhh Ga Gandhara Shudhh Shudhh Anahat Ma F - Natural Madhyam Madhyam (Heart) Tivra ma F - Sharp Prati Madhyam Madhyam Vishudhh Pa G - Natural Panchama Panchama (Throat) Shuddha Ajna dha A - Flat Komal Dhaivat Dhaivata (Third eye) Chatushruti Shudhh Dha A - Natural Dhaivata Dhaivat ni B - Flat Kaisiki Nishada Komal Nishad Sahsaar Ni B - Natural Kakali Nishada Shudhh Nishad (Crown of head) Så C - Natural Shadaja Shadaj Property of www.SarodSitar.com Copyright © 2010 Not to be copied or shared without permission. Short description of Few Popular Raags :: Sanskrut (Sanskrit) pronunciation is Raag and NOT Raga (Alphabetical) Aroha Timing Name of Raag (Karnataki Details Avroha Resemblance) Mood Vadi, Samvadi (Main Swaras) It is a old raag obtained by the combination of two raags, Ahiri Sa ri Ga Ma Pa Ga Ma Dha ni Så Ahir Bhairav Morning & Bhairav. It belongs to the Bhairav Thaat. Its first part (poorvang) has the Bhairav ang and the second part has kafi or Så ni Dha Pa Ma Ga ri Sa (Chakravaka) serious, devotional harpriya ang. -

ANSWERED ON:25.11.2014 TOURIST SITES Singh Shri Rama Kishore
GOVERNMENT OF INDIA TOURISM LOK SABHA UNSTARRED QUESTION NO:403 ANSWERED ON:25.11.2014 TOURIST SITES Singh Shri Rama Kishore Will the Minister of TOURISM be pleased to state: (a) whether tourist sites have been categorised grade-wise in the country and if so, the details thereof; (b) the details of tourist sites covered under Buddhist circuit and developed as world heritage tourist sites during the last three years and the current year; (c) whether the Government has any tourism related proposals for Vaishali in Bihar including financial assistance; and (d) if so, the details thereof? Answer MINISTER OF STATE FOR TOURISM (INDEPENDENT CHARGE) (DR. MAHESH SHARMA) (a): Madam. At present there is no grade wise categorization of tourist sites. (b): The Ministry of Tourism has identified following three circuits to be developed as Buddhist Circuits in the country with the help of Central Government/State Government/Private stake holders: Circuit 1: The Dharmayatra or the Sacred Circuit - This will be a 5 to 7 days circuit and will include visits to Gaya (Bodhgaya), Varanasi (Sarnath), Kushinagar, Piparva (Kapilvastu) with a day trip to Lumbini in Nepal. Circuit 2: Extended Dharmayatra or Extended Sacred Circuit or Retracing Buddha's Footsteps - This will be a 10 to 15 day circuit and will include visits to Bodhgaya (Nalanda, Rajgir, Barabar caves, Pragbodhi Hill, Gaya), Patna (Vaishali, Lauriya Nandangarh, Lauriya Areraj, Kesariya, Patna Museum), Varanasi (Sarnath), Kushinagar, Piparva (Kapilvastu, Shravasti, Sankisa) with a day trip to Lumbini in Nepal. Circuit 3: Buddhist Heritage Trails (State Circuits). i. Jammu and Kashmir - Ladakh, Srinagar (Harwan, Parihaspora) and Jammu (Ambaran). -

Ragang Based Raga Identification System
IOSR Journal Of Humanities And Social Science (IOSR-JHSS) Volume 16, Issue 3 (Sep. - Oct. 2013), PP 83-85 e-ISSN: 2279-0837, p-ISSN: 2279-0845. www.Iosrjournals.Org Ragang based Raga Identification system Awadhesh Pratap Singh Tomer Assistant Professor (Music-vocal), Department of Music Dr. H. S. G. Central University Sagar M.P. Gopal Sangeet Mahavidhyalaya Mahaveer Chowk Bina Distt. Sagar (M.P.) 470113 Abstract: The paper describes the importance of Ragang in the Raga classification system and its utility as being unique musical patterns; in raga identification. The idea behind the paper is to reinvestigate Ragang with a prospective to use it in digital classification and identification system. Previous works in this field are based on Swara sequence and patterns, Pakad and basic structure of Raga individually. To my best knowledge previous works doesn’t deal with the Ragang Patterns for identification and thus the paper approaches Raga identification with a Ragang (musical pattern group) base model. This work also reviews the Thaat-Raagang classification system. This describes scope in application for Automatic digital teaching of classical music by software program to analyze music (Classical vocal and instrumental). The Raag classification should be flawless and logically perfect for best ever results. Key words: Aadhar shadaj, Ati Komal Gandhar , Bahar, Bhairav, Dhanashri, Dhaivat, Gamak, Gandhar, Gitkarri, Graam, Jati Gayan, Kafi, Kanada, Kann, Komal Rishabh , Madhyam, Malhar, Meed, Nishad, Raga, Ragang, Ragini, Rishabh, Saarang, Saptak, Shruti, Shrutiantra, Swaras, Swar Prastar, Thaat, Tivra swar, UpRag, Vikrat Swar A Raga is a tonal frame work for composition and improvisation. It embodies a unique musical idea.(Balle and Joshi 2009, 1) Ragang is included in 10 point Raga classification of Saarang Dev, With Graam Raga, UpRaga and more. -

Stephen M. Slawek Curriculum Vitae
Stephen M. Slawek Curriculum Vitae 10008 Sausalito Drive Butler School of Music Austin, TX 78759-6106 The University of Texas at Austin (512) 794-2981 Austin, TX. 78712-0435 (512) 471-0671 Education 1986 Ph.D. (Ethnomusicology) University of Illinois at Urbana-Champaign 1978 M.A. (Ethnomusicology) University of Hawaii at Manoa 1976 M. Mus. (Sitar) Banaras Hindu University 1974 B. Mus. (Sitar) Banaras Hindu University 1973 Diploma (Tabla) Banaras Hindu University 1971 B.A. (Biology) University of Pennsylvania Employment 1999-present Professor of Ethnomusicology, The University of Texas at Austin 2000 Visiting Professor, Rice University, Hanzsen and Lovett College 1989-1999 Associate Professor of Ethnomusicology and Asian Studies, The University of Texas at Austin 1985-1989 Assistant Professor of Ethnomusicology and Asian Studies, The University of Texas at Austin 1983-1985 Instructor of Ethnomusicology and Asian Studies, The University of Texas at Austin 1983 Visiting Lecturer of Ethnomusicology, University of Illinois at Urbana- Champaign 1982 Graduate Assistant, School of Music, University of Illinois at Urbana- Champaign 1978-1980 Archivist, Archives of Ethnomusicology, School of Music, University of Illinois at Urbana-Champaign Scholarship and Creative Activities Books under contract The Classical Music of India: Going Global with Ravi Shankar. New York and London: Routledge Press. 1997 Musical Instruments of North India: Eighteenth Century Portraits by Baltazard Solvyns. Delhi: Manohar Publishers. Pp. i-vi and 1-153. (with Robert L. Hardgrave) SLAWEK- curriculum vitae 2 1987 Sitar Technique in Nibaddh Forms. New Delhi: Motilal Banarsidass, Indological Publishers and Booksellers. Pp. i-xix and 1-232. Articles in scholarly journals 1996 In Raga, in Tala, Out of Culture?: Problems and Prospects of a Hindustani Musical Transplant in Central Texas. -

New Trends in Hindustani Sitar Music in Malaysia
23 Towards Fusion: New Trends in Hindustani Sitar Music in Malaysia Pravina Manoharan Universiti Sains Malaysia Abstract While a classical Sitar recital in Malaysia still retains many of its original forms and practices, local sitarists are experimenting with new musical ideas to promote the Sitar and its music to a wider audience of mixed ethnicity. Musicians combine Hindustani musical elements such as Raag (melody) and Taal (rhythmic cycle) with different musical elements such as the Chinese pentatonic scale and Arabian Maqam as well as new genres to produce a musical blend broadly dubbed as ‘fusion music’. This article explores how the characteristics of the Hindustani elements of Raag and Taal are adopted to complement the structure and style of the new compositions. Different Sitar playing styles and techniques are employed in the performance of fusion compositions that use Blues or Bossa Nova genres. Keywords: Raag, Taal, fusion, Sitar music. 24 Wacana Seni Journal of Arts Discourse. Jil./Vol.7.2008 Introduction Malaysia is a multiracial and multicultural society that has a rich and diverse cultural and musical heritage. Indians represent the third largest population in the country. The classical music practiced by Malaysian Indians is based on the ancient traditional system that originated in India. Indian classical music refers to both the South Indian Carnatic and North Indian Hindustani systems. Hindustani and Carnatic music share a common ancient musical heritage, as both systems are built upon highly complex and elaborate melodic structures called Raag, and both employ a system of rhythm and meter that falls under the rubric of Taal (rhythmic cycle). -

National Sanskrit University, Tirupati
National Sanskrit University, Tirupati, (Central University) Department of performing arts Indian Classical Instrumental Music On-line Certificate Programme for Six month Subject- Sitar Programme Details: Name of the Programme : On-line Certificate Programme in Sitar Duration of the Programme : 6 Months (July to December) 2020 Level 1:- July - August. Level 2:- September - October. Level 3:- November - December. Time allocation : Indian Students: - 1 hour class for a day (3 days in a week.) Abroad students: - 1 hour class for a day (3 days in a week.) Mode of Examination : On-line No. of Papers : Two types of papers each Level . 1st Paper: Practical . 2nd Paper: Applied Viva *Including One Theory paper in 3rd level Total Marks : 300 marks For 3 Level. Each Level Carry 75 Marks. 1st Paper: Practical: 50 Marks . 2nd Paper: Applied Viva: 25 Marks *Applied Theory paper in 3rd level 75 Marks Programme Fee : Onetime payment for 1, 2, 3 Level For Indian Student: - INR – 3000/- For Abroad Student: - INR - 5000/- Eligibility : Age 12 to 50 Years Medium of Instruction : Hindi, English Number of Seats : 20 (Based on merit in audition test) Presets for Learning : Students are required to have sitar essentials. (Students can keep any mobile app for shruti, Rhythm metronome, Guitar tuners) Programme Coordinator : Dr. Hans Prabhakar Ravidas Assistant Professor Department of Performing Arts Instrumental Music (Sitar) National Sanskrit University, Tirupat, Andhra Pradesh, India Mobile- 8127759391, Mail- [email protected] More information can be found on the website of the university: www.nsktu.ac.in Registration: https://forms.gle/3cwDY1JCdC9UzfYr7 Level 1 Prescribed Syllabus 1. Introduction of sitar with structure. -

Zakir Hussain & Masters of Percussion
CAL PERFORMANCES PRESENTS Sunday, March 23, 2014, 7pm Zellerbach Hall Zakir Hussain & Masters of Percussion with Zakir Hussain tabla Selvaganesh Vinayakram kanjira & ghatam Steve Smith Western drums Niladri Kumar sitar Dilshad Khan sarangi Deepak Bhatt dhol Vijay Chavan dholki and special guest Antonia Minnecola Kathak dancer PROGRAM Tonight’s program will be announced from the stage. There will be one intermission. Cal Performances’ – season is sponsored by Wells Fargo. PLAYBILL ABOUT THE ARTISTS The foremost disciple of his father, the leg- endary Ustad Allarakha, Mr. Hussain was a child prodigy who began his professional career at the age of twelve and had toured internation- ally with great success by the age of 18. He has been the recipient of many awards, grants and honors, including Padma Bhushan (2002), Padma Shri (1988), the Sangeet Natak Akademi Award (1991), Kalidas Samman (2006), the 1999 National Heritage Fellowship Award, the Bay Area Isadora Duncan Award (1998–1999), and Grammy Awards in 1991 and 2009 for Best World Music Album for Planet Drum and Global Drum Project, both collaborations with Mickey Hart. His music and extraordinary con- tribution to the music world were honored in April 2009, with four widely heralded and sold- out concerts in Carnegie Hall’s “Perspectives” series. Also in 2009, Mr. Hussain was named a Susana Millman Susana Member in the Order of Arts and Letters by AKIR HUSSAIN (tabla) is today appreciated France’s Ministry of Culture and Commun - Zboth in the field of percussion and in the ication. Most recently, the National Symphony music world at large as an international phe- Orchestra with Christoph Eschenbach com- nomenon. -

7376 Sitar and Surbahar
(LYRCD 7376) SITAR AND SURBARHAR Indian Music for Meditation and Love Ustad Imrat Khan, Sitar and Surbahar Shafaat Miadaad Khan, Tabla In this, his first recording made in the United State, Imrat Khan demonstrates his consummate mastery of two instruments, the sitar and the surbahar, the bass sitar, which he introduced to the American concert stage in 1975. Both the sitar and surbahar have developed from the oldest stringed instrument of India, the bin or rudra vina, which consists of two large gourds of equal size joined symmetrically by a round wooden neck. The bin is characterized by its deep, rich voice. The sitar hardly needs introduction to western audiences, but it is worth noting in connection with this recording that there are two basic styles of stringing the instrument to approximate the sound of the bin. In the second style, popularized by Imrat Khan’s family, there are only six main strings with a range of three octaves, on the grounds that the deep tones of the surbahar recreate more effectively the bin’s lower register. The Surbahar was invented by Imrat Khan’s great-grandfather, Ustad Sahebdad Khan. The instrument was in danger of disappearing after the death of Enayet Khan, Imrat’s father; but thanks to the efforts of Imrat himself, the instrument has regained its place as one of the most important instruments of North Indian art music. The surbahar is, in effect, a bass sitar, with a practical range of over four octaves. It has a wider neck, thicker strings, and a gourd larger and flatter than that of the sitar. -

Buddhism in the Northern Deccan Under The
BUDDHISM IN THE NORTHERN DECCAN UNDER THE SATAVAHANA RULERS C a ' & C > - Z Z f /9> & by Jayadevanandasara Hettiarachchy Thesis submitted for the Degree of Doctor of Philosophy to the University of London 1973* ProQuest Number: 10731427 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 10731427 Published by ProQuest LLC(2017). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 ABSTRACT This study deals with the history of Buddhism in the northern Deccan during the Satavahana period. The first chapter examines the evidence relating to the first appearance of Buddhism in this area, its timing and the support by the state and different sections of the population. This is followed by a discussion of the problems surrounding the chronology of the Satavahana dynasty and evidence is advanced to support the ’shorter chronology*. In the third chapter the Buddhist monuments attributable to the Satavahana period are dated utilising the chronology of the Satavahanas provided in the second chapter. The inscriptional evidence provided by these monuments is described in detail. The fourth chapter contains an analysis and description of the sects and sub-sects which constituted the Buddhist Order. -

Transcription and Analysis of Ravi Shankar's Morning Love For
Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 2013 Transcription and analysis of Ravi Shankar's Morning Love for Western flute, sitar, tabla and tanpura Bethany Padgett Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_dissertations Part of the Music Commons Recommended Citation Padgett, Bethany, "Transcription and analysis of Ravi Shankar's Morning Love for Western flute, sitar, tabla and tanpura" (2013). LSU Doctoral Dissertations. 511. https://digitalcommons.lsu.edu/gradschool_dissertations/511 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Doctoral Dissertations by an authorized graduate school editor of LSU Digital Commons. For more information, please [email protected]. TRANSCRIPTION AND ANALYSIS OF RAVI SHANKAR’S MORNING LOVE FOR WESTERN FLUTE, SITAR, TABLA AND TANPURA A Written Document Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Musical Arts in The School of Music by Bethany Padgett B.M., Western Michigan University, 2007 M.M., Illinois State University, 2010 August 2013 ACKNOWLEDGEMENTS I am entirely indebted to many individuals who have encouraged my musical endeavors and research and made this project and my degree possible. I would first and foremost like to thank Dr. Katherine Kemler, professor of flute at Louisiana State University. She has been more than I could have ever hoped for in an advisor and mentor for the past three years. -

Updated in June, 2016 SALE COUNTERS OF
Updated in June, 2016 SALE COUNTERS OF ARCHAEOLOGICAL SURVEY OF INDIA IN INDIA Total Sale Counters : 107 Sl. Circle/Branch/Office Place of Sale Counter Address of Sale Counter No. 1. ASI, Hqrs, Office, New Directorate Office Janpath, New Delhi - 110 011 Delhi (1) 2. Agra Circle (5) Shilpgram Eastern Gate, O/o Conservation Asstt. ASI, Sub- Taj Mahal Circle, Taj Mahal, Agra Agra Fort O/o Conservation Asstt. ASI, Sub- Circle, Agra Fort, Agra Fatehpur Sikri O/o Conservation Asstt. ASI, Sub- Circle, Fatehpur Sikri, Agra Sikandra, Agra O/o Conservation Asstt. ASI, Sub- Circle, Sikandra, Agra Itimadaulla O/o Conservation Asstt. ASI, Sub- Circle, Itimadaulla, Agra 3. Aurangabad Circle (6) Along with Booking O/o The Sr. Conservation Assistant Counter Archaeological Survey of India, Ajanta Caves, Ajanta Ajanta Sub-Circle, Ajanta, Post : Faradapur - 431 118 District : Aurangabad - 431004 Along with Booking O/o The Sr. Conservation Assistant Counter Archaeological Survey of India, Ellora Caves, Ellora Ellora Sub-Circle, Ellora, Taluka : Khultabad District : Aurangabad - 431 004 Along with Booking O/o The Jr. Conservation Assistant Counter Archaeological Survey of India, Bibi-ka-Maqbara, Bibi-ka-Maqbara Sub-Circle, Aurangabad Begampura, District : Aurangabad - 431 004 Along with Booking O/o The Jr. Conservation Assistant Counter Archaeological Survey of India, Daulatabad Fort, Daultabad Fort Ta Aurangabad Daulatabad Dist. Aurangabad - 431 002 Along with Booking O/o The Sr. Conservation Assistant Counter Archaeological Survey of India, Pnadavlena Caves, Nasik Sub-Circle, Ambed, District : Nasik Nasik - 422 010 Along with Booking Archaeological Survey of India, Counter Aurangabad Caves, Aurangabad, Aurangabad Caves District : Aurangabad - 431 004 4.