Combining Mean Reversion and Momentum Trading Strategies In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Future of Computer Trading in Financial Markets an International Perspective
The Future of Computer Trading in Financial Markets An International Perspective FINAL PROJECT REPORT This Report should be cited as: Foresight: The Future of Computer Trading in Financial Markets (2012) Final Project Report The Government Office for Science, London The Future of Computer Trading in Financial Markets An International Perspective This Report is intended for: Policy makers, legislators, regulators and a wide range of professionals and researchers whose interest relate to computer trading within financial markets. This Report focuses on computer trading from an international perspective, and is not limited to one particular market. Foreword Well functioning financial markets are vital for everyone. They support businesses and growth across the world. They provide important services for investors, from large pension funds to the smallest investors. And they can even affect the long-term security of entire countries. Financial markets are evolving ever faster through interacting forces such as globalisation, changes in geopolitics, competition, evolving regulation and demographic shifts. However, the development of new technology is arguably driving the fastest changes. Technological developments are undoubtedly fuelling many new products and services, and are contributing to the dynamism of financial markets. In particular, high frequency computer-based trading (HFT) has grown in recent years to represent about 30% of equity trading in the UK and possible over 60% in the USA. HFT has many proponents. Its roll-out is contributing to fundamental shifts in market structures being seen across the world and, in turn, these are significantly affecting the fortunes of many market participants. But the relentless rise of HFT and algorithmic trading (AT) has also attracted considerable controversy and opposition. -

Keep up the Momentum∗
Keep Up The Momentum∗ Thierry Roncalli Quantitative Research Amundi Asset Management, Paris [email protected] December 2017 Abstract The momentum risk premium is one of the most important alternative risk premia alongside the carry risk premium. However, it appears that it is not always well under- stood. For example, is it an alpha or a beta exposure? Is it a skewness risk premium or a market anomaly? Does it pursue a performance objective or a hedging objective? What are the differences between time-series and cross-section momentum? What are the main drivers of momentum returns? What does it mean when we say that it is a convex and not a concave strategy? Why is the momentum risk premium a diversifying engine, and not an absolute return strategy? The goal of this paper is to provide specific and relevant answers to all these ques- tions. The answers can already be found in the technical paper \Understanding the Momentum Risk Premium" published recently by Jusselin et al. (2017). However, the underlying mathematics can be daunting to readers. Therefore, this discussion paper presents the key messages and the associated financial insights behind these results. Among the main findings, one result is of the most importance. To trend is to diversify in bad times. In good times, trend-following strategies offer no significant diversification power. Indeed, they are beta strategies. This is not a problem, since investors do not need to be diversified at all times. In particular, they do not need diversification in good times, because they do not want that the positive returns gen- erated by some assets to be cancelled out by negative returns on other assets. -

Explanations for the Momentum Premium
CAPITAL MANAGEMENT Tobias Moskowitz, Ph.D. Summer 2010 Fama Family Professor of Finance University of Chicago Booth School of Business EXPLANATIONS FOR THE MOMENTUM PREMIUM Momentum is a well established empirical fact whose premium is evident in over 83 years of U.S. data, in 20 years of out of sample evidence from its original discovery, in 40 other countries, and in more than a dozen other asset classes. Its presence and robustness are remarkably stable and, along with the size and value premia, these investment styles have become the preeminent empirical regularities studied by academics and practitioners. And, like size and value, there is much debate and little consensus regarding the explanation driving this premium, though there are some compelling theories. In this short note, we summarize briefly the risk-based and non-risk based explanations for momentum. While the jury is still out on which of these explanations better fit the data, we emphasize that similar uncertainty regarding the explanation behind the size and value premium also exists. Much like momentum, stories for the size and value premium range from risk-based to behavioral and there is a healthy debate over which of these theories is most consistent with the facts. These debates are likely to continue for the foreseeable future, but as we discuss below there are many viable candidate theories for their existence—and the truth behind the source of these premia probably contains elements from several explanations. Non Risk-Based Explanations Some argue that the momentum premium is driven by non-risk factors, many of which have a behavioral flavor. -

Absolute Momentum: a Simple Rule-Based Strategy and Universal Trend-Following Overlay
Absolute Momentum: a Simple Rule-Based Strategy and Universal Trend-Following Overlay Gary Antonacci Portfolio Management Associates, LLC1 February 28, 2013 Abstract There is a considerable body of research on relative strength price momentum but relatively little on absolute, time series momentum. In this paper, we explore the practical side of absolute momentum. We first explore its sole parameter - the formation, or look back, period. We then examine the reward, risk, and correlation characteristics of absolute momentum applied to stocks, bonds, and real assets. We finally apply absolute momentum to a 60-40 stock/bond portfolio and a simple risk parity portfolio. We show that absolute momentum can effectively identify regime change and add significant value as an easy to implement, rule-based approach with many potential uses as both a stand- alone program and trend following overlay. 1 http://optimalmomentum.com 1 1. Introduction The cross-sectional momentum effect is one of the strongest and most pervasive financial phenomena (Jegadeesh and Titman (1993), (2001)). Researchers have verified its value with many different asset classes, as well as across groups of assets (Blitz and Van Vliet (2008), Asness, Moskowitz and Pedersen (2012)). Since its publication, momentum has held up out-of-sample going forward in time (Grundy and Martin (2001), Asness, Moskowitz and Pedersen (2012)) and back to the Victorian Age (Chabot, Ghysels, and Jagannathan (2009)). In addition to cross-sectional momentum, in which an asset's performance relative to other assets predicts its future relative performance, momentum also works well on an absolute, or time series basis, in which an asset's own past return predicts its future performance. -

Perspectives on the Equity Risk Premium – Siegel
CFA Institute Perspectives on the Equity Risk Premium Author(s): Jeremy J. Siegel Source: Financial Analysts Journal, Vol. 61, No. 6 (Nov. - Dec., 2005), pp. 61-73 Published by: CFA Institute Stable URL: http://www.jstor.org/stable/4480715 Accessed: 04/03/2010 18:01 Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/page/info/about/policies/terms.jsp. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/action/showPublisher?publisherCode=cfa. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. CFA Institute is collaborating with JSTOR to digitize, preserve and extend access to Financial Analysts Journal. http://www.jstor.org FINANCIAL ANALYSTS JOURNAL v R ge Perspectives on the Equity Risk Premium JeremyJ. -
Commodities Favored with Mean Reversion
Market Commentary 1 Energy 3 Bloomberg Commodity Index (BCOM) Metals 6 Agriculture 11 Tables & Charts – January 2018 Edition DATA PERFORMANCE: 14 Overview, Commodity TR, Prices, Volatility Commodities Favored With CURVE ANALYSIS: 18 Contango/Backwardation, Roll Yields, Mean Reversion Forwards/Forecasts MARKET FLOWS: 21 Open Interest, Volume, - Commodities hitting stride with weak greenback, inflation & economic growth COT, ETFs - Energy is a bit too hot, agriculture too cold, metals the steady bull - Commodities set to shine when volatility returns to financial markets - Strong precious vs. industrial metals may be anticipating a bit of stock market normalization Gold Outlook 2018 Webinar, February 22, 11: 00 am EST https://platform.cinchcast.com/ses/s6SMtqZXpK0t3tNec9WLoA~~ Mike McGlone – BI Senior Commodity Strategist BI COMD (the commodity dashboard) Mean Reversion, a Potential Key 2018 Commodity Bull Gaining Stride Theme, Favors Commodities Crude to Copper: Commodity Relative-Value Performance: January +2.0%, Spot +1.9%. Foundation Is Firming. Agriculture is favored vs. energy, (Returns are total return (TR) unless noted) at least in the shorter term, with mean-reversion overdue in corn, the commodity with the most net-short positions, (Bloomberg Intelligence) -- The commodity bull market vs. crude oil (the longest). Energy should stabilize, metals should be just hitting its stride. Relative to its primary remain strong, and grains are ripe to advance about a drivers -- a declining dollar, rising inflation, demand third on some weather normalization. exceeding supply and expanding global economic growth -- the Bloomberg Commodity Spot Index's four-year high Commodities should have an advantage in 2018 vs. in January is on the right path. -

Do Momentum-Based Strategies Still Work in Foreign Currency Markets?
JOURNAL OF FINANCIAL AND QUANTTTATIVE ANALYSIS VOL 38, NO. 2. JUNE 2003 COPr-HIQHT 2003. SCHCXH. OF BUSINESS ADMINISTRATION. UNIVERSITY OF WASHINGTON. SEATTLE, WA 98195 Do Momentum-Based Strategies Still Work in Foreign Currency Markets? John Okunev and Derek White* Abstract This paper examines the peifonnance of momentum trading strategies in foreign enchange markets. We find the well-documented profitability of momentum strategies during the 1970s and the 1980s has continued throughout the 1990s. Our ap(soach and findings are insensitive to die specification of the trading nile and the hase currency for analysis. Finally, we show that the peifonnance is not due to a time-vaiying risk premium hut rather depends on the underlying autocorrelation structure of the currency returns. In sum, the results lend fimher supprat to prior momentum studies on equities. The profitability to momentum-based strategies holds for currencies as well. I. Introduction For over three decades, investors in foreign exchange maikets have disagreed with the academic helief that price hehavior is entirely detennined hy market fundamentals. While most would concur that over the long run exchange rates should reflect fundamental value, many hold tbe view that short-t«m profitable opportunities exist due to market inefficiencies. In this paper, we examine the profitability of momentum trading strategies in foreign exchange maikets. * We find the well-documented profitability of momentum strategies during tbe 1970s and the 1980s has continued throughout the 1990s. Furthermore, we find that this profitability is not due to compensation for bearing a dme-varying risk premium. A degree of maricet inefficiency must be present in foreign exchange mar- kets for technical trading strategies to generate positive risk-adjusted returns. -

There's More to Volatility Than Volume
There's more to volatility than volume L¶aszl¶o Gillemot,1, 2 J. Doyne Farmer,1 and Fabrizio Lillo1, 3 1Santa Fe Institute, 1399 Hyde Park Road, Santa Fe, NM 87501 2Budapest University of Technology and Economics, H-1111 Budapest, Budafoki ut¶ 8, Hungary 3INFM-CNR Unita di Palermo and Dipartimento di Fisica e Tecnologie Relative, Universita di Palermo, Viale delle Scienze, I-90128 Palermo, Italy. It is widely believed that uctuations in transaction volume, as reected in the number of transactions and to a lesser extent their size, are the main cause of clus- tered volatility. Under this view bursts of rapid or slow price di®usion reect bursts of frequent or less frequent trading, which cause both clustered volatility and heavy tails in price returns. We investigate this hypothesis using tick by tick data from the New York and London Stock Exchanges and show that only a small fraction of volatility uctuations are explained in this manner. Clustered volatility is still very strong even if price changes are recorded on intervals in which the total transaction volume or number of transactions is held constant. In addition the distribution of price returns conditioned on volume or transaction frequency being held constant is similar to that in real time, making it clear that neither of these are the principal cause of heavy tails in price returns. We analyze recent results of Ane and Geman (2000) and Gabaix et al. (2003), and discuss the reasons why their conclusions di®er from ours. Based on a cross-sectional analysis we show that the long-memory of volatility is dominated by factors other than transaction frequency or total trading volume. -

Are Momentum Profits Driven by Dividend Strategy?
2018-0859 IJOI http://www.ijoi-online.org/ ARE MOMENTUM PROFITS DRIVEN BY DIVIDEND STRATEGY? Huei-Hwa Lai Department of Finance National Yunlin University of Science and Technology, Taiwan R.O.C. Szu-Hsien Lin* Department of Finance TransWorld University, Taiwan R.O.C. *Corresponding Author: [email protected] Ai-Chi Hsu Department of Finance National Yunlin University of Science and Technology, Taiwan R.O.C. Abstract In this paper, we investigate the effects of dividend policy in determining price mo- mentum. Our evidence shows that trading strategies based on buying dividend-paying (dividend increasers, dividend cutters or dividend maintainers) stocks combined with the winner and loser momentum strategy generate positive and significant profits that are substantially higher than those from the traditional winner and loser momentum strategy. The buying-winner and selling-loser portfolios in Taiwan do not exhibit momentum profits, but exhibit contrarian profits for holding longer periods. In addi- tion, we show that dividend policy has trading effects in determining price momentum in mid-term holding period (more than 6 months). If combined with higher formation period returns (top 50 winners), the momentum profits of dividend increasers are higher than those of dividend maintainers. Finally, investors reward companies when they have a change in dividend policy rather than just maintain their dividend levels. Keywords: Finance, Dividend Policy, Price Momentum, Price Contrarian, Behavioral Finance 1 The International Journal of Organizational Innovation Vol 11 Num 1 July 2018 2018-0859 IJOI http://www.ijoi-online.org/ Introduction justed profits. They also show that the dividend-increasing announcements en- Our study focuses on the influence hance the winners’ momentum profits, of dividend policy on stock market mo- and dividend-decreasing announcements mentum. -

The Role of Investability Restrictions on Size, Value, and Momentum in International Stock Returns
The Role of Investability Restrictions on Size, Value, and Momentum in International Stock Returns by G. Andrew Karolyi and Ying Wu* Abstract Using monthly returns for over 37,000 stocks from 46 developed and emerging market countries over a two- decade period, we test whether empirical asset pricing models capture the size, value, and momentum patterns in international stock returns. We propose and test a multi-factor model that includes factor portfolios based on firm characteristics and that builds separate factors comprised of globally-accessible stocks, which we call “global factors,” and of locally-accessible stocks, which we call “local factors.” Our new “hybrid” multi-factor model with both global and local factors not only captures strong common variation in global stock returns, but also achieves low pricing errors and rejection rates using conventional testing procedures for a variety of regional and global test asset portfolios formed on size, value, and momentum. First Version: November 23, 2011. This Version: November 14, 2012. Key words: International asset pricing; investment restrictions; cross-listed stocks. JEL Classification Codes: F30, G11, G15. * Karolyi is Professor of Finance and Economics and Alumni Chair in Asset Management at the Johnson Graduate School of Management, Cornell University and Wu is a Ph.D. student, Department of Economics, Cornell University. We are grateful for detailed comments from Ken French, for useful conversations with Francesca Carrieri, Bernard Dumas,Vihang Errunza, Cheol Eun, Gene Fama, Kingsley Fong, Amit Goyal, John Griffin, Kewei Hou, Bong-Chan Kho, Robert Kieschnick, Pam Moulton, Paolo Pasquariello, Ali Reza, Richard Roll, Bernell Stone, René Stulz, Harry Turtle, Hao Wang, Xiaoyan Zhang, and for feedback from workshop participants at BYU, Cheung Kong, Cornell, Florida International, INSEAD, Laval, Rochester, SMU, UT Dallas, Tsinghua, Tulane, and the 2011 Australasian Banking and Finance Conference. -

Nber Working Paper Series Mean Reversion in Stock Prices: Evidence
NBER WORKING PAPER SERIES MEAN REVERSION IN STOCK PRICES: EVIDENCE AND IMPLICATIONS James M. Poterba Lawrence H. Summers Working Paper No. 2343 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 August 1987 We are grateful to Barry Peristein, Changyong Rhee, Jeff Zweibel and especially David Cutler for excellent research assistance, to Ben Bernanke, John Campbell, Robert Engle, Eugene Fama, Pete Kyle, Greg Mankiw, Julio Rotemberg, William Schwert, Kenneth Singleton, and Mark Watson for helpful comments, and to James Darcel, Matthew Shapiro, and Ian Tonks for data assistance. This research was supported by the National Science Foundation and was conducted while the first author was a Batterymarch Fellow. The research reported here is part of the NBERs research program in Financial Markets and Monetary Economics. Any opinions expressed are those of the authors and not those of the National Bureau of Economic Research. NBER Working Paper #2343 August 1987 Mean Reversion in Stock Prices: Evidence and Implications ABSTRACT This paper analyzes the statistical evidence bearing on whether transitory components account for a large fraction of the variance in common stock returns. The first part treats methodological issues involved in testing for transitory return components. It demonstrates that variance ratios are among the most powerful tests for detecting mean reversion in stock prices, but that they have little power against the principal interesting alternatives to the random walk hypothesis. The second part applies variance ratio tests to market returns for the United States over the 1871-1986 period and for seventeen other countries over the 1957-1985 period, as well as to returns on individual firms over the 1926- 1985 period. -
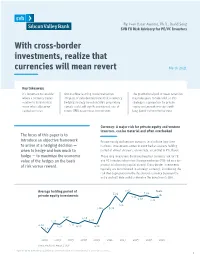
With Cross-Border Investments, Realize That Currencies Will Mean Revert March 2021
By: Ivan Oscar Asensio, Ph.D., David Song SVB FX Risk Advisory for PE/VC Investors With cross-border investments, realize that currencies will mean revert March 2021 Key takeaways It’s important to consider Our machine learning model trained on The gravitational pull of mean reversion where a currency trades 30 years of data demonstrates that a currency may take years to take hold, so this relative to its historical hedging strategy based on SVB’s proprietary strategy is appropriate for private mean when allocating signals could add significant internal rate of equity and growth investors with capital overseas. return (IRR) to overseas investments. long-dated investment horizons. Currency: A major risk for private equity and venture investors, can be material and often overlooked The focus of this paper is to introduce an objective framework Private equity and venture investors tend to have long time to arrive at a hedging decision — horizons. Investments exited in 2019 had an average holding when to hedge and how much to period of almost six years, on average, according to Pitchbook. hedge — to maximize the economic Those long investment durations heighten currency risk for PE value of the hedges on the basis and VC investors who inherit foreign exchange (FX) risk as a by- of risk versus reward. product of allocating capital abroad. Cross-border investments typically are denominated in a foreign currency1, introducing the risk that depreciation in the destination currency between the entry and exit date could undermine the investment’s IRR. 6.02 Years Average holding period of 5.84 5.82 5.76 private equity investments 5.91 5.80 5.75 5.47 5.04 5.31 4.52 4.45 4.33 4.27 4.34 4.07 4.23 4.29 4.26 3.77 2001 2003 2005 2007 2009 2011 2013 2015 2017 2019 Source: Pitchbook, August 1, 2019 1 Applies when both the acquisition and the exit price are denominated in a foreign currency.