Making Golden Cuts with a Shoemaker's Knife
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Arbelos in Wasan Geometry: Chiba's Problem
Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, Vol.8, (2019), Issue 2, pp.98-104 THE ARBELOS IN WASAN GEOMETRY: CHIBA’S PROBLEM HIROSHI OKUMURA Abstract. We consider a sangaku problem involving an arbelos with two congruent circles, and give several conditions where the two congruent circles appear. Also we show several pairs of congruent circles and Archimedean circles. 2010 Mathematical Subject Classification: 01A27, 51M04, 51N20. Keywords and phrases: arbelos, Archimedean circle, non-Archimedean congruent circles. 1. INTRODUCTION We consider the arbelos appeared in Wasan geometry, and consider an arbelos formed by three semicircles α, β and γ with diameters AO , BO and AB , respectively for a point O on the segment AB . The radii of α and β are denoted by a and b, respectively. We consider the following sangaku .(in 1880 [5] (see Figure 1 (نproblem proposed by Chiba ( ઍ༿ӫ࣏҆ δ ε γ α h β B O H A Figure 1. Problem 1. For a point H on the segment AO, let h be the perpendicular to AB at H. Let δ be the circle touching α and β externally and h, and let ε be the incircle of the curvilinear triangle made by α, γ and h. If δ and ε touch and δ is congruent to the circle of diameter AH, find the radius of ε in terms of a and b. Circles of radius rA = ab /(a + b) are said to be Archimedean. In this paper we generalize the problem and consider two circles touching at a point on a perpendicular to the line AB . -

Archimedes and the Arbelos1 Bobby Hanson October 17, 2007
Archimedes and the Arbelos1 Bobby Hanson October 17, 2007 The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics. — G.H. Hardy, A Mathematician’s Apology ACBr 1 − r Figure 1. The Arbelos Problem 1. We will warm up on an easy problem: Show that traveling from A to B along the big semicircle is the same distance as traveling from A to B by way of C along the two smaller semicircles. Proof. The arc from A to C has length πr/2. The arc from C to B has length π(1 − r)/2. The arc from A to B has length π/2. ˜ 1My notes are shamelessly stolen from notes by Tom Rike, of the Berkeley Math Circle available at http://mathcircle.berkeley.edu/BMC6/ps0506/ArbelosBMC.pdf . 1 2 If we draw the line tangent to the two smaller semicircles, it must be perpendicular to AB. (Why?) We will let D be the point where this line intersects the largest of the semicircles; X and Y will indicate the points of intersection with the line segments AD and BD with the two smaller semicircles respectively (see Figure 2). Finally, let P be the point where XY and CD intersect. D X P Y ACBr 1 − r Figure 2 Problem 2. Now show that XY and CD are the same length, and that they bisect each other. -

Solutions Manual to Accompany Classical Geometry
Solutions Manual to Accompany Classical Geometry Solutions Manual to Accompany CLASSICAL GEOMETRY Euclidean, Transformational, Inversive, and Projective I. E. Leonard J. E. Lewis A. C. F. Liu G. W. Tokarsky Department of Mathematical and Statistical Sciences University of Alberta Edmonton, Canada WILEY Copyright © 2014 by John Wiley & Sons, Inc. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representation or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. -

Chapter 6 the Arbelos
Chapter 6 The arbelos 6.1 Archimedes’ theorems on the arbelos Theorem 6.1 (Archimedes 1). The two circles touching CP on different sides and AC CB each touching two of the semicircles have equal diameters AB· . P W1 W2 A O1 O C O2 B A O1 O C O2 B Theorem 6.2 (Archimedes 2). The diameter of the circle tangent to all three semi- circles is AC CB AB · · . AC2 + AC CB + CB2 · We shall consider Theorem ?? in ?? later, and for now examine Archimedes’ wonderful proofs of the more remarkable§ Theorems 6.1 and 6.2. By synthetic reasoning, he computed the radii of these circles. 1Book of Lemmas, Proposition 5. 2Book of Lemmas, Proposition 6. 602 The arbelos 6.1.1 Archimedes’ proof of the twin circles theorem In the beginning of the Book of Lemmas, Archimedes has established a basic proposition 3 on parallel diameters of two tangent circles. If two circles are tangent to each other (internally or externally) at a point P , and if AB, XY are two parallel diameters of the circles, then the lines AX and BY intersect at P . D F I W1 E H W2 G A O C B Figure 6.1: Consider the circle tangent to CP at E, and to the semicircle on AC at G, to that on AB at F . If EH is the diameter through E, then AH and BE intersect at F . Also, AE and CH intersect at G. Let I be the intersection of AE with the outer semicircle. Extend AF and BI to intersect at D. -

Pappus of Alexandria: Book 4 of the Collection
Pappus of Alexandria: Book 4 of the Collection For other titles published in this series, go to http://www.springer.com/series/4142 Sources and Studies in the History of Mathematics and Physical Sciences Managing Editor J.Z. Buchwald Associate Editors J.L. Berggren and J. Lützen Advisory Board C. Fraser, T. Sauer, A. Shapiro Pappus of Alexandria: Book 4 of the Collection Edited With Translation and Commentary by Heike Sefrin-Weis Heike Sefrin-Weis Department of Philosophy University of South Carolina Columbia SC USA [email protected] Sources Managing Editor: Jed Z. Buchwald California Institute of Technology Division of the Humanities and Social Sciences MC 101–40 Pasadena, CA 91125 USA Associate Editors: J.L. Berggren Jesper Lützen Simon Fraser University University of Copenhagen Department of Mathematics Institute of Mathematics University Drive 8888 Universitetsparken 5 V5A 1S6 Burnaby, BC 2100 Koebenhaven Canada Denmark ISBN 978-1-84996-004-5 e-ISBN 978-1-84996-005-2 DOI 10.1007/978-1-84996-005-2 Springer London Dordrecht Heidelberg New York British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Library of Congress Control Number: 2009942260 Mathematics Classification Number (2010) 00A05, 00A30, 03A05, 01A05, 01A20, 01A85, 03-03, 51-03 and 97-03 © Springer-Verlag London Limited 2010 Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licenses issued by the Copyright Licensing Agency. -

REFLECTIONS on the ARBELOS Written in Block Capitals
REFLECTIONS ON THE ARBELOS HAROLD P. BOAS Written in block capitals on lined paper, the letter bore a postmark from a Northeastern seaport. \I have a problem that I would like to solve," the letter began, \but unfortunately I cannot. I dropped out from 2nd year high school, and this problem is too tough for me." There followed the diagram shown in Figure 1 along with the statement of the problem: to prove that the line segment DE has the same length as the line segment AB. Figure 1. A correspondent's hand-drawn puzzle \I tried this and went even to the library for information about mathematics," the letter continued, \but I have not succeeded. Would you be so kind to give me a full explanation?" Mindful of the romantic story [18] of G. H. Hardy's discovery of the Indian genius Ramanujan, a mathematician who receives such a letter wants ¯rst to rule out the remote possibility that the writer is some great unknown talent. Next, the question arises of whether the correspondent falls into the category of eccentrics whom Underwood Dudley terms mathematical cranks [14], for one ought not to encourage cranks. Date: October 26, 2004. This article is based on a lecture delivered at the nineteenth annual Rose-Hulman Undergraduate Mathematics Conference, March 15, 2002. 1 2 HAROLD P. BOAS Since this letter claimed no great discovery, but rather asked politely for help, I judged it to come from an enthusiastic mathematical am- ateur. Rather than ¯le such letters in the oubliette, or fob them o® on junior colleagues, I try to reply in a friendly way to communica- tions from coherent amateurs. -

Icons of Mathematics an EXPLORATION of TWENTY KEY IMAGES Claudi Alsina and Roger B
AMS / MAA DOLCIANI MATHEMATICAL EXPOSITIONS VOL 45 Icons of Mathematics AN EXPLORATION OF TWENTY KEY IMAGES Claudi Alsina and Roger B. Nelsen i i “MABK018-FM” — 2011/5/16 — 19:53 — page i — #1 i i 10.1090/dol/045 Icons of Mathematics An Exploration of Twenty Key Images i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page ii — #2 i i c 2011 by The Mathematical Association of America (Incorporated) Library of Congress Catalog Card Number 2011923441 Print ISBN 978-0-88385-352-8 Electronic ISBN 978-0-88385-986-5 Printed in the United States of America Current Printing (last digit): 10987654321 i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page iii — #3 i i The Dolciani Mathematical Expositions NUMBER FORTY-FIVE Icons of Mathematics An Exploration of Twenty Key Images Claudi Alsina Universitat Politecnica` de Catalunya Roger B. Nelsen Lewis & Clark College Published and Distributed by The Mathematical Association of America i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page iv — #4 i i DOLCIANI MATHEMATICAL EXPOSITIONS Committee on Books Frank Farris, Chair Dolciani Mathematical Expositions Editorial Board Underwood Dudley, Editor Jeremy S. Case Rosalie A. Dance Tevian Dray Thomas M. Halverson Patricia B. Humphrey Michael J. McAsey Michael J. Mossinghoff Jonathan Rogness Thomas Q. Sibley i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page v — #5 i i The DOLCIANI MATHEMATICAL EXPOSITIONS series of the Mathematical As- sociation of America was established through a generous gift to the Association from Mary P. -
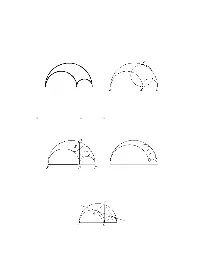
The Geometry of the Arbelos Brian Mortimer, Carleton University April, 1998
The Geometry of The Arbelos Brian Mortimer, Carleton University April, 1998 The basic figure of the arbelos (meaning “shoemaker’s knife”) is formed by three semicircles with diameters on the same line. Figure 1. The Shoemaker’s Knife Figure 2. Archimedes (died 212 BC) included several theorems about the arbelos in his “Book of Lemmas”. For example, in Figure 2, the area of the arbelos is equal to the area of the circle with diameter AD. The key is that AD2 = BD DC then expand BC2 = (BD + DC)2. · Another result is that, in Figure 3, the circles centred at E and F have the same radius. The two drawings of the figure illustrate how the theorem does not depend on the position of D on the base line. Figure 3. Another interesting elementary problem about the arbelos is to show (Figure 4) that, if A and C are the points of contact of the common tangent of the two inner circles then ABCD is a rectangle. See Stueve [12], for example. Figure 4. 1 Five centuries later, Pappus of Alexandria (circa 320 AD) gave a proof of the following remakable theorem about the arbelos. He claimed that it was known to the ancients but we now ascribe to Pappus himself. The rest of this paper is devoted to a proof of this result; the argument is developed from the proof presented by Heath [5] page 371. Theorem 1 If a chain of circles C1,C2,... is constructed inside an arbelos so that C1 is tangent to the three semicircles and Cn is tangent to two semi-circles and Cn 1 then, for all n, the height of the centre of − Cn above the base of the arbelos BC is n times the diameter of Cn. -

Simple Constructions of the Incircle of an Arbelos
Forum Geometricorum b Volume 1 (2001) 133–136. bbb FORUM GEOM ISSN 1534-1178 Simple Constructions of the Incircle of an Arbelos Peter Y. Woo Abstract. We give several simple constructions of the incircle of an arbelos, also known as a shoemaker’s knife. Archimedes, in his Book of Lemmas, studied the arbelos bounded by three semi- circles with diameters AB, AC, and CB, all on the same side of the diameters. 1 See Figure 1. Among other things, he determined the radius of the incircle of the arbelos. In Figure 2, GH is the diameter of the incircle parallel to the base AB, and G, H are the (orthogonal) projections of G, H on AB. Archimedes showed that GHHG is a square, and that AG, GH, HB are in geometric progression. See [1, pp. 307–308]. Z Z G Y X Y X H ABC ABG C H Figure 1 Figure 2 In this note we give several simple constructions of the incircle of the arbelos. The elegant Construction 1 below was given by Leon Bankoff [2]. The points of tangency are constructed by drawing circles with centers at the midpoints of two of the semicircles of the arbelos. In validating Bankoff’s construction, we obtain Constructions 2 and 3, which are easier in the sense that one is a ruler-only construction, and the other makes use only of the midpoint of one semicircle. Z Z Z Y Q Q ABX C P P Y X S Y X ABC ABC M Construction 1 Construction 2 Construction 3 Publication Date: September 18, 2001. -

Equilateral Triangles and Archimedean Circles Related to an Arbelos
Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, Vol.8, (2019), Issue 1, pp.1-11 EQUILATERAL TRIANGLES AND ARCHIMEDEAN CIRCLES RELATED TO AN ARBELOS NGUYEN NGOC GIANG AND LE VIET AN ABSTRACT . In this article, we construct the Archimedean circles from one or some equi- lateral triangles related to arbelos. And its converse, we also construct an another equi- lateral triangle from Yiu’s circle. 1. INTRODUCTION We consider an arbelos with greater semi-circle (O) of radius r and smaller semicircles (O1) and (O2) of radii r1 and r2 respectively. The semi-circles (O1) and (O) meet at A, (O2) and (O) at B, (O1) and (O2) at C. The line through C perpendicular to AB meets (O) at D, and (O′) is the Midway semi-circle with diameter O1O2, all on the same side r1r2 AB . Circles with radius t := r are called Archimedean. They are congruent to the Archimedean twin circles [1, 2]. We shall make use of the Yiu’s circle (that is the circle (A26 ) in [3], is also the circle (K3) in [4], or the circle touches γ internally, and touch α[1] and β[1] externally at Corollary 3 in [5]), with center Y (See figure 1). FIGURE 1. Yiu’s circle Key words and phrases. Arbelos, Archimedean circle, equilateral triangle, Yiu’s circle. AMS 2010 Mathematics Subject Classification:51M04. 1 N. G. Nguyen; V. A. Le Proposition 1.1. (Yiu [3] , [4] ). The circle (Y) tangent to both semi-circles (O) and (O′) and its center on CD is Archimedean. -

VARIATIONS on the ARBELOS 1. Introduction
Journal of Applied Mathematics and Computational Mechanics 2017, 16(2), 123-133 www.amcm.pcz.pl p-ISSN 2299-9965 DOI: 10.17512/jamcm.2017.2.10 e-ISSN 2353-0588 VARIATIONS ON THE ARBELOS Michał Różański, Alicja Samulewicz, Marcin Szweda, Roman Wituła Institute of Mathematics, Silesian University of Technology Gliwice, Poland [email protected], [email protected] [email protected], [email protected] Received: 12 April 2017; accepted: 18 May 2017 Abstract. We recall the ancient notion of arbelos and introduce a number of concepts gene- ralizing it. We follow the ideas presented by J. Sondow in his article on parbelos, the para- bolic analogue of the classic arbelos. Our concepts concern the curves constructed of arcs which resemble each other and surfaces obtained in a similar way. We pay special attention to ellarbelos, the curves built of semi-ellipses, because of their possible application in engi- neering, e.g. in determining the static moments of arc rod constructions or in problems of structural stability and durability of constructions. MSC 2010: 51N20, 51M25 Keywords: arbelos, parbelos, similarity, ellarbelos, F-arbelos 1. Introduction The starting point of this article was a discussion on the parabolic analogue of arbelos described in [1]. We tried to find other ways of generalizing this notion and we investigated the relationships between them. Since the issue was rather elemen- tary, the students had the opportunity to work on a par with more experienced mathematicians and all involved enjoyed this cooperation. Some of our interpreta- tions of the ancient subject are described in the following. -

Geometry Illuminated an Illustrated Introduction to Euclidean and Hyperbolic Plane Geometry
AMS / MAA TEXTBOOKS VOL 30 Geometry Illuminated An Illustrated Introduction to Euclidean and Hyperbolic Plane Geometry Matthew Harvey Geometry Illuminated An Illustrated Introduction to Euclidean and Hyperbolic Plane Geometry c 2015 by The Mathematical Association of America (Incorporated) Library of Congress Control Number: 2015936098 Print ISBN: 978-1-93951-211-6 Electronic ISBN: 978-1-61444-618-7 Printed in the United States of America Current Printing (last digit): 10987654321 10.1090/text/030 Geometry Illuminated An Illustrated Introduction to Euclidean and Hyperbolic Plane Geometry Matthew Harvey The University of Virginia’s College at Wise Published and distributed by The Mathematical Association of America Council on Publications and Communications Jennifer J. Quinn, Chair Committee on Books Fernando Gouvea,ˆ Chair MAA Textbooks Editorial Board Stanley E. Seltzer, Editor Matthias Beck Richard E. Bedient Otto Bretscher Heather Ann Dye Charles R. Hampton Suzanne Lynne Larson John Lorch Susan F. Pustejovsky MAA TEXTBOOKS Bridge to Abstract Mathematics, Ralph W. Oberste-Vorth, Aristides Mouzakitis, and Bonita A. Lawrence Calculus Deconstructed: A Second Course in First-Year Calculus, Zbigniew H. Nitecki Calculus for the Life Sciences: A Modeling Approach, James L. Cornette and Ralph A. Ackerman Combinatorics: A Guided Tour, David R. Mazur Combinatorics: A Problem Oriented Approach, Daniel A. Marcus Complex Numbers and Geometry, Liang-shin Hahn A Course in Mathematical Modeling, Douglas Mooney and Randall Swift Cryptological Mathematics, Robert Edward Lewand Differential Geometry and its Applications, John Oprea Distilling Ideas: An Introduction to Mathematical Thinking, Brian P.Katz and Michael Starbird Elementary Cryptanalysis, Abraham Sinkov Elementary Mathematical Models, Dan Kalman An Episodic History of Mathematics: Mathematical Culture Through Problem Solving, Steven G.