Smartee: a Neural Network Based Navigational Bot
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Openbsd Gaming Resource
OPENBSD GAMING RESOURCE A continually updated resource for playing video games on OpenBSD. Mr. Satterly Updated August 7, 2021 P11U17A3B8 III Title: OpenBSD Gaming Resource Author: Mr. Satterly Publisher: Mr. Satterly Date: Updated August 7, 2021 Copyright: Creative Commons Zero 1.0 Universal Email: [email protected] Website: https://MrSatterly.com/ Contents 1 Introduction1 2 Ways to play the games2 2.1 Base system........................ 2 2.2 Ports/Editors........................ 3 2.3 Ports/Emulators...................... 3 Arcade emulation..................... 4 Computer emulation................... 4 Game console emulation................. 4 Operating system emulation .............. 7 2.4 Ports/Games........................ 8 Game engines....................... 8 Interactive fiction..................... 9 2.5 Ports/Math......................... 10 2.6 Ports/Net.......................... 10 2.7 Ports/Shells ........................ 12 2.8 Ports/WWW ........................ 12 3 Notable games 14 3.1 Free games ........................ 14 A-I.............................. 14 J-R.............................. 22 S-Z.............................. 26 3.2 Non-free games...................... 31 4 Getting the games 33 4.1 Games............................ 33 5 Former ways to play games 37 6 What next? 38 Appendices 39 A Clones, models, and variants 39 Index 51 IV 1 Introduction I use this document to help organize my thoughts, files, and links on how to play games on OpenBSD. It helps me to remember what I have gone through while finding new games. The biggest reason to read or at least skim this document is because how can you search for something you do not know exists? I will show you ways to play games, what free and non-free games are available, and give links to help you get started on downloading them. -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae -

List of TCP and UDP Port Numbers from Wikipedia, the Free Encyclopedia
List of TCP and UDP port numbers From Wikipedia, the free encyclopedia This is a list of Internet socket port numbers used by protocols of the transport layer of the Internet Protocol Suite for the establishment of host-to-host connectivity. Originally, port numbers were used by the Network Control Program (NCP) in the ARPANET for which two ports were required for half- duplex transmission. Later, the Transmission Control Protocol (TCP) and the User Datagram Protocol (UDP) needed only one port for full- duplex, bidirectional traffic. The even-numbered ports were not used, and this resulted in some even numbers in the well-known port number /etc/services, a service name range being unassigned. The Stream Control Transmission Protocol database file on Unix-like operating (SCTP) and the Datagram Congestion Control Protocol (DCCP) also systems.[1][2][3][4] use port numbers. They usually use port numbers that match the services of the corresponding TCP or UDP implementation, if they exist. The Internet Assigned Numbers Authority (IANA) is responsible for maintaining the official assignments of port numbers for specific uses.[5] However, many unofficial uses of both well-known and registered port numbers occur in practice. Contents 1 Table legend 2 Well-known ports 3 Registered ports 4 Dynamic, private or ephemeral ports 5 See also 6 References 7 External links Table legend Official: Port is registered with IANA for the application.[5] Unofficial: Port is not registered with IANA for the application. Multiple use: Multiple applications are known to use this port. Well-known ports The port numbers in the range from 0 to 1023 are the well-known ports or system ports.[6] They are used by system processes that provide widely used types of network services. -

List of TCP and UDP Port Numbers 1 List of TCP and UDP Port Numbers
List of TCP and UDP port numbers 1 List of TCP and UDP port numbers This is a list of Internet socket port numbers used by protocols of the Transport Layer of the Internet Protocol Suite for the establishment of host-to-host communications. Originally, these ports number were used by the Transmission Control Protocol (TCP) and the User Datagram Protocol (UDP), but are also used for the Stream Control Transmission Protocol (SCTP), and the Datagram Congestion Control Protocol (DCCP). SCTP and DCCP services usually use a port number that matches the service of the corresponding TCP or UDP implementation if they exist. The Internet Assigned Numbers Authority (IANA) is responsible for maintaining the official assignments of port numbers for specific uses.[1] However, many unofficial uses of both well-known and registered port numbers occur in practice. Table legend Use Description Color Official Port is registered with IANA for the application white Unofficial Port is not registered with IANA for the application blue Multiple use Multiple applications are known to use this port. yellow Well-known ports The port numbers in the range from 0 to 1023 are the well-known ports. They are used by system processes that provide widely used types of network services. On Unix-like operating systems, a process must execute with superuser privileges to be able to bind a network socket to an IP address using one of the well-known ports. Port TCP UDP Description Status 0 UDP Reserved Official 1 TCP UDP TCP Port Service Multiplexer (TCPMUX) Official [2] [3] -

Fedora 16 Release Notes Release Notes for Fedora 16
Fedora 16 Release Notes Release Notes for Fedora 16 Edited by The Fedora Docs Team Copyright © 2011 Fedora Project Contributors. The text of and illustrations in this document are licensed by Red Hat under a Creative Commons Attribution–Share Alike 3.0 Unported license ("CC-BY-SA"). An explanation of CC-BY-SA is available at http://creativecommons.org/licenses/by-sa/3.0/. The original authors of this document, and Red Hat, designate the Fedora Project as the "Attribution Party" for purposes of CC-BY-SA. In accordance with CC-BY-SA, if you distribute this document or an adaptation of it, you must provide the URL for the original version. Red Hat, as the licensor of this document, waives the right to enforce, and agrees not to assert, Section 4d of CC-BY-SA to the fullest extent permitted by applicable law. Red Hat, Red Hat Enterprise Linux, the Shadowman logo, JBoss, MetaMatrix, Fedora, the Infinity Logo, and RHCE are trademarks of Red Hat, Inc., registered in the United States and other countries. For guidelines on the permitted uses of the Fedora trademarks, refer to https:// fedoraproject.org/wiki/Legal:Trademark_guidelines. Linux® is the registered trademark of Linus Torvalds in the United States and other countries. Java® is a registered trademark of Oracle and/or its affiliates. XFS® is a trademark of Silicon Graphics International Corp. or its subsidiaries in the United States and/or other countries. MySQL® is a registered trademark of MySQL AB in the United States, the European Union and other countries. All other trademarks are the property of their respective owners. -

Prologin System Administration's Documentation!
Prologin System Administration Release 2020 Association Prologin Aug 18, 2020 CONTENTS 1 Infrastructure overview 3 1.1 Documentation maintainers ........................................ 3 1.2 Requirements ............................................... 3 1.3 Network infrastructure .......................................... 4 1.4 Machine database ............................................. 4 1.5 User database ............................................... 5 1.6 File storage ................................................ 5 1.7 Other small services ........................................... 6 2 Setup instructions 7 2.1 Step 0: Hardware and network setup ................................... 7 2.2 Step 1: Writing the Ansible inventory .................................. 8 2.3 Step 2: Setting up the gateway ...................................... 8 2.3.1 File system setup ........................................ 8 2.3.2 SADM deployment ....................................... 9 2.3.3 Gateway network configuration ................................. 10 2.4 Step 3: File storage ............................................ 10 2.4.1 RHFS Inventory setup ...................................... 11 2.4.2 Installing the RHFS ....................................... 11 2.4.3 Registering the switches ..................................... 11 2.5 Step 4: Booting the user machines .................................... 12 2.6 Step 5: Installing the service machines .................................. 12 2.7 Note: Testing on qemu/libvirt ..................................... -

Technical Notes All Changes in Fedora 13
Fedora 13 Technical Notes All changes in Fedora 13 Edited by The Fedora Docs Team Copyright © 2010 Red Hat, Inc. and others. The text of and illustrations in this document are licensed by Red Hat under a Creative Commons Attribution–Share Alike 3.0 Unported license ("CC-BY-SA"). An explanation of CC-BY-SA is available at http://creativecommons.org/licenses/by-sa/3.0/. The original authors of this document, and Red Hat, designate the Fedora Project as the "Attribution Party" for purposes of CC-BY-SA. In accordance with CC-BY-SA, if you distribute this document or an adaptation of it, you must provide the URL for the original version. Red Hat, as the licensor of this document, waives the right to enforce, and agrees not to assert, Section 4d of CC-BY-SA to the fullest extent permitted by applicable law. Red Hat, Red Hat Enterprise Linux, the Shadowman logo, JBoss, MetaMatrix, Fedora, the Infinity Logo, and RHCE are trademarks of Red Hat, Inc., registered in the United States and other countries. For guidelines on the permitted uses of the Fedora trademarks, refer to https:// fedoraproject.org/wiki/Legal:Trademark_guidelines. Linux® is the registered trademark of Linus Torvalds in the United States and other countries. Java® is a registered trademark of Oracle and/or its affiliates. XFS® is a trademark of Silicon Graphics International Corp. or its subsidiaries in the United States and/or other countries. All other trademarks are the property of their respective owners. Abstract This document lists all changed packages between Fedora 12 and Fedora 13. -
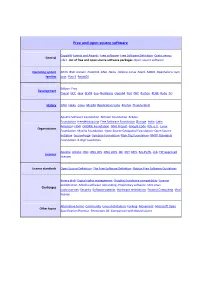
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed -

Pardus-Linux.Org Edergi 19. Sayı
gunluk. lkd. org. tr'den alınmıştır. İçindekiler Giriş Yazısı 3 Başla ve Oyna! : Linux-Gamers 4 Wesnoth'a Dalış III 15 Pardus'ta Scilab II 24 Pardus'ta Django 27 Makale: Microsoft'un Rehberliğinde Teknoloji Geliştirmek 31 Makale: Yaratıcılık ve Özgür Düşünce Üzerine 32 Röportaj: Alexandre Julliard (Wine) 35 Torrentlerinizi Uzaktan Yönetin 39 2 Giriş Yazısı Erdem Artan Merhaba Özgür Yazılım Dostları, ben Erdem Artan Wine projesinin lideri kaçarlar evlerine Alexandre Julliard ile yaptığım röportajı ve onlar ki bir nice mürtede hançer üşürürler Mayıs ayı.. İşçilerin özgürce Taksim' ve uzaktan torrent yönetimini sizler için ve yeşil bir ağaç gibi gülen de bayramlarını kutlayabildikleri hazırladık. ve merasimsiz ağlayan Mayıs ayı... Linux Kullanıcıları Derneği' ve ana avrat küfreden ki onlardır, nin "Özgür Bir Dünya İçin Özgür Ya- Beğeneceğinizi umduğum sayıyı size destanımızda yalnız onların maceraları vardır. zılım" pankartıyla korteje katıldığı Ma- sunarken Annelerimizin Anneler Günü- yıs ayı... Fidanların yeşerdiği veya nü ve İşçi Kardeşlerimizin geçmiş bay- Demir, yeşermesi gerektiği Mayıs ayı... Hepi- ramlarını kutlar, sizleri Nazım Hikmet'in kömür mizin en büyük varlığı olan, olması ge- "Onlar" adlı şiiri ile başbaşa bırakıyo- ve şeker reken, dünyadaki tüm güzellikleri hak e- rum. ve kırmızı bakır den annelerimiz için düşünülen ufa- ve mensucat cık, tepecik, bir dolu fıçıcık gününü Bu arada TruvaLinux 6 yılı devirmiş. ve sevda ve zulüm ve hayat barındıran Mayıs ayı... Mutlu yıllar dilerim. ve bilcümle sanayi kollarının ve gökyüzü Ve Pardus Kullanıcıları Derneği hizmet- Onlar ki toprakta karınca, ve sahra lerinden olan Pardus-Linux.Org Toplulu- suda balık, ve mavi okyanus ğu tarafından hazırlan Pardus-Linux.Org havada kuş kadar ve kederli nehir yollarının, eDergi (Pardus eDergi)'nin 19. -

Why Do Users Choose Open Source Software? Analysis of the Network Effect
Working Papers No. 5/2015 (153) DOROTA CELIŃSKA MIROSŁAWA LASEK Why do users choose Open Source software? Analysis of the network effect Warsaw 2015 Why do users choose Open Source software? Analysis of the network effect DOROTA CELIŃSKA MIROSŁAWA LASEK Faculty of Economic Sciences (post mortem) University of Warsaw Faculty of Economic Sciences e-mail: dcelinska @wne.uw.edu.pl University of Warsaw Abstract This article analyses the phenomenon of using the Open Source software. Its aim is to verify the existence of a positive direct network effect that characterizes using of the Open Source software. The multivariate probit model is used to extract factors motivating users to the usage of the Open Source software. Special attention is paid to demographic characteristics of users, as well as to the impact of users' acquaintances, such as family, work and school on using the Open Source software. The results of the conducted analysis confirm our research. Keywords: Open Source, software, source code, end user characteristics, network effect, multivariate probit, motivation JEL: L17, 86, L C38, D12 Working Papers contain preliminary research results. Please consider this when citing the paper. Please contact the authors to give comments or to obtain revised version. Any mistakes and the views expressed herein are solely those of the authors. Introduction The Open Source software constitutes a software class with publicly accessible source code that can be modified by users. In recent years a rapid growth in the number of organizations that choose the Open Source licenses for their products is noticed. Even enterprises associated with typically commercial activities, such as Samsung, Google or Microsoft, tend to release large amounts of code for the needs of Open Source projects. -

Load Generation for Investigating Game System Scalability from Demands to Tools Stig Magnus Halvorsen Master’S Thesis Autumn 2014
Load Generation for Investigating Game System Scalability from Demands to Tools Stig Magnus Halvorsen Master’s Thesis Autumn 2014 Load Generation for Investigating Game System Scalability Stig Magnus Halvorsen June 26, 2014 “This book is dedicated to anyone and everyone who under- stands that hacking and learning is a way to live your life, not a day job or a semi-ordered list of instructions found in a thick book.” — Chris Anley, John Heasman, Felix “FX” Linder, and Gerardo Richarte [2, p. v] ii Abstract Video games have proven to be an interesting platform for computer scientists, as many games demand the latest technology, fast response times and effective utilization of hardware. Video games have been used both as a topic of and a tool for computer science (CS). Finding the right games to perform experiments on is however difficult. An important reason is the lack of suitable games for research. Open source games are attractive candidates as their availability and openness is crucial to provide reproducible research. Because researchers lack access to source code of commercial games, some create their own smaller prototype games to test their ideas without performing tests in large-scale productions. This decreases the practical applicability of their conclusion. The first major contribution of the thesis is a comparative study of available open source games. A survey shows a list of demands that can be used to evaluate if a game is applicable for academic use. The study unveils that no open source game projects of commercial quality are available. Still, some open source games seem useful for research. -

Star Wars Pack Gmod
Star wars pack gmod click here to download I try to keep this pack updated all the time so it includes all worthwhile Star Wars addons on the Steam Workshop for Gmod. It includes work of. Steam Workshop: Garry's Mod. This is a Star Wars: The Clone Wars collection pack, this content pack contains addons focused on the Clone. I'm done with gmod and I don't take requests, so please stop spamming the comment section. There won't be any updates or new packs. Steam Workshop: Garry's Mod. Star wars RP A small pack of Star Wars playermodels made for the Refugee Gamers servers. Includes. Steam Workshop: Garry's Mod. A collection of gmod star wars addons. Star Wars weapons pack (ragdolls) PS:Write to me in my profile link to. This is a content pack designed for the Garry's Mod Gamemode CW: Clone Wars, a roleplaying gamemode based in the STAR WARS universe. Free Starwars downloads for Garry's Mod - download Starwars for GMod for free. Dansnpc Pack FULL. Submitted by www.doorway.ru Star wars NPCs Sweps. These are the best mods I have seen for Star wars on Gmod. Mods In Video Remember they are in a Pack. (Garry's Mod) is a video in which Venturian and BethanyFrye play Garry's Mod with the Star Wars Battlefront weapons mod pack on the Mustafar map. Star Wars Mini Pack: A Other/Misc Garry's Mod (GMOD) Skin Mod submitted by The Master MLG/Elcastigador HI THIS S THE STAR WARS PACK FROM MATT WILD IT TREPEUIRES GMOD PLEASE INTSALL IN YOUR ADDONS DIRECTORY.