An IDL Graphical User Interface for Exoplanet Transit Photometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star. -

The Extragalactic Distance Scale
The Extragalactic Distance Scale Published in "Stellar astrophysics for the local group" : VIII Canary Islands Winter School of Astrophysics. Edited by A. Aparicio, A. Herrero, and F. Sanchez. Cambridge ; New York : Cambridge University Press, 1998 Calibration of the Extragalactic Distance Scale By BARRY F. MADORE1, WENDY L. FREEDMAN2 1NASA/IPAC Extragalactic Database, Infrared Processing & Analysis Center, California Institute of Technology, Jet Propulsion Laboratory, Pasadena, CA 91125, USA 2Observatories, Carnegie Institution of Washington, 813 Santa Barbara St., Pasadena CA 91101, USA The calibration and use of Cepheids as primary distance indicators is reviewed in the context of the extragalactic distance scale. Comparison is made with the independently calibrated Population II distance scale and found to be consistent at the 10% level. The combined use of ground-based facilities and the Hubble Space Telescope now allow for the application of the Cepheid Period-Luminosity relation out to distances in excess of 20 Mpc. Calibration of secondary distance indicators and the direct determination of distances to galaxies in the field as well as in the Virgo and Fornax clusters allows for multiple paths to the determination of the absolute rate of the expansion of the Universe parameterized by the Hubble constant. At this point in the reduction and analysis of Key Project galaxies H0 = 72km/ sec/Mpc ± 2 (random) ± 12 [systematic]. Table of Contents INTRODUCTION TO THE LECTURES CEPHEIDS BRIEF SUMMARY OF THE OBSERVED PROPERTIES OF CEPHEID -
Not Surprising That the Method Begins to Break Down at This Point
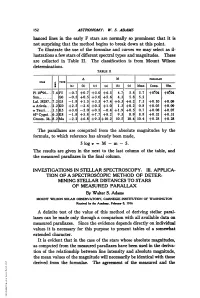
152 ASTRONOMY: W. S. ADAMS hanced lines in the early F stars are normally so prominent that it is not surprising that the method begins to break down at this point. To illustrate the use of the formulae and curves we may select as il- lustrations a few stars of different spectral types and magnitudes. These are collected in Table II. The classification is from Mount Wilson determinations. TABLE H ~A M PARAIuAX srTATYP_________________ (a) I(b) (C) (a) (b) c) Mean Comp. Ob. Pi 10U96.... 7.6F5 -0.7 +0.7 +3.0 +6.5 4.7 5.8 5.7 +0#04 +0.04 Sun........ GO -0.5 +0.5 +3.0 +5.6 4.3 5.8 5.2 Lal. 38287.. 7.2 G5 -1.8 +1.5 +3.5 +7.4 +6.3 +6.2 7.3 +0.10 +0.09 a Arietis... 2.2K0O +2.5 -2.4 +0.2 +1.0 1.3 +0.2 0.8 +0.05 +0.09 aTauri.... 1.1K5 +3.0 -2.0 +0.5 -0.4 +1.9 +0.5 0.7 +0.08 +0.07 61' Cygni...6.3K8 -1.8 +5.8 +7.7 +8.2 9.3 8.9 8.8 +0.32 +0.31 Groom. 34..8.2 Ma -2.2 +6.8 +9.2 +10.2 10.5 10.4 10.4 +0.28 +0.28 The parallaxes are computed from the absolute magnitudes by the formula, to which reference has already been made, 5 logr = M - m - 5. The results are given in the next to the last column of the table, and the measured parallaxes in the final column. -

Jason A. Dittmann 51 Pegasi B Postdoctoral Fellow
Jason A. Dittmann 51 Pegasi b Postdoctoral Fellow Contact Massachusetts Institute of Technology MIT Kavli Institute: 37-438f 617-258-5928 (office) 70 Vassar St. 520-820-0928 (cell) Cambridge, MA 02139 [email protected] Education Harvard University, Cambridge, MA PhD, Astronomy and Astrophysics, May 2016 Advisor: David Charbonneau, PhD • University of Arizona, Tucson, AZ BS, Astronomy, Physics, May 2010 Advisor: Laird Close, PhD • Recent 51 Pegasi b Postdoctoral Fellow July 2017 – Present Research Earth and Planetary Science Department, MIT Positions Faculty Contact: Sara Seager Postdoctoral Researcher Feb 2017 – June 2017 Kavli Institute, MIT Supervisor: Sarah Ballard Postdoctoral Researcher July 2016 – Jan 2017 Center for Astrophysics, Harvard University Supervisor: David Charbonneau Research Assistant Sep 2010 – May 2016 Center for Astrophysics, Harvard University Advisors: David Charbonneau Publication 16 first and second authored publications Summary 22 additional co-authored publications 1 first-authored publication in Nature 1 co-authored publication in Nature Selected 51 Pegasi b Postdoctoral Fellowship 2017 – Present Awards and Pierce Fellowship 2010 – 2013 Honors Certificate of Distinction in Teaching 2012 Best Project Award, Physics Ugrd. Research Symp. 2009 Best Undergraduate Research (Steward Observatory) 2009 – 2010 Grants Principal Investigator, Hubble Space Telescope 2017, 10 orbits Awarded “Initial Reconaissance of a Transiting Rocky (maximum award) Planet in a Nearby M-Dwarf’s Habitable Zone” Principal Investigator, -

Binocular Double Star Logbook
Astronomical League Binocular Double Star Club Logbook 1 Table of Contents Alpha Cassiopeiae 3 14 Canis Minoris Sh 251 (Oph) Psi 1 Piscium* F Hydrae Psi 1 & 2 Draconis* 37 Ceti Iota Cancri* 10 Σ2273 (Dra) Phi Cassiopeiae 27 Hydrae 40 & 41 Draconis* 93 (Rho) & 94 Piscium Tau 1 Hydrae 67 Ophiuchi 17 Chi Ceti 35 & 36 (Zeta) Leonis 39 Draconis 56 Andromedae 4 42 Leonis Minoris Epsilon 1 & 2 Lyrae* (U) 14 Arietis Σ1474 (Hya) Zeta 1 & 2 Lyrae* 59 Andromedae Alpha Ursae Majoris 11 Beta Lyrae* 15 Trianguli Delta Leonis Delta 1 & 2 Lyrae 33 Arietis 83 Leonis Theta Serpentis* 18 19 Tauri Tau Leonis 15 Aquilae 21 & 22 Tauri 5 93 Leonis OΣΣ178 (Aql) Eta Tauri 65 Ursae Majoris 28 Aquilae Phi Tauri 67 Ursae Majoris 12 6 (Alpha) & 8 Vul 62 Tauri 12 Comae Berenices Beta Cygni* Kappa 1 & 2 Tauri 17 Comae Berenices Epsilon Sagittae 19 Theta 1 & 2 Tauri 5 (Kappa) & 6 Draconis 54 Sagittarii 57 Persei 6 32 Camelopardalis* 16 Cygni 88 Tauri Σ1740 (Vir) 57 Aquilae Sigma 1 & 2 Tauri 79 (Zeta) & 80 Ursae Maj* 13 15 Sagittae Tau Tauri 70 Virginis Theta Sagittae 62 Eridani Iota Bootis* O1 (30 & 31) Cyg* 20 Beta Camelopardalis Σ1850 (Boo) 29 Cygni 11 & 12 Camelopardalis 7 Alpha Librae* Alpha 1 & 2 Capricorni* Delta Orionis* Delta Bootis* Beta 1 & 2 Capricorni* 42 & 45 Orionis Mu 1 & 2 Bootis* 14 75 Draconis Theta 2 Orionis* Omega 1 & 2 Scorpii Rho Capricorni Gamma Leporis* Kappa Herculis Omicron Capricorni 21 35 Camelopardalis ?? Nu Scorpii S 752 (Delphinus) 5 Lyncis 8 Nu 1 & 2 Coronae Borealis 48 Cygni Nu Geminorum Rho Ophiuchi 61 Cygni* 20 Geminorum 16 & 17 Draconis* 15 5 (Gamma) & 6 Equulei Zeta Geminorum 36 & 37 Herculis 79 Cygni h 3945 (CMa) Mu 1 & 2 Scorpii Mu Cygni 22 19 Lyncis* Zeta 1 & 2 Scorpii Epsilon Pegasi* Eta Canis Majoris 9 Σ133 (Her) Pi 1 & 2 Pegasi Δ 47 (CMa) 36 Ophiuchi* 33 Pegasi 64 & 65 Geminorum Nu 1 & 2 Draconis* 16 35 Pegasi Knt 4 (Pup) 53 Ophiuchi Delta Cephei* (U) The 28 stars with asterisks are also required for the regular AL Double Star Club. -

IAU Division C Working Group on Star Names 2019 Annual Report
IAU Division C Working Group on Star Names 2019 Annual Report Eric Mamajek (chair, USA) WG Members: Juan Antonio Belmote Avilés (Spain), Sze-leung Cheung (Thailand), Beatriz García (Argentina), Steven Gullberg (USA), Duane Hamacher (Australia), Susanne M. Hoffmann (Germany), Alejandro López (Argentina), Javier Mejuto (Honduras), Thierry Montmerle (France), Jay Pasachoff (USA), Ian Ridpath (UK), Clive Ruggles (UK), B.S. Shylaja (India), Robert van Gent (Netherlands), Hitoshi Yamaoka (Japan) WG Associates: Danielle Adams (USA), Yunli Shi (China), Doris Vickers (Austria) WGSN Website: https://www.iau.org/science/scientific_bodies/working_groups/280/ WGSN Email: [email protected] The Working Group on Star Names (WGSN) consists of an international group of astronomers with expertise in stellar astronomy, astronomical history, and cultural astronomy who research and catalog proper names for stars for use by the international astronomical community, and also to aid the recognition and preservation of intangible astronomical heritage. The Terms of Reference and membership for WG Star Names (WGSN) are provided at the IAU website: https://www.iau.org/science/scientific_bodies/working_groups/280/. WGSN was re-proposed to Division C and was approved in April 2019 as a functional WG whose scope extends beyond the normal 3-year cycle of IAU working groups. The WGSN was specifically called out on p. 22 of IAU Strategic Plan 2020-2030: “The IAU serves as the internationally recognised authority for assigning designations to celestial bodies and their surface features. To do so, the IAU has a number of Working Groups on various topics, most notably on the nomenclature of small bodies in the Solar System and planetary systems under Division F and on Star Names under Division C.” WGSN continues its long term activity of researching cultural astronomy literature for star names, and researching etymologies with the goal of adding this information to the WGSN’s online materials. -

CIRCULAR No. 170 (FEBRUARY 2010)
INTERNATIONAL ASTRONOMICAL UNION COMMISSION 26 (DOUBLE STARS) INFORMATION CIRCULAR No. 170 (FEBRUARY 2010) NEW ORBITS ADS Name P T e (2000) 2010 Author(s) ®2000± n a i ! Last ob. 2011 111 BU 391 AB 616y04 2095.68 0.103 81±75 259±0 100352 ZIRM 00094-2759 0±5925 100500 98±98 256±86 2006.940 258.9 1.346 - SEE3 406.00 1978.45 0.850 267.70 117.00 0.801 HARTKOPF 00098-3347 0.8871 1.119 41.7 77.6 2008.5490 117.70 0.814 & MASON - HDS 33 29.03 2018.12 0.378 177.0 132.0 0.189 CVETKOVIC 00143-2732 12.4010 0.251 59.8 73.9 2008.5432 141.6 0.199 - B 1024 1466. 1926.38 0.814 126.0 73.1 0.410 LING 00149-3209 0.2456 1.586 110.4 311.8 2008.5431 72.3 0.410 238 A1803AB 35.66 1950.70 0.002 124.10 306.00 0.179 HARTKOPF 00174+0853 10.0950 0.189 95.4 282.0 2008.7670 305.00 0.187 & MASON 281 BU1015 137.00 1961.65 0.557 291.20 103.80 0.483 HARTKOPF 00206+1219 2.6283 0.333 35.0 10.0 2008.8879 104.70 0.487 & MASON - HDS 56 28.05 1999.30 0.481 96.1 294.0 0.326 CVETKOVIC 00251+4803 12.8323 0.230 164.0 358.9 2007.8257 288.7 0.334 - B1909 11.35 1995.09 0.005 119.49 311.90 0.175 HARTKOPF 00284-2020 31.7093 0.202 69.8 99.0 2009.6710 334.80 0.109 & MASON 475 D2AB 2981.00 2007.00 0.923 266.00 42.80 0.067 HARTKOPF 00345-0433 0.1208 2.740 77.5 80.2 2009.7560 55.40 0.090 & MASON 520 BU395 25.02 1998.78 0.218 291.98 96.70 0.496 HARTKOPF 00373-2446 14.3905 0.675 78.6 318.1 2009.7560 101.00 0.596 & MASON - I440 196.00 2142.00 0.650 57.00 269.30 0.402 HARTKOPF 00427-6537 1.8350 0.274 157.0 344.0 2009.6710 268.70 0.405 & MASON 1 NEW ORBITS (continuation) ADS Name P T e (2000) 2010 Author(s) ®2000± n a i ! Last ob. -

Annual Report / Rapport Annuel / Jahresbericht 1996
Annual Report / Rapport annuel / Jahresbericht 1996 ✦ ✦ ✦ E U R O P E A N S O U T H E R N O B S E R V A T O R Y ES O✦ 99 COVER COUVERTURE UMSCHLAG Beta Pictoris, as observed in scattered light Beta Pictoris, observée en lumière diffusée Beta Pictoris, im Streulicht bei 1,25 µm (J- at 1.25 microns (J band) with the ESO à 1,25 microns (bande J) avec le système Band) beobachtet mit dem adaptiven opti- ADONIS adaptive optics system at the 3.6-m d’optique adaptative de l’ESO, ADONIS, au schen System ADONIS am ESO-3,6-m-Tele- telescope and the Observatoire de Grenoble télescope de 3,60 m et le coronographe de skop und dem Koronographen des Obser- coronograph. l’observatoire de Grenoble. vatoriums von Grenoble. The combination of high angular resolution La combinaison de haute résolution angu- Die Kombination von hoher Winkelauflö- (0.12 arcsec) and high dynamical range laire (0,12 arcsec) et de gamme dynamique sung (0,12 Bogensekunden) und hohem dy- (105) allows to image the disk to only 24 AU élevée (105) permet de reproduire le disque namischen Bereich (105) erlaubt es, die from the star. Inside 50 AU, the main plane jusqu’à seulement 24 UA de l’étoile. A Scheibe bis zu einem Abstand von nur 24 AE of the disk is inclined with respect to the l’intérieur de 50 UA, le plan principal du vom Stern abzubilden. Innerhalb von 50 AE outer part. Observers: J.-L. Beuzit, A.-M. -

Exoplanet Overview
Exoplanet Properties, System Architectures and Host Stars John Asher Johnson Caltech Department of Astronomy What we knew in 1994 • Planets form in disks – Planets orbit in same direction as stellar spin, and in same direction as other planets. • Giant planets have circular orbits • Giant planets reside near where they formed, beyond the “iceline” • Giant planets have a ~10 MEarth core surrounded by a gaseous envelope What We Expected Rocky planets Gas giants far away in close High-Precision Radial Velocities 95% of known exoplanets have been discovered or confirmed by Doppler measurements Jupiter’s Doppler Signal Orbit Period Planet Mass Meters per second What We Found 4.2 days! 0.45 Jupiter masses Meters per second 51 Pegasi Ensemble Johnson 2009 Mass ecc 1.5 ms^-1 10-3 pixel Johnson, Butler et al. 2006 Low-mass planets Howard, Johnson, Marcy et al. 2009 OGLE-2005-BLG-390b Beaulieu et al. 2008 MP = 5.5 Mearth a = 2.6 AU 28% of apparently single-planet systems Multiplanetturn Systems out to have additional Are planets Common Wright et al. 2009 Hot Jupiters: A Problem and an Opportunity Hot Jupiters The Problem of Forming Hot Jupiters The “Ice Line” in situ formation unlikely Figure courtesy of Transit Demo Josh Winn Inclination: MP rather than MPsini 2 (RP/R*) : Radius Relative brightness Time The HATNet Planet Search Hungarian-made Automated Telescope Doppler measurements needed to confirm transiting planets Johnson, Winn, Cabrera, Carter (2009) WASP-10 Actual WASP-10 RP = 1.06 RJup Precision: 0.5 mmag precision UH 2.2m + OPTIC Mass-Radius Torres, Winn, Holman 2008 Weird interiors Knutson et al. -

Exoplanet Detection Techniques
Exoplanet Detection Techniques Debra A. Fischer1, Andrew W. Howard2, Greg P. Laughlin3, Bruce Macintosh4, Suvrath Mahadevan5;6, Johannes Sahlmann7, Jennifer C. Yee8 We are still in the early days of exoplanet discovery. Astronomers are beginning to model the atmospheres and interiors of exoplanets and have developed a deeper understanding of processes of planet formation and evolution. However, we have yet to map out the full complexity of multi-planet architectures or to detect Earth analogues around nearby stars. Reaching these ambitious goals will require further improvements in instru- mentation and new analysis tools. In this chapter, we provide an overview of five observational techniques that are currently employed in the detection of exoplanets: optical and IR Doppler measurements, transit pho- tometry, direct imaging, microlensing, and astrometry. We provide a basic description of how each of these techniques works and discuss forefront developments that will result in new discoveries. We also highlight the observational limitations and synergies of each method and their connections to future space missions. Subject headings: 1. Introduction tary; in practice, they are not generally applied to the same sample of stars, so our detection of exoplanet architectures Humans have long wondered whether other solar sys- has been piecemeal. The explored parameter space of ex- tems exist around the billions of stars in our galaxy. In the oplanet systems is a patchwork quilt that still has several past two decades, we have progressed from a sample of one missing squares. to a collection of hundreds of exoplanetary systems. Instead of an orderly solar nebula model, we now realize that chaos 2. -

Analysis of New High-Precision Transit Light Curves of WASP-10 B: Starspot Occultations, Small Planetary Radius, and High Metallicity�,
A&A 535, A7 (2011) Astronomy DOI: 10.1051/0004-6361/201117127 & c ESO 2011 Astrophysics Analysis of new high-precision transit light curves of WASP-10 b: starspot occultations, small planetary radius, and high metallicity, G. Maciejewski1,2, St. Raetz2, N. Nettelmann3, M. Seeliger2,C.Adam2,G.Nowak1, and R. Neuhäuser2 1 Torun´ Centre for Astronomy, Nicolaus Copernicus University, Gagarina 11, 87100 Torun,´ Poland e-mail: [email protected] 2 Astrophysikalisches Institut und Universitäts-Sternwarte, Schillergässchen 2–3, 07745 Jena, Germany 3 Institut für Physik, Universität Rostock, 18051 Rostock, Germany Received 22 April 2011 / Accepted 5 September 2011 ABSTRACT Context. The WASP-10 planetary system is intriguing because different values of radius have been reported for its transiting exoplanet. The host star exhibits activity in terms of photometric variability, which is caused by the rotational modulation of the spots. Moreover, a periodic modulation has been discovered in transit timing of WASP-10 b, which could be a sign of an additional body perturbing the orbital motion of the transiting planet. Aims. We attempt to refine the physical parameters of the system, in particular the planetary radius, which is crucial for studying the internal structure of the transiting planet. We also determine new mid-transit times to confirm or refute observed anomalies in transit timing. Methods. We acquired high-precision light curves for four transits of WASP-10 b in 2010. Assuming various limb-darkening laws, we generated best-fit models and redetermined parameters of the system. The prayer-bead method and Monte Carlo simulations were used to derive error estimates. -

Abstract Ems
abstracts.md A table containing the talk and poster abstracts is posted below, in alphabetical order of last name. The posters themselves can be viewed on ZENODO (click for link), as well as during the gather.town live viewing sessions. Poster identifiers are in a topic.idnumber schema. Categories are as follows: 1. Atmospheres and Interiors . Detection: Transits, RVs, Microlensing, Astrometry, Imaging . Planet Formation (+ Disk) + Evolution . Know Your Star . Population Statistics & Occurrence . Dynamics 3. Instrumentation / Future 4. Habitability & Astrobiology 5. Machine Learning / Techniques / Methods Name (Affiliation). Title. Abstract Where. We present the optical transmission spectrum of the highly inflated Saturn-mass exoplanet WASP- 21b, using three transits obtained with the ACAM instrument on the William Herschel Telescope through the LRG-BEASTS survey (Low Resolution Ground-Based Exoplanet Atmosphere Survey Lili Alderson (University of using Transmission Spectroscopy). Our transmission spectrum covers a wavelength range of 4635- Bristol). LRG-BEASTS: 9000Å, achieving an average transit depth precision of 197ppm compared to one atmospheric scale Ground-bAsed Detection height at 246ppm. Whilst we detect sodium absorption in a bin width of 30Å, at >4 sigma of Sodium And A Steep confidence, we see no evidence of absorption from potassium. Atmospheric retrieval analysis of the OpticAl Slope in the scattering slope indicates that it is too steep for Rayleigh scattering from H2, but is very similar to Atmosphere of the Highly that of HD189733b. The features observed in our transmission spectrum cannot be caused by stellar InflAted Hot-SAturn activity alone, with photometric monitoring and Ca H&K analysis of WASP-21 showing it to be an WASP-21b.