University Physics Volume 3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
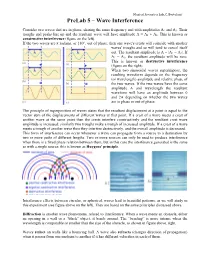
Prelab 5 – Wave Interference
Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths. -

Capacitance and Dielectrics
Chapter 24 Capacitance and Dielectrics PowerPoint® Lectures for University Physics, Twelfth Edition – Hugh D. Young and Roger A. Freedman Lectures by James Pazun Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley Goals for Chapter 24 • To consider capacitors and capacitance • To study the use of capacitors in series and capacitors in parallel • To determine the energy in a capacitor • To examine dielectrics and see how different dielectrics lead to differences in capacitance Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley How to Accomplish these goals: Read the chapter Study this PowerPoint Presentation Do the homework: 11, 13, 15, 39, 41, 45, 71 Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley Introduction • When flash devices made the “big switch” from bulbs and flashcubes to early designs of electronic flash devices, you could use a camera and actually hear a high-pitched whine as the “flash charged up” for your next photo opportunity. • The person in the picture must have done something worthy of a picture. Just think of all those electrons moving on camera flash capacitors! Copyright © 2008 Pearson Education Inc., publishing as Pearson Addison-Wesley Keep charges apart and you get capacitance Any two charges insulated from each other form a capacitor. When we say that a capacitor has a charge Q or that charge Q is stored in the capacitor, we mean that the conductor at higher potential has charge +Q and at lower potential has charge –Q. When the capacitor is fully charged the potential difference across it is the same as the vab that charged it. -

Quantum Interference Experiments with Large Molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger
Quantum interference experiments with large molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger Citation: American Journal of Physics 71, 319 (2003); doi: 10.1119/1.1531580 View online: http://dx.doi.org/10.1119/1.1531580 View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/71/4?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Quantum interference and control of the optical response in quantum dot molecules Appl. Phys. Lett. 103, 222101 (2013); 10.1063/1.4833239 Communication: Momentum-resolved quantum interference in optically excited surface states J. Chem. Phys. 135, 031101 (2011); 10.1063/1.3615541 Theory Of Interference Of Large Molecules AIP Conf. Proc. 899, 167 (2007); 10.1063/1.2733089 Interference with correlated photons: Five quantum mechanics experiments for undergraduates Am. J. Phys. 73, 127 (2005); 10.1119/1.1796811 Erratum: “Quantum interference experiments with large molecules” [Am. J. Phys. 71 (4), 319–325 (2003)] Am. J. Phys. 71, 1084 (2003); 10.1119/1.1603277 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 128.118.49.21 On: Tue, 23 Dec 2014 19:02:58 Quantum interference experiments with large molecules Olaf Nairz,a) Markus Arndt, and Anton Zeilingerb) Institut fu¨r Experimentalphysik, Universita¨t Wien, Boltzmanngasse 5, A-1090 Wien, Austria ͑Received 27 June 2002; accepted 30 October 2002͒ Wave–particle duality is frequently the first topic students encounter in elementary quantum physics. Although this phenomenon has been demonstrated with photons, electrons, neutrons, and atoms, the dual quantum character of the famous double-slit experiment can be best explained with the largest and most classical objects, which are currently the fullerene molecules. -

Rigid Body Dynamics: Student Misconceptions and Their Diagnosis1
Rigid Body Dynamics: Student Misconceptions and Their Diagnosis1 D. L. Evans2, Gary L. Gray3, Francesco Costanzo4, Phillip Cornwell5, Brian Self6 Introduction: As pointed out by a rich body of research literature, including the three video case studies, Lessons from Thin Air, Private Universe, and, particularly, Can We Believe Our Eyes?, students subjected to traditional instruction in math, science and engineering often do not adequately resolve the misconceptions that they either bring to a subject or develop while studying a subject. These misconceptions, sometimes referred to as alternative views or student views of basic concepts because they make sense to the student, block the establishment of connections between basic concepts, connections which are necessary for understanding the macroconceptions that build on the basics. That is, the misconceptions of basic phenomena hinder the learning of further material that relies on understanding these concepts. The literature on misconceptions includes the field of particle mechanics, but does not include rigid body mechanics. For example, it has been established7 "that … commonsense beliefs about motion and force are incompatible with Newtonian concepts in most respects…" It is also known that replacing these "commonsense beliefs" with concepts aligned with modern thinking on science is extremely difficult to accomplish8. But a proper approach to accomplishing this replacement must begin with understanding what the misconceptions are, progress to being able to diagnose them, and eventually, reach the point whereby instructional approaches are developed for addressing them. In high school, college and university physics, research has led to the development of an assessment instrument called the Force Concept Inventory9 (FCI) that is now available for measuring the success of instruction in breaking these student misconceptions. -

Students' Depictions of Quantum Mechanics
Students’ depictions of quantum mechanics: a contemporary review and some implications for research and teaching Johan Falk January 2007 Dissertation for the degree of Licentiate of Philosophy in Physics within the specialization Physics Education Research Uppsala University, 2007 Abstract This thesis presents a comprehensive review of research into students’ depic- tions of quantum mechanics. A taxonomy to describe and compare quantum mechanics education research is presented, and this taxonomy is used to highlight the foci of prior research. A brief history of quantum mechanics education research is also presented. Research implications of the review are discussed, and several areas for future research are proposed. In particular, this thesis highlights the need for investigations into what interpretations of quantum mechanics are employed in teaching, and that classical physics – in particular the classical particle model – appears to be a common theme in students’ inappropriate depictions of quantum mechanics. Two future research projects are presented in detail: one concerning inter- pretations of quantum mechanics, the other concerning students’ depictions of the quantum mechanical wave function. This thesis also discusses teaching implications of the review. This is done both through a discussion on how Paper 1 can be used as a resource for lecturers and through a number of teaching suggestions based on a merging of the contents of the review and personal teaching experience. List of papers and conference presentations Falk, J & Linder, C. (2005). Towards a concept inventory in quantum mechanics. Presentation at the Physics Education Research Conference, Salt Lake City, Utah, August 2005. Falk, J., Linder, C., & Lippmann Kung, R. (in review, 2007). -

Investigations of Nuclear Decay Half-Lives Relevant to Nuclear Astrophysics
DE TTK 1949 Investigations of nuclear decay half-lives relevant to nuclear astrophysics PhD Thesis Egyetemi doktori (PhD) ´ertekez´es J´anos Farkas Supervisor / T´emavezet˝o Dr. Zsolt F¨ul¨op University of Debrecen PhD School in Physics Debreceni Egyetem Term´eszettudom´anyi Doktori Tan´acs Fizikai Tudom´anyok Doktori Iskol´aja Debrecen 2011 Prepared at the University of Debrecen PhD School in Physics and the Institute of Nuclear Research of the Hungarian Academy of Sciences (ATOMKI) K´esz¨ult a Debreceni Egyetem Fizikai Tudom´anyok Doktori Iskol´aj´anak magfizikai programja keret´eben a Magyar Tudom´anyos Akad´emia Atommagkutat´o Int´ezet´eben (ATOMKI) Ezen ´ertekez´est a Debreceni Egyetem Term´eszettudom´anyi Doktori Tan´acs Fizikai Tudom´anyok Doktori Iskol´aja magfizika programja keret´eben k´esz´ıtettem a Debreceni Egyetem term´eszettudom´anyi doktori (PhD) fokozat´anak elnyer´ese c´elj´ab´ol. Debrecen, 2011. Farkas J´anos Tan´us´ıtom, hogy Farkas J´anos doktorjel¨olt a 2010/11-es tan´evben a fent megnevezett doktori iskola magfizika programj´anak keret´eben ir´any´ıt´asommal v´egezte munk´aj´at. Az ´ertekez´esben foglalt eredm´e- nyekhez a jel¨olt ¨on´all´oalkot´otev´ekenys´eg´evel meghat´aroz´oan hozz´a- j´arult. Az ´ertekez´es elfogad´as´at javaslom. Debrecen, 2011. Dr. F¨ul¨op Zsolt t´emavezet˝o Investigations of nuclear decay half-lives relevant to nuclear astrophysics Ertekez´es´ a doktori (PhD) fokozat megszerz´ese ´erdek´eben a fizika tudom´any´agban ´Irta: Farkas J´anos, okleveles fizikus ´es programtervez˝omatematikus K´esz¨ult a Debreceni Egyetem Fizikai Tudom´anyok Doktori Iskol´aja magfizika programja keret´eben T´emavezet˝o: Dr. -

PHYSICS 360 Quantum Mechanics
PHYSICS 360 Quantum Mechanics Prof. Norbert Neumeister Department of Physics and Astronomy Purdue University Spring 2020 http://www.physics.purdue.edu/phys360 Course Format • Lectures: – Time: Monday, Wednesday 9:00 – 10:15 – Lecture Room: PHYS 331 – Instructor: Prof. N. Neumeister – Office hours: Tuesday 2:00 – 3:00 PM (or by appointment) – Office: PHYS 372 – Phone: 49-45198 – Email: [email protected] (please use subject: PHYS 360) • Grader: – Name: Guangjie Li – Office: PHYS 6A – Phone: 571-315-3392 – Email: [email protected] – Office hours: Monday: 1:30 pm – 3:30 pm, Friday: 1:00 pm – 3:00 pm Purdue University, Physics 360 1 Textbook The textbook is: Introduction to Quantum Mechanics, David J. Griffiths and Darrell F. Schroeter, 3rd edition We will follow the textbook quite closely, and you are strongly encouraged to get a copy. Additional references: • R.P. Feynman, R.b. Leighton and M. Sands: The Feynman Lectures on Physics, Vol. III • B.H. brandsen and C.J. Joachain: Introduction To Quantum Mechanics • S. Gasiorowicz: Quantum Physics • R. Shankar: Principles Of Quantum Mechanics, 2nd edition • C. Cohen-Tannoudji, B. Diu and F. Laloë: Quantum Mechanics, Vol. 1 and 2 • P.A.M. Dirac: The Principles Of Quantum Mechanics • E. Merzbacher: Quantum Mechanics • A. Messiah: Quantum Mechanics, Vol. 1 and 2 • J.J. Sakurai: Modern Quantum Mechanics Purdue University, Physics 360 2 AA fewA (randomfew recommended but but but recommended) recommended) recommended) books books booksBooks B. H. Bransden and C. J. Joachain, Quantum Mechanics, (2nd B. H. H.B. H. Bransden Bransden Bransden and andand C. C. C. J. J. -

Teaching Light Polarization by Putting Art and Physics Together
Teaching Light Polarization by Putting Art and Physics Together Fabrizio Logiurato Basic Science Department, Ikiam Regional Amazonian University, Ecuador Physics Department, Trento University, Italy molecules. In mechanical engineering birefringence is exploited to detect stress in structures. Abstract—Light Polarization has many technological Unfortunately, light polarization is usually considered a applications and its discovery was crucial to reveal the transverse marginal concept in school programs. In order to fill this gap, nature of the electromagnetic waves. However, despite its we have developed an interdisciplinary laboratory on this fundamental and practical importance, in high school this property of subject for high school and undergraduate students. In this one light is often neglected. This is a pity not only for its conceptual relevance, but also because polarization gives the possibility to pupils have the possibility to understand the physics of light perform many beautiful experiments with low cost materials. polarization, its connections with the chemistry and the basics Moreover, the treatment of this matter lends very well to an of its applications. Beautiful and fascinating images appear interdisciplinary approach, between art, biology and technology, when we set between two crossed polarizing filters some which usually makes things more interesting to students. For these materials. The pictures that we can see are similar to those of reasons we have developed a laboratory on light polarization for high the abstract art. Students can create their own artistic school and undergraduate students. They can see beautiful pictures when birefringent materials are set between two crossed polarizing compositions, take photos of them and make their experiments filters. -

Integrated Dynamics and Statics for First Semester Sophomores in Mechanical Engineering
AC 2010-845: INTEGRATED DYNAMICS AND STATICS FOR FIRST SEMESTER SOPHOMORES IN MECHANICAL ENGINEERING Sherrill Biggers, Clemson University Sherrill B. Biggers is Professor of Mechanical Engineering at Clemson University. He has over 29 years of experience in teaching engineering mechanics, including statics, dynamics, and strength of materials at two universities. His technical research is in the computational mechanics and optimal design of advanced composite structures. He developed advanced structural mechanics design methods in the aerospace industry for over 10 years. Recently he has also contributed to research being conducted in engineering education. He received teaching awards at Clemson and the University of Kentucky. He has been active in curriculum and course development over the past 20 years. He received his BS in Civil Engineering from NC State University and his MS and Ph.D. in Civil Engineering from Duke University. Marisa Orr, Clemson University Marisa K. Orr is a doctoral candidate in the Mechanical Engineering program at Clemson University. She is a research assistant in the Department of Engineering and Science Education and is a member of the inaugural class of the Engineering and Science Education Certificate at Clemson University. As an Endowed Teaching Fellow, she received the Departmental Outstanding Teaching Assistant Award for teaching Integrated Statics and Dynamics for Mechanical Engineers. Her research involves analysis of the effects of student-centered active learning in sophomore engineering courses, and investigation of the career motivations of women and men as they relate to engineering. Lisa Benson, Clemson University Page 15.757.1 Page © American Society for Engineering Education, 2010 Integrated Dynamics and Statics for First Semester Sophomores in Mechanical Engineering Abstract A modified SCALE-UP approach that emphasizes active learning, guided inquiry, and student responsibility has been described as applied to an innovative and challenging sophomore course that integrates Dynamics and Statics. -
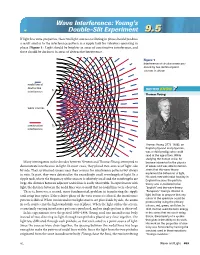
Wave Interference: Young's Double-Slit Experiment
Wave Interference: Young’s Double-Slit Experiment 9.59.5 If light has wave properties, then two light sources oscillating in phase should produce a result similar to the interference pattern in a ripple tank for vibrators operating in phase (Figure 1). Light should be brighter in areas of constructive interference, and there should be darkness in areas of destructive interference. Figure 1 Interference of circular waves pro- duced by two identical point sources in phase nodal line of destructive S DID YOU KNOW interference 1 ?? Thomas Young wave sources constructive S2 interference Thomas Young (1773–1829), an English physicist and physician, was a child prodigy who could read at the age of two. While studying the human voice, he Many investigators in the decades between Newton and Thomas Young attempted to became interested in the physics demonstrate interference in light. In most cases, they placed two sources of light side of waves and was able to demon- by side. They scrutinized screens near their sources for interference patterns but always strate that the wave theory in vain. In part, they were defeated by the exceedingly small wavelength of light. In a explained the behaviour of light. His work met with initial hostility in ripple tank, where the frequency of the sources is relatively small and the wavelengths are England because the particle large, the distance between adjacent nodal lines is easily observable. In experiments with theory was considered to be light, the distance between the nodal lines was so small that no nodal lines were observed. “English” and the wave theory There is, however, a second, more fundamental, problem in transferring the ripple “European.” Young’s interest in tank setup into optics. -

Diffraction Computing Systems 4 – Diffraction
Dept. of Electrical Engin. & 1 Lecture 4 – Diffraction Computing Systems 4 – Diffraction ! What is each photo? What is similar for each? EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 2 Today… Computing Systems ! Today, we will mainly use wave optics to understand diffraction… ! The Photonics book relies on Fourier optics to explain this, which is too advanced for this course. Credit: Fund. Photonics – Fig. 2.3-1 Credit: Fund. Photonics – Fig. 1.0-1 ! Topics: ! This lecture has several (1) Hygens-Fresnel principle nice animations that can be (2) Single and double slit diffraction viewed in the powerpoint (3) Diffraction (‘holographic’) cards version (slide show format). Figures today are mainly from CH1 of Fund. of Photonics or wiki. EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 3 Review Computing Systems ! You could freeze a photon ! You could also freeze in time (image below) and your position and observe observe sinusoidal with sinusoidal with respect to respect to distance (kx). time (wt). ! Lastly, we can just track E, and just show peak as plane waves: E = Emax sin(wt − kx) B = Bmax sin(wt − kx) w = angular freq. (2π f, radians / s) k = angular wave number (2π / λ, radians / m) EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 4 Review Computing Systems ! Split a laser beam (coherent / plane waves) and bringing the beams back together to produce interference fringes… we will do that today also, but with an added effect of diffraction… EECS 6048 – Optics for Engineers © Instructor – Prof. -

Genevieve Mathieson
THOMAS YOUNG, QUAKER SCIENTIST by GENEVIEVE MATHIESON Submitted in partial fulfillment of the requirements For the degree of Master of Arts Thesis Advisor: Dr. Gillian Weiss Department of History CASE WESTERN RESERVE UNIVERSITY January, 2008 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of ______________________________________________________ candidate for the ________________________________degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. ii Table of Contents Acknowledgements............................................................................................................iii Abstract.............................................................................................................................. iv I. Introduction ..................................................................................................................... 1 II. The Life and Work of Thomas Young........................................................................... 3 Childhood and Education as a Quaker...........................................................................