DOCSLIB.ORG

Young and Fresnel

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Young and Fresnel YOUNG AND FRESNEL: A CASE-STUDY INVESTIGATING THE PROGRESS OF THE WAVE THEORY IN THE BEGINNING OF THE NINETEENTH CENTURY IN THE LIGHT OF ITS IMPLICATIONS TO THE HISTORY AND METHODOLOGY OF SCIENCE A THESIS SUBMITTED TO THE GRADUATE SCHOOL OF SOCIAL SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY BY YEVGENIYA KULANDINA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF ARTS IN THE DEPARTMENT OF PHILOSOPHY SEPTEMBER 2013 Approval of the Graduate School of Social Sciences Prof. Dr. Meliha Altunışık Director I certify that this thesis satisfies all the requirements as a thesis for the degree of Master of Arts. Prof. Dr. Ahmet İnam Head of Department This is to certify that we have read this thesis and that in our opinion it is fully adequate, in scope and quality, as a thesis for the degree of Master of Arts. Doç. Dr. Samet Bağçe Supervisor Examining Committee Members Prof. Dr. Ahmet İnam (METU, PHIL) Doç. Dr. Samet Bağçe (METU, PHIL) Doç. Dr. Burak Yedierler (METU, PHYS) I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work. Name, Last name : Yevgeniya Kulandina Signature : iii ABSTRACT YOUNG AND FRESNEL: A CASE-STUDY INVESTIGATING THE PROGRESS OF THE WAVE THEORY IN THE BEGINNING OF THE NINETEENTH CENTURY IN THE LIGHT OF ITS IMPLICATIONS TO THE HISTORY AND METHODOLOGY OF SCIENCE Kulandina, Yevgeniya MA, Department of Philosophy Supervisor: Doç. Dr. Samet Bağçe September 2013, 78 pages This thesis aims to analyze how Thomas Young and Augustine Fresnel were successful in developing the wave theory of light at the beginning of the nineteenth century. The Methodology of Scientific Research Programmes will be used as the tool of analysis. Such a case-study will give the possibility to access the relative merits of the chosen methodology as well – it will help to point to the benefits of the method and to the parts which are open to further modification. That in turn will allow to discuss general issues appearing in the history and methodology of science, such as the applicability of a certain set of methodological rules to the process of theory-change throughout the flow of scientific development, the status of these rules as a guarantee of objectivity of scientific theories, and the possibility of scientific inquiry as objective process. Keywords: Wave Theory of Light, Young, Fresnel, Methodology of Science. iv ÖZ YOUNG VE FRESNEL: BİLİM TARİHİ VE METODOLOJİSİNE ETKİLER IŞIĞINDA ON DOKUZUNCU YÜZYILIN BAŞINDA DALGA TEORİSİNDEKİ GELİŞMEYİ İNCELEYEN DURUM ÇALIŞMASI Kulandina, Yevgeniya Yüksek Lisans, Felsefe Bölümü Tez Yöneticisi: Doç. Dr. Samet Bağçe Eylül 2013, 78 sayfa Bu tez, Thomas Young ve Augistive Fresnel’in, on dokuzuncu yüzyılın başındaki dalga ışık teorisinin gelişiminde ne kadar başarılı olduklarını incelemektedir. İnceleme aracı olarak, Bilimsel Araştırma Programların Metodolojisi kullanılacaktır. Bu durum çalışması, seçilmiş olan metodolojinin göreceli değerlerinin erişimine de olanak verecektir – çalışma, metodun faydalarına ve düzeltmeye açık noktalarına işaret etmesinde yardımcı olacaktır. Bu da, bir takım metodolojik kuralların teoriler değişimi sürecine bilimsel gelişimin boyunca uygulanabirliği, bu kuralların bilimsel teorilerin objektiflik garantisi olarak statüsü ve bilimsel araştırmanın objektif bir süreç olarak sürdürme olasılığı gibi bilim tarihi ve metodolojisinde çıkan genel meselelerini tartışmak için olanak sağlayacaktır. Anahtar Kelimeler: Dalga Işık Teorisi, Young, Fresnel, Bilim Metodolojisi. v To My Dear Mother vi TABLE OF CONTENTS PLAGIARISM........................................................................................................iii ABSTRACT ....................................................................................................... iv ÖZ ....................................................................................................................... v DEDICATION.................................................................................................... vi TABLE OF CONTENTS ................................................................................... vii LIST OF TABLES ............................................................................................ viii LIST OF FIGURES ........................................................................................... ix CHAPTER I. INTRODUCTION ................................................................................ 1 II. HISTORICAL BACKGROUND: THE HERITAGE ACCOMODATED IN THE WAVE THEORY TILL 1800 .................. 4 III. THOMAS YOUNG AND THE PRINCIPLE OF INTERFERENCE .................................................... 11 IV. AUGUSTINE FRESNEL AND THE CELEBRATED ACADEMY PRIZE ......................................... 21 V. WHY THE METHODOLOGY OF SCIENTIFIC RESEARCH PROGRAMMES? .................................. 43 VI. FURTHER EVALUATIONS ON THE YOUNG-FRESNEL CASE ........................................................ 49 VII. CONCLUSION: WHO MADE THE REVOLUTION IN OPTICS IN THE NINETEENTH CENTURY? ............................ 66 REFERENCES .................................................................................................. 76 APPENDICES A. TEZ FOTOKOPİSİ İZİN FORMU ...................................................... 78 vii LIST OF TABLES TABLES Table 2.1. Young’s observations on diffraction .................................................. 19 Table 3.1. Comparing theory and experiment, the fourth dark band .................... 25 Table 3.2. Table of the numerical values of the integrals .................................... 39 Table 3.3. Comparing theoretical and experimental results on the exterior fringes of red-light of wave-length 0.000638 mm ............................................... 41 Table 3.4. Comparing theory with experiment regarding of positions of maxima and minima in the fringes produced by a narrow aperture ..................... 41 viii LIST OF FIGURES FIGURES Figure 2.1. Constructive and destructive interference ......................................... 16 Figure 3.1. External and internal fringes formed by diffraction from an obstacle ............................................................................... 22 Figure 3.2. Observation of the dark fringe of the fourth order ............................. 25 Figure 3.3. Fresnel’s experiment with mirror and copper cylinders..................... 27 Figure 3.4. Fresnel’s initial explanation of diffraction ........................................ 29 Figure 3.5. Copper plate used in Fresnel’s experiment ....................................... 32 Figure 3.6. The scheme of interference of two waves ......................................... 33 Figure 3.7. Incorporation of the Huygens’s principle to the phenomenon of diffraction of light ............................................................... 36 Figure 3.8. Observation of diffraction from an obstacle ...................................... 37 ix CHAPTER I INTRODUCTION Through the course of its development, scientific activity gives birth to a certain amount of examples, which in turn become quite interesting to investigate from the standpoint of the methodology of science. One of the most suitable candidate for such a methodological analysis would be the process of theory-change. It is found to be convenient since the examination of the shift from one scientific theory to another allows to track and understand the processes taking place during the change by the help of the chosen methodological “tools” of analysis. Moreover, such examination gives a chance to evaluate chosen methodological set of rules as well, test them “in action”, so-to-speak. The shift of “paradigms” from Ptolemy’s geocentric system to Copernicus’s heliocentric picture of the universe, or shift from Newtonian mechanics to the General Theory of Relativity – these can be noticed as the most prominent examples used for such purpose. Still, there are other cases in the history of science which deserve close attention. One of these can be found in optics at the beginning of the nineteenth century, when the particle theory of light, developed by Isaac Newton, was abandoned in the favor of the wave theory of light. This case is fruitful from the methodological point of view not only as a bright example of the process of theory-change; a closer look at it uncovers an interesting fact in that switch. When one reads a book in the history of the wave theory of light (also to be referred as “the wave theory” further), two scientists can be separated as major dedicators to this hypothesis – Thomas Young (1773 – 1829) and Augustine Fresnel (1788 – 1827). The former worked in England; the latter developed his hypothesis in France. There appears to be no concern at the first glance; but a closer examination would show that Young established his theory of light in the early 1800s, but the acceptance of the wave theory among scientists began only twenty years later, after Fresnel announced his hypothesis. If Young had 1 successfully demonstrated his theory as valid, why then it was neglected for almost twenty years? Which factors played role in such a delay? What was there in Fresnel’s formulation about the wave nature of light that allowed to convince the men of science in its validity; and how in that respect Young’s work left incomplete?
Load more

Recommended publications
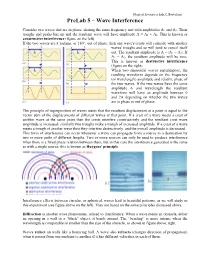
  • Prelab 5 – Wave Interference
    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
    [Show full text]
  • On an Experimentum Crucis for Optics
    Research Report: On an Experimentum Crucis for Optics Ionel DINU, M.Sc. Teacher of Physics E-mail: [email protected] (Dated: November 17, 2010) Abstract Formulated almost 150 years ago, Thomas Young’s hypothesis that light might be a transverse wave has never been seriously questioned, much less subjected to experiment. In this article I report on an attempt to prove experimentally that Young’s hypothesis is untenable. Although it has certain limitations, the experiment seems to show that sound in air, a longitudinal wave, can be “polarized” by reflection just like light, and this can be used as evidence against Young’s hypothesis. Further refinements of the experimental setup may yield clearer results, making this report useful to those interested in the important issue of whether light is a transverse or a longitudinal wave. Introduction In the course of development of science, there has always been a close connection between sound and light [1]. Acoustics stimulated research and discovery in optics and vice-versa. Reflection and refraction being the first common points observed between the two, the analogy between optical and acoustical phenomena has been proven also in the case of interference, diffraction, Doppler effect, and even in their mode of production: sounds are produced by the vibration of macroscopic objects, while light is produced by vibrating molecules and atoms. The wave nature of sound implies that light is also a wave and, if matter must be present for sound to be propagated, then aether must exist in order to account for the propagation of light through spaces void of all the matter known to chemistry.
    [Show full text]
  • Quantum Interference Experiments with Large Molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger
    Quantum interference experiments with large molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger Citation: American Journal of Physics 71, 319 (2003); doi: 10.1119/1.1531580 View online: http://dx.doi.org/10.1119/1.1531580 View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/71/4?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Quantum interference and control of the optical response in quantum dot molecules Appl. Phys. Lett. 103, 222101 (2013); 10.1063/1.4833239 Communication: Momentum-resolved quantum interference in optically excited surface states J. Chem. Phys. 135, 031101 (2011); 10.1063/1.3615541 Theory Of Interference Of Large Molecules AIP Conf. Proc. 899, 167 (2007); 10.1063/1.2733089 Interference with correlated photons: Five quantum mechanics experiments for undergraduates Am. J. Phys. 73, 127 (2005); 10.1119/1.1796811 Erratum: “Quantum interference experiments with large molecules” [Am. J. Phys. 71 (4), 319–325 (2003)] Am. J. Phys. 71, 1084 (2003); 10.1119/1.1603277 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 128.118.49.21 On: Tue, 23 Dec 2014 19:02:58 Quantum interference experiments with large molecules Olaf Nairz,a) Markus Arndt, and Anton Zeilingerb) Institut fu¨r Experimentalphysik, Universita¨t Wien, Boltzmanngasse 5, A-1090 Wien, Austria ͑Received 27 June 2002; accepted 30 October 2002͒ Wave–particle duality is frequently the first topic students encounter in elementary quantum physics. Although this phenomenon has been demonstrated with photons, electrons, neutrons, and atoms, the dual quantum character of the famous double-slit experiment can be best explained with the largest and most classical objects, which are currently the fullerene molecules.
    [Show full text]
  • Thomas Young the Man Who Knew Everything
    Thomas Young The man Who Knew Everything Andrew Robinson marvels at the brain power and breadth of knowledge of the 18th-century polymath Thomas Young. He examines his relationship with his contemporaries, particularly with the French Egyptologist Champollion, and how he has been viewed subsequently by historians. ORTUNATE NEWTON, happy professor of natural philosophy at childhood of science!’ Albert the newly founded Royal Institution, F Einstein wrote in 1931 in his where in 1802-03 he delivered what foreword to the fourth edition of is generally regarded as the most far- Newton’s influential treatise Opticks, reaching series of lectures ever given originally published in 1704. by a scientist; a physician at a major London hospital, St George’s, for a Nature to him was an open book, quarter of a century; the secretary of whose letters he could read without the Admiralty’s Board of Longitude effort. ... Reflection, refraction, the and superintendent of its vital Nauti- formation of images by lenses, the cal Almanac from 1818 until his mode of operation of the eye, the death; and ‘inspector of calculations’ spectral decomposition and recom- for a leading life insurance company position of the different kinds of in the 1820s. In 1794, he was elected light, the invention of the reflecting a fellow of the Royal Society at the telescope, the first foundations of age of barely twenty-one, became its colour theory, the elementary theory foreign secretary at the age of thirty, of the rainbow pass by us in and turned down its presidency in procession, and finally come his his fifties.
    [Show full text]
  • Quantum Weirdness: a Beginner's Guide
    Quantum Weirdness: A Beginner’s Guide Dr. Andrew Robinson Part 1 Introduction The Quantum Jump 9:38 AM About Me • From Bakewell • PhD in Physical Chemistry • Worked in Berlin, Liverpool, Birmingham • In Canada since 2000 • Worked at University of Saskatchewan • Moved to Ottawa in 2010 • Teach Physics at Carleton 9:38 AM In This Lecture Series • We will talk about • What does Quantum Mean? • Quantum Effects • What are the ramifications of Quantum Theory • How Quantum Theory impacts our everyday lives • I will show a few equations, but you don’t need to know any mathematics • Please ask questions at any time 9:38 AM Books “How to Teach Quantum Physics to your Dog” by Chad Orzel “30-Second Quantum Theory” By Brian Clegg (ed.) 9:38 AM Definition of “Quantum” Physics • A discrete quantity of energy proportional in magnitude to the frequency of the radiation it represents. Legal • A required or allowed amount, especially an amount of money legally payable in damages. 9:38 AM • Quantum Satis “as much as is sufficient“ – pharmacology and medicine • Quantum Salis “the amount which is enough” • Quantum comes from the Latin word quantus, meaning "how great". Used by the German Physicist Hermann von Helmholtz ( who was also a physician) in the context of the electron (quanta of electricity) Use by Einstein in 1905 "Lichtquanta” – particle of light 9:38 AM “Quantum Jump” & “Quantum Leap” • Colloquially “A sudden large increase or advance”. • In physics “A jump between two discrete energy levels in a quantum system” (Actually a rather small leap in terms of energy!) 9:38 AM Quantum Properties in Physics • Properties which can only take certain values When you are on the ladder, you must be on one of the steps: 4 1 3 2 Quantum 2 3 Numbers 1 4 9:38 AM • Not every quantity in physics is quantized • Your height from the ground when on the slide varies continuously Maximum height Minimum9:38 AM height • Whether you can treat the system as continuous, or quantum depends on the scale.
    [Show full text]
  • Thomas Young's Research on Fluid Transients: 200 Years On
    Thomas Young's research on fluid transients: 200 years on Arris S Tijsseling Alexander Anderson Department of Mathematics School of Mechanical and Computer Science and Systems Engineering Eindhoven University of Technology Newcastle University P.O. Box 513, 5600 MB Eindhoven Newcastle upon Tyne NE1 7RU The Netherlands United Kingdom ABSTRACT Thomas Young published in 1808 his famous paper (1) in which he derived the pressure wave speed in an incompressible liquid contained in an elastic tube. Unfortunately, Young's analysis was obscure and the wave speed was not explicitly formulated, so his achievement passed unnoticed until it was rediscovered nearly half a century later by the German brothers Weber. This paper briefly reviews Young's life and work, and concentrates on his achievements in the area of hydraulics and waterhammer. Young's 1808 paper is “translated” into modern terminology. Young's discoveries, though difficult for modern readers to identify, appear to include most if not all of the key elements which would subsequently be combined into the pressure rise equation of Joukowsky. Keywords waterhammer, fluid transients, solid transients, wave speed, history, Thomas Young NOTATION c sonic wave speed, m/s p fluid pressure, Pa D internal tube diameter, m R internal tube radius, m E Young’s modulus, Pa t time, s e tube wall thickness, m v velocity, m/s f elastic limit, Pa x length, m g gravitational acceleration, m/s 2 δ change, jump h height, pressure head, m ε longitudinal strain K fluid bulk modulus, Pa ρ mass density, kg/m
    [Show full text]
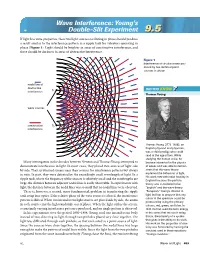
  • Wave Interference: Young's Double-Slit Experiment
    Wave Interference: Young’s Double-Slit Experiment 9.59.5 If light has wave properties, then two light sources oscillating in phase should produce a result similar to the interference pattern in a ripple tank for vibrators operating in phase (Figure 1). Light should be brighter in areas of constructive interference, and there should be darkness in areas of destructive interference. Figure 1 Interference of circular waves pro- duced by two identical point sources in phase nodal line of destructive S DID YOU KNOW interference 1 ?? Thomas Young wave sources constructive S2 interference Thomas Young (1773–1829), an English physicist and physician, was a child prodigy who could read at the age of two. While studying the human voice, he Many investigators in the decades between Newton and Thomas Young attempted to became interested in the physics demonstrate interference in light. In most cases, they placed two sources of light side of waves and was able to demon- by side. They scrutinized screens near their sources for interference patterns but always strate that the wave theory in vain. In part, they were defeated by the exceedingly small wavelength of light. In a explained the behaviour of light. His work met with initial hostility in ripple tank, where the frequency of the sources is relatively small and the wavelengths are England because the particle large, the distance between adjacent nodal lines is easily observable. In experiments with theory was considered to be light, the distance between the nodal lines was so small that no nodal lines were observed. “English” and the wave theory There is, however, a second, more fundamental, problem in transferring the ripple “European.” Young’s interest in tank setup into optics.
    [Show full text]
  • Three Music-Theory Lessons
    Three Music-Theory Lessons The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Rehding, Alexander. 2016. “Three Music-Theory Lessons.” Journal of the Royal Musical Association 141 (2) (July 2): 251–282. doi:10.1080/02690403.2016.1216025. Published Version doi:10.1080/02690403.2016.1216025 Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:34220771 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP Three Music Theory Lessons ALEXANDER REHDING To make the familiar strange and the strange familiar was as much a central feature of Novalis’ conception of Romanticism as it is a mainstay of semiotics.1 In this spirit, we will begin with what seems like a mundane description of music- theoretical practice. If we enter a music theory classroom in the western world, we would normally expect to find a number of objects. We see a blackboard, ideally with five-line staffs already printed on it. We also expect a piano in the room, and we would probably have some sheet music, perhaps with the quintessential music theory teaching material: Bach chorale harmonizations. Let’s further imagine it is this passage, the simple opening line of the Lutheran hymn “Wie schön leuchtet der Morgenstern,” from Bach’s Cantata BWV 1, shown in Fig. 1, that is marked on the board.
    [Show full text]
  • Diffraction Computing Systems 4 – Diffraction
    Dept. of Electrical Engin. & 1 Lecture 4 – Diffraction Computing Systems 4 – Diffraction ! What is each photo? What is similar for each? EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 2 Today… Computing Systems ! Today, we will mainly use wave optics to understand diffraction… ! The Photonics book relies on Fourier optics to explain this, which is too advanced for this course. Credit: Fund. Photonics – Fig. 2.3-1 Credit: Fund. Photonics – Fig. 1.0-1 ! Topics: ! This lecture has several (1) Hygens-Fresnel principle nice animations that can be (2) Single and double slit diffraction viewed in the powerpoint (3) Diffraction (‘holographic’) cards version (slide show format). Figures today are mainly from CH1 of Fund. of Photonics or wiki. EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 3 Review Computing Systems ! You could freeze a photon ! You could also freeze in time (image below) and your position and observe observe sinusoidal with sinusoidal with respect to respect to distance (kx). time (wt). ! Lastly, we can just track E, and just show peak as plane waves: E = Emax sin(wt − kx) B = Bmax sin(wt − kx) w = angular freq. (2π f, radians / s) k = angular wave number (2π / λ, radians / m) EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 4 Review Computing Systems ! Split a laser beam (coherent / plane waves) and bringing the beams back together to produce interference fringes… we will do that today also, but with an added effect of diffraction… EECS 6048 – Optics for Engineers © Instructor – Prof.
    [Show full text]
  • Blackbody” Radiation
    Applications of Photonics Technologies 2019 Introduction: what is light and basic properties Cristina Masoller [email protected] www.fisica.edu.uy/~cris MÀSTER UNIVERSITARI EN ENGINYERIA DE SISTEMES AUTOMÀTICS I ELECTRÒNICA INDUSTRIAL MÀSTER UNIVERSITARI EN ENGINYERIA AERONÀUTICA MÀSTER UNIVERSITARI EN ENGINYERIA INDUSTRIAL Introducing myself • Originally from Montevideo, Uruguay • PhD in physics (lasers, Bryn Mawr College, USA 1999) • Since 2004 @ Universitat Politecnica de Catalunya • Profesora Catedratica, Physics Department, research group on Dynamics, Nonlinear Optics and Lasers • Web page: http://www.fisica.edu.uy/~cris/ Introducing our research group Dynamics, Nonlinear Optics and Lasers Senior researchers / PhD students: 11/8 Introducing our research group . Research topics: Nonlinear phenomena (photonics, biophysics, complex systems) . Lab facilities in Gaia Building, UPC Terrassa: . Website: https://donll.upc.edu 4 Learning objectives and references . To understand the basic properties of light, which will allow us to understand photonic techniques and applications. There is no required text. The slides are based on previous courses by Prof. Ramon Vilaseca (UPC Prof. Emerito), the slides of Prof. Rick Trebino (Georgia Tech, USA) and freely available material in the Optical Society (OSA) web page. 5 what is light? Particles and waves Particles are localized in space and time (classical physics). Particles have well-defined trajectories. Waves are extended in space and time. Waves have poorly defined trajectories. waves bend around corners (diffraction) Two ways in which energy is transported Point-mass interaction, which transfers energy and momentum: particles. Extended regions wherein energy is transferred by vibrations and rotations (collective motions of particles): waves. Poll Is light constituted by particles or by waves? 9 The nature of light: Huygens Huygens promoted the wave theory.
    [Show full text]
  • Thomas Young and Eighteenth-Century Tempi Peter Pesic St
    Performance Practice Review Volume 18 | Number 1 Article 2 Thomas Young and Eighteenth-Century Tempi Peter Pesic St. John's College, Santa Fe, New Mexico Follow this and additional works at: http://scholarship.claremont.edu/ppr Pesic, Peter (2013) "Thomas Young and Eighteenth-Century Tempi," Performance Practice Review: Vol. 18: No. 1, Article 2. DOI: 10.5642/perfpr.201318.01.02 Available at: http://scholarship.claremont.edu/ppr/vol18/iss1/2 This Article is brought to you for free and open access by the Journals at Claremont at Scholarship @ Claremont. It has been accepted for inclusion in Performance Practice Review by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. Thomas Young and Eighteenth-Century Tempi Dedicated to the memory of Ralph Berkowitz (1910–2011), a great pianist, teacher, and master of tempo. The uthora would like to thank the John Simon Guggenheim Memorial Foundation for its support as well as Alexei Pesic for kindly photographing a rare copy of Crotch’s Specimens of Various Styles of Music. This article is available in Performance Practice Review: http://scholarship.claremont.edu/ppr/vol18/iss1/2 Thomas Young and Eighteenth-Century Tempi Peter Pesic In trying to determine musical tempi, we often lack exact and authoritative sources, especially from the eighteenth century, before composers began to indicate metronome markings. Accordingly, any independent accounts are of great value, such as were collected in Ralph Kirkpatrick’s pioneering article (1938) and most recently sur- veyed in this journal by Beverly Jerold (2012).1 This paper brings forward a new source in the writings of the English polymath Thomas Young (1773–1829), which has been overlooked by musicologists because its author’s best-known work was in other fields.
    [Show full text]
  • Genevieve Mathieson
    THOMAS YOUNG, QUAKER SCIENTIST by GENEVIEVE MATHIESON Submitted in partial fulfillment of the requirements For the degree of Master of Arts Thesis Advisor: Dr. Gillian Weiss Department of History CASE WESTERN RESERVE UNIVERSITY January, 2008 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of ______________________________________________________ candidate for the ________________________________degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. ii Table of Contents Acknowledgements............................................................................................................iii Abstract.............................................................................................................................. iv I. Introduction ..................................................................................................................... 1 II. The Life and Work of Thomas Young........................................................................... 3 Childhood and Education as a Quaker...........................................................................
    [Show full text]