DOCSLIB.ORG

Genevieve Mathieson

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Genevieve Mathieson THOMAS YOUNG, QUAKER SCIENTIST by GENEVIEVE MATHIESON Submitted in partial fulfillment of the requirements For the degree of Master of Arts Thesis Advisor: Dr. Gillian Weiss Department of History CASE WESTERN RESERVE UNIVERSITY January, 2008 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of ______________________________________________________ candidate for the ________________________________degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. ii Table of Contents Acknowledgements............................................................................................................iii Abstract.............................................................................................................................. iv I. Introduction ..................................................................................................................... 1 II. The Life and Work of Thomas Young........................................................................... 3 Childhood and Education as a Quaker............................................................................ 3 Medical School and Young’s First Publication .............................................................. 7 Quakers and University................................................................................................... 9 Pursuing a Medical Career............................................................................................ 11 Disownment .................................................................................................................. 13 Early Optical Experiments............................................................................................ 16 The Royal Institution & Maturation of Young’s Optical Theories............................... 21 Leaving the Royal Institution........................................................................................ 27 Conflict with The Edinburgh Review............................................................................ 28 Medical Practice and Egyptology ................................................................................. 31 Revisiting Optics........................................................................................................... 34 Young as Bureaucrat..................................................................................................... 37 Young’s Later Life........................................................................................................ 41 III. Conclusions................................................................................................................. 43 Impediments to Young’s Optical Theories................................................................... 43 The Mathematical and Scientific Styles of the English and the French ....................... 48 Quaker Science and Quaker Schooling......................................................................... 50 Quakers in the Royal Society........................................................................................ 53 Young As Quaker Scientist........................................................................................... 56 Bibliography ..................................................................................................................... 60 iii Acknowledgements Firstly, I would like to thank the members of my committee for working with me during this endeavor. I am particularly grateful to Gillian Weiss and Alan Rocke for their involvement from the beginning. Without their support, suggestions, and assistance, this thesis would not exist. I remain grateful to all of my friends and family for their ongoing encouragement of and interest in my academic progress as well as for providing reminders that there is life outside of school. I don’t have enough space to thank each of them individually, but I must offer particular thanks to my parents for their confidence in me, to Angie and Brent Robinson for being enthusiastic early readers and to Mindy Miller for research assistance and cheerleading above and beyond the call of duty. Finally, I would like to thank my husband Jim for providing countless meals and constant moral support, for being a willing reader of drafts and for his unfaltering belief in my ability to see this project through. iv Thomas Young, Quaker Scientist Abstract by GENEVIEVE MATHIESON Thomas Young was a widely accomplished polymath who discovered the principle of interference of light. This was just one of his achievements, made in the midst of practicing medicine, working as both a professional scientist and bureaucrat, deciphering portions of the Rosetta stone, determining the causes of color vision, and writing prolifically on all of these topics. The interference of light was later shown by Fresnel to be conclusive proof that light was vibratory rather than corpuscular. Given Young’s strong support for vibratory theory, this thesis seeks to determine why Young did not pursue his optical theories further. Through study of Young’s Quaker upbringing, an analysis of Quaker schooling and scientific practice, Young’s work and its reception by his scientific peers, I argue that Young’s scientific practice was inextricably linked with his Quaker background. 1 I. Introduction Thomas Young was a polymath, a talented physician – though lacking in bedside manner – a natural philosopher, a linguist, and a bureaucrat. Throughout his life he varied roles so frequently, he could almost be charged with dilettantism. Nevertheless, Young’s accomplishments ranged widely. In physical optics, he discovered the principle of interference of light, explaining diffraction phenomena and supporting the vibratory or wave theory. In physiological optics, he was the first to suggest the existence of single- color receptors in the eye and is credited with discovering the causes of color vision and color blindness.1 He defined the modulus of elasticity (now labeled Young’s Modulus) as the ability of a material to withstand length changes due to compression or extension. He published a comprehensive treatise on consumptive diseases that was inspired by his own experience with tuberculosis, and a survey course of medical lectures. Young attempted to decipher the Rosetta Stone and was able to complete a version of the demotic text before Champollion completed his own decipherment of the hieroglyphics. Young’s industry was astounding; in addition to his scientific and linguistic research and publications, he also maintained a career as a physician and bureaucrat. Young was an ambitious man, but one who retained a strict adherence to honesty, extended to the point of tactlessness. He refused to soften a harsh truth and tended to assume that his audience was his intellectual equal, traits that explain both his failure as a Royal Institution lecturer and his only modest success as a physician. Young was born a Quaker, a Christian sect that rejected worldly goods and maintained a strict sense of morality. His parents were of modest means, but his great-uncle Richard Brocklesby’s 1 Thomas Young, “The Bakerian Lecture: On the Theory of Light and Colors.” Philosophical Transactions 92 (1802): 21. The theory is now called the Young-Helmholtz trichromatic theory, and refers to the cones in the eye. 2 social status and his grandfather’s insistence on a classical education gave Young the schooling and connections necessary to travel in rarified circles. His membership in the Royal Society connected him politically, his profession as physician provided him considerable income, and both combined with his intelligence to yield countless opportunities for research and publication. Despite Young’s widespread achievements, however, he did not always take his projects to completion. Although Young discovered the principle of interference of light and addressed a few interesting cases of diffraction, he demonstrated it only for two rays or sources of light and failed to apply it more widely to optics. As a proponent of the vibration or wave theory of light, Young also tried to use the principle of interference as proof of light’s vibratory nature. While Young lived to see his vibratory theory of light vindicated, he did not shift the paradigm himself. Given his brilliance and scientific ability, it is curious that Young himself was not able to take his discovery past simple demonstration and to its broadest application. In this paper I contend that Thomas Young’s early religious background was influential in forming his personality and character, and subsequently his scientific style. This paper, therefore, is an investigation of that relationship. By portraying Young’s life and work in a holistic fashion, I intend to demonstrate that Young’s scientific practice was inextricably linked to his Quaker upbringing. 3 II. The Life and Work of Thomas Young Childhood and Education as a Quaker Thomas Young was born in 1773 in Milverton, Somerset, to Sarah and Thomas Young. He was the eldest of ten children but spent little time in the company
Load more

Recommended publications
  • Differential Calculus and by Era Integral Calculus, Which Are Related by in Early Cultures in Classical Antiquity the Fundamental Theorem of Calculus
    History of calculus - Wikipedia, the free encyclopedia 1/1/10 5:02 PM History of calculus From Wikipedia, the free encyclopedia History of science This is a sub-article to Calculus and History of mathematics. History of Calculus is part of the history of mathematics focused on limits, functions, derivatives, integrals, and infinite series. The subject, known Background historically as infinitesimal calculus, Theories/sociology constitutes a major part of modern Historiography mathematics education. It has two major Pseudoscience branches, differential calculus and By era integral calculus, which are related by In early cultures in Classical Antiquity the fundamental theorem of calculus. In the Middle Ages Calculus is the study of change, in the In the Renaissance same way that geometry is the study of Scientific Revolution shape and algebra is the study of By topic operations and their application to Natural sciences solving equations. A course in calculus Astronomy is a gateway to other, more advanced Biology courses in mathematics devoted to the Botany study of functions and limits, broadly Chemistry Ecology called mathematical analysis. Calculus Geography has widespread applications in science, Geology economics, and engineering and can Paleontology solve many problems for which algebra Physics alone is insufficient. Mathematics Algebra Calculus Combinatorics Contents Geometry Logic Statistics 1 Development of calculus Trigonometry 1.1 Integral calculus Social sciences 1.2 Differential calculus Anthropology 1.3 Mathematical analysis
    [Show full text]
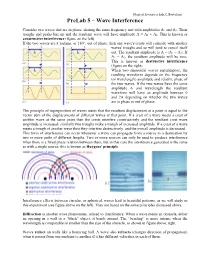
  • Prelab 5 – Wave Interference
    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
    [Show full text]
  • Stephan Hruszkewycz Tuesday, September 25 • 4 Pm • Tech L211
    THE MATERIALS SCIENCE AND ENGINEERING DEPARTMENT COLLOQUIUM SERIES PRESENTS: Stephan Hruszkewycz Assistant Physicist, Argonne National Laboratory Opportunities for materials science with coherent x-ray diffraction imaging Recent progress in 3D coherent x-ray diffraction imaging methods can enable high resolution structural imaging of nano-structured crystalline materials under operating conditions. In this talk, I discuss developments in Bragg coherent diffraction imaging (BCDI) that aim to broaden the envelope of materials science problems that can be addressed with the technique. Following an introduction of the basic principles of the method, two specific topics will be discussed: 1) BCDI at high x-ray energies that provide dramatic penetrating ability, 2) Bragg ptychography that enable imaging of targeted sub- volumes of a crystal. Both approaches will be discussed in the context of materials science problems that can be addressed in-situ at next-generation synchrotron storage rings including the Upgraded Advanced Photon Source project now underway at Argonne National Laboratory. Stephan Hruszkewycz is a staff scientist in the Materials Science Division at Argonne National Laboratory. His research focuses on developing and using coherent x-ray scattering techniques to interrogate nanoscale materials structure and dynamics under working conditions to reveal structure-property relationships. Currently he is using strain- sensitive coherent Bragg diffraction to image subtle strain fields in nanoscale crystals for photonic and quantum information applications. These research thrusts are pursued at high-brightness synchrotron sources with state-of-the-art coherence-preserving beamlines, including those at the Advanced Photon Source, NSLS-II, and LCLS, and aim to broaden the applicability of coherent diffraction imaging within both the broader materials science community.
    [Show full text]
  • Significance of Beating Observed in Earthquake Responses of Buildings
    SIGNIFICANCE OF BEATING OBSERVED IN EARTHQUAKE RESPONSES OF BUILDINGS Mehmet Çelebi1, S. Farid Ghahari2, and Ertuğrul Taciroǧlu2 U.S. Geological Survey1 and University of California, Los Angeles2 Menlo Park, California, USA1 and Los Angeles, California, USA2 Abstract The beating phenomenon observed in the recorded responses of a tall building in Japan and another in the U.S. are examined in this paper. Beating is a periodic vibrational behavior caused by distinctive coupling between translational and torsional modes that typically have close frequencies. Beating is prominent in the prolonged resonant responses of lightly damped structures. Resonances caused by site effects also contribute to accentuating the beating effect. Spectral analyses and system identification techniques are used herein to quantify the periods and amplitudes of the beating effects from the strong motion recordings of the two buildings. Quantification of beating effects is a first step towards determining remedial actions to improve resilient building performance to strong earthquake induced shaking. Introduction In a cursory survey of several textbooks on structural dynamics, it can be seen that beating effects have not been included in their scopes. On the other hand, as more earthquake response records from instrumented buildings became available, it also became evident that the beating phenomenon is common. As modern digital equipment routinely provide recordings of prolonged responses of structures, we were prompted to visit the subject of beating, since such response characteristics may impact the instantaneous and long-term shaking performances of buildings during large or small earthquakes. The main purpose in deploying seismic instruments in buildings (and other structures) is to record their responses during seismic events to facilitate studies understanding and assessing their behavior and performances during and future strong shaking events.
    [Show full text]
  • MEMOIRS Row Standing on the Stern, Venetian Style, from the Lido, Where I Lived, to the School in Venice, Where I Studied
    BRUNO BENEDETTO ROSSI April 13, 1905–November 21, 1993 BY GEORGE W. CLARK The initial motivation of the experiment which led to this discovery [of Sco X-1] was a subconscious feeling for the inexhaustible wealth of nature, a wealth that goes far beyond the imagination of man. That feeling was possi- bly generated by experiences in my previous work on cosmic rays; more likely it was inborn and was the reason why, as a young man, I went into the field of cosmic rays. In any case, whenever technical progress opened a new window into the surrounding world, I felt the urge to look through this window, hoping to see something unexpected.1 BEGINNINGS RUNO ROSSI WAS BORN April 13, 1905, in Venice, the el- Bdest of three sons of Rino Rossi and Lina Minerbi. His father was an electrical engineer whose successful career began with work on the electrification of Venice. He wrote in his autobiography2 that his father loved science and would have chosen it for a career except for practical consider- ations. He attributes to his father the influence that turned what may have been an “inborn tendency toward science . into a lifelong commitment.” He recalled: perfectly clear winter mornings when the air was so unusually transparent that the Alps surrounding Venice became clearly visible and appeared in- credibly close (Fata Morgana if you are a child or a poet, anomalous atmo- spheric refraction if you are a scientist). On those mornings I would try to find a sandalo (a small gondola) and, accompanied by a friend, I would 3 4 BIOGRAPHICAL MEMOIRS row standing on the stern, Venetian style, from the Lido, where I lived, to the school in Venice, where I studied.
    [Show full text]
  • A Brief History of Nuclear Astrophysics
    A BRIEF HISTORY OF NUCLEAR ASTROPHYSICS PART I THE ENERGY OF THE SUN AND STARS Nikos Prantzos Institut d’Astrophysique de Paris Stellar Origin of Energy the Elements Nuclear Astrophysics Astronomy Nuclear Physics Thermodynamics: the energy of the Sun and the age of the Earth 1847 : Robert Julius von Mayer Sun heated by fall of meteors 1854 : Hermann von Helmholtz Gravitational energy of Kant’s contracting protosolar nebula of gas and dust turns into kinetic energy Timescale ~ EGrav/LSun ~ 30 My 1850s : William Thompson (Lord Kelvin) Sun heated at formation from meteorite fall, now « an incadescent liquid mass » cooling Age 10 – 100 My 1859: Charles Darwin Origin of species : Rate of erosion of the Weald valley is 1 inch/century or 22 miles wild (X 1100 feet high) in 300 My Such large Earth ages also required by geologists, like Charles Lyell A gaseous, contracting and heating Sun 푀⊙ Mean solar density : ~1.35 g/cc Sun liquid Incompressible = 4 3 푅 3 ⊙ 1870s: J. Homer Lane ; 1880s :August Ritter : Sun gaseous Compressible As it shrinks, it releases gravitational energy AND it gets hotter Earth Mayer – Kelvin - Helmholtz Helmholtz - Ritter A gaseous, contracting and heating Sun 푀⊙ Mean solar density : ~1.35 g/cc Sun liquid Incompressible = 4 3 푅 3 ⊙ 1870s: J. Homer Lane ; 1880s :August Ritter : Sun gaseous Compressible As it shrinks, it releases gravitational energy AND it gets hotter Earth Mayer – Kelvin - Helmholtz Helmholtz - Ritter A gaseous, contracting and heating Sun 푀⊙ Mean solar density : ~1.35 g/cc Sun liquid Incompressible = 4 3 푅 3 ⊙ 1870s: J.
    [Show full text]
  • A Bibliography of Publications By, and About, Charles Babbage
    A Bibliography of Publications by, and about, Charles Babbage Nelson H. F. Beebe University of Utah Department of Mathematics, 110 LCB 155 S 1400 E RM 233 Salt Lake City, UT 84112-0090 USA Tel: +1 801 581 5254 FAX: +1 801 581 4148 E-mail: [email protected], [email protected], [email protected] (Internet) WWW URL: http://www.math.utah.edu/~beebe/ 08 March 2021 Version 1.24 Abstract -analogs [And99b, And99a]. This bibliography records publications of 0 [Bar96, CK01b]. 0-201-50814-1 [Ano91c]. Charles Babbage. 0-262-01121-2 [Ano91c]. 0-262-12146-8 [Ano91c, Twe91]. 0-262-13278-8 [Twe93]. 0-262-14046-2 [Twe92]. 0-262-16123-0 [Ano91c]. 0-316-64847-7 [Cro04b, CK01b]. Title word cross-reference 0-571-17242-3 [Bar96]. 1 [Bab97, BRG+87, Mar25, Mar86, Rob87a, #3 [Her99]. Rob87b, Tur91]. 1-85196-005-8 [Twe89b]. 100th [Sen71]. 108-bit [Bar00]. 1784 0 [Tee94]. 1 [Bab27d, Bab31c, Bab15]. [MB89]. 1792/1871 [Ynt77]. 17th [Hun96]. 108 000 [Bab31c, Bab15]. 108000 [Bab27d]. 1800s [Mar08]. 1800s-Style [Mar08]. 1828 1791 + 200 = 1991 [Sti91]. $19.95 [Dis91]. [Bab29a]. 1835 [Van83]. 1851 $ $ $21.50 [Mad86]. 25 [O’H82]. 26.50 [Bab51a, CK89d, CK89i, She54, She60]. $ [Enr80a, Enr80b]. $27.95 [L.90]. 28 1852 [Bab69]. 1853 [She54, She60]. 1871 $ [Hun96]. $35.00 [Ano91c]. 37.50 [Ano91c]. [Ano71b, Ano91a]. 1873 [Dod00]. 18th $45.00 [Ano91c]. q [And99a, And99b]. 1 2 [Bab29a]. 1947 [Ano48]. 1961 Adam [O’B93]. Added [Bab16b, Byr38]. [Pan63, Wil64]. 1990 [CW91]. 1991 Addison [Ano91c]. Addison-Wesley [Ano90, GG92a]. 19th [Ano91c]. Addition [Bab43a]. Additions [Gre06, Gre01, GST01].
    [Show full text]
  • Booklet 2008-09.Indd
    The Shaw Prize The Shaw Prize is an international award to honour individuals who are currently active in their respective fields and who have achieved distinguished and significant advances, who have made outstanding contributions in culture and the arts, or who in other domains have achieved excellence. The award is dedicated to furthering societal progress, enhancing quality of life, and enriching humanity’s spiritual civilization. Preference will be given to individuals whose significant work was recently achieved. Founder's Biographical Note The Shaw Prize was established under the auspices of Mr Run Run Shaw. Mr Shaw, born in China in 1907, is a native of Ningbo County, Zhejiang Province. He joined his brother’s film company in China in the 1920s. In the 1950s he founded the film company Shaw Brothers (Hong Kong) Limited in Hong Kong. He has been Executive Chairman of Television Broadcasts Limited in Hong Kong since the 1970s. Mr Shaw has also founded two charities, The Sir Run Run Shaw Charitable Trust and The Shaw Foundation Hong Kong, both dedicated to the promotion of education, scientific and technological research, medical and welfare services, and culture and the arts. ~ 1 ~ Message from the Chief Executive I am delighted to congratulate the six distinguished scientists who receive this year’s Shaw Prize. Their accomplishments enrich human knowledge and have a profound impact on the advancement of science. This year, the Shaw Prize recognises remarkable achievements in the areas of astronomy, life science and medicine, and mathematical sciences. The exemplary work and dedication of this year’s recipients vividly demonstrate that constant drive for excellence will eventually bear fruit.
    [Show full text]
  • Quantum Interference Experiments with Large Molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger
    Quantum interference experiments with large molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger Citation: American Journal of Physics 71, 319 (2003); doi: 10.1119/1.1531580 View online: http://dx.doi.org/10.1119/1.1531580 View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/71/4?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Quantum interference and control of the optical response in quantum dot molecules Appl. Phys. Lett. 103, 222101 (2013); 10.1063/1.4833239 Communication: Momentum-resolved quantum interference in optically excited surface states J. Chem. Phys. 135, 031101 (2011); 10.1063/1.3615541 Theory Of Interference Of Large Molecules AIP Conf. Proc. 899, 167 (2007); 10.1063/1.2733089 Interference with correlated photons: Five quantum mechanics experiments for undergraduates Am. J. Phys. 73, 127 (2005); 10.1119/1.1796811 Erratum: “Quantum interference experiments with large molecules” [Am. J. Phys. 71 (4), 319–325 (2003)] Am. J. Phys. 71, 1084 (2003); 10.1119/1.1603277 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 128.118.49.21 On: Tue, 23 Dec 2014 19:02:58 Quantum interference experiments with large molecules Olaf Nairz,a) Markus Arndt, and Anton Zeilingerb) Institut fu¨r Experimentalphysik, Universita¨t Wien, Boltzmanngasse 5, A-1090 Wien, Austria ͑Received 27 June 2002; accepted 30 October 2002͒ Wave–particle duality is frequently the first topic students encounter in elementary quantum physics. Although this phenomenon has been demonstrated with photons, electrons, neutrons, and atoms, the dual quantum character of the famous double-slit experiment can be best explained with the largest and most classical objects, which are currently the fullerene molecules.
    [Show full text]
  • “A Valuable Monument of Mathematical Genius”\Thanksmark T1: the Ladies' Diary (1704–1840)
    Historia Mathematica 36 (2009) 10–47 www.elsevier.com/locate/yhmat “A valuable monument of mathematical genius” ✩: The Ladies’ Diary (1704–1840) Joe Albree ∗, Scott H. Brown Auburn University, Montgomery, USA Available online 24 December 2008 Abstract Our purpose is to view the mathematical contribution of The Ladies’ Diary as a whole. We shall range from the state of mathe- matics in England at the beginning of the 18th century to the transformations of the mathematics that was published in The Diary over 134 years, including the leading role The Ladies’ Diary played in the early development of British mathematics periodicals, to finally an account of how progress in mathematics and its journals began to overtake The Diary in Victorian Britain. © 2008 Published by Elsevier Inc. Résumé Notre but est de voir la contribution mathématique du Journal de Lady en masse. Nous varierons de l’état de mathématiques en Angleterre au début du dix-huitième siècle aux transformations des mathématiques qui a été publié dans le Journal plus de 134 ans, en incluant le principal rôle le Journal de Lady joué dans le premier développement de périodiques de mathématiques britanniques, à finalement un compte de comment le progrès dans les mathématiques et ses journaux a commencé à dépasser le Journal dans l’Homme de l’époque victorienne la Grande-Bretagne. © 2008 Published by Elsevier Inc. Keywords: 18th century; 19th century; Other institutions and academies; Bibliographic studies 1. Introduction Arithmetical Questions are as entertaining and delightful as any other Subject whatever, they are no other than Enigmas, to be solved by Numbers; .
    [Show full text]
  • Helmholtz's Dissonance Curve
    Tuning and Timbre: A Perceptual Synthesis Bill Sethares IDEA: Exploit psychoacoustic studies on the perception of consonance and dissonance. The talk begins by showing how to build a device that can measure the “sensory” consonance and/or dissonance of a sound in its musical context. Such a “dissonance meter” has implications in music theory, in synthesizer design, in the con- struction of musical scales and tunings, and in the design of musical instruments. ...the legacy of Helmholtz continues... 1 Some Observations. Why do we tune our instruments the way we do? Some tunings are easier to play in than others. Some timbres work well in certain scales, but not in others. What makes a sound easy in 19-tet but hard in 10-tet? “The timbre of an instrument strongly affects what tuning and scale sound best on that instrument.” – W. Carlos 2 What are Tuning and Timbre? 196 384 589 amplitude 787 magnitude sample: 0 10000 20000 30000 0 1000 2000 3000 4000 time: 0 0.23 0.45 0.68 frequency in Hz Tuning = pitch of the fundamental (in this case 196 Hz) Timbre involves (a) pattern of overtones (Helmholtz) (b) temporal features 3 Some intervals “harmonious” and others “discordant.” Why? X X X X 1.06:1 2:1 X X X X 1.89:1 3:2 X X X X 1.414:1 4:3 4 Theory #1:(Pythagoras ) Humans naturally like the sound of intervals de- fined by small integer ratios. small ratios imply short period of repetition short = simple = sweet Theory #2:(Helmholtz ) Partials of a sound that are close in frequency cause beats that are perceived as “roughness” or dissonance.
    [Show full text]
  • Neural Tracking of the Musical Beat Is Enhanced by Low-Frequency Sounds
    Neural tracking of the musical beat is enhanced by low-frequency sounds Tomas Lenca, Peter E. Kellera, Manuel Varleta, and Sylvie Nozaradana,b,c,1 aMARCS Institute for Brain, Behaviour, and Development, Western Sydney University, Penrith, NSW 2751, Australia; bInstitute of Neuroscience (IONS), Université Catholique de Louvain, 1200 Woluwe-Saint-Lambert, Belgium; and cInternational Laboratory for Brain, Music, and Sound Research (BRAMS), Département de Psychologie, Faculté des Arts et des Sciences, Université de Montréal, Montréal, QC H3C 3J7, Canada Edited by Dale Purves, Duke University, Durham, NC, and approved June 28, 2018 (received for review January 24, 2018) Music makes us move, and using bass instruments to build the content (8, 9). Bass sounds are also crucial in music that en- rhythmic foundations of music is especially effective at inducing courages listeners to move (10, 11). people to dance to periodic pulse-like beats. Here, we show that There has been a recent debate as to whether evolutionarily this culturally widespread practice may exploit a neurophysiolog- shaped properties of the auditory system lead to superior tem- ical mechanism whereby low-frequency sounds shape the neural poral encoding for bass sounds (12, 13). One study using elec- representations of rhythmic input by boosting selective locking to troencephalography (EEG) recorded brain responses elicited by the beat. Cortical activity was captured using electroencephalog- misaligned tone onsets in an isochronous sequence of simulta- raphy (EEG) while participants listened to a regular rhythm or to a neous low- and high-pitched tones (12). Greater sensitivity to the relatively complex syncopated rhythm conveyed either by low temporal misalignment of low tones was observed when they tones (130 Hz) or high tones (1236.8 Hz).
    [Show full text]