DOCSLIB.ORG

Craig Interpolation and Proof Manipulation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Craig Interpolation and Proof Manipulation Craig Interpolation and Proof Manipulation Theory and Applications to Model Checking Doctoral Dissertation submitted to the Faculty of Informatics of the Università della Svizzera Italiana in partial fulfillment of the requirements for the degree of Doctor of Philosophy presented by Simone Fulvio Rollini under the supervision of Prof. Natasha Sharygina February 2014 Dissertation Committee Prof. Rolf Krause Università della Svizzera Italiana, Switzerland Prof. Evanthia Papadopoulou Università della Svizzera Italiana, Switzerland Prof. Roberto Sebastiani Università di Trento, Italy Prof. Ofer Strichman Technion, Israel Dissertation accepted on 06 February 2014 Prof. Natasha Sharygina Prof. Igor Pivkin Prof. Stefan Wolf i I certify that except where due acknowledgement has been given, the work pre- sented in this thesis is that of the author alone; the work has not been submitted previously, in whole or in part, to qualify for any other academic award; and the content of the thesis is the result of work which has been carried out since the offi- cial commencement date of the approved research program. ii Abstract Model checking is one of the most appreciated methods for automated formal veri- fication of software and hardware systems. The main challenge in model checking, i.e. scalability to complex systems of extremely large size, has been successfully ad- dressed by means of symbolic techniques, which rely on an efficient representation and manipulation of the systems based on first order logic. Symbolic model checking has been considerably enhanced with the introduction in the last years of Craig interpolation as a means of overapproximation. Interpolants can be efficiently computed from proofs of unsatisfiability based on their structure. A number of algorithms are available to generate different interpolants from the same proof; additional interpolants can be obtained by turning a proof into another proof of unsatisfiability of the same formula using transformation techniques. Interpolants are thus not unique, and it is fundamental to understand which inter- polants have the highest quality, resulting in an optimal verification performance; it is an open problem to determine what features determine the quality of interpolants, and how they are connected with the effectiveness in verification. The goal of this thesis is to identify aspects that make interpolants good, and to develop new techniques that guide the generation of interpolants in order to improve the performance of model checking approaches. We contribute to the state-of-the-art by providing a characterization of quality in terms of semantic and syntactic features, such as logical strength, size, presence of quantifiers. We present a family of algorithms that generalize existing techniques and are able to produce interpolants of different structure and strength, with and without quantifiers, from the same proof. These algorithms are examined in the context of various model checking applications, where collections of interdependent interpolants satisfying particular properties are needed; we formally analyze the re- lationships among the properties and derive necessary and sufficient conditions on the applicability of the algorithms. We introduce a framework for proof manipulation; it includes a method to over- come limitations in existing interpolation algorithms for first order theories, as well as a set of compression algorithms, which, reducing the size of proofs, consequently iii iv reduce the size of interpolants generated from them. Finally, we provide experimental evidence that size and logical strength have a significant impact on verification: small interpolants improve the verification per- formance, while stronger or weaker interpolants are beneficial in different model checking applications. Interpolants are generated from proofs, as produced by logic solvers. As a sec- ondary line of research, we developed and successfully tested a hybrid propositional satisfiability solver built on a model-based stochastic technique known as cross- entropy method. Contents Contents iv 1 Introduction 1 1.1 Symbolic Model Checking . .3 1.2 SAT and SMT Solving . .4 1.2.1 Stochastic Techniques for Satisfiability . .5 1.3 Interpolation-Based Model Checking . .6 1.3.1 Interpolants Quality: Strength and Structure . .7 1.3.2 Interpolation Properties in Model Checking . .8 1.4 Resolution Proof Manipulation . 10 1.4.1 Proof Compression . 10 1.4.2 Enabling Interpolation in SMT . 11 1.5 Thesis Outline . 12 2 Hybrid Propositional Satisfiability 15 2.1 Satisfiability and SAT Solving . 16 2.1.1 DPLL and SLS . 16 2.2 A Cross-Entropy Based Approach to Satisfiability . 21 2.2.1 Cross-Entropy for Optimization . 22 2.2.2 The CROiSSANT Approach . 23 2.2.3 Experimental Results . 30 2.2.4 Related Work . 32 2.2.5 Summary and Future Developments . 33 3 Craig Interpolation in Model Checking 35 3.1 Interpolation in Symbolic Model Checking . 36 3.1.1 Interpolation, BMC and IC3 . 37 3.2 Interpolants Quality . 40 3.3 Generation of Interpolants . 41 v vi Contents 3.3.1 Craig Interpolation . 41 3.3.2 Interpolation Systems . 44 3.3.3 Interpolation in Arbitrary First Order Theories . 48 3.3.4 Interpolation in SAT . 51 3.3.5 Interpolation in SMT . 56 3.4 Theory Labeled Interpolation Systems . 58 3.4.1 Interpolant Strength in SMT . 61 3.4.2 Interpolation in Difference Logic . 63 3.4.3 Summary and Future Developments . 65 3.5 A Parametric Interpolation Framework for First Order Theories . 66 3.5.1 A Parametric Interpolation Framework . 67 3.5.2 Interpolation in First Order Systems . 71 3.5.3 Interpolation in the Hyper-Resolution System . 76 3.5.4 Related Work . 83 3.5.5 Summary and Future Developments . 83 3.6 Impact of Interpolant Strength and Structure . 85 3.6.1 PeRIPLO . 86 3.6.2 Function Summaries in Bounded Model Checking . 87 3.6.3 Experimental Evaluation . 89 3.6.4 Summary and Future Developments . 92 4 Interpolation Properties in Model Checking 95 4.1 Interpolation Systems . 97 4.1.1 Collectives . 97 4.2 Collectives of Interpolation Systems . 99 4.2.1 Collectives of Single Systems . 99 4.2.2 Collectives of Families of Systems . 101 4.3 Collectives of Labeled Interpolation Systems . 107 4.3.1 Collectives of Families of LISs . 108 4.3.2 Collectives of Single LISs . 124 4.4 Collectives of Theory Labeled Interpolation Systems . 126 4.4.1 Collectives of Families and of Single -LISs . 127 4.5 Summary and Future Developments . .T . 130 5 Proof Manipulation 133 5.1 Resolution Proofs . 134 5.2 The Local Transformation Framework . 136 5.2.1 Extension to Resolution Proof DAGs . 137 5.2.2 Soundness of the Local Transformation Framework . 139 vii Contents 5.2.3 A Transformation Meta-Algorithm . 143 5.3 Proof Compression . 144 5.3.1 Proof Redundancies . 146 5.3.2 Proof Regularity . 146 5.3.3 Proof Compactness . 154 5.3.4 Experiments on SMT Benchmarks . 160 5.3.5 Experiments on SAT Benchmarks . 163 5.4 Proof Transformation for Interpolation . 166 5.4.1 Pivot Reordering Algorithms . 167 5.4.2 SMT Solving and AB-Mixed Predicates . 169 5.4.3 Experiments on SMT Benchmarks . 173 5.4.4 Pivot Reordering for Propositional Interpolation . 174 5.5 Heuristics for the Proof Transformation Algorithms . 176 5.6 Related Work . 178 5.7 Summary and Future Developments . 180 6 Conclusions 183 Bibliography 187 viii Contents Chapter 1 Introduction In the last three decades there has been a considerable investment in the develop- ment of techniques and tools aimed at making the formal verification of hardware and software fully automated. Among various approaches, model checking is highly appreciated for its exhaustiveness and degree of automation: once a model (of hard- ware or software) and a specification of a property (desired behavior) are given, a tool can be run to explore all possible behaviors of the model, determining whether the property holds. The main difficulty in model checking is that for complex systems the size of the model often becomes too large to be handled in a reasonable amount of time. A remarkable improvement can be obtained by means of symbolic techniques: the model is encoded together with the negation of the property in a logic formula, satisfiable if and only if the specification is not met by the model. If this is the case, a logic solver can produce a satisfying assignment, representing a violating behavior; otherwise, a proof of unsatisfiability can be built as a witness of the validity of the property in the model. Symbolic model checking has been considerably enhanced with the introduction of Craig interpolation, as a means to perform a guided overapproximation of sets of states of the model. Interpolants can be efficiently computed from proofs of unsatisfiability; various algorithms are available to generate different interpolants from the same proof. Moreover, a given proof can be transformed into another proof of unsatisfiability of the same formula by means of proof manipulation techniques, consequently allowing additional interpolants. Interpolants are thus not unique, and it is fundamental to understand which in- terpolants result in an optimal verification performance: it is an open problem to determine what features determine the quality of interpolants, and how they are connected with the effectiveness in the verification. 1 2 This thesis focuses on the notion of quality of interpolants: the goal is to identify aspects that make interpolants good, and to develop new techniques that guide the generation of interpolants in order to improve the performance of model checking approaches. We contribute to the state-of-the-art in a number of ways. First, we provide a characterization of quality from both a semantic and a syntactic point of view, taking into account features as logical strength, size of formulae, and presence of quantifiers. Second, we present a family of algorithms that generalize existing techniques and are able to produce interpolants of different structure and strength, with and without quantifiers, from the same proof; they apply to arbitrary inference systems, in the context of both propositional logic and first order theories.
Load more

Recommended publications
  • Certification of First-Order Proofs in Classical and Intuitionistic Logics
    Certification of First-order proofs in classical and intuitionistic logics 1 Zakaria Chihani August 21, 2015 1This work has been funded by the ERC Advanced Grant ProofCert. Abstract The field of automated reasoning contains a plethora of methods and tools, each with its own language and its community, often evolving separately. These tools express their proofs, or some proof evidence, in different formats such as resolution refutations, proof scripts, natural deductions, expansion trees, equational rewritings and many others. The disparity in formats reduces communication and trust be- tween the different communities. Related efforts were deployed to fill the gaps in communication including libraries and languages bridging two or more tools. This thesis proposes a novel approach at filling this gap for first-order classical and intuitionistic logics. Rather than translating proofs written in various languages to proofs written in one chosen language, this thesis introduces a framework for describing the semantics of a wide range of proof evidence languages through a rela- tional specification, called Foundational Proof Certification (FPC). The description of the semantics of a language can then be appended to any proof evidence written in that language, forming a proof certificate, which allows a small kernel checker to verify them independently from the tools that created them. The use of seman- tics description for one language rather than proof translation from one language to another relieves one from the need to radically change the notion of proof. Proof evidence, unlike complete proof, does not have to contain all details. Us- ing proof reconstruction, a kernel checker can rebuild missing parts of the proof, allowing for compression and gain in storage space.
    [Show full text]
  • An Institutional View on Categorical Logic and the Curry-Howard-Tait-Isomorphism
    An Institutional View on Categorical Logic and the Curry-Howard-Tait-Isomorphism Till Mossakowski1, Florian Rabe2, Valeria De Paiva3, Lutz Schr¨oder1, and Joseph Goguen4 1 Department of Computer Science, University of Bremen 2 School of Engineering and Science, International University of Bremen 3 Intelligent Systems Laboratory, Palo Alto Research Center, California 4 Dept. of Computer Science & Engineering, University of California, San Diego Abstract. We introduce a generic notion of propositional categorical logic and provide a construction of an institution with proofs out of such a logic, following the Curry-Howard-Tait paradigm. We then prove logic-independent soundness and completeness theorems. The framework is instantiated with a number of examples: classical, intuitionistic, linear and modal propositional logics. Finally, we speculate how this framework may be extended beyond the propositional case. 1 Introduction The well-known Curry-Howard-Tait isomorphism establishes a correspondence between { propositions and types { proofs and terms { proof reductions and term reductions. Moreover, in this context, a number of deep correspondences between cate- gories and logical theories have been established (identifying `types' with `objects in a category'): conjunctive logic cartesian categories [19] positive logic cartesian closed categories [19] intuitionistic propositional logic bicartesian closed categories [19] classical propositional logic bicartesian closed categories with [19] ::-elimination linear logic ∗-autonomous categories [33] first-order logic hyperdoctrines [31] Martin-L¨of type theory locally cartesian closed categories [32] Here, we present work aimed at casting these correspondences in a common framework based on the theory of institutions. The notion of institution arose within computer science as a response to the population explosion among logics in use, with the ambition of doing as much as possible at a level of abstraction independent of commitment to any particular logic [16, 18].
    [Show full text]
  • Interpolation: Theory and Applications
    Interpolation: Theory and Applications Vijay D’Silva Google Inc., San Francisco UC Berkeley 2016 Wednesday, March 30, 16 1 A Brief History of Interpolation 2 Verification with Interpolants 3 Interpolant Construction 4 Further Reading and Research Wednesday, March 30, 16 Craig Interpolants For two formulae A and B such that A implies B B,aCraig interpolant is a formula I such that 1. A implies I, and I 2. I implies B, and 3. the non-logical symbols in I occur in A and in B. A P (P = Q)=Q = R = Q ^ ) ) ) ) Wednesday, March 30, 16 Reverse Interpolants or “Interpolants” For a contradiction A B,areverse interpolant is ^ a formula I such that B 1. A implies I, and 2. I B is a contradiction, and ^ I 3. the non-logical symbols in I occur in A and in B. Note: In classical logic, A = B is valid exactly ) A if A B is a contradiction. ^¬ In the verification literature, “interpolant” usually means “reverse interpolant.” Wednesday, March 30, 16 International Business Machines Corporation 2050 Rt 52 Hopewell Junction, NY 12533 845-892-5262 October 7, 2008 Dear Andreas, I would like to congratulate Cadence Research Labs on their 15th Anniversary. In these 15 years, Cadence Research Labs has worked at several frontiers of Electronic Design Automation. They focus on hard problems that when solved significantly push the state of the art forward. They found novel solutions to system, synthesis and formal verification problems. Formal verification is the process of exhaustively validating that a logic entity behaves correctly. In contrast to testing-based approaches, which may expose flaws though generally cannot yield a proof of correctness, the exhaustiveness of formal verification ensures that no flaw will be left unexposed.
    [Show full text]
  • Abstract Algebraic Logic an Introductory Chapter
    Abstract Algebraic Logic An Introductory Chapter Josep Maria Font 1 Introduction . 1 2 Some preliminary issues . 5 3 Bare algebraizability . 10 3.1 The equational consequence relative to a class of algebras . 11 3.2 Translating formulas into equations . 13 3.3 Translating equations into formulas . 15 3.4 Putting it all together . 15 4 The origins of algebraizability: the Lindenbaum-Tarski process . 18 4.1 The process for classical logic . 18 4.2 The process for algebraizable logics . 20 4.3 The universal Lindenbaum-Tarski process: matrix semantics . 23 4.4 Algebraizability and matrix semantics: definability . 27 4.5 Implicative logics . 29 5 Modes of algebraizability, and non-algebraizability . 32 6 Beyond algebraizability . 37 6.1 The Leibniz hierarchy . 37 6.2 The general definition of the algebraic counterpart of a logic . 45 6.3 The Frege hierarchy . 49 7 Exploiting algebraizability: bridge theorems and transfer theorems . 55 8 Algebraizability at a more abstract level . 65 References . 69 1 Introduction This chapter has been conceived as a brief introduction to (my personal view of) abstract algebraic logic. It is organized around the central notion of algebraizabil- ity, with particular emphasis on its connections with the techniques of traditional algebraic logic and especially with the so-called Lindenbaum-Tarski process. It Josep Maria Font Departament of Mathematics and Computer Engineering, Universitat de Barcelona (UB), Gran Via de les Corts Catalanes 585, E-08007 Barcelona, Spain. e-mail: [email protected] 1 2 Josep Maria Font goes beyond algebraizability to offer a general overview of several classifications of (sentential) logics—basically, the Leibniz hierarchy and the Frege hierarchy— which have emerged in recent decades, and to show how the classification of a logic into any of them provides some knowledge regarding its algebraic or its metalogical properties.
    [Show full text]
  • Combinatorial Flows and Proof Compression Lutz Straßburger
    Combinatorial Flows and Proof Compression Lutz Straßburger To cite this version: Lutz Straßburger. Combinatorial Flows and Proof Compression. [Research Report] RR-9048, Inria Saclay. 2017. hal-01498468 HAL Id: hal-01498468 https://hal.inria.fr/hal-01498468 Submitted on 30 Mar 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Combinatorial Flows and Proof Compression Lutz Straßburger RESEARCH REPORT N° 9048 March 2017 Project-Team Parsifal ISSN 0249-6399 ISRN INRIA/RR--9048--FR+ENG Combinatorial Flows and Proof Compression Lutz Straßburger Project-Team Parsifal Research Report n° 9048 — March 2017 — 16 pages Abstract: This paper introduces the notion of combinatorial flows as a generalization of combinatorial proofs that also includes cut and substitution as methods of proof compression. We show a normalization procedure for combinatorial flows, and how syntactic proofs in sequent calculus, deep inference, and Frege systems are translated into combinatorial flows and vice versa. Key-words: Combinatorial flows, deep inference, proof compression, cut elimination, substitution elimination RESEARCH CENTRE SACLAY – ÎLE-DE-FRANCE 1 rue Honoré d’Estienne d’Orves Bâtiment Alan Turing Campus de l’École Polytechnique 91120 Palaiseau Fleuves combinatoires et compression des preuves Resum´ e´ : Cet article introduit la notion de fleuves combinatoires comme gen´ eralisation´ des preuves combinatoires qui comprend egalement´ la coupure et la substitution comme methodes´ de compression des preuves.
    [Show full text]
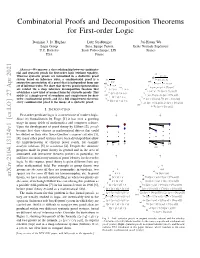
  • Combinatorial Proofs and Decomposition Theorems for First
    Combinatorial Proofs and Decomposition Theorems for First-order Logic Dominic J. D. Hughes Lutz Straßburger Jui-Hsuan Wu Logic Group Inria, Equipe Partout Ecole Normale Sup´erieure U.C. Berkeley Ecole Polytechnique, LIX France USA France Abstract—We uncover a close relationship between combinato- rial and syntactic proofs for first-order logic (without equality). ax ⊢ pz, pz Whereas syntactic proofs are formalized in a deductive proof wk system based on inference rules, a combinatorial proof is a ax ⊢ pw, pz, pz ⊢ p,p wk syntax-free presentation of a proof that is independent from any wk ⊢ pw, pz, pz, ∀y.py set of inference rules. We show that the two proof representations ⊢ p,q,p ∨ ∨ ax ⊢ pw, pz, pz ∨ (∀y.py) are related via a deep inference decomposition theorem that ⊢ p ∨ q,p ⊢ p,p ∃ ∧ ⊢ pw, pz, ∃x.(px ∨ (∀y.py)) establishes a new kind of normal form for syntactic proofs. This ⊢ (p ∨ q) ∧ p,p,p ∀ yields (a) a simple proof of soundness and completeness for first- ctr ⊢ pw, ∀y.py, ∃x.(px ∨ (∀y.py)) ⊢ (p ∨ q) ∧ p,p ∨ order combinatorial proofs, and (b) a full completeness theorem: ∨ ⊢ pw ∨ (∀y.py), ∃x.(px ∨ (∀y.py)) ⊢ ((p ∨ q) ∧ p) ∨ p ∃ every combinatorial proof is the image of a syntactic proof. ⊢ ∃x.(px ∨ (∀y.py)), ∃x.(px ∨ (∀y.py)) ctr ⊢ ∃x.(px ∨ (∀y.py)) I. INTRODUCTION First-order predicate logic is a cornerstone of modern logic. ↓ ↓ Since its formalisation by Frege [1] it has seen a growing usage in many fields of mathematics and computer science. Upon the development of proof theory by Hilbert [2], proofs became first-class citizens as mathematical objects that could be studied on their own.
    [Show full text]
  • What Is a Logic? Till Mossakowski Joseph Goguen R˘Azvan Diaconescu Andrzej Tarlecki October 16, 2004
    What is a Logic? Till Mossakowski Joseph Goguen R¸azvan Diaconescu Andrzej Tarlecki October 16, 2004 TODO: Joseph: Our cardinality spectra generalize traditional cardinality properties from func- tions of signature cardinality, to functors of signature isomorphism type. TODO: Replace diagram by equations? Vertical spaces as small as possible; combine paragraphs when possible; reduce model theory details; be cruel with references, use smaller font, less space between refs; better explanations of key material for main point. TODO: Razvan: mention new results for classical logics obtained by institution theory: Craig interpolation of some fragments of classical logic (see Studia Logica paper). 1 Introduction Logic is often informally described as the study of sound reasoning. As such, it plays a crucial role in several areas of mathematics (especially foundations) and of computer science (especially formal methods), as well as in other ¯elds, such as analytic philosophy and formal linguistics. In an enormous development beginning in the late 19th century, it has been found that a wide variety of di®erent principles are needed for sound reasoning in di®erent domains, and \a logic" has come to mean a set of principles for some form of sound reasoning. But in a subject the essence of which is formalization, it is embarrassing that there is no widely acceptable formal de¯nition of \a logic". It is clear that two key problems here are to de¯ne what it means for two presentations of a logic to be equivalent, and to provide e®ective means to demonstrate equivalence and inequivalence. This essay addresses these problems using the notion of \institution", which arose within computer science in response to the recent population explosion among logics in use there, with the ambition of doing as much as possible at a level of abstraction independent of commitment to any particular logic [16, 19].
    [Show full text]
  • Harmonious Logic: Craig's Interpolation Theorem and Its
    Harmonious Logic Harmonious Logic: Craig’s Interpolation Theorem and its Descendants Solomon Feferman For Bill Craig, with great appreciation for his fundamental contributions to our subject, and for his perennially open, welcoming attitude and fine personality that enhances every encounter. Abstract: Though deceptively simple and plausible on the face of it, Craig’s interpolation theorem (published 50 years ago) has proved to be a central logical property that has been used to reveal a deep harmony between the syntax and semantics of first order logic. Craig’s theorem was generalized soon after by Lyndon, with application to the characterization of first order properties preserved under homomorphism. After retracing the early history, this article is mainly devoted to a survey of subsequent generalizations and applications, especially of many-sorted interpolation theorems. Attention is also paid to methodological considerations, since the Craig theorem and its generalizations were initially obtained by proof-theoretic arguments while most of the applications are model-theoretic in nature. The article concludes with the role of the interpolation property in the quest for “reasonable” logics extending first-order logic within the framework of abstract model theory. Key words: Craig’s theorem, interpolation theorems, preservation theorems, many- sorted languages, extensions of first-order logic, abstract model theory. 1. Craig’s Interpolation Theorem. A common statement of Craig’s theorem (initially referred to by him as a lemma) goes as follows: Suppose | ϕ(R, S) → ψ(S, T). Then there is a θ(S) such that | ϕ(R, S) → θ(S) and | θ(S) → ψ(S, T). 1 Here | is validity in classical first order logic with equality (FOL), ϕ, ψ, θ are sentences, and R, S, and T are sequences of relation symbols for which the sequence S is non-empty.
    [Show full text]
  • Algorithmic Structuring and Compression of Proofs (ASCOP)
    Project Presentation: Algorithmic Structuring and Compression of Proofs (ASCOP) Stefan Hetzl Institute of Discrete Mathematics and Geometry Vienna University of Technology Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria [email protected] Abstract. Computer-generated proofs are typically analytic, i.e. they essentially consist only of formulas which are present in the theorem that is shown. In contrast, mathematical proofs written by humans almost never are: they are highly structured due to the use of lemmas. The ASCOP-project aims at developing algorithms and software which structure and abbreviate analytic proofs by computing useful lemmas. These algorithms will be based on recent groundbreaking results estab- lishing a new connection between proof theory and formal language the- ory. This connection allows the application of efficient algorithms based on formal grammars to structure and compress proofs. 1 Introduction Proofs are the most important carriers of mathematical knowledge. Logic has endowed us with formal languages for proofs which make them amenable to al- gorithmic treatment. From the early days of automated deduction to the current state of the art in automated and interactive theorem proving we have witnessed a huge increase in the ability of computers to search for, formalise and work with proofs. Due to the continuing formalisation of computer science (e.g. in areas such as hardware and software verification) the importance of formal proofs will grow further. Formal proofs which are generated automatically are usually difficult or even impossible to understand for a human reader. This is due to several reasons: one is a potentially extreme length as in the well-known cases of the four colour theorem or the Kepler conjecture.
    [Show full text]
  • The Craig Interpolation Theorem in Abstract Model Theory
    Synthese (2008) 164:401–420 DOI 10.1007/s11229-008-9357-z The Craig Interpolation Theorem in abstract model theory Jouko Väänänen Received: 12 March 2008 / Accepted: 2 June 2008 / Published online: 1 July 2008 © The Author(s) 2008 Abstract The Craig Interpolation Theorem is intimately connected with the emergence of abstract logic and continues to be the driving force of the field. I will argue in this paper that the interpolation property is an important litmus test in abstract model theory for identifying “natural,” robust extensions of first order logic. My argu- ment is supported by the observation that logics which satisfy the interpolation property usually also satisfy a Lindström type maximality theorem. Admittedly, the range of such logics is small. Keywords Interpolation · Abstract logic · Generalized quantifier · Infinitary language 1 Introduction Abstract model theory studies general model theoretic properties of extensions of first order logic obtained by adding generalized quantifiers, infinitary operations, or higher order quantifiers. We will not define the concept of an abstract logic here, as the def- inition is quite long and the intuitive concept suffices for this survey. The intuitive concept is the following: In first order logic every sentence ϕ has an associated class Kϕ of models, namely the class of models of ϕ. If we forget about the sentences ϕ we can think of first order logic simply as a collection L of model classes K . First order logic has thus become an abstract logic. More generally an abstract logic is a collec- tion L of model classes K satisfying some natural axioms such as every model class J.
    [Show full text]
  • What We Know and Don't Know About Craig Interpolation And
    What we know and don’t know about Craig Interpolation and Propositional Dynamic Logic. Malvin Gattinger ILLC, Amsterdam 2016-12-06 Department of Philosophy Peking University Based on many discussions with Yde Venema. Disclaimer I don’t know whether PDL has Craig Interpolation. (I don’t know whether)2 PDL has Craig Interpolation. I don’t know whether I know whether PDL has Craig Interpolation. Contents Craig-Interpolation Propositional Dynamic Logic Craig Interpolation for PDL Craig-Interpolation William Craig (November 13, 1918 – January 13, 2016) I born in Nürnberg I first proved Interpolation for first-order logic in 1957 Interpolation in Natural Language I If god exists, then the world will never end and all humans and cats will live forever. ⇒ If god exists and I am a cat, then I will live forever. © “Simon’s Cat” Interpolation in Natural Language II If god exists, then the world will never end and all humans and cats will live forever. ⇒ If god exists, then all cats will live forever. ⇒ If god exists and I am a cat, then I will live forever. © “Simon’s Cat” Craig-Interpolation: Definition Given: I Λ – logic as set of formulas, given by semantics or proof system I L(ϕ) – language of a formula I e.g. proposition letters: L(p → ((r ∨ p) ∧ q)) = {p, q, r} Definition Λ has Craig Interpolation iff for any ϕ → ψ ∈ Λ, there is a µ s.t.: I L(µ) ⊆ L(ϕ) ∩ L(ψ), I ϕ → µ ∈ Λ I and µ → ψ ∈ Λ. Then call µ an interpolant for ϕ → ψ.
    [Show full text]
  • Craig Interpolation in Displayable Logics
    Craig Interpolation in Displayable Logics James Brotherston1 and Rajeev Gor´e2 1 Dept. of Computing, Imperial College London [email protected] 2 School of Computer Science, ANU Canberra [email protected] Abstract. We give a general proof-theoretic method for establishing Craig interpolation for displayable logics, based upon an analysis of the individual proof rules of their display calculi. Using this uniform method, we establish interpolation for a spectrum of display calculi differing in their structural rules, including those for multiplicative linear logic, mul- tiplicative additive linear logic and ordinary classical logic. Our analysis at the level of proof rules also provides new insights into the reasons why interpolation fails, or seems likely to fail, in many substruc- tural logics. Specifically, we identify contraction as being particularly problematic for interpolation except in special circumstances. 1 Introduction I believe or hope that Display logic can be used as a basis for establishing an interpolation theorem; but that remains to be seen. Nuel D. Belnap, Display Logic [1], 1982 Craig’s original interpolation theorem for first-order logic [5] states that for any provable entailment F ` G between formulas, an “intermediate formula” or interpolant I can be found such that both F ` I and I ` G are provable and every nonlogical symbol occurring in I occurs in both F and G. This seemingly innocuous property turns out to have considerable mathematical significance be- cause Craig interpolation is intimately connected with consistency, compactness and definability (see [7] for a survey). In computer science, it plays an important rˆole in settings in which modular decomposition of complex theories is a con- cern.
    [Show full text]