DOCSLIB.ORG

Tumbling Asteroids

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Tumbling Asteroids Tumbling Asteroids Alan W. I]arris A4S 183-501, .Jet l’ropul.vim l.ahmtory l’clsdwl, CA, 91109 Submitted as a Note to lcarus July 31, 1993 S Manl]script pages 1 Figlll”e Suggest cd running head: ~iumbling Asteroids Send corrcspondcncc to: Alan W. 1 ]arris Al\ S’1’RAC’l’ l]urns and Safrcmov (A40n. Not, 1/, As(wtr. ,Voc. 16S, 403-411, 1973) cstimalcd the damping timescalc of rotational \vobblc for asteroids, and concluded that all askxoid rotations then knowm should bc damped to a state of plincipal-axis rotation about tbc axis of maxilnunl mmncn( of inertia, I have rc-examined this c]ucstion in the light of some more rcccnt]y dctcrmincd case.s of very slo~v rotation rates, and find that for several asteroids, the damping tinmcalc is cxpcctcd to bc considerably longer tba]l the agc of the solar systcm, implying that these objects may t’cry \vcll exhibit non-principal axis rotation: ~~obblc, or in cxt rcmc cases, the appearance of “tumbling” in space. I’crhaps most notable in this group is the asteroid 4179 ‘J’outatis, Both radar observations (Os(ro, personal corllr]lll]~icatioll) and lightcurvc observations (Barucci, Spcnccr, personal communications) .suggcst that Toutatis may indeed bc in a more complex state of rotational motion than simple principal axis rotation 1 mention several other examples of objects which might bc cxpcctcd to bc in similar s[atcs, and a couple examples of ligbtcurvc observations of such objects that appear to support that conclusicm. MOSI of our knotvlcdgc regarding the rotalion states of as(croids comes from photometric lightcur~’cs. ‘1’o date periods have been dctcrmincd for more than 600 otjccts, }’or about 100 of these, the lightcurvcs arc so fflcicntly dclailcd and cover cllough cyc]cs to support the cor[clusio[t that the rotalion is constant about the axis of rnaxill]unl moment of incttia. I’hat is, the lightcurvc is strictly periodic with a single rotation frequency (l)lus harmonics), cxccpt for ~’ariations attributable to changing aspect of illumination and vic\ving. Since it is generally bclicvcd that the rotational motion is the result of collisional proccsscs, and among smaller asteroids involves catastrophic disruptions from larger parent bodies, onc would expect that o] isinal spin states involved large amplitude wobbles, rcsolting in a complex “tumbling” t}~c of nlotion, such as appears to bc the case for the nucleus of (omct P/lla]lcy (Peale and I,issaucr 1989; Ilclton 1991). IIurns and Safronov (1973) examined tbc rate of dissipation of rotational culcrgy as a result the stress-strain within an asteroid tvhich arises from non-principal axis rotation Such motion is cxaclly analogous to the I:arth’s C%andlcr Wobble, and as with the Iiatlh, is damped duc to stress-strain hyslcrcsis willlirl the body, “1’hcy derive the follolving expression for tk time scale T of damping of the ~vobb]c to a state of principal axis rotation: T -- pQ/(pK32r2m3), where p is the rigidity of the material composing the asteroid, Q is IIIC quality factor (ratio oft hc energy contained in the oscillation to Ibc energy lost pcr cycle), p is the bulk density of the body, K32 is a numerical factor relating to IIIC irregularity of tbc body ranging from -0.01 for a ncar]y-spherical onc to -0,1 for a highly elongate or oblatc OIIC, r is tbc mean radius of the asteroid, and (o is the angular frequency of rotation, Burns and Safronov compute damping timcscalcs for 4 example asteroids, obtailting timcscalcs ranging from -lOs years to -108 years, I’hus Ihcy concluded that probably all observed asteroids arc in a state of damped rotational motion, At the time that they made tbcir analysis, the lon~cst rotaticm period “known” (McAdoo and Burns 1973) was 18.813 hours (for 5321 Icrculina; that reported value subsequently turned out to bc wro]~g), so in the contcx( of all rotatio]~s known tbcn, tbcir conclusion was quite il refutable, c~w allowing for a generous range of uncertainty of the parameters involved, most notably }(Q, It is clear ho~vcvcr, duc to the factors rb3, the damping, time could be very long for small asteroids }vith very long rotation periods, ‘1’his was pointed out by McAdoo and Burns (1974), but pro]nptly forgotten by most cvcr~’one, myself illcludcd, At the urging of S, J, Ostro (personal communicant ion), 1 rcconsidcrcd the timcscalcs of wobble damping for tbc nolv much larger data set of asteroid rotations, which include several examples of many-day rotation periods, l’hc case in point \vas tbc asteroid 4179 “1’outatis, which was imaged on many days with radar by Ostro and his collaborators, and was observed pbotoclcctrically \’cry cxtcnsivc]y ot’cr t}vo months from Dcccmbcr 1992 through January ] 9°3 (]]arLICCl, Spcnccr, persona] co]]~][illllicatiolls), Prclimiltary cxamina[ion of both the radar and optical ciala indicate that ‘1 ‘outatis is a very irregular object ~~itb a very long rotation “period”, and suggest that I’outatis’ rotatio]m] motion is more complex than simple principal axis rotation A quick substitution of the physical parameters appropriate for ‘1’outatis (rotation period ~-7.5 days, r -2 kn~, K32 - 0.05), and adopting Bum’ and x. (,,.1, ? Safronov’s WIUCS of all the other parameters, YICICJS a timcscale of -1.5 x 10’2 years. ‘1’hus onc should cxpwl that ‘J’outatis’ rotational motion is no[ simple, even if it is as old as the agc of the solar systcm. ~onsidcril]g that asteroids only a fcw kilometers in diameter arc cxpcctcd to have a collisional lifctin~cs of only a small fraction of the agc of the solar systcm (probably <108 years), it is even mote likely that ‘1’outatis’ rotational \vobblc is undamped, Iollowin~ the rcalimtion that there arc now cases where the wobble damping time is cxpcctcd to bc long comprrrcct to (1IC ages of the asteroids, 1 rc-cvaluatccl the above ccplation in greater detail, using more current estimates for the other parameters. I C11OSC p = 2.0 al)d pQ = S x 10’2, based on estimates of these parameters for I’hobos, the only small body in the relevant siz.c rang,c for which \vc have estimates of these properties. ‘1’hc cstinlatc of jIQ for I’}~obos is based on the observed eccentricity of its orbit about Mars, and a plausib]c past orbital history under tidal evolution (Yodcr 1982). Burns and Safronov chose a value of itQ = 3 x 10]4, which would bc appropriate for a solid, non-porous rock, and is likely too high, but was appropriately chosen to obtain a firm upper limit in their work Peale and I,issaucr (1989) sugucst that p c: 10’0 and Q <100 might bc appropriate for ~omct 12 1 Iallcy. I’hus I conclude that pQ probably lies ~vithin a factor of 10 of the assumed value of 5 x 10 , and certainly wit hin a factor of 100. ‘J’hc uncertainty in p probably dots not cxcccd a factor of 1.5, so the error bud~ct is dominated by pQ, I;vcn the range of vahm possible of K32, from 0.01 to 0.1, is hardly significant compared to the uncertainty in pQ. ‘1’hus in the relation below, I have adopted a uniform value of 0.03, even though onc could in principle c.stimatc values for each individual as[croid based on lightcurvc amplitude, Using these conslants, I derive the following relationship bctwccn rotation period P in hours, diameter D in km, and damping timcscalc ‘t in billions ofycars: }, ,. ]7 1)23T1/3, I’hc uncertainty in the constant is about a factor of 2,5, combining the unccr[ainties in all of the other parameters; that is, P = (7-40) D2’3 T} ’3. in }iig,urc J, 1 hal’c plotted solutions to the above relation for three vahrcs of ‘t on a plot of measured asteroid rotation rates vs., diarnctcrs. It has generally been claimed that most of the present asteroids, especially those s[tmllcr tl]all 100-200 km in diameter, arc not primordial, but rather arc the products of catastrophic disruptions. Such an event should “rc.set” the rotation state of tlic fragnlcnts, and especially il~ducc large \vobblc amplitudes. Rcccllt estimates of the collision energy threshold for catastrophic disruption as a function of size of the target body (lloLIscn C( al. 1991) imply that the cxpcctcd “age” of a SO km asteroid may bc – 10s years, and objects a fcw kn~ in diameter may survive only107 - . years, ‘1’hus in the figure, any object that falls below even the topmost line plotted should bc considered a candidate for non-principal axis rotation, and those below the bottom line arc almost ccrlain to bc in a state of large amplitude wobble, or “tumbling”. I have identified in the figure all of the objects that have estimated T <1 b,y. Note that the four objects, 3102 1981 QA, 4179 ‘1’outatis, 1220 Crocus, and 288 Glaukc, arc most cxtrcmc, having damping timcscalcs much longer than the agc of the solar systcm. As I have already noted, the obscrvatio]lal data on I’outatis is at least consis[cnt with, if not requiring, tumbling motion A major point of this note is to cncouragc observers to evaluate tllc availab]c data in the light of this prospect, of the other three objects, it can bc said that the cxisling data arc i]mtTcicnt to demonstrate non-principal axis rotation, but arc not inconsistent \vit}l that possibility (SCC Ilarris ef GI, 1992 for the lightcurvc of 3 102; Bin~.cl 1985 for 1220; and IIarris 1983 for 288), Moving up to the asteroids ~vith T -- 4,5 by., 887 Alinda was observed cxtcnsivcly during two apparitions, in 1969/70 and 1973/74, by Dunlap and I’aylor (1979), but again the overlap in covcragc was inadequate to make any definite statcrncnt about the prcsc]lcc or abscncc of wobble.
Load more

Recommended publications
  • Physical Properties of Near-Earth Asteroids
    Planet. Space Sci., Vol. 46, No. 1, pp. 47-74, 1998 Pergamon N~I1998 Elsevier Science Ltd All rights reserved. Printed in Great Britain 00324633/98 $19.00+0.00 PII: SOO32-0633(97)00132-3 Physical properties of near-Earth asteroids D. F. Lupishko’ and M. Di Martino’ ’ Astronomical Observatory of Kharkov State University, Sumskaya str. 35, Kharkov 310022, Ukraine ‘Osservatorio Astronomic0 di Torino, I-10025 Pino Torinese (TO), Italy Received 5 February 1997; accepted 20 June 1997 rather small objects, usually of the order of a few kilo- metres or less. MBAs of such sizes are generally not access- ible to ground-based observations. Therefore, when NEAs approach the Earth (at distances which can be as small as 0.01-0.02 AU and sometimes less) they give a unique chance to study objects of such small sizes. Some of them possibly represent primordial matter, which has preserved a record of the earliest stages of the Solar System evolution, while the majority are fragments coming from catastrophic collisions that occurred in the asteroid main- belt and could provide “a look” at the interior of their much larger parent bodies. Therefore, NEAs are objects of special interest for sev- eral reasons. First, from the point of view of fundamental science, the problems raised by their origin in planet- crossing orbits, their life-time, their possible genetic relations with comets and meteorites, etc. are closely connected with the solution of the major problem of “We are now on the threshold of a new era of asteroid planetary science of the origin and evolution of the Solar studies” System.
    [Show full text]
  • Observations from Orbiting Platforms 219
    Dotto et al.: Observations from Orbiting Platforms 219 Observations from Orbiting Platforms E. Dotto Istituto Nazionale di Astrofisica Osservatorio Astronomico di Torino M. A. Barucci Observatoire de Paris T. G. Müller Max-Planck-Institut für Extraterrestrische Physik and ISO Data Centre A. D. Storrs Towson University P. Tanga Istituto Nazionale di Astrofisica Osservatorio Astronomico di Torino and Observatoire de Nice Orbiting platforms provide the opportunity to observe asteroids without limitation by Earth’s atmosphere. Several Earth-orbiting observatories have been successfully operated in the last decade, obtaining unique results on asteroid physical properties. These include the high-resolu- tion mapping of the surface of 4 Vesta and the first spectra of asteroids in the far-infrared wave- length range. In the near future other space platforms and orbiting observatories are planned. Some of them are particularly promising for asteroid science and should considerably improve our knowledge of the dynamical and physical properties of asteroids. 1. INTRODUCTION 1800 asteroids. The results have been widely presented and discussed in the IRAS Minor Planet Survey (Tedesco et al., In the last few decades the use of space platforms has 1992) and the Supplemental IRAS Minor Planet Survey opened up new frontiers in the study of physical properties (Tedesco et al., 2002). This survey has been very important of asteroids by overcoming the limits imposed by Earth’s in the new assessment of the asteroid population: The aster- atmosphere and taking advantage of the use of new tech- oid taxonomy by Barucci et al. (1987), its recent extension nologies. (Fulchignoni et al., 2000), and an extended study of the size Earth-orbiting satellites have the advantage of observing distribution of main-belt asteroids (Cellino et al., 1991) are out of the terrestrial atmosphere; this allows them to be in just a few examples of the impact factor of this survey.
    [Show full text]
  • CURRICULUM VITAE, ALAN W. HARRIS Personal: Born
    CURRICULUM VITAE, ALAN W. HARRIS Personal: Born: August 3, 1944, Portland, OR Married: August 22, 1970, Rose Marie Children: W. Donald (b. 1974), David (b. 1976), Catherine (b 1981) Education: B.S. (1966) Caltech, Geophysics M.S. (1967) UCLA, Earth and Space Science PhD. (1975) UCLA, Earth and Space Science Dissertation: Dynamical Studies of Satellite Origin. Advisor: W.M. Kaula Employment: 1966-1967 Graduate Research Assistant, UCLA 1968-1970 Member of Tech. Staff, Space Division Rockwell International 1970-1971 Physics instructor, Santa Monica College 1970-1973 Physics Teacher, Immaculate Heart High School, Hollywood, CA 1973-1975 Graduate Research Assistant, UCLA 1974-1991 Member of Technical Staff, Jet Propulsion Laboratory 1991-1998 Senior Member of Technical Staff, Jet Propulsion Laboratory 1998-2002 Senior Research Scientist, Jet Propulsion Laboratory 2002-present Senior Research Scientist, Space Science Institute Appointments: 1976 Member of Faculty of NATO Advanced Study Institute on Origin of the Solar System, Newcastle upon Tyne 1977-1978 Guest Investigator, Hale Observatories 1978 Visiting Assoc. Prof. of Physics, University of Calif. at Santa Barbara 1978-1980 Executive Committee, Division on Dynamical Astronomy of AAS 1979 Visiting Assoc. Prof. of Earth and Space Science, UCLA 1980 Guest Investigator, Hale Observatories 1983-1984 Guest Investigator, Lowell Observatory 1983-1985 Lunar and Planetary Review Panel (NASA) 1983-1992 Supervisor, Earth and Planetary Physics Group, JPL 1984 Science W.G. for Voyager II Uranus/Neptune Encounters (JPL/NASA) 1984-present Advisor of students in Caltech Summer Undergraduate Research Fellowship Program 1984-1985 ESA/NASA Science Advisory Group for Primitive Bodies Missions 1985-1993 ESA/NASA Comet Nucleus Sample Return Science Definition Team (Deputy Chairman, U.S.
    [Show full text]
  • Binary Asteroids and the Formation of Doublet Craters
    ICARUS 124, 372±391 (1996) ARTICLE NO. 0215 Binary Asteroids and the Formation of Doublet Craters WILLIAM F. BOTTKE,JR. Division of Geological and Planetary Sciences, California Institute of Technology, Mail Code 170-25, Pasadena, California 91125 E-mail: [email protected] AND H. JAY MELOSH Lunar and Planetary Laboratory, University of Arizona, Tucson, Arizona 85721 Received April 29, 1996; revised August 14, 1996 found we could duplicate the observed fraction of doublet cra- At least 10% (3 out of 28) of the largest known impact craters ters found on Earth, Venus, and Mars. Our results suggest on Earth and a similar fraction of all impact structures on that any search for asteroid satellites should place emphasis Venus are doublets (i.e., have a companion crater nearby), on km-sized Earth-crossing asteroids with short-rotation formed by the nearly simultaneous impact of objects of compa- periods. 1996 Academic Press, Inc. rable size. Mars also has doublet craters, though the fraction found there is smaller (2%). These craters are too large and too far separated to have been formed by the tidal disruption 1. INTRODUCTION of an asteroid prior to impact, or from asteroid fragments dispersed by aerodynamic forces during entry. We propose that Two commonly held paradigms about asteroids and some fast rotating rubble-pile asteroids (e.g., 4769 Castalia), comets are that (a) they are composed of non-fragmented after experiencing a close approach with a planet, undergo tidal chunks of rock or rock/ice mixtures, and (b) they are soli- breakup and split into multiple co-orbiting fragments.
    [Show full text]
  • WG Photometry and Polarimetry of Asteroids
    PHOTOMETRY AND POLARIMETRY OF ASTEROIDS: IMPACT ON COLLABORATION Abstracts The International Workshop -2 80 0 60 2 40 4 20 6 Relative Magnitude Polarization Degree 0 8 10 -20 0 20 40 60 80 100 120 140 160 180 Phase Angle June 15–18, 2003, Kharkiv, Ukraine Organized by Research Institute of Astronomy of V. N. Karazin Kharkiv National University, Ukrainian Astronomical Association Ministry of Education and Science of Ukraine Sponsored by Kharkiv City Charity Fund “AVEC” PHOTOMETRY AND POLARIMETRY OF ASTEROIDS: IMPACT ON COLLABORATION The International Workshop June 15–18, 2003 Kharkiv, Ukraine A B S T R A C T S The Organizing Committee: Lupishko Dmitrij (co-Chairman), Kiselev Nikolai (co-Chairman), Belskaya Irina, Krugly Yurij, Shevchenko Vasilij, Velichko Fiodor, Luk’yanyk Igor Kharkiv - 2003 2 Contents Belskaya I.N., Shevchenko V.G., Efimov Yu.S., Shakhovskoj N.M., Gaftonyuk N.M., Krugly Yu.N., Chiorny V.G. Opposition Polarimetry and Photometry of Asteroids 5 Bochkov V.V., Prokof’eva V.V. Spectrophotometric Observations of Asteroids in the Crimean Astrophysical Observatory 6 Butenko G., Gerashchenko O., Ivashchenko Yu., Kazantsev A., Koval’chuk G., Lokot V. Estimates of Rotation Periods of Asteroids Derived from CCD- Observations in Andrushivka Astronomical Observatory 7 Bykov O.P., L'vov V.N. Method of accuracy estimation of asteroid positional CCD observations and results its application with EPOS Software 7 Cellino A., Gil Hutton R., Di Martino M., Tedesco E.F., Bendjoya Ph. Polarimetric Observations of Asteroids with the Torino UBVRI Photopolarimeter 9 Chiorny V.G., Shevchenko V.G., Krugly Yu.N., Velichko F.P., Gaftonyuk N.M.
    [Show full text]
  • Aten-Alinda Orbital Evolution: the Example of Possible Interacting Orbits
    ATEN-ALINDA ORBITAL EVOLUTION: THE EXAMPLE OF POSSIBLE INTERACTING ORBITS A. Rosaev FGUP NPC "NEDRA" Minor planets 887 Alinda and 2062 Aten are typical 1. INTRODUCTION near Earth asteroids (NEA). Our previous researches show their possible origin in catastrophic collision near Minor planets 887 Alinda and 2062 Aten are typical Earth orbit. It is determine the target of present near earth objects ((NEA). They represent different research – to investigate interactions between these dynamical groups of NEA, Amor's and Aten's groups objects in more details. accordingly. The origin of Aten's group has a particular Orbits m.p. 887 and 2062 are crossed near pericenter interest due to specific character of their orbits. The and apocenter accordingly. So possible interval of the elements of orbits m.p. 887 and 2062 are given in the interaction of these objects is repeated through the table 1. significant time interval and has relatively small Orbits m.p. 887 and 2062 are crossed near pericenter duration. and apocenter accordingly (Fig.1). So possible interval On the strength of several reasons, orbits of fragments of the interaction of these objects is repeated through of the disastrous collision can have no an exact the significant time interval and has relatively small intersection. Besides, when integrating on the greater duration. gap in the past increases a role of the uncertainty of Table1 initial values of elements of orbits. These factors Aten – Alinda orbital elements determine a probabilistic nature of the result as well as need of modeling of the disastrous process. However, on the strength of the specific spatial location of orbits, Element Aten Alinda result has highly determined numeric expression - in q 0.79 1.08 the suggestion on the possible interaction m.
    [Show full text]
  • Fast and Slow Rotation of Asteroids
    Icarus 148, 12–20 (2000) doi:10.1006/icar.2000.6482, available online at http://www.idealibrary.com on Fast and Slow Rotation of Asteroids Petr Pravec Astronomical Institute, Academy of Sciences of the Czech Republic, CZ-25165 Ondrejov,ˇ Czech Republic E-mail: [email protected] and Alan W. Harris Jet Propulsion Laboratory, 4800 Oak Grove Drive, Pasadena, California 91109 Received September 27, 1999; revised December 22, 1999 of rotation rates, both fast and slow, which are most anomalous We present an analysis of the distribution of asteroid spin rates vs. among the smallest asteroids. size. The existence of significant populations of both slow and fast rotators among asteroids smaller than D = 40 km, and especially 2. SPIN DATA below 10 km (where our sample is mostly near-Earth asteroids), is shown. We have found that the excess of slow rotators is present We utilized lists of asteroid periods and lightcurve amplitudes at spin rates below 0.8 rev/day, and the group of fast rotators oc- compiled by A. Harris (version 1997 October) and P. Pravec cupies the range of spin rates >7 rev/day. The fast rotators show (NEAs; version 1999 June). The lists are available from the au- interesting characteristics: The lack of objects rotating faster than thors upon request. From the lists, data for near-Earth asteroids, 2.2 h period among asteroids with absolute magnitude H < 22, as Mars-crossers, and main belt asteroids with quality codes Q 2 well as the tendency to spheroidal shapes of fast rotators, is evi- have been selected; see Harris and Young (1983) for a descrip- dence that asteroids larger than a few hundred meters are mostly tion of the quality codes.
    [Show full text]
  • Cumulative Index to Volumes 1-45
    The Minor Planet Bulletin Cumulative Index 1 Table of Contents Tedesco, E. F. “Determination of the Index to Volume 1 (1974) Absolute Magnitude and Phase Index to Volume 1 (1974) ..................... 1 Coefficient of Minor Planet 887 Alinda” Index to Volume 2 (1975) ..................... 1 Chapman, C. R. “The Impossibility of 25-27. Index to Volume 3 (1976) ..................... 1 Observing Asteroid Surfaces” 17. Index to Volume 4 (1977) ..................... 2 Tedesco, E. F. “On the Brightnesses of Index to Volume 5 (1978) ..................... 2 Dunham, D. W. (Letter regarding 1 Ceres Asteroids” 3-9. Index to Volume 6 (1979) ..................... 3 occultation) 35. Index to Volume 7 (1980) ..................... 3 Wallentine, D. and Porter, A. Index to Volume 8 (1981) ..................... 3 Hodgson, R. G. “Useful Work on Minor “Opportunities for Visual Photometry of Index to Volume 9 (1982) ..................... 4 Planets” 1-4. Selected Minor Planets, April - June Index to Volume 10 (1983) ................... 4 1975” 31-33. Index to Volume 11 (1984) ................... 4 Hodgson, R. G. “Implications of Recent Index to Volume 12 (1985) ................... 4 Diameter and Mass Determinations of Welch, D., Binzel, R., and Patterson, J. Comprehensive Index to Volumes 1-12 5 Ceres” 24-28. “The Rotation Period of 18 Melpomene” Index to Volume 13 (1986) ................... 5 20-21. Hodgson, R. G. “Minor Planet Work for Index to Volume 14 (1987) ................... 5 Smaller Observatories” 30-35. Index to Volume 15 (1988) ................... 6 Index to Volume 3 (1976) Index to Volume 16 (1989) ................... 6 Hodgson, R. G. “Observations of 887 Index to Volume 17 (1990) ................... 6 Alinda” 36-37. Chapman, C. R. “Close Approach Index to Volume 18 (1991) ..................
    [Show full text]
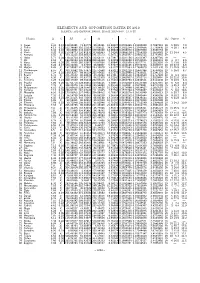
  • 000001 – 004000
    ELEMENTS AND OPPOSITION DATES IN 2019 ecliptic and equinox 2000.0, epoch 2019 nov. 13.0 tt Planet H G M ω Ω i e µ a TE Oppos. V m ◦ ◦ ◦ ◦ ◦ 1 Ceres 3.34 0.12 119.82381 73.83775 80.30381 10.59227 0.0766486 0.21382049 2.7697241 19 5 29.5 7.0 2 Pallas 4.13 0.11 102.34880 310.11514 173.06521 34.83144 0.2302254 0.21343666 2.7730436 19 4 19.7 8.0 3 Juno 5.33 0.32 80.16992 248.10327 169.85020 12.99008 0.2569240 0.22607900 2.6686763 19 — — 4 Vesta 3.20 0.32 150.08773 150.81931 103.80943 7.14181 0.0886118 0.27154209 2.3618081 19 11 14.4 6.5 5 Astraea 6.85 X 330.11215 358.66021 141.57172 5.36711 0.1910347 0.23861125 2.5743965 19 — — 6 Hebe 5.71 0.24 138.43724 239.76676 138.64111 14.73917 0.2031156 0.26103397 2.4247746 19 — — 7 Iris 5.51 X 193.93164 145.25948 259.56318 5.52359 0.2308299 0.26741555 2.3860431 19 4 2.7 9.5 8 Flora 6.49 0.28 255.13638 285.32867 110.87666 5.88846 0.1560358 0.30157711 2.2022695 19 5 13.8 9.8 9 Metis 6.28 0.17 330.40220 6.37267 68.90957 5.57674 0.1232185 0.26742705 2.3859747 19 10 27.6 8.6 10 Hygiea 5.43 X 187.50982 312.37901 283.19878 3.83172 0.1122683 0.17695679 3.1421330 19 11 25.9 10.3 11 Parthenope 6.55 X 330.37882 195.37875 125.52860 4.63112 0.1002229 0.25647388 2.4534316 19 5 16.0 9.7 12 Victoria 7.24 0.22 188.58207 69.66124 235.40635 8.37272 0.2202999 0.27638851 2.3341175 19 — — 13 Egeria 6.74 X 235.23502 80.49624 43.21994 16.53617 0.0852529 0.23841640 2.5757990 19 9 8.1 10.8 14 Irene 6.30 X 212.36883 97.83775 86.12300 9.12162 0.1663937 0.23700714 2.5859994 19 10 21.0 10.6 15 Eunomia 5.28 0.23 329.17049 98.58234
    [Show full text]
  • Detection of Semimajor Axis Drifts in 54 Near-Earth Asteroids: New Measurements of the Yarkovsky Effect
    The Astronomical Journal, 144:60 (13pp), 2012 August doi:10.1088/0004-6256/144/2/60 C 2012. The American Astronomical Society. All rights reserved. Printed in the U.S.A. DETECTION OF SEMIMAJOR AXIS DRIFTS IN 54 NEAR-EARTH ASTEROIDS: NEW MEASUREMENTS OF THE YARKOVSKY EFFECT C. R. Nugent1, J. L. Margot1,2,S.R.Chesley3, and D. Vokrouhlicky´ 4 1 Department of Earth and Space Sciences, University of California, Los Angeles, CA 90095, USA 2 Department of Physics and Astronomy, University of California, Los Angeles, CA 90095, USA 3 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA 4 Institute of Astronomy, Charles University, V Holesovi˘ ck˘ ach´ 2, CZ-18000 Prague 8, Czech Republic Received 2012 April 16; accepted 2012 June 7; published 2012 July 12 ABSTRACT We have identified and quantified semimajor axis drifts in near-Earth asteroids (NEAs) by performing orbital fits to optical and radar astrometry of all numbered NEAs. We focus on a subset of 54 NEAs that exhibit some of the most reliable and strongest drift rates. Our selection criteria include a Yarkovsky sensitivity metric that quantifies the detectability of semimajor axis drift in any given data set, a signal-to-noise metric, and orbital coverage requirements. In 42 cases, the observed drifts (∼10−3 AU Myr−1) agree well with numerical estimates of Yarkovsky drifts. This agreement suggests that the Yarkovsky effect is the dominant non-gravitational process affecting these orbits, and allows us to derive constraints on asteroid physical properties. In 12 cases, the drifts exceed nominal Yarkovsky predictions, which could be due to inaccuracies in our knowledge of physical properties, faulty astrometry, or modeling errors.
    [Show full text]
  • Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect
    University of California Los Angeles Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Geophysics and Space Physics by Carolyn Rosemary Nugent 2013 c Copyright by Carolyn Rosemary Nugent 2013 Abstract of the Dissertation Solar Radiation and Near-Earth Asteroids: Thermophysical Modeling and New Measurements of the Yarkovsky Effect by Carolyn Rosemary Nugent Doctor of Philosophy in Geophysics and Space Physics University of California, Los Angeles, 2013 Professor Jean-Luc Margot, Chair This dissertation examines the influence of solar radiation on near-Earth asteroids (NEAs); it investigates thermal properties and examines changes to orbits caused by the process of anisotropic re-radiation of sunlight called the Yarkovsky effect. For the first portion of this dissertation, we used geometric albedos (pV ) and diameters derived from the Wide-Field Infrared Survey Explorer (WISE), as well as geometric albedos and diameters from the literature, to produce more accurate diurnal Yarkovsky drift predic- tions for 540 NEAs out of the current sample of ∼ 8800 known objects. These predictions are intended to assist observers, and should enable future Yarkovsky detections. The second portion of this dissertation introduces a new method for detecting the Yarkovsky drift. We identified and quantified semi-major axis drifts in NEAs by performing orbital fits to optical and radar astrometry of all numbered NEAs. We discuss on a subset of 54 NEAs that exhibit some of the most reliable and strongest drift rates. Our selection criteria include a Yarkovsky sensitivity metric that quantifies the detectability of semi-major axis drift in any given data set, a signal-to-noise metric, and orbital coverage requirements.
    [Show full text]
  • The Minor Planet Bulletin Reporting the Present Publication
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 42, NUMBER 1, A.D. 2015 JANUARY-MARCH 1. NIR MINOR PLANET PHOTOMETRY FROM BURLEITH 359 Georgia. The observed rotation is in close agreement with OBSERVATORY: 2014 FEBRUARY – JUNE Lagerkvist (1978). Richard E. Schmidt 462 Eriphyla. The observing sessions of duration 3.5 hours on Burleith Observatory (I13) 2014 Feb 22 and 3.3 hours on 2014 March 16 appear to indicate 1810 35th St NW that the true rotation period is twice that found by Behrend (2006). Washington, DC 20007 [email protected] 595 Polyxena. The observed rotation is in close agreement with Piironen et al. (1998). (Received: 19 August Revised: 5 September) 616 Elly. Alvarez-Candal et al.(2004) found a period of 5.301 h. Rotation periods were obtained for ten minor planets 782 Montefiore. These observations confirm the period of based on near-IR CCD observations made in 2014 at the Wisniewski et al. (1997). urban Burleith Observatory, Washington, DC. 953 Painleva. At Mv = 14 and amplitude 0.05 mag, a low confidence in these results should be assumed. Ditteon and In the city of Washington, DC, increasing light pollution brought Hawkins (2007) found no period over two nights. on by the installation of “decorative” street lights has severely limited opportunities for minor planet photometry. In 2014 a test 1019 Strackea. A member of the high-inclination (i = 27°) selection of bright minor planets of both high and low amplitude Hungaria group, Strackea has been an object of much interest of were chosen to study the feasibility of differential photometry in late.
    [Show full text]