DOCSLIB.ORG

Statistical Methods for Practitioners (EPA QA/G-9S)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistical Methods for Practitioners (EPA QA/G-9S) United States Office of Environmental Environmental Protection Information EPA/240/B-06/003 Agency Washington, DC 20460 February 2006 Data Quality Assessment: Statistical Methods for Practitioners EPA QA/G-9S FOREWORD This document, Data Quality Assessment: Statistical Methods for Practitioners, provides general guidance to organizations on assessing data quality criteria and performance specifications. The Environmental Protection Agency (EPA) has developed the Data Quality Assessment (DQA) Process for project managers and planners to determine whether the type, quantity, and quality of data needed to support Agency decision making has been achieved. This guidance is the culmination of experiences in the design and statistical analyses of environmental data in different Program Offices at the EPA. Many elements of prior guidance, statistics, and scientific planning have been incorporated into this document. This document is one of a series of quality management guidance documents that the EPA Quality Staff has prepared to assist users in implementing the Agency-wide Quality System. Other related documents include: EPA QA/G-4 Guidance on Systematic Planning Using the Data Quality Objectives Process EPA QA/G-5S Guidance on Choosing a Sampling Design for Environmental Data Collection EPA QA/G-9R Data Quality Assessment: A Reviewer’s Guide This document provides guidance to EPA program managers and planning teams as well as to the general public as appropriate. It does not impose legally binding requirements and may not apply to a particular situation based on the circumstances. EPA retains the discretion to adopt approaches on a case-by-case basis that differ from this guidance where appropriate. This guidance is one of the U.S Environmental Protection Agency Quality System Series documents. These documents describe the EPA policies and procedures for planning, implementing, and assessing the effectiveness of the Quality System. These documents are updated periodically to incorporate new topics and revision or refinements to existing procedures. Comments received on this, the 2006 version, will be considered for inclusion in subsequent versions. Please send your comments to: Quality Staff (2811R) U.S. Environmental Protection Agency 1200 Pennsylvania Avenue, NW Washington, DC 20460 Phone: (202) 564-6830 Fax: (202) 565-2441 E-mail: [email protected] Copies of the EPA Quality System documents may be downloaded from the Quality Staff Home Page: www.epa.gov.quality. EPA QA/G-9S iii February 2006 PREFACE Data Quality Assessment: Statistical Methods for Practitioners describes the statistical methods used in Data Quality Assessment (DQA) in evaluating environmental data sets. DQA is the scientific and statistical evaluation of environmental data to determine if they meet the planning objectives of the project, and thus are of the right type, quality, and quantity to support their intended use. This guidance applies DQA to environmental decision-making (e.g., compliance determinations) and also addresses DQA in environmental estimation (e.g., monitoring programs). This document is distinctly different from other guidance documents in that it is not intended to be read in a linear or continuous fashion. Instead, it is intended to be used as a "tool-box" of useful techniques in assessing the quality of data. The overall structure of the document will enable the analyst to investigate many problems using a systematic methodology. Each statistical technique examined in the text is demonstrated separately in the form of a series of steps to be taken. The technique is then illustrated with a practical example following the steps described. This document is intended for all EPA and extramural organizations that have quality systems based on EPA policies and specifications, and that may periodically assess these quality systems (or have them assessed by EPA) for compliance to the specifications. In addition, this guidance may be used by other organizations that assess quality systems applied to specific environmental programs. The guidance provided herein is non-mandatory and is intended to help personnel who have minimal experience with statistical terminology to understand how a technique works and how it may be applied to a problem. An explanation of DQA in plain English may be found in the companion guidance document, Data Quality Assessment: A Reviewer’s Guide (EPA QA/G-9R) (U.S. EPA, 2006b). EPA QA/G-9S iv February 2006 TABLE OF CONTENTS Page INTRODUCTION......................................................................................................................... 1 STEP 1: REVIEW DQOs AND THE SAMPLING DESIGN.................................................. 5 1.1 OVERVIEW AND ACTIVITIES............................................................................6 STEP 2: CONDUCT A PRELIMINARY DATA REVIEW.................................................... 9 2.1 OVERVIEW AND ACTIVITIES..........................................................................12 2.2 STATISTICAL QUANTITIES.............................................................................12 2.2.1 Measures of Relative Standing ..................................................................12 2.2.2 Measures of Central Tendency ..................................................................13 2.2.3 Measures of Dispersion..............................................................................15 2.2.4 Measures of Association............................................................................16 2.2.4.1 Pearson’s Correlation Coefficient................................................16 2.2.4.2 Spearman’s Rank Correlation......................................................18 2.2.4.3 Serial Correlation.........................................................................18 2.3 GRAPHICAL REPRESENTATIONS...................................................................20 2.3.1 Histogram...................................................................................................20 2.3.2 Stem-and-Leaf Plot....................................................................................21 2.3.3 Box-and-Whiskers Plot..............................................................................23 2.3.4 Quantile Plot and Ranked Data Plots.........................................................25 2.3.5 Quantile-Quantile Plots and Probability Plots ...........................................26 2.3.6 Plots for Two or More Variables ...............................................................27 2.3.6.1 Scatterplot ....................................................................................29 2.3.6.2 Extensions of the Scatterplot .......................................................30 2.3.6.3 Empirical Quantile-Quantile Plot ................................................31 2.3.7 Plots for Temporal Data.............................................................................32 2.3.7.1 Time Plot......................................................................................33 2.3.7.2 Lag Plot........................................................................................34 2.3.7.3 Plot of the Autocorrelation Function (Correlogram) ...................34 2.3.7.4 Multiple Observations in a Time Period......................................35 2.3.7.5 Four-Plot ......................................................................................36 2.3.8 Plots for Spatial Data .................................................................................37 2.3.8.1 Posting Plots................................................................................38 2.3.8.2 Symbol Plots and Bubble Plots....................................................39 2.3.8.3 Other Spatial Graphical Representations.....................................39 2.4 PROBABILITY DISTRIBUTIONS......................................................................40 2.4.1 The Normal Distribution............................................................................40 2.4.2 The t-Distribution.......................................................................................41 2.4.3 The Lognormal Distribution ......................................................................41 2.4.4 Central Limit Theorem ..............................................................................41 STEP 3: SELECT THE STATISTICAL METHOD.............................................................. 43 3.1 OVERVIEW AND ACTIVITIES..........................................................................46 3.2 METHODS FOR A SINGLE POPULATION ......................................................46 3.2.1 Parametric Methods...................................................................................48 3.2.1.1 The One-Sample t-test and Confidence Interval or Limit ...........48 EPA QA/G-9S v February 2006 Page 3.2.1.2 The One-Sample Tolerance Interval or Limit..............................48 3.2.1.3 Stratified Random Sampling........................................................51 3.2.1.4 The Chen Test..............................................................................52 3.2.1.5 Land’s Method for Lognormally Distributed Data......................57 3.2.1.6 The One-Sample Proportion Test and Confidence Interval.........58 3.2.2 Nonparametric Methods.............................................................................60 3.2.2.1 The Sign Test ...............................................................................60 3.2.2.2
Load more

Recommended publications
  • Appendix a Basic Statistical Concepts for Sensory Evaluation
    Appendix A Basic Statistical Concepts for Sensory Evaluation Contents This chapter provides a quick introduction to statistics used for sensory evaluation data including measures of A.1 Introduction ................ 473 central tendency and dispersion. The logic of statisti- A.2 Basic Statistical Concepts .......... 474 cal hypothesis testing is introduced. Simple tests on A.2.1 Data Description ........... 475 pairs of means (the t-tests) are described with worked A.2.2 Population Statistics ......... 476 examples. The meaning of a p-value is reviewed. A.3 Hypothesis Testing and Statistical Inference .................. 478 A.3.1 The Confidence Interval ........ 478 A.3.2 Hypothesis Testing .......... 478 A.3.3 A Worked Example .......... 479 A.1 Introduction A.3.4 A Few More Important Concepts .... 480 A.3.5 Decision Errors ............ 482 A.4 Variations of the t-Test ............ 482 The main body of this book has been concerned with A.4.1 The Sensitivity of the Dependent t-Test for using good sensory test methods that can generate Sensory Data ............. 484 quality data in well-designed and well-executed stud- A.5 Summary: Statistical Hypothesis Testing ... 485 A.6 Postscript: What p-Values Signify and What ies. Now we turn to summarize the applications of They Do Not ................ 485 statistics to sensory data analysis. Although statistics A.7 Statistical Glossary ............. 486 are a necessary part of sensory research, the sensory References .................... 487 scientist would do well to keep in mind O’Mahony’s admonishment: statistical analysis, no matter how clever, cannot be used to save a poor experiment. The techniques of statistical analysis, do however, It is important when taking a sample or designing an serve several useful purposes, mainly in the efficient experiment to remember that no matter how powerful summarization of data and in allowing the sensory the statistics used, the inferences made from a sample scientist to make reasonable conclusions from the are only as good as the data in that sample.
    [Show full text]
  • Statistical Characterization of Tissue Images for Detec- Tion and Classification of Cervical Precancers
    Statistical characterization of tissue images for detec- tion and classification of cervical precancers Jaidip Jagtap1, Nishigandha Patil2, Chayanika Kala3, Kiran Pandey3, Asha Agarwal3 and Asima Pradhan1, 2* 1Department of Physics, IIT Kanpur, U.P 208016 2Centre for Laser Technology, IIT Kanpur, U.P 208016 3G.S.V.M. Medical College, Kanpur, U.P. 208016 * Corresponding author: [email protected], Phone: +91 512 259 7971, Fax: +91-512-259 0914. Abstract Microscopic images from the biopsy samples of cervical cancer, the current “gold standard” for histopathology analysis, are found to be segregated into differing classes in their correlation properties. Correlation domains clearly indicate increasing cellular clustering in different grades of pre-cancer as compared to their normal counterparts. This trend manifests in the probabilities of pixel value distribution of the corresponding tissue images. Gradual changes in epithelium cell density are reflected well through the physically realizable extinction coefficients. Robust statistical parameters in the form of moments, characterizing these distributions are shown to unambiguously distinguish tissue types. These parameters can effectively improve the diagnosis and classify quantitatively normal and the precancerous tissue sections with a very high degree of sensitivity and specificity. Key words: Cervical cancer; dysplasia, skewness; kurtosis; entropy, extinction coefficient,. 1. Introduction Cancer is a leading cause of death worldwide, with cervical cancer being the fifth most common cancer in women [1-2]. It originates as a few abnormal cells in the initial stage and then spreads rapidly. Treatment of cancer is often ineffective in the later stages, which makes early detection the key to survival. Pre-cancerous cells can sometimes take 10-15 years to develop into cancer and regular tests such as pap-smear are recommended.
    [Show full text]
  • An Overview of Environmental Statistics
    An Overview of Environmental Statistics Richard L. Smith Department of Statistics and Operations Research University of North Carolina Chapel Hill, N.C., U.S.A. Theme Day in Environmental Statistics 55th Session of ISI Sydney, April 6, 2005 http://www.stat.unc.edu/postscript/rs/isitutorial.pdf 1 Environmental Statistics is by now an extremely broad field, in- volving application of just about every technique of statistics. Examples: • Pollution in atmosphere and water systems • Effects of pollution on human health and ecosystems • Uncertainties in forecasting climate and weather • Dynamics of ecological time series • Environmental effects on the genome and many more. 2 Some common themes: • Most problems involve time series of observations, but also spatial sampling, often involving irregular grids • Design of a spatial sampling scheme or a monitor network is important • Often the greatest interest is in extremes, for example – Air pollution standards often defined by number of cross- ings of a high threshold – Concern over impacts of climate change often focussed on climate extremes. Hence, must be able to character- ize likely frequencies of extreme events in future climate scenarios • Use of numerical models — not viewed in competition, but how we can use statistics to improve the information derived from models 3 I have chosen here to focus on three topics that have applications across several of these areas: I. Spatial and spatio-temporal statistics • Interpolation of an air pollution or meteorological field • Comparing data measured on different spatial scales • Assessing time trends in data collected on a spatial net- work II. Network design • Choosing where to place the monitors to satisfy some optimality criterion related to prediction or estimation III.
    [Show full text]
  • Case Study Applications of Statistics in Institutional Research
    /-- ; / \ \ CASE STUDY APPLICATIONS OF STATISTICS IN INSTITUTIONAL RESEARCH By MARY ANN COUGHLIN and MARIAN PAGAN( Case Study Applications of Statistics in Institutional Research by Mary Ann Coughlin and Marian Pagano Number Ten Resources in Institutional Research A JOINTPUBLICA TION OF THE ASSOCIATION FOR INSTITUTIONAL RESEARCH AND THE NORTHEASTASSO CIATION FOR INSTITUTIONAL REASEARCH © 1997 Association for Institutional Research 114 Stone Building Florida State University Ta llahassee, Florida 32306-3038 All Rights Reserved No portion of this book may be reproduced by any process, stored in a retrieval system, or transmitted in any form, or by any means, without the express written permission of the publisher. Printed in the United States To order additional copies, contact: AIR 114 Stone Building Florida State University Tallahassee FL 32306-3038 Tel: 904/644-4470 Fax: 904/644-8824 E-Mail: [email protected] Home Page: www.fsu.edul-airlhome.htm ISBN 1-882393-06-6 Table of Contents Acknowledgments •••••••••••••••••.•••••••••.....••••••••••••••••.••. Introduction .•••••••••••..•.•••••...•••••••.....••••.•••...••••••••• 1 Chapter 1: Basic Concepts ..•••••••...••••••...••••••••..••••••....... 3 Characteristics of Variables and Levels of Measurement ...................3 Descriptive Statistics ...............................................8 Probability, Sampling Theory and the Normal Distribution ................ 16 Chapter 2: Comparing Group Means: Are There Real Differences Between Av erage Faculty Salaries Across Departments? •...••••••••.••.••••••
    [Show full text]
  • The Instat Guide to Choosing and Interpreting Statistical Tests
    Statistics for biologists The InStat Guide to Choosing and Interpreting Statistical Tests GraphPad InStat Version 3 for Macintosh By GraphPad Software, Inc. © 1990-2001,,, GraphPad Soffftttware,,, IIInc... Allllll riiighttts reserved... Program design, manual and help Dr. Harvey J. Motulsky screens: Paige Searle Programming: Mike Platt John Pilkington Harvey Motulsky Maciiintttosh conversiiion by Soffftttware MacKiiiev... www...mackiiiev...com Project Manager: Dennis Radushev Programmers: Alexander Bezkorovainy Dmitry Farina Quality Assurance: Lena Filimonihina Help and Manual: Pavel Noga Andrew Yeremenko InStat and GraphPad Prism are registered trademarks of GraphPad Software, Inc. All Rights Reserved. Manufactured in the United States of America. Except as permitted under the United States copyright law of 1976, no part of this publication may be reproduced or distributed in any form or by any means without the prior written permission of the publisher. Use of the software is subject to the restrictions contained in the accompanying software license agreement. How ttto reach GraphPad: Phone: (US) 858-457-3909 Fax: (US) 858-457-8141 Email: [email protected] or [email protected] Web: www.graphpad.com Mail: GraphPad Software, Inc. 5755 Oberlin Drive #110 San Diego, CA 92121 USA The entire text of this manual is available on-line at www.graphpad.com Contents Welcome to InStat........................................................................................7 The InStat approach ---------------------------------------------------------------7
    [Show full text]
  • One Sample T Test
    Copyright c October 17, 2020 by NEH One Sample t Test Nathaniel E. Helwig University of Minnesota 1 How Beer Changed the World William Sealy Gosset was a chemist and statistician who was employed as the Head Exper- imental Brewer at Guinness in the early 1900s. As a part of his job, Gosset was responsible for taking samples of beer and performing various analyses to ensure that the beer was of the proper composition and quality. While at Guinness, Gosset taught himself experimental design and statistical analysis (which were new and exciting fields at the time), and he even spent some time in 1906{1907 studying in Karl Pearson's laboratory. Gosset's work often involved collecting a small number of samples, and testing hypotheses about the mean of the population from which the samples were drawn. For example, in the brewery, Gosset may want to test whether the population mean amount of some ingredient (e.g., barley) was equal to the intended value. And, on the farm, Gosset may want to test how different farming techniques and growing conditions affect the barley yields. Through this work, Gos- set noticed that the normal distribution was not adequate for testing hypotheses about the mean in small samples of data with an unknown variance. 2 2 1 Pn As a reminder, if X ∼ N(µ, σ ), thenx ¯ ∼ N(µ, σ =n) wherex ¯ = n i=1 xi, which implies x¯ − µ Z = p ∼ N(0; 1) σ= n i.e., the Z test statistic follows a standard normal distribution. However, in practice, the 2 2 1 Pn 2 population variance σ is often unknown, so the sample variance s = n−1 i=1(xi − x¯) must be used in its place.
    [Show full text]
  • Data Analysis Considerations in Producing 'Comparable' Information
    Data Analysis Considerations in Producing ‘Comparable’ Information for Water Quality Management Purposes Lindsay Martin Griffith, Assistant Engineer, Brown and Caldwell Robert C. Ward, Professor, Colorado State University Graham B. McBride, Principal Scientist, NIWA (National Institute of Water and Atmospheric Research), Hamilton, New Zealand Jim C. Loftis, Professor, Colorado State University A report based on thesis material prepared by the lead author as part of the requirement for the degree of Master of Science from Colorado State University February 2001 ABSTRACT Water quality monitoring is being used in local, regional, and national scales to measure how water quality variables behave in the natural environment. A common problem, which arises from monitoring, is how to relate information contained in data to the information needed by water resource management for decision-making. This is generally attempted through statistical analysis of the monitoring data. However, how the selection of methods with which to routinely analyze the data affects the quality and comparability of information produced is not as well understood as may first appear. To help understand the connectivity between the selection of methods for routine data analysis and the information produced to support management, the following three tasks were performed. S An examination of the methods that are currently being used to analyze water quality monitoring data, including published criticisms of them. S An exploration of how the selection of methods to analyze water quality data can impact the comparability of information used for water quality management purposes. S Development of options by which data analysis methods employed in water quality management can be made more transparent and auditable.
    [Show full text]
  • Estimating Suitable Probability Distribution Function for Multimodal Traffic Distribution Function
    Journal of the Korean Society of Marine Environment & Safety Research Paper Vol. 21, No. 3, pp. 253-258, June 30, 2015, ISSN 1229-3431(Print) / ISSN 2287-3341(Online) http://dx.doi.org/10.7837/kosomes.2015.21.3.253 Estimating Suitable Probability Distribution Function for Multimodal Traffic Distribution Function Sang-Lok Yoo* ․ Jae-Yong Jeong** ․ Jeong-Bin Yim** * Graduate school of Mokpo National Maritime University, Mokpo 530-729, Korea ** Professor, Mokpo National Maritime University, Mokpo 530-729, Korea Abstract : The purpose of this study is to find suitable probability distribution function of complex distribution data like multimodal. Normal distribution is broadly used to assume probability distribution function. However, complex distribution data like multimodal are very hard to be estimated by using normal distribution function only, and there might be errors when other distribution functions including normal distribution function are used. In this study, we experimented to find fit probability distribution function in multimodal area, by using AIS(Automatic Identification System) observation data gathered in Mokpo port for a year of 2013. By using chi-squared statistic, gaussian mixture model(GMM) is the fittest model rather than other distribution functions, such as extreme value, generalized extreme value, logistic, and normal distribution. GMM was found to the fit model regard to multimodal data of maritime traffic flow distribution. Probability density function for collision probability and traffic flow distribution will be calculated much precisely in the future. Key Words : Probability distribution function, Multimodal, Gaussian mixture model, Normal distribution, Maritime traffic flow 1. Introduction* traffic time and speed. Some studies estimated the collision probability when the ship Maritime traffic flow is affected by the volume of traffic, tidal is in confronting or passing by applying it to normal distribution current, wave height, and so on.
    [Show full text]
  • Regression Assumptions in Clinical Psychology Research Practice—A Systematic Review of Common Misconceptions
    Regression assumptions in clinical psychology research practice—a systematic review of common misconceptions Anja F. Ernst and Casper J. Albers Heymans Institute for Psychological Research, University of Groningen, Groningen, The Netherlands ABSTRACT Misconceptions about the assumptions behind the standard linear regression model are widespread and dangerous. These lead to using linear regression when inappropriate, and to employing alternative procedures with less statistical power when unnecessary. Our systematic literature review investigated employment and reporting of assumption checks in twelve clinical psychology journals. Findings indicate that normality of the variables themselves, rather than of the errors, was wrongfully held for a necessary assumption in 4% of papers that use regression. Furthermore, 92% of all papers using linear regression were unclear about their assumption checks, violating APA- recommendations. This paper appeals for a heightened awareness for and increased transparency in the reporting of statistical assumption checking. Subjects Psychiatry and Psychology, Statistics Keywords Linear regression, Statistical assumptions, Literature review, Misconceptions about normality INTRODUCTION One of the most frequently employed models to express the influence of several predictors Submitted 18 November 2016 on a continuous outcome variable is the linear regression model: Accepted 17 April 2017 Published 16 May 2017 Yi D β0 Cβ1X1i Cβ2X2i C···CβpXpi C"i: Corresponding author Casper J. Albers, [email protected] This equation predicts the value of a case Yi with values Xji on the independent variables Academic editor Xj (j D 1;:::;p). The standard regression model takes Xj to be measured without error Shane Mueller (cf. Montgomery, Peck & Vining, 2012, p. 71). The various βj slopes are each a measure of Additional Information and association between the respective independent variable Xj and the dependent variable Y.
    [Show full text]
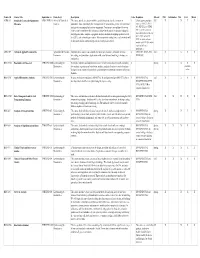
  • The Complete List of Courses, Including Course Descriptions, Prerequisites
    Course ID Course Title Equivalent to Home Dept. Description Units Requisites Offered PhD Informatics MS Cert. Minor ACBS 513 Statistical Genetics for Quantitative ANS/GENE 513 Animal & Biomedical This course provide the student with the statistical tools to describe variation in 3 A basic genetic principles Fall X X X X Measures Sciences quantitative traits, particularly the decomposition of variation into genetic, environmental, course as ANS 213, GENE and gene by environment interaction components. Convariance (resemblance) between 433, GENE 533, or GENE relatives and heritability will be discussed, along with the topics of epistasis, oligogenic 545. A current course on and polygenic traits, complex segregation analysis, methods of mapping quantitative trait basic statistical principles as GENE 509C or MATH loci (QTL), and estimation procedures. Microarrays have multiple uses, each of which will 509C. A course in linear be discussed and the corresponding statistical analyses described. models as MATH 561 and in statistical inference mathematics. AREC 559 Advanced Applied Econometrics Agricultural & Resource Emphasis in the course is on econometric model specification, estimation, inference, 4 AREC 517, ECON 518, Fall X X X X Economics forecasting, and simulation. Applications with actual data and modeling techniques are ECON 549 emphasized. BIOS 576B Biostatistics for Research CPH/EPID 576B Epidemiology & Descriptive statistics and statistical inference relevant to biomedical research, including 3SpringXXX X Biostatistics data analysis, regression and correlation analysis, analysis of variance, survival analysis, available biological assay, statistical methods for epidemiology and statistical evaluation of clinical online literature. BIOS 576C Applied Biostatistics Analysis CPH/EPID 576C Epidemiology & Integrate methods in biostatistics (EPID 576A, B) and Epidemiology (EPID 573A, B) to 3 BIOS/EPID 576A, Fall X X X X Biostatistics develop analytical skills in an epidemiological project setting.
    [Show full text]
  • Continuous Dependent Variable Models
    Chapter 4 Continuous Dependent Variable Models CHAPTER 4; SECTION A: ANALYSIS OF VARIANCE Purpose of Analysis of Variance: Analysis of Variance is used to analyze the effects of one or more independent variables (factors) on the dependent variable. The dependent variable must be quantitative (continuous). The dependent variable(s) may be either quantitative or qualitative. Unlike regression analysis no assumptions are made about the relation between the independent variable and the dependent variable(s). The theory behind ANOVA is that a change in the magnitude (factor level) of one or more of the independent variables or combination of independent variables (interactions) will influence the magnitude of the response, or dependent variable, and is indicative of differences in parent populations from which the samples were drawn. Analysis is Variance is the basic analytical procedure used in the broad field of experimental designs, and can be used to test the difference in population means under a wide variety of experimental settings—ranging from fairly simple to extremely complex experiments. Thus, it is important to understand that the selection of an appropriate experimental design is the first step in an Analysis of Variance. The following section discusses some of the fundamental differences in basic experimental designs—with the intent merely to introduce the reader to some of the basic considerations and concepts involved with experimental designs. The references section points to some more detailed texts and references on the subject, and should be consulted for detailed treatment on both basic and advanced experimental designs. Examples: An analyst or engineer might be interested to assess the effect of: 1.
    [Show full text]
  • Fitting Population Models to Multiple Sources of Observed Data Author(S): Gary C
    Fitting Population Models to Multiple Sources of Observed Data Author(s): Gary C. White and Bruce C. Lubow Reviewed work(s): Source: The Journal of Wildlife Management, Vol. 66, No. 2 (Apr., 2002), pp. 300-309 Published by: Allen Press Stable URL: http://www.jstor.org/stable/3803162 . Accessed: 07/05/2012 19:10 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Allen Press is collaborating with JSTOR to digitize, preserve and extend access to The Journal of Wildlife Management. http://www.jstor.org FITTINGPOPULATION MODELS TO MULTIPLESOURCES OF OBSERVEDDATA GARYC. WHITE,'Department of Fisheryand WildlifeBiology, Colorado State University,Fort Collins, CO 80523, USA BRUCEC. LUBOW,Colorado Cooperative Fish and WildlifeUnit, Colorado State University,Fort Collins, CO 80523, USA Abstract:The use of populationmodels based on severalsources of data to set harvestlevels is a standardproce- dure most westernstates use for managementof mule deer (Odocoileushemionus), elk (Cervuselaphus), and other game populations.We present a model-fittingprocedure to estimatemodel parametersfrom multiplesources of observeddata using weighted least squares and model selectionbased on Akaike'sInformation Criterion. The pro- cedure is relativelysimple to implementwith modernspreadsheet software. We illustratesuch an implementation using an examplemule deer population.Typical data requiredinclude age and sex ratios,antlered and antlerless harvest,and populationsize.
    [Show full text]