An Elementary Treatise on Conic Sections
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Spherical Curves with Modified Orthogonal Frame 1 Introduction 2
ISSN: 1304-7981 Number: 10, Year:2016, Pages: 60-68 http://jnrs.gop.edu.tr Received: 18.05.2016 Editors-in-Chief : Bilge Hilal C»ad³rc³ Accepted: 06.06.2016 Area Editor: Serkan Demiriz Spherical Curves with Modi¯ed Orthogonal Frame Bahaddin BUKCUa;1 ([email protected]) Murat Kemal KARACANb ([email protected]) aGazi Osman Pasa University, Faculty of Sciences and Arts, Department of Mathematics,60250,Tokat-TURKEY bUsak University, Faculty of Sciences and Arts, Department of Mathematics,1 Eylul Campus, 64200,Usak-TURKEY Abstract - In [2-4,8-9], the authors have characterized the spherical curves in di®erent spaces.In this paper, we shall charac- Keywords - Spherical curves, terize the spherical curves according to modi¯ed orthogonal frame Modi¯ed orthogonal frame in Euclidean 3-space. 1 Introduction In the Euclidean space E3 a spherical unit speed curves and their characterizations are given in [8,9]. In [2-4,7], the authors have characterized the Lorentzian and Dual 3 spherical curves in the Minkowski 3-space E1 . In this paper, we shall characterize the spherical curves according to modi¯ed orthogonal frame in the Euclidean 3-space. 2 Preliminaries We ¯rst recall the classical fundamental theorem of space curves, i.e., curves in Euclid- ean 3-space E3. Let ®(s) be a curve of class C3, where s is the arc-length parameter. Moreover we assume that its curvature ·(s) does not vanish anywhere. Then there exists an orthonormal frame ft; n; bg which satis¯es the Frenet-Serret equation 2 3 2 3 2 3 t0(s) 0 · 0 t(s) 4 n0(s) 5 = 4 ¡· 0 ¿ 5 4 n(s) 5 (1) b0(s) 0 ¡¿ 0 b(s) 1Corresponding Author Journal of New Results in Science 6 (2016) 60-68 61 where t; n and b are the tangent, principal normal and binormal unit vectors, respec- tively, and ¿(s) is the torsion. -

290 E. B. STOUFFER [May-June, SOME CANONICAL FORMS AND
290 E. B. STOUFFER [May-June, SOME CANONICAL FORMS AND ASSOCIATED CANONICAL EXPANSIONS IN PROJECTIVE DIFFERENTIAL GEOMETRY* BY E. B. STOUFFER 1. Introduction. A simplification of the methods of ap proach to any branch of mathematics is always very de sirable. This is particularly true in a geometry, where exten sive analytical machinery must be set up before geometric results can be obtained. This paper is a contribution to the simplification of Wilczynski's methods of attack upon plane and space curves in projective differential geometry.f A canonical form for the fundamental differential equation associated with the curve is determined. It leads at once to a complete and independent system of invariants and co- variants in their canonical form. The determination of the corresponding system in the general form involves only simple substitutions. An associated canonical expansion for the equation or equations of the curve is obtained by very direct methods and the geometrical significance of the corresponding triangle or tetrahedron of reference becomes easily evident. Because of the method of their derivation, the fundamental invariants and covariants obtained are those which have an immediately evident geometrical sig nificance. The methods here employed may be applied to surfaces, both curved and ruled in ordinary space and may also be extended to geometry in hyperspace. The resulting simplifi cations are in some cases quite remarkable. These results will be presented in later papers. * Part of a paper read upon invitation of the Program Committee at a meeting of the Southwestern Section of the Society, St. Louis, November 26, 1927. t See Wilczynski, Projective Differential Geometry of Curves and Ruled Surfaces, Chapters 2, 3 and 13. -

Automated Study of Isoptic Curves: a New Approach with Geogebra∗
Automated study of isoptic curves: a new approach with GeoGebra∗ Thierry Dana-Picard1 and Zoltan Kov´acs2 1 Jerusalem College of Technology, Israel [email protected] 2 Private University College of Education of the Diocese of Linz, Austria [email protected] March 7, 2018 Let C be a plane curve. For a given angle θ such that 0 ≤ θ ≤ 180◦, a θ-isoptic curve of C is the geometric locus of points in the plane through which pass a pair of tangents making an angle of θ.If θ = 90◦, the isoptic curve is called the orthoptic curve of C. For example, the orthoptic curves of conic sections are respectively the directrix of a parabola, the director circle of an ellipse, and the director circle of a hyperbola (in this case, its existence depends on the eccentricity of the hyperbola). Orthoptics and θ-isoptics can be studied for other curves than conics, in particular for closed smooth strictly convex curves,as in [1]. An example of the study of isoptics of a non-convex non-smooth curve, namely the isoptics of an astroid are studied in [2] and of Fermat curves in [3]. The Isoptics of an astroid present special properties: • There exist points through which pass 3 tangents to C, and two of them are perpendicular. • The isoptic curve are actually union of disjoint arcs. In Figure 1, the loops correspond to θ = 120◦ and the arcs connecting them correspond to θ = 60◦. Such a situation has been encountered already for isoptics of hyperbolas. These works combine geometrical experimentation with a Dynamical Geometry System (DGS) GeoGebra and algebraic computations with a Computer Algebra System (CAS). -

HYPERBOLA HYPERBOLA a Conic Is Said to Be a Hyperbola If Its Eccentricity Is Greater Than One
HYPERBOLA HYPERBOLA A Conic is said to be a hyperbola if its eccentricity is greater than one. If S ax22 hxy by 2 2 gx 2 fy c 0 represents a hyperbola then h2 ab 0 and 0 2 2 If S ax2 hxy by 2 gx 2 fy c 0 represents a rectangular hyperbola then h2 ab 0 , 0 and a b 0 x2 y 2 Hyperbola: Equation of the hyperbola in standard form is 1. a2 b2 Hyperbola is symmetric about both the axes. Hyperbola does not passing through the origin and does not meet the Y - axis. Hyperbola curve does not exist between the lines x a and x a . x2 y 2 xx yy x2 y 2 x x y y Notation: S 1 , S1 1 1, S1 1 1, S1 2 1 2 1. a2 b 2 1 a2 b 2 11 a2 b 2 12 a2 b 2 Rectangular hyperbola (or) Equilateral hyperbola : In a hyperbola if the length of the transverse axis (2a) is equal to the length of the conjugate axis (2b) , then the hyperbola is called a rectangular hyperbola or an equilateral hyperbola. The eccentricity of a rectangular hyperbola is 2 . Conjugate hyperbola : The hyperbola whose transverse and conjugate axes are respectively the conjugate and transverse axes of a given hyperbola is called the conjugate hyperbola of the given hyperbola. 2 2 1 x y The equation of the hyperbola conjugate to S 0 is S 1 0 . a2 b 2 If e1 and e2 be the eccentricities of the hyperbola and its conjugate hyperbola then 1 1 2 2 1. -
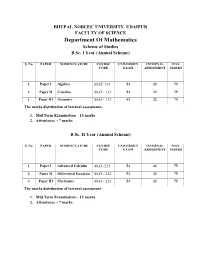
Department of Mathematics Scheme of Studies B.Sc
BHUPAL NOBLES` UNIVERSITY, UDAIPUR FACULTY OF SCIENCE Department Of Mathematics Scheme of Studies B.Sc. I Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Algebra MAT-111 53 22 75 2. Paper II Calculus MAT- 112 53 22 75 3. Paper III Geometry MAT- 113 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. II Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Advanced Calculus MAT-221 53 22 75 2. Paper II Differential Equation MAT- 222 53 22 75 3. Paper III Mechanics MAT- 223 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. III Year (Annual Scheme) S. PAPER NOMENCLATURE COURSE CODE UNIVERSITY INTERNAL MAX. No. EXAM ASSESSMENT MARKS 1. Paper I Real Analysis MAT-331 53 22 75 2. Paper II Advanced Algebra MAT- 332 53 22 75 3. Paper Numerical Analysis MAT-333 (A) 53 22 75 III Mathematical MAT-333 (B) Quantitative Techniques Mathematical MAT-333 (C) Statistics The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks BHUPAL NOBLES’ UNIVERSITY, UDAIPUR Department of Mathematics Syllabus 2017 -2018 (COMMON FOR THE FACULTIES OF ARTS & SCIENCE) B.A. / B. Sc. FIRST YEAR EXAMINATIONS 2017-2020 MATHEMATICS Theory Papers Name Papers Code Papers Maximum Papers hours/ Marks BA/ week B.Sc. Paper I ALGEBRA MAT-111 3 75 Paper II CALCULUS MAT-112 3 75 Paper III GEOMETRY MAT-113 3 75 Total Marks 225 NOTE: 1. -
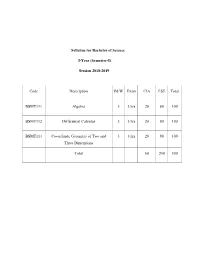
Syllabus for Bachelor of Science I-Year (Semester-I) Session 2018
Syllabus for Bachelor of Science I-Year (Semester-I) Session 2018-2019 Code Description Pd/W Exam CIA ESE Total BSMT111 Algebra 3 3 hrs 20 80 100 BSMT112 Differential Calculus 3 3 hrs 20 80 100 BSMT113 Co-ordinate Geometry of Two and 3 3 hrs 20 80 100 Three Dimensions Total 60 240 300 BSMT111: ALGEBRA Matrix: The characteristic equation of matrix: Eigen Values and Eigen Unit-I Vectors, Diagonalization of matrix, Cayley-Hamilton theorem(Statement 9 and proof),and its use in finding the inverse of a Matrix. Theory of equation: Relation between roots and coefficient of the equation Unit-II Symmetric function of roots. Solution of cubic equation by Cordon’s 9 method and Biquadratic equitation by Ferrari’s method. Infinite series: Convergent series, convergence of geometric series, And Unit-III necessary condition for the convergent series, comparison tests: Cauchy 9 root test. D’Alembert’s Ratio test, Logarithmic test, Raabe’s test, De’ Morgan and Unit-IV Bertrand’s test, Cauchy’s condensation test, Leibnitz’s test of alternative 9 series, Absolute convergent. Unit-V Inequalities and Continued fractions. 9 Suggested Readings: 1. Bhargav and Agarwal:Algebra, Jaipur publishing House, Jaipur. 2. Vashistha and Vashistha : Modern Algebra, Krishna Prakashan, Meerut. 3. Gokhroo, Saini and Tak: Algebra,Navkar prakashan, Ajmer.. 4. M-Ray and H. S. Sharma: A Text book of Higher Algebra, New Delhi, BSMT112: Differential Calculus Unit-I Polar Co-ordinates, Angle between radius vector and the tangents. Angle 9 between curves in polar form, length of polar subs tangent and subnormal, pedal equation of a curve, derivatives of an arc. -

Group B Higher Algebra & Trigonometry
UNIVERSITY DEPARTMENT OF MATHEMATICS, DSPMU, RANCHI CBCS PATTERN SYLLABUS Semester Mat/ Sem VC1- Analytical Geometry 2D, Trigonometry Instruction: Ten questions will be set. Candidates will be required to answer Seven Questions. Question no. 1 will be Compulsory consisting of 10 short answer type covering entire syllabus uniformly. Each question will be of 2 marks. Out of remaining 9 questions candidates will be required to answer 6 questions selecting at least one from each group. Each question will be of 10 marks. GROUP-A ANALYTICAL GEOMETRY OF TWO DIMENSIONS Change of rectangular axes. Condition for the general equation of second degree to represent parabola, ellipse, hyperbola and reduction into standard forms. Equations of tangent and normal (Using Calculus). Chord of contact, Pole and Polar. Pair of tangents in reference to general equation of conic. Axes, centre, director circle in reference to general equation of conic. Polar equation of conic. 5 Questions GROUP B HIGHER ALGEBRA & TRIGONOMETRY Statement and proof of binomial theorem for any index, exponential and logarithmic series. 1 Question De Moivre's theorem and its applications. Trigonometric and Exponential functions of complex argument and hyperbolic functions. Summation of Trigonometrical series. Factorisation of sin , cos 3 Questions Books Recommended: 1. Analytical Geometry& Vector Analysis - B. K. Kar, Books& Allied Co., Kolkata 2. Analytical Geometry of two dimension - Askwith 3. Coordinate Geometry- SL Loney. 4. Trigonometry- Das and Mukheriee 5. Trigonometry- Dasgupta UNIVERSITY DEPARTMENT OF MATHEMATICS, DSPMU, RANCHI CBCS PATTERN SYLLABUS Semester Mat/ Sem IVC 2- Differential Calculus and Vector Calculus Instruction: Ten questions will be set. Candidates will be required to answer Seven Questions. -

1 CHAPTER 2 CONIC SECTIONS 2.1 Introduction a Particle Moving Under the Influence of an Inverse Square Force Moves in an Orbit T
1 CHAPTER 2 CONIC SECTIONS 2.1 Introduction A particle moving under the influence of an inverse square force moves in an orbit that is a conic section; that is to say an ellipse, a parabola or a hyperbola. We shall prove this from dynamical principles in a later chapter. In this chapter we review the geometry of the conic sections. We start off, however, with a brief review (eight equation-packed pages) of the geometry of the straight line. 2.2 The Straight Line It might be thought that there is rather a limited amount that could be written about the geometry of a straight line. We can manage a few equations here, however, (there are 35 in this section on the Straight Line) and shall return for more on the subject in Chapter 4. Most readers will be familiar with the equation y = mx + c 2.2.1 for a straight line. The slope (or gradient) of the line, which is the tangent of the angle that it makes with the x-axis, is m, and the intercept on the y-axis is c. There are various other forms that may be of use, such as x y +=1 2.2.2 x00y yy− 1 yy21− = 2.2.3 xx− 1 xx21− which can also be written x y 1 x1 y1 1 = 0 2.2.4 x2 y2 1 x cos θ + y sin θ = p 2.2.5 2 The four forms are illustrated in figure II.1. y y slope = m y 0 c x x x0 2.2.1 2.2.2 y y • (x2 , y2 ) • ( x1 , y1 ) p x α x 2.2.3 or 4 2.2.5 FIGURE II.1 A straight line can also be written in the form Ax + By + C = 0. -

Osculating Curves and Surfaces*
OSCULATING CURVES AND SURFACES* BY PHILIP FRANKLIN 1. Introduction The limit of a sequence of curves, each of which intersects a fixed curve in « +1 distinct points, which close down to a given point in the limit, is a curve having contact of the «th order with the fixed curve at the given point. If we substitute surface for curve in the above statement, the limiting surface need not osculate the fixed surface, no matter what value » has, unless the points satisfy certain conditions. We shall obtain such conditions on the points, our conditions being necessary and sufficient for contact of the first order, and sufficient for contact of higher order. By taking as the sequence of curves parabolas of the «th order, we obtain theorems on the expression of the »th derivative of a function at a point as a single limit. For the surfaces, we take paraboloids of high order, and obtain such expressions for the partial derivatives. In this case, our earlier restriction, or some other, on the way in which the points close down to the limiting point is necessary. In connection with our discussion of osculating curves, we obtain some interesting theorems on osculating conies, or curves of any given type, which follow from a generalization of Rolle's theorem on the derivative to a theorem on the vanishing of certain differential operators. 2. Osculating curves Our first results concerning curves are more or less well known, and are presented chiefly for the sake of completeness and to orient the later results, t We begin with a fixed curve c, whose equation, in some neighbor- hood of the point x —a, \x —a\<Q, may be written y=f(x). -

Book 6 in the Light and Matter Series of Free Introductory Physics Textbooks
Book 6 in the Light and Matter series of free introductory physics textbooks www.lightandmatter.com The Light and Matter series of introductory physics textbooks: 1 Newtonian Physics 2 Conservation Laws 3 Vibrations and Waves 4 Electricity and Magnetism 5 Optics 6 The Modern Revolution in Physics Benjamin Crowell www.lightandmatter.com Fullerton, California www.lightandmatter.com copyright 1998-2003 Benjamin Crowell edition 3.0 rev. May 15, 2007 This book is licensed under the Creative Com- mons Attribution-ShareAlike license, version 1.0, http://creativecommons.org/licenses/by-sa/1.0/, except for those photographs and drawings of which I am not the author, as listed in the photo credits. If you agree to the license, it grants you certain privileges that you would not otherwise have, such as the right to copy the book, or download the digital version free of charge from www.lightandmatter.com. At your option, you may also copy this book under the GNU Free Documentation License version 1.2, http://www.gnu.org/licenses/fdl.txt, with no invariant sections, no front-cover texts, and no back-cover texts. ISBN 0-9704670-6-0 To Gretchen. Brief Contents 1 Relativity 13 2 Rules of Randomness 43 3 Light as a Particle 67 4 Matter as a Wave 85 5 The Atom 111 Contents 2 Rules of Randomness 2.1 Randomness Isn’t Random . 45 2.2 Calculating Randomness . 46 Statistical independence, 46.—Addition of probabilities, 47.—Normalization, 48.— Averages, 48. 2.3 Probability Distributions . 50 Average and width of a probability distribution, 51. -

The Frenet–Serret Formulas∗
The Frenet–Serret formulas∗ Attila M´at´e Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet–Serret frame of a space curve 1 2 The Frenet–Serret formulas 3 3 The first three derivatives of r 3 4 Examples and discussion 4 4.1 Thecurvatureofacircle ........................... ........ 4 4.2 Thecurvatureandthetorsionofahelix . ........... 5 1 The Frenet–Serret frame of a space curve We will consider smooth curves given by a parametric equation in a three-dimensional space. That is, writing bold-face letters of vectors in three dimension, a curve is described as r = F(t), where F′ is continuous in some interval I; here the prime indicates derivative. The length of such a curve between parameter values t I and t I can be described as 0 ∈ 1 ∈ t1 t1 ′ dr (1) σ(t1)= F (t) dt = dt Z | | Z dt t0 t0 where, for a vector u we denote by u its length; here we assume t is fixed and t is variable, so | | 0 1 we only indicated the dependence of the arc length on t1. Clearly, σ is an increasing continuous function, so it has an inverse σ−1; it is customary to write s = σ(t). The equation − def (2) r = F(σ 1(s)) s J = σ(t): t I ∈ { ∈ } is called the re-parametrization of the curve r = F(t) (t I) with respect to arc length. It is clear that J is an interval. To simplify the description, we will∈ always assume that r = F(t) and s = σ(t), ∗Written for the course Mathematics 2201 (Multivariable Calculus) at Brooklyn College of CUNY. -

The Elementary Differential Geometry of Plane Curves CAMBRIDGE UNIVERSITY PRESS
ilmm mnm IINBINQ LIST QECa 1921 Digitized by the Internet Archive in 2007 with funding from Microsoft Corporation http://www.archive.org/details/elennentarydifferOOfowluoft Cambridge Tracts in Mathematics "; and Mathematical Physics General Editors J. G. LEATHEM, Sc.D. G. H. HARDY, M.A., F.R.S. No. 20 The Elementary Differential Geometry of Plane Curves CAMBRIDGE UNIVERSITY PRESS C. F. CLAY, Manager LONDON : FETTER LANE, E.G. 4 NEW YORK : G. P. PUTNAM'S SONS BOMBAY ") CALCUTTA I MACM I LLAN AND CO., Ltd. MADRAS J TORONTO : J. M. DENT AND SONS, Ltd. TOKYO : MARUZEN-KABUSHIKI-KAISHA ALL RIGHTS RESERVED THE <> ELEMENTARY DIFFERENTIAL GEOMETRY OF PLANE CURVES BY R. H. FOWLER, M.A, Fellow of Trinity College, Cambridge CAMBRIDGE AT THE UNIVERSITY PRESS 1920 4 PKEFACE THIS tract is intended to present a precise account of the elementary differential properties of plane curves. The matter contained is in no sense new, but a suitable connected treatment in the English language has not been available. As a result, a number of interesting misconceptions are current in English text books. It is sufficient to mention two somewhat striking examples, (a) According to the ordinary definition of an envelope, as the locus of the limits of points of intersection of neighbouring curves, a curve is not the envelope of its circles of curvature, for neighbouring circles of curvature do not intersect, (b) The definitions of an asymptote—(1) a straight line, the distance from which of a point on limit of the curve tends to zero as the point tends to infinity ; (2) the a tangent to the curve, whose point of contact tends to infinity—are not equivalent.