Cell Mechanics and Mechanobiology
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1. Introduction to Cell Biology Me239 Statistics
1. introduction to cell biology me239 statistics some information about yourself • 41.7% undergrad • average year: 3.7 • 58.3% grad student • average year: 1.3 • 58.3% ME • 41.7% BME + 1 BioE i am taking this class because • I am interested in cells • I am interested in mechanics • I want to learn how to describe cells mechanically • I want to learn how the mechanical environment influences the cell cell mechanics is primarily part of my... • 29.2% research • 87.5% coursework the inner life of a cell, viel & lue, harvard [2006] me239 mechanics of the cell 1 me239 mechanics of the cell 2 me239 statistics me239 statistics background in cell biology and mechanics what particular cells are you interested in and why... • cells mostly undergrad coursework (75.0%), high school classes. some have • cardiomyocytes ... clinical implications, prevalence of cardiac disease taken graduate level classes (12.5%) and done research related to cell biology • stem cells ... potential benefit for patients suffering from numerous conditions • mechanics almost all have a solid mechanics background from either under- • read blood cells ... i think they are cool graduate degrees (75.0%) or graduate classes (25.0%). • neural cells ... i love the brain • skin cells, bone cells, cartilage cells three equations that you consider most important in mechanics • hooks law / more generally constitutive equations which scales are you most interested in? • 12.5% cellular scale and smaller • newton’s second law – more generally equilibrium equations • 45.8% cellular scale -
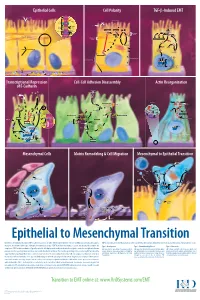
Epithelial to Mesenchymal Transition
Epithelial Cells Cell Polarity TGF-b-Induced EMT MUC-1 O-glycosylation Epithelial Cells ZO-1 Occludin Apical Membrane Tight F-Actin Microvilli Junction Claudin F-Actin p120 β-Catenin Adherens F-Actin Ezrin TGF-β dimer Junction E-Cadherin α-Catenin Plakophilin Crumbs Complex PAR Complex Desmocollin Desmoplakin Desmosome PtdIns(4,5)P2 TGF-β RII TGF-β RI CRB Cdc42Par6 Desmoglein Cytokeratin Pals1 PatJ Tight Junction Plakoglobin aPKC Par3 Domain Smad7 Extracellular PTEN JNK ERK1/2 p38 SARA Smurf1 Cortical Actin Cytoskeleton Space Par3 ZO-1 Adherens Junction PI 3-K Domain Smad-independent Signaling (–) Smad7 Translocation Smad2/3 PtdIns(3,4,5)P3 Smad4 Smad4 NEDD4 Cytokeratin Intermediate Filaments Smad2 Smad4 Smad3 LLGL Proteasome SCRIB DLG Scribble Complex Fibronectin Twist Smad2/3 Vitronectin ZEB 1/2 Microtubule Network Smad4 N-Cadherin Snail Basolateral Membrane CoA, Collagen I Slug CoR MMPs DNA-binding (+) Claudin Desmoplakin Transcription Factor Occludin Cytokeratins E-Cadherin Plakoglobin Integrins β α Nidogen-1/Entactin Perlecan Laminin Collagen IV Transcriptional Repression Cell-Cell Adhesion Disassembly Actin Reorganization of E-Cadherin TGF-β dimer EGF TGF-β RII TGF-β RI IGF FGF Receptor TNF-α Tyrosine Kinase Par6 TNF RI Apical Focal Adhesion Constriction Actin Depolymerization F-Actin Smurf1 Occludin Wnt Frizzled Myosin II Ras RhoA α-Actinin Myosin II ROCK AxinCK1 Dishevelled GSK-3 PI 3-K Src Zyxin MLC Phosphatase APC Proteasome FAK Vinculin RhoA ILK Talin (Inactive) Hakai Talin FAK F-Actin E-Cadherin LIMK Akt Paxillin FAK Stress -

Quantitative Methodologies to Dissect Immune Cell Mechanobiology
cells Review Quantitative Methodologies to Dissect Immune Cell Mechanobiology Veronika Pfannenstill 1 , Aurélien Barbotin 1 , Huw Colin-York 1,* and Marco Fritzsche 1,2,* 1 Kennedy Institute for Rheumatology, University of Oxford, Roosevelt Drive, Oxford OX3 7LF, UK; [email protected] (V.P.); [email protected] (A.B.) 2 Rosalind Franklin Institute, Harwell Campus, Didcot OX11 0FA, UK * Correspondence: [email protected] (H.C.-Y.); [email protected] (M.F.) Abstract: Mechanobiology seeks to understand how cells integrate their biomechanics into their function and behavior. Unravelling the mechanisms underlying these mechanobiological processes is particularly important for immune cells in the context of the dynamic and complex tissue microen- vironment. However, it remains largely unknown how cellular mechanical force generation and mechanical properties are regulated and integrated by immune cells, primarily due to a profound lack of technologies with sufficient sensitivity to quantify immune cell mechanics. In this review, we discuss the biological significance of mechanics for immune cells across length and time scales, and highlight several experimental methodologies for quantifying the mechanics of immune cells. Finally, we discuss the importance of quantifying the appropriate mechanical readout to accelerate insights into the mechanobiology of the immune response. Keywords: mechanobiology; biomechanics; force; immune response; quantitative technology Citation: Pfannenstill, V.; Barbotin, A.; Colin-York, H.; Fritzsche, M. Quantitative Methodologies to Dissect 1. Introduction Immune Cell Mechanobiology. Cells The development of novel quantitative technologies and their application to out- 2021, 10, 851. https://doi.org/ standing scientific problems has often paved the way towards ground-breaking biological 10.3390/cells10040851 findings. -

A Computational Study of Stress Fiber-Focal Adhesion Dynamics
A computational study of stress fiber-focal adhesion dynamics governing cell contractility M. Maraldi1, C. Valero2, K. Garikipati1;3∗ 1Department of Mechanical Engineering, University of Michigan, Ann Arbor, Michigan 2M2BE, Aragon´ Institute of Engineering Research (I3A), University of Zaragoza, Zaragoza, Spain 3Department of Mathematics, University of Michigan, Ann Arbor, Michigan Abstract We apply a recently developed model of cytoskeletal force generation to study a cell’s intrinsic contractility, as well as its response to external loading. The model is based on a non-equilibrium thermodynamic treatment of the mechano-chemistry governing force in the stress fiber-focal adhesion system. Our computational study suggests that the mechan- ical coupling between the stress fibers and focal adhesions leads to a complex, dynamic, mechano-chemical response. We collect the results in response maps whose regimes are distinguished by the initial geometry of the stress fiber-focal adhesion system, and by the external load on the cell. The results from our model connect qualitatively with recent stud- ies on the force response of smooth muscle cells on arrays of polymeric microposts (Mann et al., Lab. on a Chip, 12, 731-740, 2012). INTRODUCTION In contractile cells, such as smooth muscle cells and fibroblasts, the generation of traction force is the result of two different actions: myosin-powered cytoskeletal contractility and external mechanical stimuli (applied stretch or force). The cooperation between these two aspects de- termines the level of the force within the cell and influences the development of cytoskeletal components via the (un)binding of proteins. Important cytoskeletal components that mediate this interplay of mechanics and chemistry are stress fibers and focal adhesions. -

Cell Mechanics: from Cytoskeletal Dynamics to Tissue-Scale Mechanical Phenomena
Syracuse University SURFACE Physics - Dissertations College of Arts and Sciences 5-2013 Cell Mechanics: From Cytoskeletal Dynamics to Tissue-Scale Mechanical Phenomena Shiladitya Banerjee Follow this and additional works at: https://surface.syr.edu/phy_etd Recommended Citation Banerjee, Shiladitya, "Cell Mechanics: From Cytoskeletal Dynamics to Tissue-Scale Mechanical Phenomena" (2013). Physics - Dissertations. 131. https://surface.syr.edu/phy_etd/131 This Dissertation is brought to you for free and open access by the College of Arts and Sciences at SURFACE. It has been accepted for inclusion in Physics - Dissertations by an authorized administrator of SURFACE. For more information, please contact [email protected]. Syracuse University SUrface Physics - Dissertations College of Arts and Sciences 5-1-2013 Cell Mechanics: From Cytoskeletal Dynamics to Tissue-Scale Mechanical Phenomena Shiladitya Banerjee [email protected] Follow this and additional works at: http://surface.syr.edu/phy_etd Recommended Citation Banerjee, Shiladitya, "Cell Mechanics: From Cytoskeletal Dynamics to Tissue-Scale Mechanical Phenomena" (2013). Physics - Dissertations. Paper 131. This Dissertation is brought to you for free and open access by the College of Arts and Sciences at SUrface. It has been accepted for inclusion in Physics - Dissertations by an authorized administrator of SUrface. For more information, please contact [email protected]. Abstract This dissertation explores the mechanics of living cells, integrating the role of intracellular activity to capture the emergent mechanical behav- ior of cells. The topics covered in this dissertation fall into three broad categories : (a) intracellular mechanics, (b) interaction of cells with the extracellular matrix and (c) collective mechanics of multicellular colonies. In part (a) I propose theoretical models for motor-filament interactions in the cell cytoskeleton, which is the site for mechanical force generation in cells. -

Endothelial Cadherin Endothelium Is Regulated by Vascular Progenitor
Migration of Human Hematopoietic Progenitor Cells Across Bone Marrow Endothelium Is Regulated by Vascular Endothelial Cadherin This information is current as of October 1, 2021. Jaap D. van Buul, Carlijn Voermans, Veronique van den Berg, Eloise C. Anthony, Frederik P. J. Mul, Sandra van Wetering, C. Ellen van der Schoot and Peter L. Hordijk J Immunol 2002; 168:588-596; ; doi: 10.4049/jimmunol.168.2.588 http://www.jimmunol.org/content/168/2/588 Downloaded from References This article cites 54 articles, 33 of which you can access for free at: http://www.jimmunol.org/content/168/2/588.full#ref-list-1 http://www.jimmunol.org/ Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision • No Triage! Every submission reviewed by practicing scientists • Fast Publication! 4 weeks from acceptance to publication by guest on October 1, 2021 *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2002 by The American Association of Immunologists All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. Migration of Human Hematopoietic Progenitor Cells Across Bone Marrow Endothelium Is Regulated by Vascular Endothelial Cadherin1 Jaap D. van Buul,* Carlijn Voermans,* Veronique van den Berg,* Eloise C. -

1 Introduction to Cell Biology
1 Introduction to cell biology 1.1 Motivation Why is the understanding of cell mechancis important? cells need to move and interact with their environment ◦ cells have components that are highly dependent on mechanics, e.g., structural proteins ◦ cells need to reproduce / divide ◦ to improve the control/function of cells ◦ to improve cell growth/cell production ◦ medical appli- cations ◦ mechanical signals regulate cell metabolism ◦ treatment of certain diseases needs understanding of cell mechanics ◦ cells live in a mechanical environment ◦ it determines the mechanics of organisms that consist of cells ◦ directly applicable to single cell analysis research ◦ to understand how mechanical loading affects cells, e.g. stem cell differentation, cell morphology ◦ to understand how mechanically gated ion channels work ◦ an understanding of the loading in cells could aid in developing struc- tures to grow cells or organization of cells more efficiently ◦ can help us to understand macrostructured behavior better ◦ can help us to build machines/sensors similar to cells ◦ can help us understand the biology of the cell ◦ cell growth is affected by stress and mechanical properties of the substrate the cells are in ◦ understanding mechan- ics is important for knowing how cells move and for figuring out how to change cell motion ◦ when building/engineering tissues, the tissue must have the necessary me- chanical properties ◦ understand how cells is affected by and affects its environment ◦ understand how mechanical factors alter cell behavior (gene expression) -

A Review of Single-Cell Adhesion Force Kinetics and Applications
cells Review A Review of Single-Cell Adhesion Force Kinetics and Applications Ashwini Shinde 1 , Kavitha Illath 1, Pallavi Gupta 1, Pallavi Shinde 1, Ki-Taek Lim 2 , Moeto Nagai 3 and Tuhin Subhra Santra 1,* 1 Department of Engineering Design, Indian Institute of Technology Madras, Chennai 600036, Tamil Nadu, India; [email protected] (A.S.); [email protected] (K.I.); [email protected] (P.G.); [email protected] (P.S.) 2 Department of Biosystems Engineering, Kangwon National University, Chuncheon-Si, Gangwon-Do 24341, Korea; [email protected] 3 Department of Mechanical Engineering, Toyohashi University of Technology, 1-1 Hibarigaoka, Tempaku-cho, Toyohashi, Aichi 441-8580, Japan; [email protected] * Correspondence: [email protected]; Tel.: +91-044-2257-4747 Abstract: Cells exert, sense, and respond to the different physical forces through diverse mechanisms and translating them into biochemical signals. The adhesion of cells is crucial in various develop- mental functions, such as to maintain tissue morphogenesis and homeostasis and activate critical signaling pathways regulating survival, migration, gene expression, and differentiation. More impor- tantly, any mutations of adhesion receptors can lead to developmental disorders and diseases. Thus, it is essential to understand the regulation of cell adhesion during development and its contribution to various conditions with the help of quantitative methods. The techniques involved in offering different functionalities such as surface imaging to detect forces present at the cell-matrix and deliver quantitative parameters will help characterize the changes for various diseases. Here, we have briefly reviewed single-cell mechanical properties for mechanotransduction studies using standard and recently developed techniques. -

Emerging Views of the Nucleus As a Cellular Mechanosensor Tyler J
Emerging views of the nucleus as a cellular mechanosensor Tyler J. Kirby1,2 and Jan Lammerding1,2 1 Nancy E. and Peter C. Meinig School of Biomedical Engineering, Cornell University, Ithaca, New York 2 Weill Institute for Cell and Molecular Biology, Cornell University, Ithaca, New York Correspondence to: Jan Lammerding, PhD Cornell University Weill Institute for Cell and Molecular Biology Nancy E. and Peter C. Meinig School of Biomedical Engineering Weill Hall, Room 235 Ithaca, NY 14853 USA Abstract The ability of cells to respond to mechanical forces is critical for numerous biological processes. Emerging evidence indicates that external mechanical forces trigger changes in nuclear envelope structure and composition, chromatin organization, and gene expression. However, it remains unclear if these processes originate in the nucleus or are downstream of cytoplasmic signals. This review discusses recent findings supporting a direct role of the nucleus in cellular mechanosensing and highlights novel tools to study nuclear mechanotransduction. 1 Introduction Cells are constantly being exposed to mechanical forces, such as shear forces on endothelial cells1, compressive forces on chondrocytes2, and tensile forces in myocytes3. The cells’ ability to sense and respond to these mechanical cues are critical for numerous biological processes, including embryogenesis4, 5, development4, 5, and tissue homeostasis6, 7. While it has long been recognized that mechanical forces can influence cell morphology and behavior8, 9, the understanding of the -

Mitotic Cells Contract Actomyosin Cortex and Generate Pressure to Round Against Or Escape Epithelial Confinement
ARTICLE Received 28 Feb 2015 | Accepted 12 Oct 2015 | Published 25 Nov 2015 DOI: 10.1038/ncomms9872 OPEN Mitotic cells contract actomyosin cortex and generate pressure to round against or escape epithelial confinement Barbara Sorce1, Carlos Escobedo1,2, Yusuke Toyoda3, Martin P. Stewart1,4,5, Cedric J. Cattin1, Richard Newton1, Indranil Banerjee6, Alexander Stettler1, Botond Roska6, Suzanne Eaton3, Anthony A. Hyman3, Andreas Hierlemann1 & Daniel J. Mu¨ller1 Little is known about how mitotic cells round against epithelial confinement. Here, we engineer micropillar arrays that subject cells to lateral mechanical confinement similar to that experienced in epithelia. If generating sufficient force to deform the pillars, rounding epithelial (MDCK) cells can create space to divide. However, if mitotic cells cannot create sufficient space, their rounding force, which is generated by actomyosin contraction and hydrostatic pressure, pushes the cell out of confinement. After conducting mitosis in an unperturbed manner, both daughter cells return to the confinement of the pillars. Cells that cannot round against nor escape confinement cannot orient their mitotic spindles and more likely undergo apoptosis. The results highlight how spatially constrained epithelial cells prepare for mitosis: either they are strong enough to round up or they must escape. The ability to escape from confinement and reintegrate after mitosis appears to be a basic property of epithelial cells. 1 Department of Biosystems Science and Engineering, Eidgeno¨ssische Technische Hochschule (ETH) Zurich, Mattenstrasse 26, Basel 4058, Switzerland. 2 Department of Chemical Engineering, Queen’s University, 19 Division Street, Kingston, Ontario, Canada K7L 3N6. 3 Max Planck Institute of Molecular Cell Biology and Genetics, Pfotenhauerstrasse 108, 01307 Dresden, Germany. -

A Comparison of Methods to Assess Cell Mechanical Properties
ANALYSIS https://doi.org/10.1038/s41592-018-0015-1 A comparison of methods to assess cell mechanical properties Pei-Hsun Wu1*, Dikla Raz-Ben Aroush2, Atef Asnacios 3*, Wei-Chiang Chen1, Maxim E. Dokukin4, Bryant L. Doss5, Pauline Durand-Smet3, Andrew Ekpenyong6, Jochen Guck 6*, Nataliia V. Guz7, Paul A. Janmey2*, Jerry S. H. Lee1,8, Nicole M. Moore9, Albrecht Ott10*, Yeh-Chuin Poh9, Robert Ros5*, Mathias Sander10, Igor Sokolov 4*, Jack R. Staunton 5, Ning Wang9*, Graeme Whyte6 and Denis Wirtz 1* The mechanical properties of cells influence their cellular and subcellular functions, including cell adhesion, migration, polar- ization, and differentiation, as well as organelle organization and trafficking inside the cytoplasm. Yet reported values of cell stiffness and viscosity vary substantially, which suggests differences in how the results of different methods are obtained or analyzed by different groups. To address this issue and illustrate the complementarity of certain approaches, here we present, analyze, and critically compare measurements obtained by means of some of the most widely used methods for cell mechanics: atomic force microscopy, magnetic twisting cytometry, particle-tracking microrheology, parallel-plate rheom- etry, cell monolayer rheology, and optical stretching. These measurements highlight how elastic and viscous moduli of MCF-7 breast cancer cells can vary 1,000-fold and 100-fold, respectively. We discuss the sources of these variations, including the level of applied mechanical stress, the rate of deformation, the geometry of the probe, the location probed in the cell, and the extracellular microenvironment. ells in vivo are continuously subjected to mechanical forces, seven different technologies, including atomic force microscopy including shear, compressive, and extensional forces (Fig. -

Ventral Stress Fibers Induce Plasma Membrane Deformation in Human Fibroblasts
bioRxiv preprint doi: https://doi.org/10.1101/2021.03.01.433420; this version posted March 2, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. Ventral Stress Fibers Induce Plasma Membrane Deformation in Human Fibroblasts Samuel J. Ghilardi1,2, Mark S. Aronson1,2, and Allyson E. Sgro1,2 1Department of Biomedical Engineering 2Biological Design Center, Boston University, Boston, MA 02215 USA Abstract actions, actin stress fibers deform the membrane at smaller Interactions between the actin cytoskeleton and the plasma structures such as focal adhesions (27, 28) and filopodia, membrane are essential for many eukaryotic cellular processes. as well as in larger projections like lamellipodia (29–31). During these processes, actin fibers deform the cell membrane outward by applying forces parallel to the fiber’s major axis (as To deform the plasma membrane, actin stress fibers apply in migration) or they deform the membrane inward by applying force along their principle axis, either through actin polymer- forces perpendicular to the fiber’s major axis (as during cytoki- ization (32–34) or via myosin II contraction (35–38). As a nesis). Here we describe a novel actin-membrane interaction result, during most contractile events, actin stress fibers gen- in human dermal myofibroblasts. When labeled with a cytoso- erally deform the membrane parallel to the major axis of the lic fluorophore, the myofibroblasts developed prominent fluores- fiber. A notable exception to this is during specialized mem- cent structures on the ventral side of the cell.