Cell Mechanics and Mechanobiology
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Melanoma in the Eyes of Mechanobiology
fcell-08-00054 February 11, 2020 Time: 16:43 # 1 REVIEW published: 11 February 2020 doi: 10.3389/fcell.2020.00054 Melanoma in the Eyes of Mechanobiology M. Manuela Brás1,2,3, Manfred Radmacher4*, Susana R. Sousa1,2,5 and Pedro L. Granja1,2,3† 1 Instituto de Investigação e Inovação em Saúde, Universidade do Porto, Porto, Portugal, 2 Instituto de Engenharia Biomédica, Universidade do Porto, Porto, Portugal, 3 Faculdade de Engenharia, Universidade do Porto, Porto, Portugal, 4 Institute for Biophysics, University of Bremen, Bremen, Germany, 5 Instituto Superior de Engenharia do Porto, Instituto Politécnico do Porto, Porto, Portugal Skin is the largest organ of the human body with several important functions that can be impaired by injury, genetic or chronic diseases. Among all skin diseases, melanoma is one of the most severe, which can lead to death, due to metastization. Mechanotransduction has a crucial role for motility, invasion, adhesion and metastization processes, since it deals with the response of cells to physical forces. Signaling Edited by: pathways are important to understand how physical cues produced or mediated Shamik Sen, by the Extracellular Matrix (ECM), affect healthy and tumor cells. During these Indian Institute of Technology Bombay, India processes, several molecules in the nucleus and cytoplasm are activated. Melanocytes, Reviewed by: keratinocytes, fibroblasts and the ECM, play a crucial role in melanoma formation. This Zhizhan Gu, manuscript will address the synergy among melanocytes, keratinocytes, fibroblasts cells Dana-Farber Cancer Institute, United States and the ECM considering their mechanical contribution and relevance in this disease. Takashi Kato, Mechanical properties of melanoma cells can also be influenced by pigmentation, Johns Hopkins University, which can be associated with changes in stiffness. -
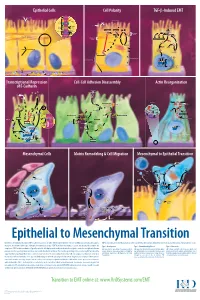
Epithelial to Mesenchymal Transition
Epithelial Cells Cell Polarity TGF-b-Induced EMT MUC-1 O-glycosylation Epithelial Cells ZO-1 Occludin Apical Membrane Tight F-Actin Microvilli Junction Claudin F-Actin p120 β-Catenin Adherens F-Actin Ezrin TGF-β dimer Junction E-Cadherin α-Catenin Plakophilin Crumbs Complex PAR Complex Desmocollin Desmoplakin Desmosome PtdIns(4,5)P2 TGF-β RII TGF-β RI CRB Cdc42Par6 Desmoglein Cytokeratin Pals1 PatJ Tight Junction Plakoglobin aPKC Par3 Domain Smad7 Extracellular PTEN JNK ERK1/2 p38 SARA Smurf1 Cortical Actin Cytoskeleton Space Par3 ZO-1 Adherens Junction PI 3-K Domain Smad-independent Signaling (–) Smad7 Translocation Smad2/3 PtdIns(3,4,5)P3 Smad4 Smad4 NEDD4 Cytokeratin Intermediate Filaments Smad2 Smad4 Smad3 LLGL Proteasome SCRIB DLG Scribble Complex Fibronectin Twist Smad2/3 Vitronectin ZEB 1/2 Microtubule Network Smad4 N-Cadherin Snail Basolateral Membrane CoA, Collagen I Slug CoR MMPs DNA-binding (+) Claudin Desmoplakin Transcription Factor Occludin Cytokeratins E-Cadherin Plakoglobin Integrins β α Nidogen-1/Entactin Perlecan Laminin Collagen IV Transcriptional Repression Cell-Cell Adhesion Disassembly Actin Reorganization of E-Cadherin TGF-β dimer EGF TGF-β RII TGF-β RI IGF FGF Receptor TNF-α Tyrosine Kinase Par6 TNF RI Apical Focal Adhesion Constriction Actin Depolymerization F-Actin Smurf1 Occludin Wnt Frizzled Myosin II Ras RhoA α-Actinin Myosin II ROCK AxinCK1 Dishevelled GSK-3 PI 3-K Src Zyxin MLC Phosphatase APC Proteasome FAK Vinculin RhoA ILK Talin (Inactive) Hakai Talin FAK F-Actin E-Cadherin LIMK Akt Paxillin FAK Stress -

Quantitative Methodologies to Dissect Immune Cell Mechanobiology
cells Review Quantitative Methodologies to Dissect Immune Cell Mechanobiology Veronika Pfannenstill 1 , Aurélien Barbotin 1 , Huw Colin-York 1,* and Marco Fritzsche 1,2,* 1 Kennedy Institute for Rheumatology, University of Oxford, Roosevelt Drive, Oxford OX3 7LF, UK; [email protected] (V.P.); [email protected] (A.B.) 2 Rosalind Franklin Institute, Harwell Campus, Didcot OX11 0FA, UK * Correspondence: [email protected] (H.C.-Y.); [email protected] (M.F.) Abstract: Mechanobiology seeks to understand how cells integrate their biomechanics into their function and behavior. Unravelling the mechanisms underlying these mechanobiological processes is particularly important for immune cells in the context of the dynamic and complex tissue microen- vironment. However, it remains largely unknown how cellular mechanical force generation and mechanical properties are regulated and integrated by immune cells, primarily due to a profound lack of technologies with sufficient sensitivity to quantify immune cell mechanics. In this review, we discuss the biological significance of mechanics for immune cells across length and time scales, and highlight several experimental methodologies for quantifying the mechanics of immune cells. Finally, we discuss the importance of quantifying the appropriate mechanical readout to accelerate insights into the mechanobiology of the immune response. Keywords: mechanobiology; biomechanics; force; immune response; quantitative technology Citation: Pfannenstill, V.; Barbotin, A.; Colin-York, H.; Fritzsche, M. Quantitative Methodologies to Dissect 1. Introduction Immune Cell Mechanobiology. Cells The development of novel quantitative technologies and their application to out- 2021, 10, 851. https://doi.org/ standing scientific problems has often paved the way towards ground-breaking biological 10.3390/cells10040851 findings. -

A Computational Study of Stress Fiber-Focal Adhesion Dynamics
A computational study of stress fiber-focal adhesion dynamics governing cell contractility M. Maraldi1, C. Valero2, K. Garikipati1;3∗ 1Department of Mechanical Engineering, University of Michigan, Ann Arbor, Michigan 2M2BE, Aragon´ Institute of Engineering Research (I3A), University of Zaragoza, Zaragoza, Spain 3Department of Mathematics, University of Michigan, Ann Arbor, Michigan Abstract We apply a recently developed model of cytoskeletal force generation to study a cell’s intrinsic contractility, as well as its response to external loading. The model is based on a non-equilibrium thermodynamic treatment of the mechano-chemistry governing force in the stress fiber-focal adhesion system. Our computational study suggests that the mechan- ical coupling between the stress fibers and focal adhesions leads to a complex, dynamic, mechano-chemical response. We collect the results in response maps whose regimes are distinguished by the initial geometry of the stress fiber-focal adhesion system, and by the external load on the cell. The results from our model connect qualitatively with recent stud- ies on the force response of smooth muscle cells on arrays of polymeric microposts (Mann et al., Lab. on a Chip, 12, 731-740, 2012). INTRODUCTION In contractile cells, such as smooth muscle cells and fibroblasts, the generation of traction force is the result of two different actions: myosin-powered cytoskeletal contractility and external mechanical stimuli (applied stretch or force). The cooperation between these two aspects de- termines the level of the force within the cell and influences the development of cytoskeletal components via the (un)binding of proteins. Important cytoskeletal components that mediate this interplay of mechanics and chemistry are stress fibers and focal adhesions. -

Endothelial Cadherin Endothelium Is Regulated by Vascular Progenitor
Migration of Human Hematopoietic Progenitor Cells Across Bone Marrow Endothelium Is Regulated by Vascular Endothelial Cadherin This information is current as of October 1, 2021. Jaap D. van Buul, Carlijn Voermans, Veronique van den Berg, Eloise C. Anthony, Frederik P. J. Mul, Sandra van Wetering, C. Ellen van der Schoot and Peter L. Hordijk J Immunol 2002; 168:588-596; ; doi: 10.4049/jimmunol.168.2.588 http://www.jimmunol.org/content/168/2/588 Downloaded from References This article cites 54 articles, 33 of which you can access for free at: http://www.jimmunol.org/content/168/2/588.full#ref-list-1 http://www.jimmunol.org/ Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision • No Triage! Every submission reviewed by practicing scientists • Fast Publication! 4 weeks from acceptance to publication by guest on October 1, 2021 *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2002 by The American Association of Immunologists All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. Migration of Human Hematopoietic Progenitor Cells Across Bone Marrow Endothelium Is Regulated by Vascular Endothelial Cadherin1 Jaap D. van Buul,* Carlijn Voermans,* Veronique van den Berg,* Eloise C. -

Mechanobiology of Migrating Cells from Basic Science to the Clinic
A COST Action CA15214 (EuroCellNet) Working Group Meeting Mechanobiology of Migrating Cells From Basic Science to the Clinic 1st – 2nd April 2019 Venue Department of Physics Rua Larga, University of Coimbra 2 Coimbra 2019 Monday, 1st April 09.45 - 10.00 WELCOME AND INTRODUCTION Keynote Speaker 10.00 – 10.40 M. Ángela Nieto, Instituto de Neurociencias (CSIC-UMH), Alicante, Spain “Epithelial plasticity in health and disease (the INs and OUTs of the EMT)” ECM and Cell Migration Session Chair: Nuno Saraiva 10.40 – 11.00 Florence Janody, University of Porto, Portugal “Computational modelling and experimental approaches identify a role of ECM stiffening in Src- induces EMT” 11.00 - 11.20 Juan Carlos Rodríguez-Manzaneque, GENYO, Granada, Spain “Relevance of ECM proteolytic remodelling for cell invasion and migration” 11.20 - 11.40 Rui Travasso, University of Coimbra, Portugal “Mathematical modelling of migrating cells and angiogenesis” 11.40 - 12.00 María José Oliveira, University of Porto, Portugal “Decellularized human colorectal cancer matrices as a tumor microenvironment biomimetic model” 12.00 – 14.00 Lunch Justiça e Paz, Couraça de Lisboa, 30 Keynote Speaker 14.00 - 14.40 Lino Ferreira, University of Coimbra, Portugal “Mechanical forces in vascular cell maturation and disease” 4 Coimbra 2019 Mechanotransduction and Cytoskeleton Session Chair: Ana Fernandes 14.40 - 15.00 Mirjana Liovic, Medical Center for Molecular Biology, Institute for Biochemistry, Faculty of Medicine, University of Ljubljana, Ljubljana, Slovenia “Cytoskeletal mutations -

Integrated Micro/Nanoengineered Functional Biomaterials for Cell Mechanics and Mechanobiology: REVIEW a Materials Perspective
www.advmat.de www.MaterialsViews.com Integrated Micro/Nanoengineered Functional Biomaterials for Cell Mechanics and Mechanobiology: REVIEW A Materials Perspective Yue Shao and Jianping Fu * which actively signals to cells to regulate The rapid development of micro/nanoengineered functional biomaterials in their fate and function. The microenviron- the last two decades has empowered materials scientists and bioengineers mental factors, including cell-cell inter- to precisely control different aspects of the in vitro cell microenvironment. actions, soluble factors such as oxygen tension and growth factors, and adhesive Following a philosophy of reductionism, many studies using synthetic and biophysical interactions between functional biomaterials have revealed instructive roles of individual extra- cells and extracellular matrix (ECM), are cellular biophysical and biochemical cues in regulating cellular behaviors. all important for regulation of cellular Development of integrated micro/nanoengineered functional biomaterials behaviors. Cells and the surrounding to study complex and emergent biological phenomena has also thrived microenvironment can also dynamically infl uence each other during normal devel- rapidly in recent years, revealing adaptive and integrated cellular behaviors opment, tissue homeostasis and repair, closely relevant to human physiological and pathological conditions. Working and progression of diseases through their at the interface between materials science and engineering, biology, and reciprocal biochemical and biophysical medicine, we are now at the beginning of a great exploration using micro/ interactions. [ 1–6 ] Thus, a detailed appre- nanoengineered functional biomaterials for both fundamental biology study hension and understanding of cell-micro- and clinical and biomedical applications such as regenerative medicine and environment interactions is critical for both advancing basic biology knowledge drug screening. -

Modeling the Mechanobiology of Cancer Cell Migration Using 3D Biomimetic Hydrogels
gels Review Modeling the Mechanobiology of Cancer Cell Migration Using 3D Biomimetic Hydrogels Xabier Morales †, Iván Cortés-Domínguez † and Carlos Ortiz-de-Solorzano * IDISNA, Ciberonc and Solid Tumors and Biomarkers Program, Center for Applied Medical Research, University of Navarra, 31008 Pamplona, Spain; [email protected] (X.M.); [email protected] (I.C.-D.) * Correspondence: [email protected] † These authors contributed equally to this work. Abstract: Understanding how cancer cells migrate, and how this migration is affected by the me- chanical and chemical composition of the extracellular matrix (ECM) is critical to investigate and possibly interfere with the metastatic process, which is responsible for most cancer-related deaths. In this article we review the state of the art about the use of hydrogel-based three-dimensional (3D) scaffolds as artificial platforms to model the mechanobiology of cancer cell migration. We start by briefly reviewing the concept and composition of the extracellular matrix (ECM) and the materials commonly used to recreate the cancerous ECM. Then we summarize the most relevant knowledge about the mechanobiology of cancer cell migration that has been obtained using 3D hydrogel scaf- folds, and relate those discoveries to what has been observed in the clinical management of solid tumors. Finally, we review some recent methodological developments, specifically the use of novel bioprinting techniques and microfluidics to create realistic hydrogel-based models of the cancer ECM, and some of their applications in the context of the study of cancer cell migration. Keywords: hydrogel; collagen; Matrigel; extracellular matrix; mechanobiology; amoeboid-mesenchymal transition; cancer; cell migration; microfluidic devices; bioprinting Citation: Morales, X.; Cortés-Domínguez, I.; Ortiz-de-Solorzano, C. -

Ventral Stress Fibers Induce Plasma Membrane Deformation in Human Fibroblasts
bioRxiv preprint doi: https://doi.org/10.1101/2021.03.01.433420; this version posted March 2, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. Ventral Stress Fibers Induce Plasma Membrane Deformation in Human Fibroblasts Samuel J. Ghilardi1,2, Mark S. Aronson1,2, and Allyson E. Sgro1,2 1Department of Biomedical Engineering 2Biological Design Center, Boston University, Boston, MA 02215 USA Abstract actions, actin stress fibers deform the membrane at smaller Interactions between the actin cytoskeleton and the plasma structures such as focal adhesions (27, 28) and filopodia, membrane are essential for many eukaryotic cellular processes. as well as in larger projections like lamellipodia (29–31). During these processes, actin fibers deform the cell membrane outward by applying forces parallel to the fiber’s major axis (as To deform the plasma membrane, actin stress fibers apply in migration) or they deform the membrane inward by applying force along their principle axis, either through actin polymer- forces perpendicular to the fiber’s major axis (as during cytoki- ization (32–34) or via myosin II contraction (35–38). As a nesis). Here we describe a novel actin-membrane interaction result, during most contractile events, actin stress fibers gen- in human dermal myofibroblasts. When labeled with a cytoso- erally deform the membrane parallel to the major axis of the lic fluorophore, the myofibroblasts developed prominent fluores- fiber. A notable exception to this is during specialized mem- cent structures on the ventral side of the cell. -

A Novel Role for Cadherin-11
Mechanobiology of Cardiac Disease and Fibrosis: a Novel Role for Cadherin-11 By Alison Koelle Schroer Dissertation Submitted to the Faculty of the Graduate School of Vanderbilt University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in Biomedical Engineering December, 2016 Nashville, Tennessee Approved: W. David Merryman, Ph.D. John Wikswo, Ph.D. Michael Miga, Ph.D. Jeffrey Davidson, Ph.D. Antonis Hatzopoulos, Ph.D. Copyright © 2016 by Alison K Schroer All Rights Reserved ii ACKNOWLEDGEMENTS The heart has its reasons, of which reason knows nothing - Pascal I must acknowledge my coauthors on the manuscripts which have been adapted and included in this dissertation. First and foremost, my advisor Dave Merryman. Also Larisa Rhyzhova, Cyndi Clark, Hind Lal, Qinkun Zhang, Tom Force, John Wikswo, Veniamin Sidorov, Matthew Shotwell, Annabelle Manalo, and David Bader. I would also acknowledge Josh Bender and Claire Lafferty, undergraduate research assistants who assisted in the collection of some of the data included in this work. I would also like to acknowledge Meghan Bowler, Mark Vander Roest, Caleb Snider, Allison Price, and Jeffrey Davidson for their editorial comments on the work included in this dissertation. I would like to acknowledge my funding sources, especially the NSF and the AHA. Also, the ever wonderful Merryman Lab, members both past and present, who have been my comrades and friends throughout the last five years. Finally, I must acknowledge my family, my friends, and my God, without whom I never could have done all this. Keep your heart with all vigilance, for from it flow the springs of life. -

Cellular Mechanobiology of Glioblastoma Multiforme
Cellular Mechanobiology of Glioblastoma Multiforme by Theresa Ann Ulrich A dissertation submitted in partial satisfaction of the requirements of the degree of Joint Doctor of Philosophy with University of California, San Francisco in Bioengineering in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Sanjay Kumar, Chair Professor Mohammad Mofrad Professor Tejal Desai Professor Andrew Wurmser Spring 2011 Cellular Mechanobiology of Glioblastoma Multiforme © 2011 By Theresa Ann Ulrich Abstract Cellular Mechanobiology of Glioblastoma Multiforme by Theresa Ann Ulrich Joint Doctor of Philosophy in Bioengineering with University of California, San Francisco University of California, Berkeley Professor Sanjay Kumar, Chair The rapid progression of high-grade brain tumors is related to diffuse infiltration of single tumor cells into the surrounding brain parenchyma, a process that involves aberrant interactions between tumor cells and the extracellular matrix (ECM). Tremendous effort has been devoted to elucidating the genetic and biochemical underpinnings of these tumors; however, poor translation of candidate therapies from animal models to human patients has only increased the sense of urgency for the development of new approaches in both the laboratory and the clinic. Indeed, despite decades of extensive clinical and biological research, the life expectancy of patients with grade IV glioblastoma multiforme (GBM) brain tumors is still approximately one year at diagnosis. The work presented in this dissertation has approached this problem from a biophysical perspective, demonstrating that biomechanical cues from the ECM serve as regulators of key GBM tumor cell properties relevant to invasion in both two-dimensional (2D) and three-dimensional (3D) culture models. We first investigated the role of ECM rigidity in regulating the structure, migration, and proliferation of a panel of glioma cell lines on 2D fibronectin-coated polymeric ECM substrates of defined mechanical rigidity. -

Wang (2006) Mechanobiology of Tendon.Pdf
ARTICLE IN PRESS Journal of Biomechanics 39 (2006) 1563–1582 www.elsevier.com/locate/jbiomech www.JBiomech.com Review Mechanobiology of tendon James H.-C. Wangà MechanoBiology Laboratory, Departments of Orthopaedic Surgery, Bioengineering and Mechanical Engineering, University of Pittsburgh, 210 Lothrop St., BST, E1647, Pittsburgh, PA 15213, USA Accepted 11 May 2005 Abstract Tendons are able to respond to mechanical forces by altering their structure, composition, and mechanical properties—a process called tissue mechanical adaptation. The fact that mechanical adaptation is effected by cells in tendons is clearly understood; however, how cells sense mechanical forces and convert them into biochemical signals that ultimately lead to tendon adaptive physiological or pathological changes is not well understood. Mechanobiology is an interdisciplinary study that can enhance our understanding of mechanotransduction mechanisms at the tissue, cellular, and molecular levels. The purpose of this article is to provide an overview of tendon mechanobiology. The discussion begins with the mechanical forces acting on tendons in vivo, tendon structure and composition, and its mechanical properties. Then the tendon’s response to exercise, disuse, and overuse are presented, followed by a discussion of tendon healing and the role of mechanical loading and fibroblast contraction in tissue healing. Next, mechanobiological responses of tendon fibroblasts to repetitive mechanical loading conditions are presented, and major cellular mechanotransduction mechanisms are briefly reviewed. Finally, future research directions in tendon mechanobiology research are discussed. r 2005 Elsevier Ltd. All rights reserved. Keywords: Tendon; Mechanobiology; Mechanical adaptation; Tendon fibroblasts; Mechanotransduction Contents 1. Introduction . 1564 2. Tendon forces in vivo . 1564 3. Tendon structure, composition, and mechanical properties .