DOCSLIB.ORG

Discrete Mathematics (Math 510) — Fall 2014 Definitions and Theorems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Mathematics (Math 510) — Fall 2014 Definitions and Theorems Discrete Mathematics (Math 510) — Fall 2014 Definitions and Theorems Gerald Hoehn October 12, 2014 Chapter 1 Graph Theory 1.1 Basics Definition 1.1. A graph G is an ordered pair (V,E) of disjoint finite sets such that E is a subset of the set of unordered pairs of V . We call V = V (G) the vertices of G and E = E(G) the edges of G. An edge {x, y} in E is said to join the vertices x and y and denoted by xy. We call x and y the end-vertices of the edge xy. Two vertices x and y are called adjacent if xy is an edge of G. The order of G is the cardinality of V , the size of G is the cardinality of E. Definition 1.2. A complete graph is a graph in which all distinct vertices are adjacent. The complete graph of order n is denoted by Kn. Definition 1.3. A empty graph is a graph without edges. The empty graph of order n is denoted by En. Definition 1.4. The complement G of a graph G is the graph with the same vertex set as G, and whose edge set consists of all edges not present in G. Definition 1.5. Cycle on n vertices, Cn; defined by picture (vertices v1, ..., vn, edges v1v2, v2v3, ..., vn−1vn, vnv1). Definition 1.6. Path on n-vertices, Pn; defined by picture (vertices v1, ..., vn, edges v1v2, v2v3, ..., vn−1vn). Definition 1.7. A graph G is bipartite if its vertex set can be partitioned into two sets X and Y such that every edge of G has one end vertex in X and the other in Y . The complete bipartite graph K|X|,|Y | is the graph with vertex set V = · X S Y and edge set E = {xy | x ∈ X, y ∈ Y }. Definition 1.8. Two graphs G and H are said to be isomorphic if there exists a one-to-one correspondence f : V (G) −→ V (H) such for each pair of vertices x, y ∈ V (G) one has xy ∈ E(G) if and only if f(x)f(y) ∈ E(H). One calls f an isomorphism. 1 “Isomorphic” is a precise way to say that we “ignore” the labels of the vertices. Definition 1.9. We say that a graph H is a subgraph of a graph G if V (H) ⊂ V (G) and E(H) ⊂ E(G). We also say that H is a subgraph if H is isomorphic to a subgraph in the above sense. Definition 1.10. For G a graph and v a vertex the degree deg(v) is the number of edges with end-vertex v. We let δ(G) be the minimal and ∆(G) be the maximal degree of any vertex of G. Theorem 1.1. The sum of the degrees of the vertices is equal to twice the numbers of edges: deg(v) = 2 ·|E(G)|. v∈V (G) Definition 1.11. A walk in a graph is a sequence of vertices v1, v2, ..., vk such that vivi+1 is an edge for each i = 1, ..., k − 1. A path is a walk in which all vertices are distinct. A cycle is path v1, ..., vk where k ≥ 3 and vkv1 is also an edge. The length of a walk, path or cycle is the number of corresponding edges. Theorem 1.2. If in a graph there exists a walk from u to v, then there exists also a path from u to v. Definition 1.12. Let G be a graph. For an edge e of G, G − e is the graph with the same vertices and all edges besides e. For an vertex v of G, G − v is the graph obtained by removing v and all edges ending in v. Definition 1.13. A graph is called connected if every two vertices can be joined by a path. Otherwise it is called disconnected. Note that every graph is the disjoint union of connected components. Definition 1.14. The connectivity κ(G) of a graph G is the minimal num- ber of vertices v1, ..., vk one has to choose such that G − {v1,...,vk} is disconnected. A graph is called k-connected if k ≤ κ(G). Note that a graph is connected if and only if κ(G) ≥ 1, i.e., G is 1- connected. Theorem 1.3. A graph is bipartite if and only if it contains no cycle of odd length. 2 1.2 Distance General assumption in this section: G is connected. Definition 1.15. Let u, v be two vertices of a graph G. The distance between u and v is the length of the shortest path connecting u with v and denoted by dG(u,v) or just d(u,v). This implies that d(u,u) = 0 for any vertex u. Definition 1.16. The diameter of a graph G, denoted diam(G), is the greatest distance between any two vertices: diam(G)= max d(u,v). u,v∈V (G) Theorem 1.4. On has: (i) d(u,v) ≥ 0 for all u, v and d(u,v) = 0 if and only if u = v. (ii) d(u,v)= d(v,u) for all u, v. (iii) d(u,w) ≤ d(u,v)+ d(v,w) for all u, v, w. Theorem 1.5. Let u be any vertex in a graph G. Let m be the maximal distance between u and any other vertex. Then m ≤ diam(G) ≤ 2m. Definition 1.17. Let G be a graph with vertices v1, ..., vn. The adjacency matrix of G is the n × n matrix whose (i,j) entry, denoted by [A]i,j, is defined by 1, if vi and vj are adjacent, [A]i,j = 0, otherwise. For graphs (without loops) the entries on the diagonal of A are zero. The matrix is symmetric, i.e., [A]i,j =[A]j,i for all i and j. Definition 1.18. Let A and B two n × n matrices. The product matrix A · B is the n × n matrix with entries [A · B]i,j =[A]i,1 · [B]1,j +[A]i,2 · [B]2,j + ··· +[A]i,n · [B]n,j. We set shortly A2 = A · A and Ak = Ak−1 · A for k ≥ 2. Theorem 1.6. Let G be a graph with vertices v1, v2, ..., vn and correspond- ing adjacency matrix A. Then for any positive integer k, the (i,j) entry of k A equals the number of walks from vi to vj that use exactly k edges. Corollary: Let G be a graph with vertices v1, v2, ..., vn and corresponding k adjacency matrix A. If d(vi,vj)= m, then [A ]i,j = 0 for 1 ≤ k < m. 3 Definition 1.19. For an n × n matrix A and a positive integer k set 2 k Sk = I + A + A + ··· + A where I is the identity matrix: 1 0 ... 0 0 0 1 ... 0 0 . I = . 0 0 ... 1 0 0 0 ... 0 1 . Theorem 1.7. Let G be a graph with vertices v1, ..., vn. If m is the smallest positive integer such that all entries of Sm are positive, then diam(G)= m. 1.3 Trees Definition 1.20. • A forest is a graph containing no cycles as subgraphs. • A tree is a connected forest. • A leave is a vertex of degree 1 in a tree. Theorem 1.8. A tree T of order n has n − 1 edges. Theorem 1.9. A graph of order n is a tree if and only if it is connected and contains n − 1 edges. Theorem 1.10. A graph of order n is a tree if and only if it contains no cycles and contains n − 1 edges. Theorem 1.11 (Cayley’s Tree formula). There are nn−2 distinct labeled trees of order n. Definition 1.21. A Pruefer seqence of a labeled tree is a sequence a1, a2, ..., an−2 of numbers from {1, 2,...,n} assigned in a unique way to a tree. (See the book for the precise algorithm.) A labeled tree can be uniquely reconstructed from its Pruefer sequence. (See the book for the precise algorithm.) Definition 1.22. The degree matrix of a graph G is the n × n matrix D defined by deg(vi), if i = j, [D]i,j = 0, else. Definition 1.23. Given an n × n-matrix M, the (i,j)-cofactor of M is defined to be (−1)i+jdet(M(i|j)) where det(M(i|j)) is the determinant of the (n − 1) × (n − 1)-matrix one gets by deleting the i-th row and the j-th column from M. 4 Theorem 1.12 (Matrix Tree Theorem (Kirchhoff)). Let G be a connected labeled graph with adjacency matrix A and degree matrix D. Then the num- ber of unique spanning trees of G is equal to the value of any cofactor of the matrix D − A. 1.4 Eulerian and Hamiltonian walks Eulerian trails and circuits Definition 1.24. Let G be a graph. A trail in G is a walk that does not repeat any edges. A closed trail is called a circuit. A cycle is a circuit. Definition 1.25. An Eulerian trail (resp. Eulerian circuit) in a graph G is a trail (resp. circuit) in G which includes every edge. A graph that contains an Eulerian circuit is said to be an Eulerian graph. Theorem 1.13. For a connected graph G the following statements are equiv- alent: (1) G is Eulerian.
Load more

Recommended publications
  • Regular Non-Hamiltonian Polyhedral Graphs
    Regular Non-Hamiltonian Polyhedral Graphs Nico VAN CLEEMPUT∗y and Carol T. ZAMFIRESCU∗zx July 2, 2018 Abstract. Invoking Steinitz' Theorem, in the following a polyhedron shall be a 3-connected planar graph. From around 1880 till 1946 Tait's conjecture that cu- bic polyhedra are hamiltonian was thought to hold|its truth would have implied the Four Colour Theorem. However, Tutte gave a counterexample. We briefly survey the ensuing hunt for the smallest non-hamiltonian cubic polyhedron, the Lederberg-Bos´ak-Barnettegraph, and prove that there exists a non-hamiltonian essentially 4-connected cubic polyhedron of order n if and only if n ≥ 42. This ex- tends work of Aldred, Bau, Holton, and McKay. We then present our main results which revolve around the quartic case: combining a novel theoretical approach for determining non-hamiltonicity in (not necessarily planar) graphs of connectivity 3 with computational methods, we dramatically improve two bounds due to Zaks. In particular, we show that the smallest non-hamiltonian quartic polyhedron has at least 35 and at most 39 vertices, thereby almost reaching a quartic analogue of a famous result of Holton and McKay. As an application of our results, we obtain that the shortness coefficient of the family of all quartic polyhedra does not exceed 5=6. The paper ends with a discussion of the quintic case in which we tighten a result of Owens. Keywords. Non-hamiltonian; non-traceable; polyhedron; planar; 3-connected; regular graph MSC 2010. 05C45, 05C10, 05C38 1 Introduction Due to Steinitz' classic theorem that the 1-skeleta of 3-polytopes are exactly the 3-connected planar graphs [34], we shall call such a graph a polyhedron.
    [Show full text]
  • Animation Visualization for Vertex Coloring of Polyhedral Graphs
    Animation Visualization for Vertex Coloring of Polyhedral Graphs Hidetoshi NONAKA Graduate School of Information Science and Technology, Hokkaido University Sapporo, 060 0814, Japan In this paper, we introduce a learning subsystem of interactive ABSTRACT vertex coloring, edge coloring, and face coloring, based on minimum spanning tree and degenerated polyhedron. Vertex Vertex coloring of a graph is the assignment of labels to the coloring of polyhedral graph itself is trivial in a mathematical vertices of the graph so that adjacent vertices have different labels. sense, and it is not novel also in a practical sense. However, In the case of polyhedral graphs, the chromatic number is 2, 3, or 4. visibility and interactivity can be helpful for the user to understand Edge coloring problem and face coloring problem can be intuitively the mathematical structure and the computational converted to vertex coloring problem for appropriate polyhedral scheme, by visualizing the process of the calculation, and by graphs. allowing the user to contribute the computation. We have been developed an interactive learning system of polyhedra, based on graph operations and simulated elasticity potential method, mainly for educational purpose. 2. POLYHEDRON MODELING SYTEM In this paper, we introduce a learning subsystem of vertex coloring, edge coloring and face coloring, based on minimum spanning tree In this section, we summarize the system of interactive modeling and degenerated polyhedron, which is introduced in this paper. of polyhedra described in [6-10]. It consists of three subsystems: graph input subsystem, wire-frame subsystem, and polygon Keywords: Vertex Coloring, Polyhedral Graph, Animation, subsystem. Visualization, Interactivity Graph Input Subsystem Figure 1(a) shows a screen shot of graph input subsystem, where a 1.
    [Show full text]
  • Upper Bound Constructions for Untangling Planar Geometric Graphs∗
    Upper bound constructions for untangling planar geometric graphs∗ Javier Canoy Csaba D. T´othz Jorge Urrutiax Abstract For every n 2 N, we construct an n-vertex planar graph G = (V; E), and n distinct points p(v), v 2 V , in the plane such that in any crossing-free straight-line drawing of G, at most :4948 O(pn ) vertices v 2 V are embedded at points p(v). This improves on an earlier bound of O( n) by Goaoc et al. [10]. 1 Introduction V A graph G = (V; E) is defined by a vertex set V and an edge set E ⊆ 2 .A straight-line 2 drawing of a graph G = (V; E) is a mapping p : V ! R of the vertices into distinct points in the plane, which induces a mapping of the edges fu; vg 2 E to line segments p(u)p(v) between the corresponding points. A straight-line drawing is crossing-free if no two edges intersect, except perhaps at a common endpoint. By F´ary'stheorem [9], a graph is planar if and only if it admits a crossing-free straight-line drawing. 2 Suppose we are given a planar graph G = (V; E) and a straight-line drawing p : V ! R (in which some edges may cross each other). Since G is planar, we can obtain a crossing-free straight- 0 2 line drawing p : V ! R by moving some of the vertices to new positions in the plane. The process 2 0 2 of changing a drawing p : V ! R to a crossing-free drawing p : V ! R is called an untangling 0 of (G; p).
    [Show full text]
  • 5 Graph Theory
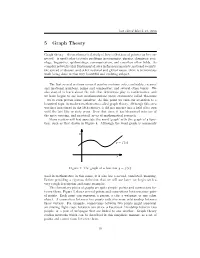
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • Operation-Based Notation for Archimedean Graph
    Operation-Based Notation for Archimedean Graph Hidetoshi Nonaka Research Group of Mathematical Information Science Division of Computer Science, Hokkaido University N14W9, Sapporo, 060 0814, Japan ABSTRACT Table 1. The list of Archimedean solids, where p, q, r are the number of vertices, edges, and faces, respectively. We introduce three graph operations corresponding to Symbol Name of polyhedron p q r polyhedral operations. By applying these operations, thirteen Archimedean graphs can be generated from Platonic graphs that A(3⋅4)2 Cuboctahedron 12 24 14 are used as seed graphs. A4610⋅⋅ Great Rhombicosidodecahedron 120 180 62 A468⋅⋅ Great Rhombicuboctahedron 48 72 26 Keyword: Archimedean graph, Polyhedral graph, Polyhedron A 2 Icosidodecahedron 30 60 32 notation, Graph operation. (3⋅ 5) A3454⋅⋅⋅ Small Rhombicosidodecahedron 60 120 62 1. INTRODUCTION A3⋅43 Small Rhombicuboctahedron 24 48 26 A34 ⋅4 Snub Cube 24 60 38 Archimedean graph is a simple planar graph isomorphic to the A354 ⋅ Snub Dodecahedron 60 150 92 skeleton or wire-frame of the Archimedean solid. There are A38⋅ 2 Truncated Cube 24 36 14 thirteen Archimedean solids, which are semi-regular polyhedra A3⋅102 Truncated Dodecahedron 60 90 32 and the subset of uniform polyhedra. Seven of them can be A56⋅ 2 Truncated Icosahedron 60 90 32 formed by truncation of Platonic solids, and all of them can be A 2 Truncated Octahedron 24 36 14 formed by polyhedral operations defined as Conway polyhedron 4⋅6 A 2 Truncated Tetrahedron 12 18 8 notation [1-2]. 36⋅ The author has recently developed an interactive modeling system of uniform polyhedra including Platonic solids, Archimedean solids and Kepler-Poinsot solids, based on graph drawing and simulated elasticity, mainly for educational purpose [3-5].
    [Show full text]
  • Barnette's Conjecture Arxiv:1310.5504V1 [Math.CO] 21
    Radboud Universiteit Nijmegen Barnette's Conjecture arXiv:1310.5504v1 [math.CO] 21 Oct 2013 Authors: Supervisor: Lean Arts Wieb Bosma Meike Hopman Veerle Timmermans October 22, 2013 Abstract This report provides an overview of theorems and statements related to a conjecture stated by D. W. Barnette in 1969. Barnettes conjecture is an open problem in graph theory about Hamiltonicity of graphs. Conjecture 0.1 (Barnettes conjecture). Every cubic, bipartite, polyhedral graph contains a Hamiltonian cycle. We will have a look Steinitzs theorem, which allows to reformulate the conjecture. We look at the complexity of previous, related, conjectures and determine some necessary conditions for a Barnette graph to contain a Hamiltonian cycle. We will also determine some sufficient conditions for a graph to contain a Hamiltonian cycle. We will give a sketch of the proof for Barnettes conjecture for graphs up to 64 vertices and we will describe two operations by which all Barnette graphs can be constructed. Finally, we will describe some programs in C++ that will help to check some properties in graphs, like bipartiteness, 3-connectedness and Hamiltonicity. Contents 1 Introduction 3 1.1 Preliminaries . .4 2 Steinitz's Theorem 6 3 Tait's Conjecture 9 3.1 Tutte's counterexample . .9 3.2 Smaller counterexamples . 11 3.3 Four color theorem for cubic 3-connected planar graphs . 11 4 Tutte's Conjecture 13 4.1 Horton fragment . 13 4.1.1 Horton-96 . 16 4.1.2 Horton-92 . 17 4.2 Ellingham Fragment . 18 5 Complexity 20 5.1 Tait's conjecture and the necessity of bipartiteness .
    [Show full text]
  • Graph Theory Graph Theory (III)
    J.A. Bondy U.S.R. Murty Graph Theory (III) ABC J.A. Bondy, PhD U.S.R. Murty, PhD Universite´ Claude-Bernard Lyon 1 Mathematics Faculty Domaine de Gerland University of Waterloo 50 Avenue Tony Garnier 200 University Avenue West 69366 Lyon Cedex 07 Waterloo, Ontario, Canada France N2L 3G1 Editorial Board S. Axler K.A. Ribet Mathematics Department Mathematics Department San Francisco State University University of California, Berkeley San Francisco, CA 94132 Berkeley, CA 94720-3840 USA USA Graduate Texts in Mathematics series ISSN: 0072-5285 ISBN: 978-1-84628-969-9 e-ISBN: 978-1-84628-970-5 DOI: 10.1007/978-1-84628-970-5 Library of Congress Control Number: 2007940370 Mathematics Subject Classification (2000): 05C; 68R10 °c J.A. Bondy & U.S.R. Murty 2008 Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or trans- mitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licenses issued by the Copyright Licensing Agency. Enquiries concerning reproduction outside those terms should be sent to the publishers. The use of registered name, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant laws and regulations and therefore free for general use. The publisher makes no representation, express or implied, with regard to the accuracy of the information contained in this book and cannot accept any legal responsibility or liability for any errors or omissions that may be made.
    [Show full text]
  • 4-Regular 4-Connected Hamiltonian Graphs with Few Hamiltonian Cycles
    4-regular 4-connected Hamiltonian graphs with few Hamiltonian cycles Carsten THOMASSEN∗ and Carol T. ZAMFIRESCU† Abstract. We prove that there exists an infinite family of 4-regular 4- connected Hamiltonian graphs with a bounded number of Hamiltonian cy- cles. We do not know if there exists such a family of 5-regular 5-connected Hamiltonian graphs. Key words. Hamiltonian cycle; regular graph MSC 2020. 05C45; 05C07; 05C30 1 Introduction There is a variety of 3-regular 3-connected graphs with no Hamiltonian cycles. Much less is known about 4-regular 4-connected graphs. Thus the Petersen graph (on 10 vertices) is the smallest 3-regular 3-connected non-Hamiltonian graph whereas it was an open prob- lem of Nash-Williams if there exists a 4-regular 4-connected non-Hamiltonian graph until Meredith [9] gave an infinite family, the smallest of which has 70 vertices, see [1, p. 239]. Tait's conjecture that every 3-regular 3-connected graph has a Hamiltonian cycle was open from 1880 till Tutte [15] in 1946 found a counterexample, see [1, p. 161]. By Steinitz' the- orem, the Tutte graph (and subsequently many others) also show that there are infinitely many 3-regular 3-polyhedral graphs which are non-Hamiltonian, whereas it is a longstanding conjecture of Barnette that every 4-regular 4-polyhedral graph has a Hamiltonian cycle [5, p. 1145] (see also [6, p. 389a] and [4, p. 375]). There are infinitely many 3-regular hypohamil- tonian graphs whereas it is a longstanding open problem if there exists a hypohamiltonian graph of minimum degree at least 4, see [12].
    [Show full text]
  • Necessary Condition for Cubic Planar 3-Connected Graph to Be Non-Hamiltonian with Proof of Barnette’S Conjecture
    International J.Math. Combin. Vol.3(2014), 70-88 Necessary Condition for Cubic Planar 3-Connected Graph to be Non-Hamiltonian with Proof of Barnette’s Conjecture Mushtaq Ahmad Shah (Department of Mathematics, Vivekananda Global University (Formerly VIT Jaipur)) E-mail: [email protected] Abstract: A conjecture of Barnette states that, every three connected cubic bipartite pla- nar graph is Hamiltonian. This problem has remained open since its formulation. This paper has a threefold purpose. The first is to provide survey of literature surrounding the conjec- ture. The second is to give the necessary condition for cubic planar three connected graph to be non-Hamiltonian and finally, we shall prove near about 50 year Barnett’s conjecture. For the proof of different results using to prove the results we illustrate most of the results by using counter examples. Key Words: Cubic graph, hamiltonian cycle, planar graph, bipartite graph, faces, sub- graphs, degree of graph. AMS(2010): 05C25 §1. Introduction It is not an easy task to prove the Barnette’s conjecture by direct method because it is very difficult process to prove or disprove it by direct method. In this paper, we use alternative method to prove the conjecture. It must be noted that if any one property of the Barnette’s graph is deleted graph is non Hamiltonian. A planar graph is an undirected graph that can be embedded into the Euclidean plane without any crossings. A planar graph is called polyhedral if and only if it is three vertex connected, that is, if there do not exists two vertices the removal of which would disconnect the rest of the graph.
    [Show full text]
  • Realizing Graphs As Polyhedra
    Realizing Graphs as Polyhedra David Eppstein Recent Trends in Graph Drawing: Curves, Graphs, and Intersections California State University Northridge, September 2015 Outline I Convex polyhedra I Steinitz's theorem I Incremental realization I Lifting from planar drawings I Circle packing I Non-convex polyhedra I Four-dimensional polytopes Steinitz's theorem Graphs of 3d convex polyhedra = 3-vertex-connected planar graphs [Steinitz 1922] File:Uniform polyhedron-53-t0.svg and File:Graph of 20-fullerene w-nodes.svg from Wikimedia commons Polyhedral graphs are planar Projection from near one face gives a planar Schlegel diagram Alternatively, the polyhedral surface itself (minus one point) is topologically equivalent to a plane Polyhedral graphs are 3-connected Theorem [Balinski 1961]: d-dimensional polytopes are d-connected Proof idea: I Consider any set C of fewer than d vertices I Add one more vertex v I Find linear function f , zero on C [ fvg, nonzero elsewhere I Simplex method finds C-avoiding paths from v to both min f and max f , and from all other vertices to min or max I Therefore, C does not disconnect the graph Combinatorial uniqueness of realization Face cycles do not separate rest of graph: Any two points not on given face can be connected by a path disjoint from the face (same argument as Balinski) Non-face cycles do separate one side of cycle from the other (Jordan curve theorem) So faces are determined by graph structure Planar graphs that are not 3-connected can have multiple embeddings Polyhedral realization of 3-connected
    [Show full text]
  • A Computer-Assisted Proof of Barnette-Goodey Conjecture: Not
    A computer-assisted proof of Barnette-Goodey conjecture: Not only fullerene graphs are Hamiltonian. Frantiˇsek Kardoˇs LaBRI, University of Bordeaux, France [email protected] August 18, 2017 Abstract Fullerene graphs, i.e., 3-connected planar cubic graphs with pentagonal and hexag- onal faces, are conjectured to be Hamiltonian. This is a special case of a conjecture of Barnette and Goodey, stating that 3-connected planar graphs with faces of size at most 6 are Hamiltonian. We prove the conjecture. 1 Introduction Tait conjectured in 1880 that cubic polyhedral graphs (i.e., 3-connected planar cubic graphs) are Hamiltonian. The first counterexample to Tait’s conjecture was found by Tutte in 1946; later many others were found, see Figure 1. Had the conjecture been true, it would have implied the Four-Color Theorem. However, each known non-Hamiltonian cubic polyhedral graph has at least one face of size 7 or more [1, 17]. It was conjectured that all cubic polyhedral graphs with maximum face size at most 6 are Hamiltonian. In the literature, the conjecture is usually attributed to Barnette (see, e.g., [13]), however, Goodey [6] stated it in an informal way as well. This conjecture covers in particular the class of fullerene graphs, 3-connected cubic planar graphs with pentagonal and hexagonal faces only. Hamiltonicity was verified for all fullerene graphs with up to 176 vertices [1]. Later on, the conjecture in the general form was verified arXiv:1409.2440v2 [math.CO] 16 Aug 2017 for all graphs with up to 316 vertices [2]. On the other hand, cubic polyhedral graphs having only faces of sizes 3 and 6 or 4 and 6 are known to be Hamiltonian [6, 7].
    [Show full text]
  • Optimal Straight-Line Drawings of Non-Planar Graphs
    Ministry of Education and Science of Ukraine Ivan Franko National University of Lviv Faculty of Mechanics and Mathematics Department of Theory of Functions and Probability Theory Master thesis Optimal Straight-Line Drawings of Non-Planar Graphs Submitted by student of group MTM-62m Oksana Firman Supervisor Dr. Oleh Romaniv Scientific consultant Dr. Alexander Ravsky Lviv 2017 Contents Introduction 2 1 Drawing Graphs on Few Objects 6 2 Drawing Platonic Graphs 9 2.1 Placing Vertices of Platonic Graphs on Few Lines 2 1 in R (π2)........................................ 10 2.2 Placing Vertices of Platonic Graphs on Few Lines 3 1 in R (π3)........................................ 13 1 3 Graphs with Unbounded π2 14 Conclusion 20 References 20 1 Introduction Graph Drawing is an interesting subfield of Graph Theory. It is related to different aspects of science such as social network analysis, cartography, linguistics, and bioinformatics. Why it is so useful to research this area of mathematics and computer science? Graphs are used for solving different problems. Computational problems in industry are such. For example: traffic organization, social relations, artificial intelligence and so on. One real-world problem solved by graph theory is finding the shortest path between two given nodes. Shortest path algorithms are widely used due to their generality. We can find an optimal solution for given problem using graphs. One of the questions in this field is: which drawing of graph is the best for a given application. An (undirected) graph is a pair G = (V; E) where V is a set of vertices and E ⊆ ffu; vg ⊆ V j u 6= vg is a set of edges.
    [Show full text]