DOCSLIB.ORG

Enumeration of Polyhedral Graphs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Enumeration of Polyhedral Graphs Enumeration of Polyhedral Graphs Samuel George Kamperis Doctor of Philosophy Oxford Brookes University 2019 Declaration I declare that this thesis was composed by myself and that the work contained therein is my own, except where explicitly stated otherwise in the text. (Samuel George Kamperis) iii I owe so many, so much::: To my family and friends for their love and support throughout this process. I thank the staff at Oxford Brookes who have become such a big part of my life. Dr Rachel Long for her invaluable guidance and supervision, Professor Khaled Hayatleh and the rest of my supervisory team for their help over the years. To the PRS and the memory of Dr Alex (AJ) Boorman. My brother Ollie and the brotherhood of Josh and Louis Catlett. My sister Sophie and the \brotherhood" of Katy Stroud. My parents George and Michele, whose infinite patience and unconditional love have taught me the true meaning of infinity. My beloved grandmothers, the heads of my amazing family, Maureen Heathfield and the sorely missed Katrina Kamperis. The one who I met through this PhD and has been my dearest companion ever since, my darling, Aya ~. Kampo X iv Abstract This thesis is concerned with the design of a polyhedron enumeration algorithm. The approach taken focuses on specific classes of polyhedra and their graph theo- retic properties. This is then compared more broadly to other graph enumeration algorithms that are concerned with the same or a superset which includes these properties. An original and novel algorithm is contributed to this area. The approach taken divides the problem into prescribed vertex and face degree sequences for the graphs. Using a range of existence, ordered enumeration and isomorphism techniques, it finds all unique 4-regular, 3-connected planar graphs. The algo- rithm is a vertex addition algorithm which means that each result output at a given stage has a new vertex added. Other results from different stages are never required for further computation and comparison, hence the process is embarrass- ingly parallel. Therefore, the enumeration can be distributed optimally across a cluster of computers. This work has led to a successfully implemented algorithm which takes a different approach to its treatment of the class of 4-regular, 3-connected planar graphs. As such this has led to observations and theory about other classes of graphs and graph embeddings which relate to this research. v vi Samuel George Kamperis vi Contents Abstract v 1 Introduction 1 1.1 Motivation . 1 1.2 Thesis Outline . 1 2 Background 5 2.1 Introduction . 5 2.2 Polyhedra . 5 2.2.1 Definitions . 5 2.2.2 Euler's Formula . 6 2.3 Planar Graphs . 7 2.3.1 Definitions . 8 2.3.2 Kuratowski's Theorem . 12 2.3.3 Steinitz' Theorem . 13 2.3.4 Cauchy's Proof of Euler's Formula . 14 2.3.5 Tutte's Wheel Theorem . 14 2.3.6 Tutte Embedding . 16 2.4 Algorithms . 20 2.4.1 Havel-Hakimi and Erd}os-Gallai . 20 2.4.2 Duijvestijn and Federico . 24 2.4.3 Hopcroft and Tarjan . 25 2.4.4 Hopcroft and Wong . 26 2.4.5 Brinkmann and McKay . 26 2.5 Summary . 28 vii viii Samuel George Kamperis 3 4-regular 3-connected Planar Graphs 31 3.1 Introduction . 31 3.2 3-connected Graph Embeddings . 32 3.3 Exactly 2-vertex, 3-edge connected Graph Embeddings . 33 3.4 Decomposition . 34 3.5 3-vertex Connectivity Test . 39 3.6 Summary . 44 4 Algorithm Design 47 4.1 Introduction . 47 4.2 Definitions . 48 4.3 Outline . 53 4.4 Invariants . 56 4.5 Combinations and Banning . 57 4.5.1 Introduction . 57 4.5.2 Reverse Circular Permutations . 57 4.5.3 Cycles . 58 4.5.4 Vertex Degree Sets . 61 4.5.5 Bans from Vertex Labels . 63 4.6 Subgraph Mapping . 65 4.6.1 Subgraph Data Structure . 66 4.6.2 Subgraph Isomorphism Test . 67 4.7 Computational Complexity . 71 4.7.1 Reduction in Computation from Bans . 72 4.7.2 Reduction in Computation from Subgraph Mapping . 73 4.7.3 Overall Reduction in Computational Cost . 74 4.8 Results Generated by the Algorithm . 75 4.8.1 Introduction . 75 4.8.2 Comparison with Existing Algorithms . 76 4.8.3 Total Numbers of Duals of 4-Regular 3-Connected Planar Graphs . 77 4.8.4 Summary of Results . 81 viii Enumeration of Polyhedral Graphs ix 4.9 Summary . 81 5 Observations from the Data 83 5.1 Introduction . 83 5.2 Realisability of Prescribed Duals on a Vertex Degree Sequence . 84 5.2.1 Overview . 84 5.2.2 Definitions . 84 5.2.3 Theory . 87 5.2.4 2-vertex, 3-edge connectivity Counterexample . 88 5.2.5 Exclusions Found . 89 5.3 Realisability of Large Vertex Degrees with respect to Sequence Size 94 5.3.1 Overview . 94 5.3.2 Theory . 94 5.3.3 2-vertex, 3-edge connectivity Counterexample . 95 5.3.4 Exclusions Found . 95 5.4 Summary . 98 6 Future Work, Potential Applications and Conclusion 101 6.1 Future Work . 101 6.2 Potential Applications . 102 6.2.1 Existence Testing on Embedded Subgraphs . 102 6.2.2 Unfolding . 102 6.2.3 Truncating . 103 6.2.4 Fullerenes . 103 6.3 Conclusion . 104 References 107 A Enumeration Algorithm Results 111 ix x Samuel George Kamperis x List of Figures 1.1 Log plot of numbers of polyhedra p(n) with only quadrilateral faces and n vertices . 2 2.1 Square pyramids with vertices, edges & faces highlighted . 7 2.2 Non-convex polyhedra . 8 2.3 Graphs representing an octahedron . 10 2.4 Creating the dual of a planar embedding . 10 2.5 The non-planar graphs K5 and K3;3 . 13 2.6 Projections of a cube onto a plane . 15 2.7 Planar graph of a cube at different stages of Cauchy's proof of Euler's formula . 18 2.8 The different graphs resulting from vertex contraction and split- ting on a 5 spoke wheel, where an arrow represents the vertex contraction operation . 19 3.1 A wheel graph with 10 vertices and its polyhedral representation . 33 3.2 Two distinct embeddings of an exactly 2-vertex, 3-edge connected planar graph . 35 3.3 Bipartite graph with only quadrilateral faces . 36 3.4 Example graph with the face sharing vertices in V1 overlaid . 39 3.5 Decomposed graph embeddings . 39 3.6 Planar graph with one sided face . 40 3.7 Planar graphs with two sided faces . 41 3.8 2-edge connected planar graph . 41 3.9 Planar graph highlighting Case 1 . 42 xi xii Samuel George Kamperis 3.10 Planar graph highlighting Case 2 . 42 3.11 Planar graph highlighting Case 3 . 43 4.1 Range of permissible sizes for degree sequences by jV j . 52 4.2 Search tree of graph generation with degree sequences: f5; 4; 3; 3; 3; 3; 3g and f4; 4; 4; 3; 3; 3; 3g . 53 4.3 Search tree of graph generation with degree sequences: f5; 3; 3; 3; 3; 3g and f4; 4; 3; 3; 3; 3g . 54 4.4 Search tree of successful nodes in graph generation with degree sequences: f4; 4; 4; 4; 3; 3; 3; 3g and f4; 4; 4; 4; 3; 3; 3; 3g . 55 4.5 Graph example for optimised circular permutations . 63 4.6 Subgraph with adjacencies from Table 4.6 (node 27 on the search tree in Figure 4.2) . 64 4.7 Search tree for D1 = f4; 4; 4; 3; 3; 3; 3g and D2 = f4; 4; 4; 3; 3; 3; 3g 68 4.8 Subgraph at node 76 in D1 = f4; 4; 4; 3; 3; 3; 3g and D2 = f4; 4; 4; 3; 3; 3; 3g 69 4.9 Subgraph at node 78 in D1 = f4; 4; 4; 3; 3; 3; 3g and D2 = f4; 4; 4; 3; 3; 3; 3g 70 4.10 Subgraph at node 77 in D1 = f4; 4; 4; 3; 3; 3; 3g and D2 = f4; 4; 4; 3; 3; 3; 3g 71 4.11 A subgraph isomorphic to subgraph at node 77 in D1 = f4; 4; 4; 3; 3; 3; 3g and D2 = f4; 4; 4; 3; 3; 3; 3g ...................... 72 4.12 Example Graph A1 . 73 4.13 Example Graph B1 . 73 4.14 Example Graph A2 . 74 4.15 Example Graph B2 . 74 4.16 Graph Comparing CPU Time for Different Versions of the Code . 75 4.17 Graph of Number of Nodes Generated vs CPU Time Difference for Code Versions . 76 4.18 Graph Comparing Number of Nodes Generated for Different Ver- sions of the Code . 77 4.19 Graph Comparing Number of Nodes Generated with and without Optimisations of the Code . 78 4.20 Graph Comparing CPU Time with and without Optimisations of the Code . 79 xii Enumeration of Polyhedral Graphs xiii 5.1 Polygonal faces with complementary edges . 86 5.2 Counter example for 2-vertex 3-edge connected graphs . 88 5.3 Catchrate of degree sequence pairs for Test 1 . 91 5.4 Counter example for 2-vertex 3-edge connected graphs . 95 5.5 Catchrate of degree sequence pairs for Test 2 . ..
Load more

Recommended publications
  • Equivelar Octahedron of Genus 3 in 3-Space
    Equivelar octahedron of genus 3 in 3-space Ruslan Mizhaev ([email protected]) Apr. 2020 ABSTRACT . Building up a toroidal polyhedron of genus 3, consisting of 8 nine-sided faces, is given. From the point of view of topology, a polyhedron can be considered as an embedding of a cubic graph with 24 vertices and 36 edges in a surface of genus 3. This polyhedron is a contender for the maximal genus among octahedrons in 3-space. 1. Introduction This solution can be attributed to the problem of determining the maximal genus of polyhedra with the number of faces - . As is known, at least 7 faces are required for a polyhedron of genus = 1 . For cases ≥ 8 , there are currently few examples. If all faces of the toroidal polyhedron are – gons and all vertices are q-valence ( ≥ 3), such polyhedral are called either locally regular or simply equivelar [1]. The characteristics of polyhedra are abbreviated as , ; [1]. 2. Polyhedron {9, 3; 3} V1. The paper considers building up a polyhedron 9, 3; 3 in 3-space. The faces of a polyhedron are non- convex flat 9-gons without self-intersections. The polyhedron is symmetric when rotated through 1804 around the axis (Fig. 3). One of the features of this polyhedron is that any face has two pairs with which it borders two edges. The polyhedron also has a ratio of angles and faces - = − 1. To describe polyhedra with similar characteristics ( = − 1) we use the Euler formula − + = = 2 − 2, where is the Euler characteristic. Since = 3, the equality 3 = 2 holds true.
    [Show full text]
  • Regular Non-Hamiltonian Polyhedral Graphs
    Regular Non-Hamiltonian Polyhedral Graphs Nico VAN CLEEMPUT∗y and Carol T. ZAMFIRESCU∗zx July 2, 2018 Abstract. Invoking Steinitz' Theorem, in the following a polyhedron shall be a 3-connected planar graph. From around 1880 till 1946 Tait's conjecture that cu- bic polyhedra are hamiltonian was thought to hold|its truth would have implied the Four Colour Theorem. However, Tutte gave a counterexample. We briefly survey the ensuing hunt for the smallest non-hamiltonian cubic polyhedron, the Lederberg-Bos´ak-Barnettegraph, and prove that there exists a non-hamiltonian essentially 4-connected cubic polyhedron of order n if and only if n ≥ 42. This ex- tends work of Aldred, Bau, Holton, and McKay. We then present our main results which revolve around the quartic case: combining a novel theoretical approach for determining non-hamiltonicity in (not necessarily planar) graphs of connectivity 3 with computational methods, we dramatically improve two bounds due to Zaks. In particular, we show that the smallest non-hamiltonian quartic polyhedron has at least 35 and at most 39 vertices, thereby almost reaching a quartic analogue of a famous result of Holton and McKay. As an application of our results, we obtain that the shortness coefficient of the family of all quartic polyhedra does not exceed 5=6. The paper ends with a discussion of the quintic case in which we tighten a result of Owens. Keywords. Non-hamiltonian; non-traceable; polyhedron; planar; 3-connected; regular graph MSC 2010. 05C45, 05C10, 05C38 1 Introduction Due to Steinitz' classic theorem that the 1-skeleta of 3-polytopes are exactly the 3-connected planar graphs [34], we shall call such a graph a polyhedron.
    [Show full text]
  • A Theory of Nets for Polyhedra and Polytopes Related to Incidence Geometries
    Designs, Codes and Cryptography, 10, 115–136 (1997) c 1997 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. A Theory of Nets for Polyhedra and Polytopes Related to Incidence Geometries SABINE BOUZETTE C. P. 216, Universite´ Libre de Bruxelles, Bd du Triomphe, B-1050 Bruxelles FRANCIS BUEKENHOUT [email protected] C. P. 216, Universite´ Libre de Bruxelles, Bd du Triomphe, B-1050 Bruxelles EDMOND DONY C. P. 216, Universite´ Libre de Bruxelles, Bd du Triomphe, B-1050 Bruxelles ALAIN GOTTCHEINER C. P. 216, Universite´ Libre de Bruxelles, Bd du Triomphe, B-1050 Bruxelles Communicated by: D. Jungnickel Received November 22, 1995; Revised July 26, 1996; Accepted August 13, 1996 Dedicated to Hanfried Lenz on the occasion of his 80th birthday. Abstract. Our purpose is to elaborate a theory of planar nets or unfoldings for polyhedra, its generalization and extension to polytopes and to combinatorial polytopes, in terms of morphisms of geometries and the adjacency graph of facets. Keywords: net, polytope, incidence geometry, prepolytope, category 1. Introduction Planar nets for various polyhedra are familiar both for practical matters and for mathematical education about age 11–14. They are systematised in two directions. The most developed of these consists in the drawing of some net for each polyhedron in a given collection (see for instance [20], [21]). A less developed theme is to enumerate all nets for a given polyhedron, up to some natural equivalence. Little has apparently been done for polytopes in dimensions d 4 (see however [18], [3]). We have found few traces of this subject in the literature and we would be grateful for more references.
    [Show full text]
  • Animation Visualization for Vertex Coloring of Polyhedral Graphs
    Animation Visualization for Vertex Coloring of Polyhedral Graphs Hidetoshi NONAKA Graduate School of Information Science and Technology, Hokkaido University Sapporo, 060 0814, Japan In this paper, we introduce a learning subsystem of interactive ABSTRACT vertex coloring, edge coloring, and face coloring, based on minimum spanning tree and degenerated polyhedron. Vertex Vertex coloring of a graph is the assignment of labels to the coloring of polyhedral graph itself is trivial in a mathematical vertices of the graph so that adjacent vertices have different labels. sense, and it is not novel also in a practical sense. However, In the case of polyhedral graphs, the chromatic number is 2, 3, or 4. visibility and interactivity can be helpful for the user to understand Edge coloring problem and face coloring problem can be intuitively the mathematical structure and the computational converted to vertex coloring problem for appropriate polyhedral scheme, by visualizing the process of the calculation, and by graphs. allowing the user to contribute the computation. We have been developed an interactive learning system of polyhedra, based on graph operations and simulated elasticity potential method, mainly for educational purpose. 2. POLYHEDRON MODELING SYTEM In this paper, we introduce a learning subsystem of vertex coloring, edge coloring and face coloring, based on minimum spanning tree In this section, we summarize the system of interactive modeling and degenerated polyhedron, which is introduced in this paper. of polyhedra described in [6-10]. It consists of three subsystems: graph input subsystem, wire-frame subsystem, and polygon Keywords: Vertex Coloring, Polyhedral Graph, Animation, subsystem. Visualization, Interactivity Graph Input Subsystem Figure 1(a) shows a screen shot of graph input subsystem, where a 1.
    [Show full text]
  • Upper Bound Constructions for Untangling Planar Geometric Graphs∗
    Upper bound constructions for untangling planar geometric graphs∗ Javier Canoy Csaba D. T´othz Jorge Urrutiax Abstract For every n 2 N, we construct an n-vertex planar graph G = (V; E), and n distinct points p(v), v 2 V , in the plane such that in any crossing-free straight-line drawing of G, at most :4948 O(pn ) vertices v 2 V are embedded at points p(v). This improves on an earlier bound of O( n) by Goaoc et al. [10]. 1 Introduction V A graph G = (V; E) is defined by a vertex set V and an edge set E ⊆ 2 .A straight-line 2 drawing of a graph G = (V; E) is a mapping p : V ! R of the vertices into distinct points in the plane, which induces a mapping of the edges fu; vg 2 E to line segments p(u)p(v) between the corresponding points. A straight-line drawing is crossing-free if no two edges intersect, except perhaps at a common endpoint. By F´ary'stheorem [9], a graph is planar if and only if it admits a crossing-free straight-line drawing. 2 Suppose we are given a planar graph G = (V; E) and a straight-line drawing p : V ! R (in which some edges may cross each other). Since G is planar, we can obtain a crossing-free straight- 0 2 line drawing p : V ! R by moving some of the vertices to new positions in the plane. The process 2 0 2 of changing a drawing p : V ! R to a crossing-free drawing p : V ! R is called an untangling 0 of (G; p).
    [Show full text]
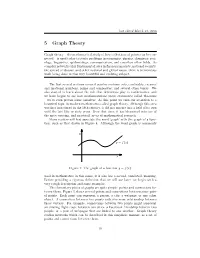
  • 5 Graph Theory
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • Zipper Unfoldings of Polyhedral Complexes
    Zipper Unfoldings of Polyhedral Complexes The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Demaine, Erik D. et al. "Zipper Unfoldings of Polyhedral Complexes." 22nd Canadian Conference on Computational Geometry, CCCG 2010, Winnipeg MB, August 9-11, 2010. As Published http://www.cs.umanitoba.ca/~cccg2010/accepted.html Publisher University of Manitoba Version Author's final manuscript Citable link http://hdl.handle.net/1721.1/62237 Terms of Use Creative Commons Attribution-Noncommercial-Share Alike 3.0 Detailed Terms http://creativecommons.org/licenses/by-nc-sa/3.0/ CCCG 2010, Winnipeg MB, August 9{11, 2010 Zipper Unfoldings of Polyhedral Complexes Erik D. Demaine∗ Martin L. Demainey Anna Lubiwz Arlo Shallitx Jonah L. Shallit{ Abstract We explore which polyhedra and polyhedral complexes can be formed by folding up a planar polygonal region and fastening it with one zipper. We call the reverse tetrahedron icosahedron process a zipper unfolding. A zipper unfolding of a polyhedron is a path cut that unfolds the polyhedron to a planar polygon; in the case of edge cuts, these are Hamiltonian unfoldings as introduced by Shephard in 1975. We show that all Platonic and Archimedean solids have Hamiltonian unfoldings. octahedron dodecahedron We give examples of polyhedral complexes that are, Figure 2: Doubly Hamiltonian unfoldings of the other and are not, zipper [edge] unfoldable. The positive ex- Platonic solids. amples include a polyhedral torus, and two tetrahedra joined at an edge or at a face. The physical model of a zipper provides a natural 1 Introduction extension of zipper unfolding to polyhedral complexes which generalize polyhedra, either by allowing positive A common way to build a paper model of a polyhe- genus (these are polyhedral manifolds), or by allowing dron is to fold and glue a planar polygonal shape, called an edge to be incident to more than two faces, or allow- a net of the polyhedron.
    [Show full text]
  • Representing the Sporadic Archimedean Polyhedra As Abstract Polytopes$
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector Discrete Mathematics 310 (2010) 1835–1844 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: www.elsevier.com/locate/disc Representing the sporadic Archimedean polyhedra as abstract polytopesI Michael I. Hartley a, Gordon I. Williams b,∗ a DownUnder GeoSolutions, 80 Churchill Ave, Subiaco, 6008, Western Australia, Australia b Department of Mathematics and Statistics, University of Alaska Fairbanks, PO Box 756660, Fairbanks, AK 99775-6660, United States article info a b s t r a c t Article history: We present the results of an investigation into the representations of Archimedean Received 29 August 2007 polyhedra (those polyhedra containing only one type of vertex figure) as quotients of Accepted 26 January 2010 regular abstract polytopes. Two methods of generating these presentations are discussed, Available online 13 February 2010 one of which may be applied in a general setting, and another which makes use of a regular polytope with the same automorphism group as the desired quotient. Representations Keywords: of the 14 sporadic Archimedean polyhedra (including the pseudorhombicuboctahedron) Abstract polytope as quotients of regular abstract polyhedra are obtained, and summarised in a table. The Archimedean polyhedron Uniform polyhedron information is used to characterize which of these polyhedra have acoptic Petrie schemes Quotient polytope (that is, have well-defined Petrie duals). Regular cover ' 2010 Elsevier B.V. All rights reserved. Flag action Exchange map 1. Introduction Much of the focus in the study of abstract polytopes has been on the regular abstract polytopes. A publication of the first author [6] introduced a method for representing any abstract polytope as a quotient of regular polytopes.
    [Show full text]
  • Of Rigid Motions) to Make the Simplest Possible Analogies Between Euclidean, Spherical,Toroidal and Hyperbolic Geometry
    SPHERICAL, TOROIDAL AND HYPERBOLIC GEOMETRIES MICHAEL D. FRIED, 231 MSTB These notes use groups (of rigid motions) to make the simplest possible analogies between Euclidean, Spherical,Toroidal and hyperbolic geometry. We start with 3- space figures that relate to the unit sphere. With spherical geometry, as we did with Euclidean geometry, we use a group that preserves distances. The approach of these notes uses the geometry of groups to show the relation between various geometries, especially spherical and hyperbolic. It has been in the background of mathematics since Klein’s Erlangen program in the late 1800s. I imagine Poincar´e responded to Klein by producing hyperbolic geometry in the style I’ve done here. Though the group approach of these notes differs philosophically from that of [?], it owes much to his discussion of spherical geometry. I borrowed the picture of a spherical triangle’s area directly from there. I especially liked how Henle has stereographic projection allow the magic multiplication of complex numbers to work for him. While one doesn’t need the rotation group in 3-space to understand spherical geometry, I used it gives a direct analogy between spherical and hyperbolic geometry. It is the comparison of the four types of geometry that is ultimately most inter- esting. A problem from my Problem Sheet has the name World Wallpaper. Map making is a subject that has attracted many. In our day of Landsat photos that cover the whole world in its great spherical presence, the still mysterious relation between maps and the real thing should be an easy subject for the classroom.
    [Show full text]
  • Operation-Based Notation for Archimedean Graph
    Operation-Based Notation for Archimedean Graph Hidetoshi Nonaka Research Group of Mathematical Information Science Division of Computer Science, Hokkaido University N14W9, Sapporo, 060 0814, Japan ABSTRACT Table 1. The list of Archimedean solids, where p, q, r are the number of vertices, edges, and faces, respectively. We introduce three graph operations corresponding to Symbol Name of polyhedron p q r polyhedral operations. By applying these operations, thirteen Archimedean graphs can be generated from Platonic graphs that A(3⋅4)2 Cuboctahedron 12 24 14 are used as seed graphs. A4610⋅⋅ Great Rhombicosidodecahedron 120 180 62 A468⋅⋅ Great Rhombicuboctahedron 48 72 26 Keyword: Archimedean graph, Polyhedral graph, Polyhedron A 2 Icosidodecahedron 30 60 32 notation, Graph operation. (3⋅ 5) A3454⋅⋅⋅ Small Rhombicosidodecahedron 60 120 62 1. INTRODUCTION A3⋅43 Small Rhombicuboctahedron 24 48 26 A34 ⋅4 Snub Cube 24 60 38 Archimedean graph is a simple planar graph isomorphic to the A354 ⋅ Snub Dodecahedron 60 150 92 skeleton or wire-frame of the Archimedean solid. There are A38⋅ 2 Truncated Cube 24 36 14 thirteen Archimedean solids, which are semi-regular polyhedra A3⋅102 Truncated Dodecahedron 60 90 32 and the subset of uniform polyhedra. Seven of them can be A56⋅ 2 Truncated Icosahedron 60 90 32 formed by truncation of Platonic solids, and all of them can be A 2 Truncated Octahedron 24 36 14 formed by polyhedral operations defined as Conway polyhedron 4⋅6 A 2 Truncated Tetrahedron 12 18 8 notation [1-2]. 36⋅ The author has recently developed an interactive modeling system of uniform polyhedra including Platonic solids, Archimedean solids and Kepler-Poinsot solids, based on graph drawing and simulated elasticity, mainly for educational purpose [3-5].
    [Show full text]
  • Barnette's Conjecture Arxiv:1310.5504V1 [Math.CO] 21
    Radboud Universiteit Nijmegen Barnette's Conjecture arXiv:1310.5504v1 [math.CO] 21 Oct 2013 Authors: Supervisor: Lean Arts Wieb Bosma Meike Hopman Veerle Timmermans October 22, 2013 Abstract This report provides an overview of theorems and statements related to a conjecture stated by D. W. Barnette in 1969. Barnettes conjecture is an open problem in graph theory about Hamiltonicity of graphs. Conjecture 0.1 (Barnettes conjecture). Every cubic, bipartite, polyhedral graph contains a Hamiltonian cycle. We will have a look Steinitzs theorem, which allows to reformulate the conjecture. We look at the complexity of previous, related, conjectures and determine some necessary conditions for a Barnette graph to contain a Hamiltonian cycle. We will also determine some sufficient conditions for a graph to contain a Hamiltonian cycle. We will give a sketch of the proof for Barnettes conjecture for graphs up to 64 vertices and we will describe two operations by which all Barnette graphs can be constructed. Finally, we will describe some programs in C++ that will help to check some properties in graphs, like bipartiteness, 3-connectedness and Hamiltonicity. Contents 1 Introduction 3 1.1 Preliminaries . .4 2 Steinitz's Theorem 6 3 Tait's Conjecture 9 3.1 Tutte's counterexample . .9 3.2 Smaller counterexamples . 11 3.3 Four color theorem for cubic 3-connected planar graphs . 11 4 Tutte's Conjecture 13 4.1 Horton fragment . 13 4.1.1 Horton-96 . 16 4.1.2 Horton-92 . 17 4.2 Ellingham Fragment . 18 5 Complexity 20 5.1 Tait's conjecture and the necessity of bipartiteness .
    [Show full text]
  • Graph Theory Graph Theory (III)
    J.A. Bondy U.S.R. Murty Graph Theory (III) ABC J.A. Bondy, PhD U.S.R. Murty, PhD Universite´ Claude-Bernard Lyon 1 Mathematics Faculty Domaine de Gerland University of Waterloo 50 Avenue Tony Garnier 200 University Avenue West 69366 Lyon Cedex 07 Waterloo, Ontario, Canada France N2L 3G1 Editorial Board S. Axler K.A. Ribet Mathematics Department Mathematics Department San Francisco State University University of California, Berkeley San Francisco, CA 94132 Berkeley, CA 94720-3840 USA USA Graduate Texts in Mathematics series ISSN: 0072-5285 ISBN: 978-1-84628-969-9 e-ISBN: 978-1-84628-970-5 DOI: 10.1007/978-1-84628-970-5 Library of Congress Control Number: 2007940370 Mathematics Subject Classification (2000): 05C; 68R10 °c J.A. Bondy & U.S.R. Murty 2008 Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or trans- mitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licenses issued by the Copyright Licensing Agency. Enquiries concerning reproduction outside those terms should be sent to the publishers. The use of registered name, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant laws and regulations and therefore free for general use. The publisher makes no representation, express or implied, with regard to the accuracy of the information contained in this book and cannot accept any legal responsibility or liability for any errors or omissions that may be made.
    [Show full text]