Necessary Condition for Cubic Planar 3-Connected Graph to Be Non-Hamiltonian with Proof of Barnette’S Conjecture
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

An Algorithm for Drawing Planar Graphs
An Algorithm for Drawing Planar Graphs Bor Plestenjak IMFMTCS University of Ljubljana Jadranska SI Ljubljana Slovenia email b orplestenjakfmfuniljsi AN ALGORITHM FOR DRAWING PLANAR GRAPHS SUMMARY A simple algorithm for drawing connected planar graphs is presented It is derived from the Fruchterman and Reingold spring emb edding algorithm by deleting all repulsive forces and xing vertices of an outer face The algorithm is implemented in the system for manipulating discrete mathematical structures Vega Some examples of derived gures are given Key words Planar graph drawing Forcedirected placement INTRODUCTION A graph G is planar if and only if it is p ossible to draw it in a plane without any edge intersections Every connected planar graph admits a convex drawing ie a planar drawing where every face is drawn as a convex p olygon We present a simple and ecient algorithm for convex drawing of a connected planar graph In addition to a graph most existing algorithms for planar drawing need as an input all the faces of a graph while our algorithm needs only one face of a graph to draw it planarly Let G b e a connected planar graph with a set of vertices V fv v g and a set of edges E 1 n fu v u v g Let W fw w w g V b e an ordered list of vertices of an arbitrary face in 1 1 m m 1 2 k graph G which is chosen for the outer face in the drawing The basic idea is as follows We consider graph G as a mechanical mo del by replacing its vertices with metal rings and its edges with elastic bands of zero length Vertices of the -

Regular Non-Hamiltonian Polyhedral Graphs
Regular Non-Hamiltonian Polyhedral Graphs Nico VAN CLEEMPUT∗y and Carol T. ZAMFIRESCU∗zx July 2, 2018 Abstract. Invoking Steinitz' Theorem, in the following a polyhedron shall be a 3-connected planar graph. From around 1880 till 1946 Tait's conjecture that cu- bic polyhedra are hamiltonian was thought to hold|its truth would have implied the Four Colour Theorem. However, Tutte gave a counterexample. We briefly survey the ensuing hunt for the smallest non-hamiltonian cubic polyhedron, the Lederberg-Bos´ak-Barnettegraph, and prove that there exists a non-hamiltonian essentially 4-connected cubic polyhedron of order n if and only if n ≥ 42. This ex- tends work of Aldred, Bau, Holton, and McKay. We then present our main results which revolve around the quartic case: combining a novel theoretical approach for determining non-hamiltonicity in (not necessarily planar) graphs of connectivity 3 with computational methods, we dramatically improve two bounds due to Zaks. In particular, we show that the smallest non-hamiltonian quartic polyhedron has at least 35 and at most 39 vertices, thereby almost reaching a quartic analogue of a famous result of Holton and McKay. As an application of our results, we obtain that the shortness coefficient of the family of all quartic polyhedra does not exceed 5=6. The paper ends with a discussion of the quintic case in which we tighten a result of Owens. Keywords. Non-hamiltonian; non-traceable; polyhedron; planar; 3-connected; regular graph MSC 2010. 05C45, 05C10, 05C38 1 Introduction Due to Steinitz' classic theorem that the 1-skeleta of 3-polytopes are exactly the 3-connected planar graphs [34], we shall call such a graph a polyhedron. -

Triple Connected Line Domination Number for Some Standard and Special Graphs
International Journal of Advanced Scientific Research and Management, Volume 3 Issue 8, Aug 2018 www.ijasrm.com ISSN 2455-6378 Triple Connected Line Domination Number For Some Standard And Special Graphs A.Robina Tony1, Dr. A.Punitha Tharani2 1 Research Scholar (Register Number: 12519), Department of Mathematics, St.Mary’s College(Autonomous), Thoothukudi – 628 001, Tamil Nadu, India, Affiliated to Manonmaniam Sundaranar University, Abishekapatti, Tirunelveli – 627 012, Tamil Nadu, India 2 Associate Professor, Department of Mathematics, St.Mary’s College(Autonomous), Thoothukudi – 628 001, Tamil Nadu, India, Affiliated to Manonmaniam Sundaranar University, Abishekapatti, Tirunelveli - 627 012, Tamil Nadu, India Abstract vertex domination, the concept of edge The concept of triple connected graphs with real life domination was introduced by Mitchell and application was introduced by considering the Hedetniemi. A set F of edges in a graph G is existence of a path containing any three vertices of a called an edge dominating set if every edge in E graph G. A subset S of V of a non - trivial graph G is – F is adjacent to at least one edge in F. The said to be a triple connected dominating set, if S is a dominating set and the induced subgraph <S> is edge domination number γ '(G) of G is the triple connected. The minimum cardinality taken minimum cardinality of an edge dominating set over all triple connected dominating set is called the of G. An edge dominating set F of a graph G is triple connected domination number and is denoted a connected edge dominating set if the edge by γtc(G). -

Minimal K-Connected Non-Hamiltonian Graphs
Graphs and Combinatorics (2018) 34:289–312 https://doi.org/10.1007/s00373-018-1874-z Minimal k-Connected Non-Hamiltonian Graphs Guoli Ding1 · Emily Marshall2 Received: 24 April 2017 / Revised: 31 January 2018 / Published online: 14 February 2018 © Springer Japan KK, part of Springer Nature 2018 Abstract In this paper, we explore minimal k-connected non-Hamiltonian graphs. Graphs are said to be minimal in the context of some containment relation; we focus on subgraphs, induced subgraphs, minors, and induced minors. When k = 2, we discuss all minimal 2-connected non-Hamiltonian graphs for each of these four rela- tions. When k = 3, we conjecture a set of minimal non-Hamiltonian graphs for the minor relation and we prove one case of this conjecture. In particular, we prove all 3-connected planar triangulations which do not contain the Herschel graph as a minor are Hamiltonian. Keywords Hamilton cycles · Graph minors 1 Introduction Hamilton cycles in graphs are cycles which visit every vertex of the graph. Determining their existence in a graph is an NP-complete problem and as such, there is a large body of research proving necessary and sufficient conditions. In this paper, we analyze non-Hamiltonian graphs. In particular, we consider the following general question: The first author was supported in part by NSF Grant DMS-1500699. The work for this paper was largely done while the second author was at Louisiana State University. B Emily Marshall [email protected] Guoli Ding [email protected] 1 Mathematics Department, Louisiana State University, Baton Rouge, LA 70803, USA 2 Computer Science and Mathematics Department, Arcadia University, Glenside, PA 19038, USA 123 290 Graphs and Combinatorics (2018) 34:289–312 what are the minimal k-connected non-Hamiltonian graphs? A graph is minimal if it does not contain a smaller graph with the same properties. -

Animation Visualization for Vertex Coloring of Polyhedral Graphs
Animation Visualization for Vertex Coloring of Polyhedral Graphs Hidetoshi NONAKA Graduate School of Information Science and Technology, Hokkaido University Sapporo, 060 0814, Japan In this paper, we introduce a learning subsystem of interactive ABSTRACT vertex coloring, edge coloring, and face coloring, based on minimum spanning tree and degenerated polyhedron. Vertex Vertex coloring of a graph is the assignment of labels to the coloring of polyhedral graph itself is trivial in a mathematical vertices of the graph so that adjacent vertices have different labels. sense, and it is not novel also in a practical sense. However, In the case of polyhedral graphs, the chromatic number is 2, 3, or 4. visibility and interactivity can be helpful for the user to understand Edge coloring problem and face coloring problem can be intuitively the mathematical structure and the computational converted to vertex coloring problem for appropriate polyhedral scheme, by visualizing the process of the calculation, and by graphs. allowing the user to contribute the computation. We have been developed an interactive learning system of polyhedra, based on graph operations and simulated elasticity potential method, mainly for educational purpose. 2. POLYHEDRON MODELING SYTEM In this paper, we introduce a learning subsystem of vertex coloring, edge coloring and face coloring, based on minimum spanning tree In this section, we summarize the system of interactive modeling and degenerated polyhedron, which is introduced in this paper. of polyhedra described in [6-10]. It consists of three subsystems: graph input subsystem, wire-frame subsystem, and polygon Keywords: Vertex Coloring, Polyhedral Graph, Animation, subsystem. Visualization, Interactivity Graph Input Subsystem Figure 1(a) shows a screen shot of graph input subsystem, where a 1. -

Packing by Edge Disjoint Trees
Global Journal of Mathematical Sciences: Theory and Practical. ISSN 0974-3200 Volume 5, Number 4 (2013), pp. 245_250 © International Research Publication House http://www.irphouse.com Packing by Edge Disjoint Trees Elachini V. Lal1 and Karakkattu S. Parvathy2 1Dept. of Higher Secondary, Govt. HSS Kuttippuram, Kerala INDIA– 679571. [email protected] 2Dept. of Mathematics, St. Mary’s College, Thrissur, Kerala INDIA – 680020. [email protected] Abstract A Graph G is said to be a packing by edge disjoint trees, if its edges can be partitioned into trees. In this paper, we discuss the packability of graphs of various types by edge disjoint tree and find its number w (edt G) and its least number wl (edt G) Key Words: Packing, Edge disjoint trees. 1. Introduction: By a graph G = (V, E) we mean a finite, undirected, connected graph with no loop or multiple edges. The order and size of G are denoted by ‘m’ and ‘n’ respectively. For basic graph theoretic terminology, we refer to [1, 2, 3]. The concept of random packability was introduced by Sergio Ruiz [4] under the name of ‘random decomposable graphs’. Ruiz [4] obtained a characterization of randomly F- packable graphs, when F is P3 or K2. Lowell W Beineke [5] and Peter Hamburger [5] and Wayne D Goddard [5] characterized F-packable graphs where F is Kn, P4, P5, or P6. S.Arumugham [6] and S.Meena [6] extended a characterization of the random packability of two or more disconnected graphs like Kn U K1, n, C4 U P2 ,3K2 .Elachini V. Lal [7] and Karakkattu S. -

Spindown Polyhedra
Spindown Polyhedra ANTHONY F. CONSTANTINIDES and GEORGE A. CONSTANTINIDES ARTICLE HISTORY Compiled March 20, 2018 1. Introduction Magic: The Gathering is a trading card game published by Wizards of the Coast [1]. The aim of most variants of the game is to reduce your opponent's life total from twenty to zero, thus winning the game. As it may take several turns to reduce a player's life total to zero, players need a mechanism to keep track of their current life total. For this purpose, players often use a device called a spindown life counter, shown in Figure 1. A spindown life counter is an icosahedron with a special labelling of the faces, such that - starting with 20 life total - a player can reduce their life total in decrements of one by rolling the icosahedron onto an adjacent face each time. A spindown life counter appears similar to a standard icosahedral die, known in gaming as a d20, however, the labelling of faces is different, as also shown in Figure 1. Figure 1. Left: A spindown life counter from Magic: The Gathering. Right: A standard icosahedral die (d20). The first author posed the question of whether it is possible to construct other polyhedra having a similar `spindown' property. Some simple experimentation revealed that is it possible to re-label the faces of a standard six-faced die (d6) to produce a spindown cube (see Figure 2); further experimentation revealed this to be the case for all Platonic solids. It can also be seen that it is possible, in all these cases, to chose the labelling such that it is not only spindown but also the face with the lowest label adjacent to the face with the highest label. -

Upper Bound Constructions for Untangling Planar Geometric Graphs∗
Upper bound constructions for untangling planar geometric graphs∗ Javier Canoy Csaba D. T´othz Jorge Urrutiax Abstract For every n 2 N, we construct an n-vertex planar graph G = (V; E), and n distinct points p(v), v 2 V , in the plane such that in any crossing-free straight-line drawing of G, at most :4948 O(pn ) vertices v 2 V are embedded at points p(v). This improves on an earlier bound of O( n) by Goaoc et al. [10]. 1 Introduction V A graph G = (V; E) is defined by a vertex set V and an edge set E ⊆ 2 .A straight-line 2 drawing of a graph G = (V; E) is a mapping p : V ! R of the vertices into distinct points in the plane, which induces a mapping of the edges fu; vg 2 E to line segments p(u)p(v) between the corresponding points. A straight-line drawing is crossing-free if no two edges intersect, except perhaps at a common endpoint. By F´ary'stheorem [9], a graph is planar if and only if it admits a crossing-free straight-line drawing. 2 Suppose we are given a planar graph G = (V; E) and a straight-line drawing p : V ! R (in which some edges may cross each other). Since G is planar, we can obtain a crossing-free straight- 0 2 line drawing p : V ! R by moving some of the vertices to new positions in the plane. The process 2 0 2 of changing a drawing p : V ! R to a crossing-free drawing p : V ! R is called an untangling 0 of (G; p). -
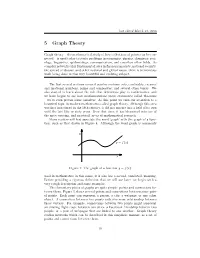
5 Graph Theory
last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples. -

On the Euclidean Dimension of Graphs
ON THE EUCLIDEAN DIMENSION OF GRAPHS JIN HYUP HONG GREAT NECK SOUTH HIGH SCHOOL, GREAT NECK, NY AND DAN ISMAILESCU MATHEMATICS DEPARTMENT, HOFSTRA UNIVERSITY, NY arXiv:1501.00204v1 [math.MG] 31 Dec 2014 1 Abstract. The Euclidean dimension a graph G is defined to be the smallest integer d such that the vertices of G can be located in Rd in such a way that two vertices are unit distance apart if and only if they are adjacent in G. In this paper we determine the Euclidean dimension for twelve well known graphs. Five of these graphs, D¨urer, Franklin, Desargues, Heawood and Tietze can be embedded in the plane, while the remaining graphs, Chv´atal, Goldner-Harrary, Herschel, Fritsch, Gr¨otzsch, Hoffman and Soifer have Euclidean dimension 3. We also present explicit embeddings for all these graphs. 1. History and previous work The Euclidean dimension of a graph G = (V, E), denoted dim(G) is the least integer n such that there exists a 1 : 1 embedding f : V Rn for which f(u) f(v) = 1 if and only → | − | if uv E. ∈ The concept was introduced by Erd˝os, Harary and Tutte in their seminal paper [7], where the authors determine the Euclidean dimension for several classes of graphs. For instance, they show that dim(K ) = n 1, where K is the complete graph on n n − n vertices. Using a construction due to Lenz, they also compute the Euclidean dimension of Km,n, the complete bipartite graph with m vertices in one class and n vertices in the other. -

Operation-Based Notation for Archimedean Graph
Operation-Based Notation for Archimedean Graph Hidetoshi Nonaka Research Group of Mathematical Information Science Division of Computer Science, Hokkaido University N14W9, Sapporo, 060 0814, Japan ABSTRACT Table 1. The list of Archimedean solids, where p, q, r are the number of vertices, edges, and faces, respectively. We introduce three graph operations corresponding to Symbol Name of polyhedron p q r polyhedral operations. By applying these operations, thirteen Archimedean graphs can be generated from Platonic graphs that A(3⋅4)2 Cuboctahedron 12 24 14 are used as seed graphs. A4610⋅⋅ Great Rhombicosidodecahedron 120 180 62 A468⋅⋅ Great Rhombicuboctahedron 48 72 26 Keyword: Archimedean graph, Polyhedral graph, Polyhedron A 2 Icosidodecahedron 30 60 32 notation, Graph operation. (3⋅ 5) A3454⋅⋅⋅ Small Rhombicosidodecahedron 60 120 62 1. INTRODUCTION A3⋅43 Small Rhombicuboctahedron 24 48 26 A34 ⋅4 Snub Cube 24 60 38 Archimedean graph is a simple planar graph isomorphic to the A354 ⋅ Snub Dodecahedron 60 150 92 skeleton or wire-frame of the Archimedean solid. There are A38⋅ 2 Truncated Cube 24 36 14 thirteen Archimedean solids, which are semi-regular polyhedra A3⋅102 Truncated Dodecahedron 60 90 32 and the subset of uniform polyhedra. Seven of them can be A56⋅ 2 Truncated Icosahedron 60 90 32 formed by truncation of Platonic solids, and all of them can be A 2 Truncated Octahedron 24 36 14 formed by polyhedral operations defined as Conway polyhedron 4⋅6 A 2 Truncated Tetrahedron 12 18 8 notation [1-2]. 36⋅ The author has recently developed an interactive modeling system of uniform polyhedra including Platonic solids, Archimedean solids and Kepler-Poinsot solids, based on graph drawing and simulated elasticity, mainly for educational purpose [3-5]. -
![Barnette's Conjecture Arxiv:1310.5504V1 [Math.CO] 21](https://docslib.b-cdn.net/cover/9369/barnettes-conjecture-arxiv-1310-5504v1-math-co-21-2199369.webp)
Barnette's Conjecture Arxiv:1310.5504V1 [Math.CO] 21
Radboud Universiteit Nijmegen Barnette's Conjecture arXiv:1310.5504v1 [math.CO] 21 Oct 2013 Authors: Supervisor: Lean Arts Wieb Bosma Meike Hopman Veerle Timmermans October 22, 2013 Abstract This report provides an overview of theorems and statements related to a conjecture stated by D. W. Barnette in 1969. Barnettes conjecture is an open problem in graph theory about Hamiltonicity of graphs. Conjecture 0.1 (Barnettes conjecture). Every cubic, bipartite, polyhedral graph contains a Hamiltonian cycle. We will have a look Steinitzs theorem, which allows to reformulate the conjecture. We look at the complexity of previous, related, conjectures and determine some necessary conditions for a Barnette graph to contain a Hamiltonian cycle. We will also determine some sufficient conditions for a graph to contain a Hamiltonian cycle. We will give a sketch of the proof for Barnettes conjecture for graphs up to 64 vertices and we will describe two operations by which all Barnette graphs can be constructed. Finally, we will describe some programs in C++ that will help to check some properties in graphs, like bipartiteness, 3-connectedness and Hamiltonicity. Contents 1 Introduction 3 1.1 Preliminaries . .4 2 Steinitz's Theorem 6 3 Tait's Conjecture 9 3.1 Tutte's counterexample . .9 3.2 Smaller counterexamples . 11 3.3 Four color theorem for cubic 3-connected planar graphs . 11 4 Tutte's Conjecture 13 4.1 Horton fragment . 13 4.1.1 Horton-96 . 16 4.1.2 Horton-92 . 17 4.2 Ellingham Fragment . 18 5 Complexity 20 5.1 Tait's conjecture and the necessity of bipartiteness .