Extending Viviani's Theorem to Special Polygons Using Sketchpad
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 and 1991 Bradley C. Klypchak a Dissertation Submitted to the Graduate
PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 AND 1991 Bradley C. Klypchak A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2007 Committee: Dr. Jeffrey A. Brown, Advisor Dr. John Makay Graduate Faculty Representative Dr. Ron E. Shields Dr. Don McQuarie © 2007 Bradley C. Klypchak All Rights Reserved iii ABSTRACT Dr. Jeffrey A. Brown, Advisor Between 1984 and 1991, heavy metal became one of the most publicly popular and commercially successful rock music subgenres. The focus of this dissertation is to explore the following research questions: How did the subculture of heavy metal music between 1984 and 1991 evolve and what meanings can be derived from this ongoing process? How did the contextual circumstances surrounding heavy metal music during this period impact the performative choices exhibited by artists, and from a position of retrospection, what lasting significance does this particular era of heavy metal merit today? A textual analysis of metal- related materials fostered the development of themes relating to the selective choices made and performances enacted by metal artists. These themes were then considered in terms of gender, sexuality, race, and age constructions as well as the ongoing negotiations of the metal artist within multiple performative realms. Occurring at the juncture of art and commerce, heavy metal music is a purposeful construction. Metal musicians made performative choices for serving particular aims, be it fame, wealth, or art. These same individuals worked within a greater system of influence. Metal bands were the contracted employees of record labels whose own corporate aims needed to be recognized. -
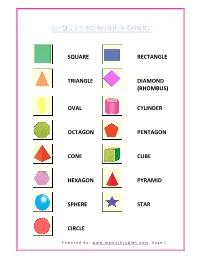
Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface. -

Applying the Polygon Angle
POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°. -

Interior and Exterior Angles of Polygons 2A
Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org G.CO.C.11: Interior and Exterior Angles of Polygons 2a 1 Which type of figure is shown in the accompanying 5 In the diagram below of regular pentagon ABCDE, diagram? EB is drawn. 1) hexagon 2) octagon 3) pentagon 4) quadrilateral What is the measure of ∠AEB? 2 What is the measure of each interior angle of a 1) 36º regular hexagon? 2) 54º 1) 60° 3) 72º 2) 120° 4) 108º 3) 135° 4) 270° 6 What is the measure, in degrees, of each exterior angle of a regular hexagon? 3 Determine, in degrees, the measure of each interior 1) 45 angle of a regular octagon. 2) 60 3) 120 4) 135 4 Determine and state the measure, in degrees, of an interior angle of a regular decagon. 7 A stop sign in the shape of a regular octagon is resting on a brick wall, as shown in the accompanying diagram. What is the measure of angle x? 1) 45° 2) 60° 3) 120° 4) 135° 1 Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org 8 One piece of the birdhouse that Natalie is building 12 The measure of an interior angle of a regular is shaped like a regular pentagon, as shown in the polygon is 120°. How many sides does the polygon accompanying diagram. have? 1) 5 2) 6 3) 3 4) 4 13 Melissa is walking around the outside of a building that is in the shape of a regular polygon. -

Petrie Schemes
Canad. J. Math. Vol. 57 (4), 2005 pp. 844–870 Petrie Schemes Gordon Williams Abstract. Petrie polygons, especially as they arise in the study of regular polytopes and Coxeter groups, have been studied by geometers and group theorists since the early part of the twentieth century. An open question is the determination of which polyhedra possess Petrie polygons that are simple closed curves. The current work explores combinatorial structures in abstract polytopes, called Petrie schemes, that generalize the notion of a Petrie polygon. It is established that all of the regular convex polytopes and honeycombs in Euclidean spaces, as well as all of the Grunbaum–Dress¨ polyhedra, pos- sess Petrie schemes that are not self-intersecting and thus have Petrie polygons that are simple closed curves. Partial results are obtained for several other classes of less symmetric polytopes. 1 Introduction Historically, polyhedra have been conceived of either as closed surfaces (usually topo- logical spheres) made up of planar polygons joined edge to edge or as solids enclosed by such a surface. In recent times, mathematicians have considered polyhedra to be convex polytopes, simplicial spheres, or combinatorial structures such as abstract polytopes or incidence complexes. A Petrie polygon of a polyhedron is a sequence of edges of the polyhedron where any two consecutive elements of the sequence have a vertex and face in common, but no three consecutive edges share a commonface. For the regular polyhedra, the Petrie polygons form the equatorial skew polygons. Petrie polygons may be defined analogously for polytopes as well. Petrie polygons have been very useful in the study of polyhedra and polytopes, especially regular polytopes. -
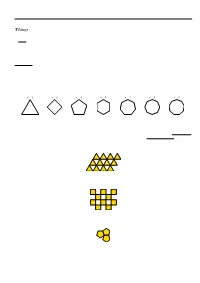
Tilings Page 1
Survey of Math: Chapter 20: Tilings Page 1 Tilings A tiling is a covering of the entire plane with ¯gures which do not not overlap, and leave no gaps. Tilings are also called tesselations, so you will see that word often. The plane is in two dimensions, and that is where we will focus our examination, but you can also tile in one dimension (over a line), in three dimensions (over a space) and mathematically, in even higher dimensions! How cool is that? Monohedral tilings use only one size and shape of tile. Regular Polygons A regular polygon is a ¯gure whose sides are all the same length and interior angles are all the same. n 3 n 4 n 5 n 6 n 7 n 8 n 9 Equilateral Triangle, Square, Pentagon, Hexagon, n-gon for a regular polygon with n sides. Not all of these regular polygons can tile the plane. The regular polygons which do tile the plane create a regular tiling, and if the edge of a tile coincides entirely with the edge of a bordering tile, it is called an edge-to-edge tiling. Triangles have an edge to edge tiling: Squares have an edge to edge tiling: Pentagons don't have an edge to edge tiling: Survey of Math: Chapter 20: Tilings Page 2 Hexagons have an edge to edge tiling: The other n-gons do not have an edge to edge tiling. The problem with the ones that don't (pentagon and n > 6) has to do with the angles in the n-gon. -

Angles of Polygons
5.3 Angles of Polygons How can you fi nd a formula for the sum of STATES the angle measures of any polygon? STANDARDS MA.8.G.2.3 1 ACTIVITY: The Sum of the Angle Measures of a Polygon Work with a partner. Find the sum of the angle measures of each polygon with n sides. a. Sample: Quadrilateral: n = 4 A Draw a line that divides the quadrilateral into two triangles. B Because the sum of the angle F measures of each triangle is 180°, the sum of the angle measures of the quadrilateral is 360°. C D E (A + B + C ) + (D + E + F ) = 180° + 180° = 360° b. Pentagon: n = 5 c. Hexagon: n = 6 d. Heptagon: n = 7 e. Octagon: n = 8 196 Chapter 5 Angles and Similarity 2 ACTIVITY: The Sum of the Angle Measures of a Polygon Work with a partner. a. Use the table to organize your results from Activity 1. Sides, n 345678 Angle Sum, S b. Plot the points in the table in a S coordinate plane. 1080 900 c. Write a linear equation that relates S to n. 720 d. What is the domain of the function? 540 Explain your reasoning. 360 180 e. Use the function to fi nd the sum of 1 2 3 4 5 6 7 8 n the angle measures of a polygon −180 with 10 sides. −360 3 ACTIVITY: The Sum of the Angle Measures of a Polygon Work with a partner. A polygon is convex if the line segment connecting any two vertices lies entirely inside Convex the polygon. -

Pentagon Fuel Use, Climate Change, and the Costs of War
Pentagon Fuel Use, Climate Change, and the Costs of War Neta C. Crawford1 Boston University Updated and Revised, 13 November 20192 Summary If climate change is a “threat multiplier,” as some national security experts and members of the military argue, how does the US military reduce climate change caused threats? Or does war and the preparation for it increase those risks? In its quest for security, the United States spends more on the military than any other country in the world, certainly much more than the combined military spending of its major rivals, Russia and China. Authorized at over $700 billion in Fiscal Year 2019, and with over $700 billion requested for FY2020, the Department of Defense (DOD) budget comprises more than half of all federal discretionary spending each year. With an armed force of more than two million people, 11 nuclear aircraft carriers, and the world’s most advanced military aircraft, the US is more than capable of projecting power anywhere in the globe, and with “Space Command,” into outer space. Further, the US has been continuously at war since late 2001, with the US military and State Department currently engaged in more than 80 countries in counterterror operations.3 All this capacity for and use of military force requires a great deal of energy, most of it in the form of fossil fuel. As General David Petraeus said in 2011, “Energy is the lifeblood of our warfighting capabilities.”4 Although the Pentagon has, in recent years, increasingly 1 Neta C. Crawford is Professor and Chair of Political Science at Boston University, and Co-Director of the Costs of War project at Brown and Boston Universities. -

Three-Dimensional Antipodaland Norm-Equilateral Sets
Pacific Journal of Mathematics THREE-DIMENSIONAL ANTIPODAL AND NORM-EQUILATERAL SETS ACHILL SCHURMANN¨ AND KONRAD J. SWANEPOEL Volume 228 No. 2 December 2006 PACIFIC JOURNAL OF MATHEMATICS Vol. 228, No. 2, 2006 THREE-DIMENSIONAL ANTIPODAL AND NORM-EQUILATERAL SETS ACHILL SCHÜRMANN AND KONRAD J. SWANEPOEL We characterize three-dimensional spaces admitting at least six or at least seven equidistant points. In particular, we show the existence of C∞ norms on ޒ3 admitting six equidistant points, which refutes a conjecture of Lawlor and Morgan (1994, Pacific J. Math. 166, 55–83), and gives the existence of energy-minimizing cones with six regions for certain uniformly convex norms on ޒ3. On the other hand, no differentiable norm on ޒ3 admits seven equidistant points. A crucial ingredient in the proof is a classification of all three-dimensional antipodal sets. We also apply the results to the touching numbers of several three-dimensional convex bodies. 1. Preliminaries Let conv S, int S, bd S denote the convex hull, interior and boundary of a subset S of the n-dimensional real space ޒn. Define A + B := {a + b : a ∈ A, b ∈ B}, λA := {λa : a ∈ A}, A − B := A +(−1)B, x ± A = A ± x := {x}± A. Denote lines and planes by abc and de, triangles and segments by 4abc := conv{a, b, c} and [de] := conv{d, e}, and the Euclidean length of [de] by |de|. Denote the Euclidean inner product by h · , · i.A convex body C ⊂ ޒn is a compact convex set with nonempty interior. The polar of a convex body C is the convex body C∗ := {x ∈ ޒn : hx, yi ≤ 1 for all y ∈ C}. -

Naming Polygons and Interior Angles.Pdf
Naming Polygons & Name ________________________ Problem Set – Interior Angles per __ date ________ Naming polygons: start at a vertex (any vertex) and name that point; then pick a direction and walk around the polygon, naming the points IN ORDER. Example: possible correct names for the heptagon (right) are: heptagon ABCDEFG G heptagon BCDEFGA F heptagon CDEFGAB A heptagon DEFGABC etc. or: E heptagon GFEDCBA heptagon FEDCBAG heptagon EDCBAGF B etc. D C Give ALL POSSIBLE CORRECT names for this quadrilateral. There are 8. 1. quadrilateral __________ 2. quadrilateral __________ X 3. quadrilateral __________ Y 4. quadrilateral __________ 5. quadrilateral __________ 6. quadrilateral __________ W 7. quadrilateral __________ Z 8. quadrilateral __________ Select all of the following CORRECT names (only!) for the polygon below. __ pentagon ABCDE B __ pentagon DBCEA __ pentagon BCDAE C D __ pentagon EADBC __ pentagon CBDEA E __ pentagon DAECB A Naming Polygons & Name ________________________ Problem Set – Interior Angles per __ date ________ Find the value of x. 1. x = _____ 4. x = _____ 10x + 1 3x° 123° (5x – 6)° 137° 104° 91° 12x 2. x = _____ 5. x = _____ (7x – 3)° 133° 10x – 2 93° 8x + 11 12x 5x° 135° 124° 139° 3. x = _____ 6. x = _____ 96° 149° 158° 143° 112° 131° 15x° 9x + 6 12x° 113° 18x° 8x 120° Naming Polygons & Name ________________________ Problem Set – Interior Angles ANSWERS per __ date ________ Naming polygons: start at a vertex (any vertex) and name that point; then pick a direction and walk around the polygon, naming the points IN ORDER. Example: possible correct names for the heptagon (right) are: heptagon ABCDEFG G heptagon BCDEFGA F heptagon CDEFGAB A heptagon DEFGABC etc. -

Areas of Regular Polygons Finding the Area of an Equilateral Triangle
Areas of Regular Polygons Finding the area of an equilateral triangle The area of any triangle with base length b and height h is given by A = ½bh The following formula for equilateral triangles; however, uses ONLY the side length. Area of an equilateral triangle • The area of an equilateral triangle is one fourth the square of the length of the side times 3 s s A = ¼ s2 s A = ¼ s2 Finding the area of an Equilateral Triangle • Find the area of an equilateral triangle with 8 inch sides. Finding the area of an Equilateral Triangle • Find the area of an equilateral triangle with 8 inch sides. 2 A = ¼ s Area3 of an equilateral Triangle A = ¼ 82 Substitute values. A = ¼ • 64 Simplify. A = • 16 Multiply ¼ times 64. A = 16 Simplify. Using a calculator, the area is about 27.7 square inches. • The apothem is the F height of a triangle A between the center and two consecutive vertices H of the polygon. a E G B • As in the activity, you can find the area o any regular n-gon by dividing D C the polygon into congruent triangles. Hexagon ABCDEF with center G, radius GA, and apothem GH A = Area of 1 triangle • # of triangles F A = ( ½ • apothem • side length s) • # H of sides a G B = ½ • apothem • # of sides • side length s E = ½ • apothem • perimeter of a D C polygon Hexagon ABCDEF with center G, This approach can be used to find radius GA, and the area of any regular polygon. apothem GH Theorem: Area of a Regular Polygon • The area of a regular n-gon with side lengths (s) is half the product of the apothem (a) and the perimeter (P), so The number of congruent triangles formed will be A = ½ aP, or A = ½ a • ns. -

Two-Dimensional Figures a Plane Is a Flat Surface That Extends Infinitely in All Directions
NAME CLASS DATE Two-Dimensional Figures A plane is a flat surface that extends infinitely in all directions. A parallelogram like the one below is often used to model a plane, but remember that a plane—unlike a parallelogram—has no boundaries or sides. A plane figure or two-dimensional figure is a figure that lies completely in one plane. When you draw, either by hand or with a computer program, you draw two-dimensional figures. Blueprints are two-dimensional models of real-life objects. Polygons are closed, two-dimensional figures formed by three or more line segments that intersect only at their endpoints. These figures are polygons. These figures are not polygons. This is not a polygon A heart is not a polygon A circle is not a polygon because it is an open because it is has curves. because it is made of figure. a curve. Polygons are named by the number of sides and angles they have. A polygon always has the same number of sides as angles. Listed on the next page are the most common polygons. Each of the polygons shown is a regular polygon. All the angles of a regular polygon have the same measure and all the sides are the same length. SpringBoard® Course 1 Math Skills Workshop 89 Unit 5 • Getting Ready Practice MSW_C1_SE.indb 89 20/07/19 1:05 PM Two-Dimensional Figures (continued) Triangle Quadrilateral Pentagon Hexagon 3 sides; 3 angles 4 sides; 4 angles 5 sides; 5 angles 6 sides; 6 angles Heptagon Octagon Nonagon Decagon 7 sides; 7 angles 8 sides; 8 angles 9 sides; 9 angles 10 sides; 10 angles EXAMPLE A Classify the polygon.