Similarity Measures for Pattern Matching On-The-Fly
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CSS Font Stacks by Classification
CSS font stacks by classification Written by Frode Helland When Johann Gutenberg printed his famous Bible more than 600 years ago, the only typeface available was his own. Since the invention of moveable lead type, throughout most of the 20th century graphic designers and printers have been limited to one – or perhaps only a handful of typefaces – due to costs and availability. Since the birth of desktop publishing and the introduction of the worlds firstWYSIWYG layout program, MacPublisher (1985), the number of typefaces available – literary at our fingertips – has grown exponen- tially. Still, well into the 21st century, web designers find them selves limited to only a handful. Web browsers depend on the users own font files to display text, and since most people don’t have any reason to purchase a typeface, we’re stuck with a selected few. This issue force web designers to rethink their approach: letting go of control, letting the end user resize, restyle, and as the dynamic web evolves, rewrite and perhaps also one day rearrange text and data. As a graphic designer usually working with static printed items, CSS font stacks is very unfamiliar: A list of typefaces were one take over were the previous failed, in- stead of that single specified Stempel Garamond 9/12 pt. that reads so well on matte stock. Am I fighting the evolution? I don’t think so. Some design principles are universal, independent of me- dium. I believe good typography is one of them. The technology that will let us use typefaces online the same way we use them in print is on it’s way, although moving at slow speed. -

Advance Reporting Open Source Licenses 6-67513-02 Rev a August 2012
Advanced Reporting Open-Source Licenses The following table lists the open-source software components used in Quantum Advanced Reporting, as well as the associated licenses. For information on obtaining the Open Source code, contact Quantum Support. (Refer to Getting More Information on page 26 for contact information.) Note: Open source licenses for StorNext® and DXi® products are listed in separate documents, so those licenses are not included in this document. Component Open-Source License AS3 Commons Lang Apache License Version 2.0, January 2004 AS3 Commons Reflect Apache License Version 2.0, January 2004 Cairngorm BSD-style license (BSD Exhibit #2) DejaVu Fonts Bitstream Vera and Arev Font Licenses Image Cropper BSD-style license (BSD Exhibit #3) Libpng BSD 3-Clause, with acknowledgements (BSD Exhibit #1) Perl Licensed under either the Artistic License 2.0 or GNU General Public License version 1 or later. Prototype JS The MIT License rrdtool GNU General Public License, version 2 Scriptaculous The MIT License Spring ActionScript Apache License Version 2.0, January 2004 6-67513-02 Rev A, August 2012 Advance Reporting Open Source Licenses 6-67513-02 Rev A August 2012 Apache License Version 2.0, January 2004 TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION 1. Definitions. “License” shall mean the terms and conditions for use, reproduction, and distribution as defined by Sections 1 through 9 of this document. “Licensor” shall mean the copyright owner or entity authorized by the copyright owner that is granting the License. “Legal Entity” shall mean the union of the acting entity and all other entities that control, are controlled by, or are under common control with that entity. -

P Font-Change Q UV 3
p font•change q UV Version 2015.2 Macros to Change Text & Math fonts in TEX 45 Beautiful Variants 3 Amit Raj Dhawan [email protected] September 2, 2015 This work had been released under Creative Commons Attribution-Share Alike 3.0 Unported License on July 19, 2010. You are free to Share (to copy, distribute and transmit the work) and to Remix (to adapt the work) provided you follow the Attribution and Share Alike guidelines of the licence. For the full licence text, please visit: http://creativecommons.org/licenses/by-sa/3.0/legalcode. 4 When I reach the destination, more than I realize that I have realized the goal, I am occupied with the reminiscences of the journey. It strikes to me again and again, ‘‘Isn’t the journey to the goal the real attainment of the goal?’’ In this way even if I miss goal, I still have attained goal. Contents Introduction .................................................................................. 1 Usage .................................................................................. 1 Example ............................................................................... 3 AMS Symbols .......................................................................... 3 Available Weights ...................................................................... 5 Warning ............................................................................... 5 Charter ....................................................................................... 6 Utopia ....................................................................................... -

Higher Quality 2D Text Rendering
Journal of Computer Graphics Techniques Vol. 2, No. 1, 2013 Higher Quality 2D Text Rendering http://jcgt.org Higher Quality 2D Text Rendering Nicolas P. Rougier INRIA No hinting Native hinting Auto hinting Vertical hinting Figure 1. When displaying text on low-resolution devices (DPI < 150), one typically has to decide if one wants to respect the pixel grid (e.g., Cleartype technology / Microsoft / native hinting) for crisp rendering or, to privilege glyph shapes (Quartz technology / Apple / no hinting) at the cost of blurring. There is, however, a third way that may combine the best of the two technologies (vertical hinting). Abstract Even though text is pervasive in most 3D applications, there is surprisingly no native sup- port for text rendering in OpenGL. To cope with this absence, Mark Kilgard introduced the use of texture fonts [Kilgard 1997]. This technique is well known and widely used and en- sures both good performances and a decent quality in most situations. However, the quality may degrade strongly in orthographic mode (screen space) due to pixelation effects at large sizes and to legibility problems at small sizes due to incorrect hinting and positioning of glyphs. In this paper, we consider font-texture rendering to develop methods to ensure the highest quality in orthographic mode. The method used allows for both the accurate render- ing and positioning of any glyph on the screen. While the method is compatible with complex shaping and/or layout (e.g., the Arabic alphabet), these specific cases are not studied in this article. 50 Journal of Computer Graphics Techniques Vol. -

Please Refer to the Java SE LIUM
Licensing Information User Manual Oracle Java SE 12 Last updated: 2019/02/21 Contents Title and Copyright Information Introduction Licensing Information Description of Product Editions and Permitted Features Prerequisite Products Entitled Products and Restricted Use Licenses Third Party Notices and/or Licenses Title and Copyright Information Introduction This Licensing Information document is a part of the product or program documentation under the terms of your Oracle license agreement and is intended to help you understand the program editions, entitlements, restrictions, prerequisites, special license rights, and/or separately licensed third party technology terms associated with the Oracle software program(s) covered by this document (the “Program(s)”). Entitled or restricted use products or components identified in this document that are not provided with the particular Program may be obtained from the Oracle Software Delivery Cloud website (https://edelivery.oracle.com) or from media Oracle may provide. If you have a question about your license rights and obligations, please contact your Oracle sales representative, review the information provided in Oracle’s Software Investment Guide (http://www.oracle.com/us/corporate/pricing/software-investment-guide/index.html), and/or contact the applicable Oracle License Management Services representative listed on http://www.oracle.com/us/corporate/license-management- services/index.html Licensing Information Description of Product Editions The Java SE products provide the features required to develop, debug, distribute, run, monitor, and manage Java Applications in many different environments, from cloud providers, to servers, to desktops, to constrained devices. Page 1 of 85 The installation packages and features available to each of the products listed below is the same. -

Dell EMC Powerstore Open Source License and Copyright Information
Open Source License and Copyright Information Dell EMC PowerStore Open Source License and Copyright Information June 2021 Rev A04 Revisions Revisions Date Description May 2020 Initial release September 2020 Version updates for some licenses and addition of iwpmd component December 2020 Version updates for some licenses, and addition and deletion of other components January 2021 Version updates for some licenses June 2021 Version updates for some licenses, and addition and deletion of other components The information in this publication is provided “as is.” Dell Inc. makes no representations or warranties of any kind with respect to the information in this publication, and specifically disclaims implied warranties of merchantability or fitness for a particular purpose. Use, copying, and distribution of any software described in this publication requires an applicable software license. Copyright © 2020-2021 Dell Inc. or its subsidiaries. All Rights Reserved. Dell Technologies, Dell, EMC, Dell EMC and other trademarks are trademarks of Dell Inc. or its subsidiaries. Other trademarks may be trademarks of their respective owners. [6/1/2021] [Open Source License and Copyright Information] [Rev A04] 2 Dell EMC PowerStore: Open Source License and Copyright Information Table of contents Table of contents Revisions............................................................................................................................................................................. 2 Table of contents ............................................................................................................................................................... -

Mono Download
Mono download click here to download To access older Mono releases for macOS and Windows, check the archive on the download server. For Linux, please check the "Accessing older releases". Mono runs on Windows, this page describes the various features available for. Mono Basics. Edit page on GitHub. After you get Mono installed, it's probably a. Installing Mono on macOS is very simple : Download the latest Mono release. Download. Release channels: Nightly - Preview - Stable - Visual Studio. This page contains a list of all Mono releases. The latest stable release is. www.doorway.ru repo/ubuntu preview-bionic main" | sudo . Follow the instructions on the download page for the latest stable release. Alternatively, you can also try the preview version. Sponsored by Microsoft, Mono is an open source implementation of Microsoft's. Get Mono. The latest Mono release is waiting for you! Download. Download. The latest MonoDevelop release is: (). Please choose your operating system to view the available packages. Source code is available. First we begin with downloading the installer package, that will install the Run the installer and follow the steps to install Mono's. Download TTF. Z Y M m Download TTF (offsite). Z Y M m Audimat Mono SMeltery 9 Styles. Bitstream Vera Sans Mono font family by Bitstream. Download TTF. Making the web more beautiful, fast, and open through great typography. Plex is an open-source project (OFL) and free to download and use. The Plex family comes in a Sans, Serif, Mono and Sans Condensed, all with roman and true. Mono Framework ; Release Notes. Preview IDE for Visual Studio Visual Studio Tools for Xamarin ; Download for Visual Studio . -

Oss NMC Rel9.Xlsx
Open Source Software Packages for NMC XMP Release 9 Application License Publisher abattis-cantarell-fonts OFL https://git.gnome.org/browse/cantarell-fonts/ abrt GPLv2+ https://abrt.readthedocs.org/ abrt-addon-ccpp GPLv2+ https://abrt.readthedocs.org/ abrt-addon-kerneloops GPLv2+ https://abrt.readthedocs.org/ abrt-addon-pstoreoops GPLv2+ https://abrt.readthedocs.org/ abrt-addon-python GPLv2+ https://abrt.readthedocs.org/ abrt-addon-vmcore GPLv2+ https://abrt.readthedocs.org/ abrt-addon-xorg GPLv2+ https://abrt.readthedocs.org/ abrt-cli GPLv2+ https://abrt.readthedocs.org/ abrt-console-notification GPLv2+ https://abrt.readthedocs.org/ abrt-dbus GPLv2+ https://abrt.readthedocs.org/ abrt-desktop GPLv2+ https://abrt.readthedocs.org/ abrt-gui GPLv2+ https://abrt.readthedocs.org/ abrt-gui-libs GPLv2+ https://abrt.readthedocs.org/ abrt-libs GPLv2+ https://abrt.readthedocs.org/ abrt-python GPLv2+ https://abrt.readthedocs.org/ abrt-retrace-client GPLv2+ https://abrt.readthedocs.org/ abrt-tui GPLv2+ https://abrt.readthedocs.org/ accountsservice GPLv3+ https://www.freedesktop.org/wiki/Software/AccountsService/ accountsservice-libs GPLv3+ https://www.freedesktop.org/wiki/Software/AccountsService/ acl GPLv2+ http://acl.bestbits.at/ adcli LGPLv2+ http://cgit.freedesktop.org/realmd/adcli adwaita-cursor-theme LGPLv3+ or CC-BY-SA http://www.gnome.org adwaita-gtk2-theme LGPLv2+ https://gitlab.gnome.org/GNOME/gnome-themes-extra adwaita-icon-theme LGPLv3+ or CC-BY-SA http://www.gnome.org adwaita-qt5 LGPLv2+ https://github.com/MartinBriza/adwaita-qt aic94xx-firmware -
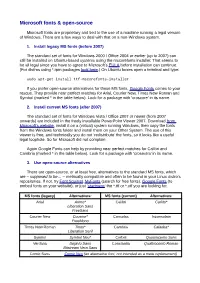
Microsoft Fonts & Open-Source
Microsoft fonts & open-source Microsoft fonts are proprietary and tied to the use of a machine running a legal version of Windows. There are a few ways to deal with that on a non-Windows system. 1. Install legacy MS fonts (before 2007) The standard set of fonts for Windows 2000 / Office 2004 or earlier (up to 2007) can still be installed on Ubuntu-based systems using the mscorefonts installer. That seems to be all legal since you have to agree to Microsoft’s EULA before installation can continue. (For distros using *.rpm packages look here.) On Ubuntu boxes open a terminal and type: sudo apt-get install ttf-mscorefonts-installer If you prefer open-source alternatives for these MS fonts, Google Fonts comes to your rescue. They provide near perfect matches for Arial, Courier New, Times New Roman and Symbol (marked * in the table below). Look for a package with ‘croscore’ in its name. 2. Install current MS fonts (after 2007) The standard set of fonts for Windows Vista / Office 2007 or newer (from 2007 onwards) are included in the freely installable PowerPoint Viewer 2007. Download from Microsoft’s website, install it on a (virtual) system running Windows, then copy the fonts from the Windows fonts folder and install them on your Other System. The use of this viewer is free, and technically you do not ‘redistribute’ the fonts, so it looks like a useful legal loophole. So far Microsoft did not complain. Again Google Fonts can help by providing near perfect matches for Calibri and Cambria (marked * in the table below). -

Azul Zulu 8.53 (8U291-B01) Licensing Information Introduction
Azul Zulu 8.53 (8u291-b01) Licensing Information Introduction Azul Zulu incorporates third-party licensed software packages. Some of these have distribution restrictions and some have only reporting requirements. This document lists the third-party licensed software packages for all Azul Zulu products. In addition to the licenses listed herein, there are numerous copyright notices by individual contributors where the author contributes the code under one of the licenses, with the requirement that the copyright notices be published. These copyright notices are also listed in this document. For portions of the software that are licensed under open source license agreements that require Azul to make the source code available to a licensee, for a period of three years from the date of receipt of Azul Zulu, Azul will provide upon request, a complete machine readable copy of such source code on a medium customarily used for software interchange for a charge no more than the cost of physically performing source distribution. Please email [email protected] for further information. Legal Notices Copyright (c) 2013-2021, Azul Systems, Inc. 385 Moffett Park Drive, Suite 115, Sunnyvale, CA 94089 All rights reserved. Azul Systems, Azul Zulu, and the Azul logo are trademarks or registered trademarks of Azul Systems, Inc. Java and OpenJDK are trademarks or registered trademarks of Oracle and/or its affiliates. All other trademarks are the property of their respective holders and are used here only for identification purposes. Azul Zulu includes copies of the third-party notices required by each module, under a subdirectory with the name of the module in the “legal” subdirectory. -
Download Arial Monospaced Font Free
Download arial monospaced font free click here to download Your font is ready to be downloaded. You are only a step away from downloading your font. We know you are a human but unfortunately our system does not:). Download Arial Monospaced Regular For Free, View Sample Text, Rating And By clicking download and downloading the Font, You agree to our Terms and. Download Arial Monospaced MT Bold For Free, View Sample Text, Rating And By clicking download and downloading the Font, You agree to our Terms and. Download Arial Monospace Regular For Free, View Sample Text, Rating And By clicking download and downloading the Font, You agree to our Terms and. Arial Monospaced® font family, 12 styles from $ by Monotype. Get Arial Monospaced® with the Monotype Library Subscription Try it for free. Pangrams. Arial Monospace Regular Arial Rounded MT Bold Arial Monospace Version 1. 00 ArialMonospace Arial Trademark of Monotype Typography ltd registered in. Thank you for downloading free font Arial Monospace. Arial Monospace. More fonts. Arial Monospace for Windows | Various | views, downloads. Arial Monospaced MT Std Bold font detail page. The world's largest free font site. All the fonts you are looking for here. Available immediately and free download! Download the Arial Monospaced MT Std OpenType Font for free. Fast Downloads. No need to register, just download & install. Arial Monospaced MT / Regular font family. Arial Monospaced MT font characters are listed below. Arial Monospaced MT is a font, manufactured by C) Monotype. Buy Arial Monospaced Regular desktop font from Monotype on www.doorway.ru Arial® Pro Monospaced. Designers: Robin Join for Free Web Fonts; View Family. -
Sh Today Free Font
Sh today free font click here to download At www.doorway.ru, find an amazing collection of thousands of FREE fonts for Windows Today Sans Serif Regular ( downloads) Free For Personal Use. Download, view, test-drive, bookmark free fonts. Features more than free + results for sh today. Related keywords (10) Today SH-Medium Italic. Since the release of these fonts most typefaces in the Scangraphic Type Collection One is designed specifically for headline typesetting (SH. Today SH Medium font by Scangraphic Digital Type Collection, from $ Today SH. — Scangraphic Digital Type Collection Family with 12 Fonts —. 2, th most popular font family of 24, families. Available from MyFonts from. Today Sans Serif SH. Today Sans Now · Today Sans Serif SB · EF Today Sans Serif B · EF Today Sans Serif H · FF Kievit · Metro Office Bold · Metro Office. Download Free sh today Fonts for Windows and Mac. Browse by popularity, category or alphabetical listing. Today à by StereoType. in Script > Old School. 1,, downloads (20 yesterday) 15 comments Free for personal use · Download Donate to. I can't find anything on the TodaySHOP font, but it's on several free font sites (but that doesn't mean it's free ofcourse). The Today SH font is. Buy SG Today Sans Serif SH Bold desktop font from Scangraphic on www.doorway.ru SG Today Sans Serif SH font family - Designed by Volker Küster in Download and install the SH Pinscher free font family by Design Sayshu as well as test-drive and see a complete character set. Font Squirrel is your best resource for FREE, hand-picked, high-quality, commercial-use fonts.