DOCSLIB.ORG

Lecture 7 - Elasticity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 7 - Elasticity Lecture 7 - Elasticity Elasticity Elastic Behavior is the fundamental Stress and Strain in Crystals distinction between solids and liquids •Similartity: both are “condensed matter” Kittel – Ch 3 •A solid or liquid in equilibrium has a definite density (mass per unit volume measured at a given temperature) •The energy increases if the density (volume) is changed from the equilibrium value - e.g. by applying pressure Change of Pressure applied volume to all sides Physics 460 F 2006 Lect 7 1 Physics 460 F 2006 Lect 7 2 Elastic Behavior is the fundamental Strain and Stress distinction between solids and liquids Strain is a change of relative positions of the parts of the material •Difference: •A solid maintains its shape Stress is a force /area applied to the material to cause the strain •The energy increases if the shape is changed – “shear” •A liquid has no preferred shape •It has no resistance to forces that do not change the volume Volume dilation Two types of shear Two types of shear Physics 460 F 2006 Lect 7 3 Physics 460 F 2006 Lect 7 4 Pressure and Bulk Modulus Total Energy of Crystal • Consider first changes in the volume – applies to liquids and any crystal The general shape applies for any type of binding • General approach: E(V) where V is volume Can use ether Ecrystal(Vcrystal) or Ecell(Vcell) since Ecrystal= N Ecell and Vcrystal = N Vcell P = -dE/dV • Pressure = P = - dE/dV (units of Force/Area) = 0 at the minimum Energies of Crystal of Energies • Bulk modulus B = - V dP/dV = V d2E/dV2 (same B = - V dP/dV = V d2E/dV2 units as pressure ) proportional to curvature at the minimum • Compressibility K = 1/B Volume Physics 460 F 2006 Lect 7 5 Physics 460 F 2006 Lect 7 6 1 Lecture 7 - Elasticity Elasticity Elastic Equations • Up to now in the course we considered only • The elastic equations describe the relation of perfect crystals with no external forces stress and strain • Elasticity describes: • Linear relations for small stress/strain • Change in the volume and shape of the crystal when Stress = (elastic constants) x Strain external stresses (force / area) are applied • Sound waves • Large elastic constants fi the material is stiff - a given strain requires a large applied stress • Some aspects of the elastic properties are determined by the symmetry of the crystal • We will give the general relations - but we will consider only cubic crystals • Quantitative values are determined by strength • The same relations apply for isotropic materials like a glass and type of binding of the crystal? • More discussion of general case in Kittel Physics 460 F 2006 Lect 7 7 Physics 460 F 2006 Lect 7 8 Elastic relations in general crystals Elastic Properties of Crystals • Strain and stress are tensors • Definition of strain • Stress eij is force per unit area on a surface Normal n Six independent variables: • Force is a vector F , F , F x y z Force F Using the relation e1 ≡ exx , e2 ≡ eyy , e3 ≡ ezz , • A surface is defined by the exy = eyx etc. e4 ≡ eyz , e5 ≡ exz , e6 ≡ exy normal vector nx, ny, nz • 3 x 3 = 9 quantities • Stress Here Xy denotes force in x direction applied σ1 ≡ σxx = Xx , σ2 ≡ Yy , σ3 ≡ Zz • Strain σij is displacement per unit distance in a to surface normal to y. σ4 ≡ Yz , σ5 ≡ Xz , σ6 ≡ Xy particular direction Displacement u σxy = σyx etc. • Displacement is a vector u , u , u x y z • Linear relation of stress and strain • A position is a vector R , R , R Position R x y z Elastic Constants C • 3 x 3 = 9 quantities ij σi = Σj Cij ej , (i,j = 1,6) -1 ( Also compliances Sij = (C ) ij) Physics 460 F 2006 Lect 7 9 Physics 460 F 2006 Lect 7 10 Strain energy Symmetry Requirements Cubic Crystals • For linear elastic behavior, the energy is quadratic in the strain (or stress) • Simplification in cubic crystals due to symmetry Like Hooke’s law for a spring since x, y, and z are equivalent in cubic crystals • Therefore, the energy is given by: • For cubic crystals all the possible linear elastic information is in 3 quantities: C11 = C11 = C22 = C33 E = (1/2) Σi ei σi = (1/2) Σij ei Cij ej , (i,j = 1,6) C12 = C13 = C23 C = C = C • Valid for all crystals 44 55 66 • Note 21 independent values in general • Note that by symmetry C14 = 0, etc (since Cij = Cji ) • Why is this true for cubic crystals? Physics 460 F 2006 Lect 7 11 Physics 460 F 2006 Lect 7 12 2 Lecture 7 - Elasticity Elasticity in Cubic Crystals Elasticity in Cubic Crystals • Elastic Constants Cij are completely specified by • Elastic Constants Cij are completely specified by 3 values C11 , C12 , C44 3 values C11 , C12 , C44 σ1 = C11 e1 + C12 (e2 + e3) , etc. σ1 = C11 e1 + C12 (e2 + e3) , etc. σ4 = C44 e4 , etc. σ4 = C44 e4 , etc. Pure change in volume – compress equally in x, y, z Two types of shear – no change in volume •For pure dilation δ = ∆V / V e1 = e2 = e3 = δ / 3 C11 -C12 C44 •Define ∆E / V = 1/2 B δ2 No change in volume •Bulk modulus B = (1/3) (C + 2 C ) 11 12 if e2 = e3 = -½ e1 Physics 460 F 2006 Lect 7 13 Physics 460 F 2006 Lect 7 14 Elasticity in Cubic Crystals Elastic Waves • The general form of a displacement pattern is • Pure uniaxial stress and strain ∆r (r ) = u(r ) x + v(r ) y + w(r ) z • σ1 = C11 e1 with e2 = e3 = 0 • A traveling wave is described by 2 ∆r (r ,t) = ∆r exp(ik . r -iωt) • ∆E = (1/2) C11 (δx/x) • Occurs for waves where there is • For simplicity consider waves along the x direction in a no motion in the y or z directions cubic crystal Also for a crystal under Longitudinal waves (motion in x direction) are given by σ1 ≡ Xx stress u(x) = u exp(ikx -iωt) if there are also stresses Transverse waves (motion in y direction) are given by σ2 ≡ Yy , σ3 ≡ Zz of just the right magnitude so that e2 = e3 = 0 v(x) = v exp(ikx -iωt) Physics 460 F 2006 Lect 7 15 Physics 460 F 2006 Lect 7 16 Waves in Cubic Crystals Elastic Waves • Propagation follows from Newton’s Eq. on each volume element ∆V= ∆x ∆y ∆z • Longitudinal waves: ∆y ρ∆V d2 u / dt2 = ∆xdX/ dx = ∆xC d2 u / dx2 x 11 ∆z ∆x y x (note that strain is e1 = d u / dx) •Since ∆V / ∆x = area and ρ area = mass/length = ρL, this leads to z 2 • Variations in x direction ρL u / dt = C11 du/ dx or • Newton’s Eq: ma = F Net force in x direction 2 2 ω = (C11 / ρL ) k • Longitudinal: displacement u along x, 2 2 2 2 • Transverse waves (motion in the y direction) are given ρ∆V d u / dt = ∆xdXx/ dx = ∆xC11 d u / dx by • Transverse: displacement v along y, ω2 = (C / ρ ) k2 2 2 2 2 44 L ρ∆V d v / dt = ∆xdYx/ dx = ∆xC44 d v / dx Physics 460 F 2006 Lect 7 17 Net force in y direction Physics 460 F 2006 Lect 7 18 3 Lecture 7 - Elasticity Sound velocities Young’s Modulus & Poisson Ratio • The relations before give (valid for any elastic wave): • Consider crystal under tension (or compression) in x direction 2 2 ω = (C / ρL ) k or ω = s k • If there are no stresses σ2 ≡ Yy , σ3 ≡ Zz then the crystal will also strain in the y and z directions • where s = sound velocity • Poisson ratio defined by (dy/y) / (dx/x) • Different for longitudinal and transverse waves • Young’s modulus defined by • Longitudinal sound waves can happen in a liquid, gas, Y = tension/ (dx/x) or solid Homework problem • Transverse sound waves exist only in solids to work this out for a cubic crystal y x • More in next chapter on waves Physics 460 F 2006 Lect 7 19 Physics 460 F 2006 Lect 7 20 When does a crystal break? Next Time • Vibrations of atoms in crystals • Consider crystal under tension (or compression) in x direction • Normal modes of harmonic crystal • For large strains, when does it break? • Role of Brillouin Zone • Crystal planes break apart – or slip relative to one another • Quantization and Phonons • Governed by “dislocations” • Read Kittel Ch 4 • See Kittel – Chapter 20 Physics 460 F 2006 Lect 7 21 Physics 460 F 2006 Lect 7 22 4.
Load more

Recommended publications
  • 10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
    EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch.
    [Show full text]
  • Lecture 13: Earth Materials
    Earth Materials Lecture 13 Earth Materials GNH7/GG09/GEOL4002 EARTHQUAKE SEISMOLOGY AND EARTHQUAKE HAZARD Hooke’s law of elasticity Force Extension = E × Area Length Hooke’s law σn = E εn where E is material constant, the Young’s Modulus Units are force/area – N/m2 or Pa Robert Hooke (1635-1703) was a virtuoso scientist contributing to geology, σ = C ε palaeontology, biology as well as mechanics ij ijkl kl ß Constitutive equations These are relationships between forces and deformation in a continuum, which define the material behaviour. GNH7/GG09/GEOL4002 EARTHQUAKE SEISMOLOGY AND EARTHQUAKE HAZARD Shear modulus and bulk modulus Young’s or stiffness modulus: σ n = Eε n Shear or rigidity modulus: σ S = Gε S = µε s Bulk modulus (1/compressibility): Mt Shasta andesite − P = Kεv Can write the bulk modulus in terms of the Lamé parameters λ, µ: K = λ + 2µ/3 and write Hooke’s law as: σ = (λ +2µ) ε GNH7/GG09/GEOL4002 EARTHQUAKE SEISMOLOGY AND EARTHQUAKE HAZARD Young’s Modulus or stiffness modulus Young’s Modulus or stiffness modulus: σ n = Eε n Interatomic force Interatomic distance GNH7/GG09/GEOL4002 EARTHQUAKE SEISMOLOGY AND EARTHQUAKE HAZARD Shear Modulus or rigidity modulus Shear modulus or stiffness modulus: σ s = Gε s Interatomic force Interatomic distance GNH7/GG09/GEOL4002 EARTHQUAKE SEISMOLOGY AND EARTHQUAKE HAZARD Hooke’s Law σij and εkl are second-rank tensors so Cijkl is a fourth-rank tensor. For a general, anisotropic material there are 21 independent elastic moduli. In the isotropic case this tensor reduces to just two independent elastic constants, λ and µ.
    [Show full text]
  • Efficient Hydraulic Fluids Compressibility Is Still One of the Most Critically Important Factors
    WORLDWIDE R. David Whitby Efficient hydraulic fluids Compressibility is still one of the most critically important factors. ydraulic fluids transmit power as a hydraulic system con- while phosphate and vegetable-oil esters have compressibilities H verts mechanical energy into fluid energy and subsequently similar to that of water. Polyalphaolefins are more compressible to mechanical work. To achieve this conversion efficiently, hydrau- than mineral oils. Water-glycol fluids are intermediate between lic fluids need to be relatively incompressible. Hydraulic fluids mineral oils and water. must also minimize wear, reduce friction, provide cooling and pre- Mineral oils are relatively incompressible, but volume reduc- vent rust and corrosion, be compatible with system components tions can be approximately 0.5% for pressures ranging from 6,900 and help keep the system free of deposits. kPa (1,000 psi) up to 27,600 kPa (4,000 psi). Compressibility in- Compressibility measures the rela- creases with pressure and temperature tive change in volume of a fluid or solid and has significant effects on high-pres- as a response to a change in pressure and sure fluid systems. Hydraulic oils typi- is the reciprocal of the volume-elastic cally contain 6% to 10% of dissolved air, modulus or bulk modulus of elasticity. which has no measurable effect on bulk Bulk modulus defines the pressure in- modulus provided it stays in solution. crease needed to cause a given relative Bulk modulus is an inherent property decrease in volume. of the hydraulic fluid and, therefore, is The bulk modulus of a fluid is nonlin- an inherent inefficiency of the hydraulic ear.
    [Show full text]
  • Velocity, Density, Modulus of Hydrocarbon Fluids
    Velocity, Density and Modulus of Hydrocarbon Fluids --Data Measurement De-hua Han*, HARC; M. Batzle, CSM Summary measured with pressure up to 55.2 Mpa (8000 Psi) and temperature up to 100 °C. Density and ultrasonic velocity of numerous hydrocarbon fluids (oil, oil based mud filtrate, hydrocarbon gases and Velocity of Dead Oil miscible CO2-oil) were measured at in situ conditions of pressure up to 50 Mpa and temperatures up to100 °C. Initial measurements were on the gas-free or ‘dead’ oils at Dynamic moduli are derived from velocities and densities. pressure and temperature (see Fig. 1). We used the Newly measured data refine correlations of velocity and following model to fit data: density to API gravity, Gas Oil ratio (GOR), Gas gravity and in situ pressure and temperature. Gas in solution is Vp (m/s) = A – B * T + C * P + D * T * P (1) largely responsible for reducing the bulk modulus of the live oil. Phase changes, such as exsolving gas during Here A is a pseudo velocity at 0 °C and room pressure (0 production, can dramatically lower velocities and modulus, Mpa, gauge), B is temperature gradient, C is pressure but is dependent on pressure conditions. Distinguish gas gradient and D is coefficient of coupled temperature and from liquid phase may not be possible at a high pressure. pressure effects. Fluids are often supercritical. With increasing pressure, a gas-like fluid can begin to behave like a liquid Dead & live oil of #1 B.P. = 1900 psi at 60 C Introduction 1800 1600 Hydrocarbon fluids are the primary targets of the seismic exploration.
    [Show full text]
  • Crack Tip Elements and the J Integral
    EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side.
    [Show full text]
  • FORMULAS for CALCULATING the SPEED of SOUND Revision G
    FORMULAS FOR CALCULATING THE SPEED OF SOUND Revision G By Tom Irvine Email: [email protected] July 13, 2000 Introduction A sound wave is a longitudinal wave, which alternately pushes and pulls the material through which it propagates. The amplitude disturbance is thus parallel to the direction of propagation. Sound waves can propagate through the air, water, Earth, wood, metal rods, stretched strings, and any other physical substance. The purpose of this tutorial is to give formulas for calculating the speed of sound. Separate formulas are derived for a gas, liquid, and solid. General Formula for Fluids and Gases The speed of sound c is given by B c = (1) r o where B is the adiabatic bulk modulus, ro is the equilibrium mass density. Equation (1) is taken from equation (5.13) in Reference 1. The characteristics of the substance determine the appropriate formula for the bulk modulus. Gas or Fluid The bulk modulus is essentially a measure of stress divided by strain. The adiabatic bulk modulus B is defined in terms of hydrostatic pressure P and volume V as DP B = (2) - DV / V Equation (2) is taken from Table 2.1 in Reference 2. 1 An adiabatic process is one in which no energy transfer as heat occurs across the boundaries of the system. An alternate adiabatic bulk modulus equation is given in equation (5.5) in Reference 1. æ ¶P ö B = ro ç ÷ (3) è ¶r ø r o Note that æ ¶P ö P ç ÷ = g (4) è ¶r ø r where g is the ratio of specific heats.
    [Show full text]
  • Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
    Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid
    [Show full text]
  • Chapter 10: Elasticity and Oscillations
    Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2.
    [Show full text]
  • Adiabatic Bulk Moduli
    8.03 at ESG Supplemental Notes Adiabatic Bulk Moduli To find the speed of sound in a gas, or any property of a gas involving elasticity (see the discussion of the Helmholtz oscillator, B&B page 22, or B&B problem 1.6, or French Pages 57-59.), we need the “bulk modulus” of the fluid. This will correspond to the “spring constant” of a spring, and will give the magnitude of the restoring agency (pressure for a gas, force for a spring) in terms of the change in physical dimension (volume for a gas, length for a spring). It turns out to be more useful to use an intensive quantity for the bulk modulus of a gas, so what we want is the change in pressure per fractional change in volume, so the bulk modulus, denoted as κ (the Greek “kappa” which, when written, has a great tendency to look like k, and in fact French uses “K”), is ∆p dp κ = − , or κ = −V . ∆V/V dV The minus sign indicates that for normal fluids (not all are!), a negative change in volume results in an increase in pressure. To find the bulk modulus, we need to know something about the gas and how it behaves. For our purposes, we will need three basic principles (actually 2 1/2) which we get from thermodynamics, or the kinetic theory of gasses. You might well have encountered these in previous classes, such as chemistry. A) The ideal gas law; pV = nRT , with the standard terminology. B) The first law of thermodynamics; dU = dQ − pdV,whereUis internal energy and Q is heat.
    [Show full text]
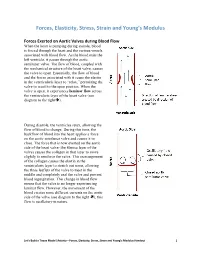
  • Forces, Elasticity, Stress, Strain and Young's Modulus Handout
    Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature.
    [Show full text]
  • Course: US01CPHY01 UNIT – 1 ELASTICITY – I Introduction
    Course: US01CPHY01 UNIT – 1 ELASTICITY – I Introduction: If the distance between any two points in a body remains invariable, the body is said to be a rigid body. In practice it is not possible to have a perfectly rigid body. The deformations are (i) There may be change in length (ii) There is a change of volume but no change in shape (iii) There is a change in shape with no change in volume All bodies get deformed under the action of force. The size and shape of the body will change on application of force. There is a tendency of body to recover its original size and shape on removal of this force. Elasticity: The property of a material body to regain its original condition on the removal of deforming forces, is called elasticity. Quartz fibre is considered to be the perfectly elastic body. Plasticity: The bodies which do not show any tendency to recover their original condition on the removal of deforming forces are called plasticity. Putty is considered to be the perfectly plastic body. Load: The load is the combination of external forces acting on a body and its effect is to change the form or the dimensions of the body. Any kind of deforming force is known as Load. When a body is subjected to a force or a system of forces it undergoes a change in size or shape or both. Elastic bodies offer appreciable resistance to the deforming forces. As a result, work has to be done to deform them. This amount of work is stored in body as elastic potential energy.
    [Show full text]
  • The Mechanical Properties and Elastic Anisotropies of Cubic Ni3al from First Principles Calculations
    crystals Article The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations Xinghe Luan 1,2, Hongbo Qin 1,2,* ID , Fengmei Liu 1,*, Zongbei Dai 1, Yaoyong Yi 1 and Qi Li 1 1 Guangdong Provincial Key Laboratory of Advanced Welding Technology, Guangdong Welding Institute (China-Ukraine E.O. Paton Institute of Welding), Guangzhou 541630, China; [email protected] (X.L.); [email protected] (Z.D.); [email protected] (Y.Y.); [email protected] (Q.L.) 2 Key Laboratory of Guangxi Manufacturing System and Advanced Manufacturing Technology, Guilin University of Electronic Technology, Guilin 541004, China * Correspondence: [email protected] (H.Q.); [email protected] (F.L.) Received: 21 June 2018; Accepted: 22 July 2018; Published: 25 July 2018 Abstract: Ni3Al-based superalloys have excellent mechanical properties which have been widely used in civilian and military fields. In this study, the mechanical properties of the face-centred cubic structure Ni3Al were investigated by a first principles study based on density functional theory (DFT), and the generalized gradient approximation (GGA) was used as the exchange-correlation function. The bulk modulus, Young’s modulus, shear modulus and Poisson’s ratio of Ni3Al polycrystal were calculated by Voigt-Reuss approximation method, which are in good agreement with the existing experimental values. Moreover, directional dependences of bulk modulus, Young’s modulus, shear modulus and Poisson’s ratio of Ni3Al single crystal were explored. In addition, the thermodynamic properties (e.g., Debye temperature) of Ni3Al were investigated based on the calculated elastic constants, indicating an improved accuracy in this study, verified with a small deviation from the previous experimental value.
    [Show full text]