Hop-By-Hop Routing Algorithms for Premium Traffic ∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TCP Over Wireless Multi-Hop Protocols: Simulation and Experiments
TCP over Wireless Multi-hop Protocols: Simulation and Experiments Mario Gerla, Rajive Bagrodia, Lixia Zhang, Ken Tang, Lan Wang {gerla, rajive, lixia, ktang, lanw}@cs.ucla.edu Wireless Adaptive Mobility Laboratory Computer Science Department University of California, Los Angeles Los Angeles, CA 90095 http://www.cs.ucla.edu/NRL/wireless Abstract include mobility, unpredictable wireless channel such as fading, interference and obstacles, broadcast medium shared In this study we investigate the interaction between TCP and by multiple users and very large number of heterogeneous MAC layer in a wireless multi-hop network. This type of nodes (e.g., thousands of sensors). network has traditionally found applications in the military To these challenging physical characteristics of the ad-hoc (automated battlefield), law enforcement (search and rescue) network, we must add the extremely demanding requirements and disaster recovery (flood, earthquake), where there is no posed on the network by the typical applications. These fixed wired infrastructure. More recently, wireless "ad-hoc" include multimedia support, multicast and multi-hop multi-hop networks have been proposed for nomadic computing communications. Multimedia (voice, video and image) is a applications. Key requirements in all the above applications are reliable data transfer and congestion control, features that are must when several individuals are collaborating in critical generally supported by TCP. Unfortunately, TCP performs on applications with real time constraints. Multicasting is a wireless in a much less predictable way than on wired protocols. natural extension of the multimedia requirement. Multi- Using simulation, we provide new insight into two critical hopping is justified (among other things) by the limited problems of TCP over wireless multi-hop. -

Configuring Ipv6 First Hop Security
Configuring IPv6 First Hop Security This chapter describes how to configure First Hop Security (FHS) features on Cisco NX-OS devices. This chapter includes the following sections: • About First-Hop Security, on page 1 • About vPC First-Hop Security Configuration, on page 3 • RA Guard, on page 6 • DHCPv6 Guard, on page 7 • IPv6 Snooping, on page 8 • How to Configure IPv6 FHS, on page 9 • Configuration Examples, on page 17 • Additional References for IPv6 First-Hop Security, on page 18 About First-Hop Security The Layer 2 and Layer 3 switches operate in the Layer 2 domains with technologies such as server virtualization, Overlay Transport Virtualization (OTV), and Layer 2 mobility. These devices are sometimes referred to as "first hops", specifically when they are facing end nodes. The First-Hop Security feature provides end node protection and optimizes link operations on IPv6 or dual-stack networks. First-Hop Security (FHS) is a set of features to optimize IPv6 link operation, and help with scale in large L2 domains. These features provide protection from a wide host of rogue or mis-configured users. You can use extended FHS features for different deployment scenarios, or attack vectors. The following FHS features are supported: • IPv6 RA Guard • DHCPv6 Guard • IPv6 Snooping Note See Guidelines and Limitations of First-Hop Security, on page 2 for information about enabling this feature. Configuring IPv6 First Hop Security 1 Configuring IPv6 First Hop Security IPv6 Global Policies Note Use the feature dhcp command to enable the FHS features on a switch. IPv6 Global Policies IPv6 global policies provide storage and access policy database services. -

Junos® OS Protocol-Independent Routing Properties User Guide Copyright © 2021 Juniper Networks, Inc
Junos® OS Protocol-Independent Routing Properties User Guide Published 2021-09-22 ii Juniper Networks, Inc. 1133 Innovation Way Sunnyvale, California 94089 USA 408-745-2000 www.juniper.net Juniper Networks, the Juniper Networks logo, Juniper, and Junos are registered trademarks of Juniper Networks, Inc. in the United States and other countries. All other trademarks, service marks, registered marks, or registered service marks are the property of their respective owners. Juniper Networks assumes no responsibility for any inaccuracies in this document. Juniper Networks reserves the right to change, modify, transfer, or otherwise revise this publication without notice. Junos® OS Protocol-Independent Routing Properties User Guide Copyright © 2021 Juniper Networks, Inc. All rights reserved. The information in this document is current as of the date on the title page. YEAR 2000 NOTICE Juniper Networks hardware and software products are Year 2000 compliant. Junos OS has no known time-related limitations through the year 2038. However, the NTP application is known to have some difficulty in the year 2036. END USER LICENSE AGREEMENT The Juniper Networks product that is the subject of this technical documentation consists of (or is intended for use with) Juniper Networks software. Use of such software is subject to the terms and conditions of the End User License Agreement ("EULA") posted at https://support.juniper.net/support/eula/. By downloading, installing or using such software, you agree to the terms and conditions of that EULA. iii Table -

Don't Trust Traceroute (Completely)
Don’t Trust Traceroute (Completely) Pietro Marchetta, Valerio Persico, Ethan Katz-Bassett Antonio Pescapé University of Southern California, CA, USA University of Napoli Federico II, Italy [email protected] {pietro.marchetta,valerio.persico,pescape}@unina.it ABSTRACT In this work, we propose a methodology based on the alias resolu- tion process to demonstrate that the IP level view of the route pro- vided by traceroute may be a poor representation of the real router- level route followed by the traffic. More precisely, we show how the traceroute output can lead one to (i) inaccurately reconstruct the route by overestimating the load balancers along the paths toward the destination and (ii) erroneously infer routing changes. Categories and Subject Descriptors C.2.1 [Computer-communication networks]: Network Architec- ture and Design—Network topology (a) Traceroute reports two addresses at the 8-th hop. The common interpretation is that the 7-th hop is splitting the traffic along two Keywords different forwarding paths (case 1); another explanation is that the 8- th hop is an RFC compliant router using multiple interfaces to reply Internet topology; Traceroute; IP alias resolution; IP to Router to the source (case 2). mapping 1 1. INTRODUCTION 0.8 Operators and researchers rely on traceroute to measure routes and they assume that, if traceroute returns different IPs at a given 0.6 hop, it indicates different paths. However, this is not always the case. Although state-of-the-art implementations of traceroute al- 0.4 low to trace all the paths -

Routing Loop Attacks Using Ipv6 Tunnels
Routing Loop Attacks using IPv6 Tunnels Gabi Nakibly Michael Arov National EW Research & Simulation Center Rafael – Advanced Defense Systems Haifa, Israel {gabin,marov}@rafael.co.il Abstract—IPv6 is the future network layer protocol for A tunnel in which the end points’ routing tables need the Internet. Since it is not compatible with its prede- to be explicitly configured is called a configured tunnel. cessor, some interoperability mechanisms were designed. Tunnels of this type do not scale well, since every end An important category of these mechanisms is automatic tunnels, which enable IPv6 communication over an IPv4 point must be reconfigured as peers join or leave the tun- network without prior configuration. This category includes nel. To alleviate this scalability problem, another type of ISATAP, 6to4 and Teredo. We present a novel class of tunnels was introduced – automatic tunnels. In automatic attacks that exploit vulnerabilities in these tunnels. These tunnels the egress entity’s IPv4 address is computationally attacks take advantage of inconsistencies between a tunnel’s derived from the destination IPv6 address. This feature overlay IPv6 routing state and the native IPv6 routing state. The attacks form routing loops which can be abused as a eliminates the need to keep an explicit routing table at vehicle for traffic amplification to facilitate DoS attacks. the tunnel’s end points. In particular, the end points do We exhibit five attacks of this class. One of the presented not have to be updated as peers join and leave the tunnel. attacks can DoS a Teredo server using a single packet. The In fact, the end points of an automatic tunnel do not exploited vulnerabilities are embedded in the design of the know which other end points are currently part of the tunnels; hence any implementation of these tunnels may be vulnerable. -

Are We One Hop Away from a Better Internet?
Are We One Hop Away from a Better Internet? Yi-Ching Chiu,∗ Brandon Schlinker,∗ Abhishek Balaji Radhakrishnan, Ethan Katz-Bassett, Ramesh Govindan Department of Computer Science, University of Southern California ABSTRACT of networks. A second challenge is that the goal is often an approach The Internet suffers from well-known performance, reliability, and that works in the general case, applicable equally to any Internet security problems. However, proposed improvements have seen lit- path, and it may be difficult to design such general solutions. tle adoption due to the difficulties of Internet-wide deployment. We We argue that, instead of solving problems for arbitrary paths, we observe that, instead of trying to solve these problems in the general can think in terms of solving problems for an arbitrary byte, query, case, it may be possible to make substantial progress by focusing or dollar, thereby putting more focus on paths that carry a higher on solutions tailored to the paths between popular content providers volume of traffic. Most traffic concentrates along a small number and their clients, which carry a large share of Internet traffic. of routes due to a number of trends: the rise of Internet video In this paper, we identify one property of these paths that may had led to Netflix and YouTube alone accounting for nearly half provide a foothold for deployable solutions: they are often very short. of North American traffic [2], more services are moving to shared Our measurements show that Google connects directly to networks cloud infrastructure, and a small number of mobile and broadband hosting more than 60% of end-user prefixes, and that other large providers deliver Internet connectivity to end-users. -

Reverse Traceroute
Reverse Traceroute Ethan Katz-Bassett, Harsha V. Madhyastha, Vijay K. Adhikari, Colin Scott, Justine Sherry, Peter van Wesep, Arvind Krishnamurthy, Thomas Anderson NSDI, April 2010 This work partially supported by Cisco, Google, NSF Researchers Need Reverse Paths, Too The inability to measure reverse paths was the biggest limitation of my previous systems: ! Geolocation constraints too loose [IMC ‘06] ! Hubble can’t locate reverse path outages [NSDI ‘08] ! iPlane predictions inaccurate [NSDI ‘09] Other systems use sophisticated measurements but are forced to assume symmetric paths: ! Netdiff compares ISP performance [NSDI ‘08] ! iSpy detects prefix hijacking [SIGCOMM ‘08] ! Eriksson et al. infer topology [SIGCOMM ʻ08] Everyone Needs Reverse Paths “The number one go-to tool is traceroute. Asymmetric paths are the number one plague. The reverse path itself is completely invisible.” NANOG Network operators troubleshooting tutorial, 2009. Goal: Reverse traceroute, without control of destination and deployable today without new support ! Want path from D back to S, don’t control D ! Traceroute gives S to D, but likely asymmetric ! Can’t use traceroute’s TTL limiting on reverse path KEY IDEA ! Technique does not require control of destination ! Want path from D back to S, don’t control D ! Set of vantage points KEY IDEA ! Multiple VPs combine for view unattainable from any one ! Traceroute from all vantage points to S ! Gives atlas of paths to S; if we hit one, we know rest of path " Destination-based routing KEY IDEA ! Traceroute atlas gives -

Improving the Reliability of Internet Paths with One-Hop Source Routing
Improving the Reliability of Internet Paths with One-hop Source Routing Krishna P. Gummadi, Harsha V. Madhyastha, Steven D. Gribble, Henry M. Levy, and David Wetherall Department of Computer Science & Engineering University of Washington {gummadi, harsha, gribble, levy, djw}@cs.washington.edu Abstract 1 Introduction Internet reliability demands continue to escalate as the Recent work has focused on increasing availability Internet evolves to support applications such as banking in the face of Internet path failures. To date, pro- and telephony. Yet studies over the past decade have posed solutions have relied on complex routing and path- consistently shown that the reliability of Internet paths monitoring schemes, trading scalability for availability falls far short of the “five 9s” (99.999%) of availability among a relatively small set of hosts. expected in the public-switched telephone network [11]. This paper proposes a simple, scalable approach to re- Small-scale studies performed in 1994 and 2000 found cover from Internet path failures. Our contributions are the chance of encountering a major routing pathology threefold. First, we conduct a broad measurement study along a path to be 1.5% to 3.3% [17, 26]. of Internet path failures on a collection of 3,153 Internet Previous research has attempted to improve Internet destinations consisting of popular Web servers, broad- reliability by various means, including server replica- band hosts, and randomly selected nodes. We monitored tion, multi-homing, or overlay networks. While effec- these destinations from 67 PlanetLab vantage points over tive, each of these techniques has limitations. For ex- a period of seven days, and found availabilities ranging ample, replication through clustering or content-delivery from 99.6% for servers to 94.4% for broadband hosts. -

RIP: Routing Information Protocol a Routing Protocol Based on the Distance-Vector Algorithm
Laboratory 6 RIP: Routing Information Protocol A Routing Protocol Based on the Distance-Vector Algorithm Objective The objective of this lab is to configure and analyze the performance of the Routing Information Protocol (RIP) model. Overview A router in the network needs to be able to look at a packet’s destination address and then determine which of the output ports is the best choice to get the packet to that address. The router makes this decision by consulting a forwarding table. The fundamental problem of routing is: How do routers acquire the information in their forwarding tables? Routing algorithms are required to build the routing tables and hence forwarding tables. The basic problem of routing is to find the lowest-cost path between any two nodes, where the cost of a path equals the sum of the costs of all the edges that make up the path. Routing is achieved in most practical networks by running routing protocols among the nodes. The protocols provide a distributed, dynamic way to solve the problem of finding the lowest-cost path in the presence of link and node failures and changing edge costs. One of the main classes of routing algorithms is the distance-vector algorithm. Each node constructs a vector containing the distances (costs) to all other nodes and distributes that vector to its immediate neighbors. RIP is the canonical example of a routing protocol built on the distance-vector algorithm. Routers running RIP send their advertisements regularly (e.g., every 30 seconds). A router also sends an update message whenever a triggered update from another router causes it to change its routing table. -

Lab 2.8.1: Basic Static Route Configuration
Lab 2.8.1: Basic Static Route Configuration Topology Diagram Addressing Table Device Interface IP Address Subnet Mask Default Gateway Fa0/0 172.16.3.1 255.255.255.0 N/A R1 S0/0/0 172.16.2.1 255.255.255.0 N/A Fa0/0 172.16.1.1 255.255.255.0 N/A R2 S0/0/0 172.16.2.2 255.255.255.0 N/A S0/0/1 192.168.1.2 255.255.255.0 N/A FA0/0 192.168.2.1 255.255.255.0 N/A R3 S0/0/1 192.168.1.1 255.255.255.0 N/A PC1 NIC 172.16.3.10 255.255.255.0 172.16.3.1 PC2 NIC 172.16.1.10 255.255.255.0 172.16.1.1 PC3 NIC 192.168.2.10 255.255.255.0 192.168.2.1 Learning Objectives Upon completion of this lab, you will be able to: • Cable a network according to the Topology Diagram. • Erase the startup configuration and reload a router to the default state. • Perform basic configuration tasks on a router. All contents are Copyright © 1992–2007 Cisco Systems, Inc. All rights reserved. This document is Cisco Public Information. Page 1 of 20 CCNA Exploration Routing Protocols and Concepts: Static Routing Lab 2.8.1: Basic Static Route Configuration • Interpret debug ip routing output. • Configure and activate Serial and Ethernet interfaces. • Test connectivity. • Gather information to discover causes for lack of connectivity between devices. • Configure a static route using an intermediate address. -
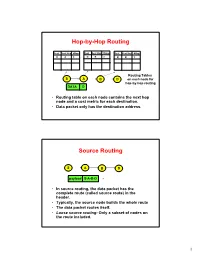
Hop-By-Hop Routing Source Routing
Hop-by-Hop Routing Dest. Next Hop #Hops Dest. Next Hop #Hops Dest. Next Hop #Hops D A 3 D B 2 D D 1 Routing Tables S A B D on each node for hop-by-hop routing DATA D • Routing table on each node contains the next hop node and a cost metric for each destination. • Data packet only has the destination address. Source Routing S A B D payload S-A-B-D • In source routing, the data packet has the complete route (called source route) in the header. • Typically, the source node builds the whole route • The data packet routes itself. • Loose source routing: Only a subset of nodes on the route included. 1 Static vs. Dynamic Routing • Static routing has fixed routes, set up by network administrators, for example. • Dynamic routing is network state- dependent. Routes may change dynamically depending on the “state” of the network. • State = link costs. Switch traffic from highly loaded links to less loaded links. Distributed, Dynamic Routing Protocols • Distributed because in a dynamic network, no single, centralized node “knows” the whole “state” of the network. • Dynamic because routing must respond to “state” changes in the network for efficiency. • Two class of protocols: Link State and Distance Vector. 2 Link State Protocol • Each node “floods” the network with link state packets (LSP) describing the cost of its own (outgoing) links. – Link cost metric = typically delay for traversing the link. – Every other node in the network gets the LSPs via the flooding mechanism. • Each node maintains a LSP database of all LSPs it received. -

Hop Count in the Internet
MEASUREMENTS OF THE HOPCOUNT IN INTERNET Measurements of the Hopcount in Internet F. Begtaševiü and P. Van Mieghem End-to-end quality of service is likely to depend traceroute utility among 37 Internet sites. His on the hopcount, the number of traversed goal was to study the routing behavior routers. In this paper we present the results of including pathologies, stability and path the measurements of the hopcount from a source symmetry. His data showed that the paths for at Delft towards several destinations spread over most of the sites (almost two-thirds) stayed the three continents. Fitting the data with our same over longer period of time. About half of theoretical model illustrates that the number of routers based on our measurements is estimated the paths were asymmetric. at around 105. The changes in the hopcount over Vanhastel et al [7] published their results of time are investigated. It was found that though the measurements performed at the University there is virtually no short-term change in the of Gent in 1998, but the number of destination average hopcount the individual hopcounts do sites they used is rather small. Moreover, they change significantly. Rapid changes in the paths did not study the changes in the hopcount nor were observed to barely affect the hopcount. in that of the paths. PingER is a large end-to-end performance monitoring project [4], organized by the I. INTRODUCTION researchers from different institutes working In order to understand the current behavior of on High Energy Physics experiments the Internet better, the properties of qualifiers (HEPnet).