Reappraisal of Hydrological Studies for Computation of Dependable Flows
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(EC) (14.03.2018) Accorded for Expansion of Gondegaon Extension OC, Nagpur Area, Dt
Compliance Report for Amendment in Environmental Clearance (EC) (14.03.2018) Accorded for Expansion of Gondegaon Extension OC, Nagpur Area, Dt. Nagpur Maharashtra. June 2018 Western Coalfields Limited Nagpur 1 Expansion of Gondegaon Extension OC Sub:- Extension in validity of EC accorded for Expansion of Gondegaon Extension OC Coal mine Project from 2.5 MTPA to 3.5 MTPA of Western Coalfields Limited within existing ML area of 917 Ha located in Gondegaon Village, Parseoni Tehsil, Nagpur District, Maharashtra under Clause 7(ii) of the EIA Notification, 2006 – Amendment reg. Ref:- 1. EC letter accorded by MoEF & CC vide letter no. J-11015/106/2009 - IA.II(M) dated 14-03-2018. 1.0 Background: The proposal for Expansion of Gondegaon Extension OC Coal mine Project from 2.5 MTPA to 3.5 MTPA by M/s. Western Coalfields Limited in an area of 917 ha located in village Gondegaon, Tehsil Parseoni, District Nagpur was submitted through online portal of MoEF & CC vide no. IA/MH/CMIN/71601/2017 dated 14-12-2017. Subsequently, the proposal was considered by the EAC (TP & C) in its 24th meeting held on 11-01-2018. Based on the recommendation of the EAC, MoEF & CC accorded EC for the subject project vide letter J-11015/106/2009-IA.II(M) dated 14-03-2018 for enhancement in production capacity from 2.5 MTPA to 3.5 MTPA in a total area of 917 ha (mine lease area 845.74 ha) for a period of one year subject to compliance of terms and conditions and environmental safeguards mentioned below: i. -

GRMB Annual Report 2017-18
Government of India Ministry of Water Resources, RD & GR Godavari River Management Board ANNUAL REPORT 2017-18 GODAVARI BASIN – Dakshina Ganga Origin Brahmagiri near Trimbakeshwar, Nasik Dist., Maharashtra Geographical Area 9.50 % of Total GA of India Area & Location Latitude - 16°19’ to 22°34’ North Longitude – 73°24’ to 83° 4’ East Boundaries West: Western Ghats North: Satmala hills, the Ajanta range and the Mahadeo hills East: Eastern Ghats & the Bay of Bengal South: Balaghat & Mahadeo ranges stretching forth from eastern flank of the Western Ghats & the Anantgiri and other ranges of the hills and ridges separate the Gadavari basin from the Krishna basin. Catchment Area 3,12,812 Sq.km Length of the River 1465 km States Maharashtra (48.6%), Telangana (18.8%), Andhra Pradesh (4.5%), Chhattisgarh (10.9%), Madhya Pradesh (10.0%), Odisha (5.7%), Karnataka (1.4%) and Puducherry (Yanam) and emptying into Bay of Bengal Length in AP & TS 772 km Major Tributaries Pravara, Manjira, Manair – Right side of River Purna, Pranhita, Indravati, Sabari – Left side of River Sub- basins Twelve (G1- G12) Dams Gangapur Dam, Jayakwadi dam, Vishnupuri barrage, Ghatghar Dam, Upper Vaitarna reservoir, Sriram Sagar Dam, Dowleswaram Barrage. Hydro power stations Upper Indravati 600 MW Machkund 120 MW Balimela 510 MW Upper Sileru 240 MW Lower Sileru 460 MW Upper Kolab 320 MW Pench 160 MW Ghatghar pumped storage 250 MW Polavaram (under 960 MW construction) ANNUAL REPORT 2017-18 GODAVARI RIVER MANAGEMENT BOARD 5th Floor, Jalasoudha, Errum Manzil, Hyderabad- 500082 FROM CHAIRMAN’S DESK It gives me immense pleasure to present the Annual Report of Godavari River Management Board (GRMB) for the year 2017-18. -
MGL-INT-1-2016-UNPAID SHAREHOLDERS LIST AS 30-06-2021.Xlsx
FOLIO-DEMAT ID DWNO NETDIV NAME ADDRESS 1 ADDRESS 2 ADDRESS 3 City PIN 1203280000222453 16110214 23.00 BENOY CHERIAN . P O BOX 10315 DANWAY QATAR DOHA 0 IN30167010076943 16111106 45.00 SHARANJIT KAUR E - 205 AMAR COLONY LAJPAT NAGAR - IV NEW DELHI 110024 IN30226913012127 16112294 7.00 ABHISHEK ATTRI FLAT NO 78 POCKET 4 BLOCK D SECTOR 15 ROHINI DELHI DELHI INDIA 110085 1204470006200258 16112337 9.00 SATYAPAL SINGH D-1/6A PHASE-1 BLOCK D-1 BUDDH VIHAR DELHI 110086 IN30177416845663 16114732 45.00 POOJA SINGHAL H NO 349 STRT MAMOORA GANV VILL MAMOORA POLICE STN SEC 58 GAUTAM BUDH NAGAR NOIDA 201307 IN30105510700089 16114941 118.00 DAYA SHANKER SHUKLA 10/175 KHALASI LINE KANPUR 208002 1202060000069367 16110595 45.00 INDERA DEVI 7232 ROOP NAGAR NEW DELHI 110007 1204470005506787 16111071 9.00 PANKAJ SETHI A-I-136 LAJPAT NAGAR I DELHI 110024 1204470001327271 16111440 11.00 ANUPAMA GUPTA 145/5 FRIENDS ENCLAVE S P ROAD NANGLOI DELHI 110041 IN30131320232745 16111627 39.00 PAWAN KUMAR JAIN 172 WEST AZAD NAGAR OPP EVERGREEN PUBLIC SCHOOL KRISHNA NAGAR DELHI 110051 1204470002696978 16111937 5.00 BALJIT SINGH 25 - B HARI NAGAR DELHI DELHI 110064 IN30223610816408 16112288 900.00 MANORANJAN SOOD 81 NAVYUG APARTMENTS SECTOR 9 ROHINI DELHI 110085 IN30223610157507 16110526 45.00 RAJEEV SETHI 14 A/3 W E A KAROL BAGH NEW DELHI 110005 1204470002710628 16110557 11.00 SHEHZAD AHMAD 3592 MAIN ROAD BARA HINDU RAO DELHI 110006 1203320007146634 16110882 270.00 MOHINDER KAUR B-162 I FLOOR FATEH NAGAR DELHI 110018 IN30311610826815 16111208 40.00 VIDHI NARANG J -101 -
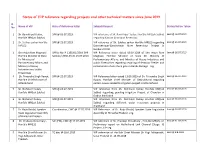
Status of VIP Reference Regarding Projects and Other Technical Matters Since June 2019
Status of VIP reference regarding projects and other technical matters since June 2019 Sl. No Name of VIP Date of Reference letter Subject/Request Status/Action Taken No 1 Sh. Ram Kripal Yadav, SPR @ 03.07.2019 VIP reference of Sh. Ram Kripal Yadav, Hon'ble MP(Lok Sabha) Sent @ 16.07.2019 Hon'ble MP(Lok Sabha) regarding Kadvan (Indrapuri Reservior) 2 Sh. Subhas sarkar Hon'ble SPR @ 23.07.2019 VIP reference of Sh. Subhas sarkar Hon'ble MP(LS) regarding Sent @ 25.07.2019 MP(LS) Dwrakeshwar-Gandheswar River Reserviour Project in Bankura (W.B) 3 Shri Arjun Ram Meghwal SPR Lr.No. P-11019/1/2019-SPR VIP Reference letter dated 09.07.2019 of Shri Arjun Ram Sent @ 26.07.2019 Hon’ble Minister of State Section/ 2900-03 dt. 25.07.2019 Meghwal Hon’ble Minister of State for Ministry of for Ministry of Parliamentary Affairs; and Ministry of Heavy Industries and Parliamentary Affairs; and public Enterprises regarding repairing of ferozpur Feeder and Ministry of Heavy construction of one more gate in Harike Barrage -reg Industries and public Enterprises 4 Sh. Trivendra Singh Rawat, SPR @ 22.07.2019 VIP Reference letter dated 13.06.2019 of Sh. Trivendra Singh Sent @ 26.07.2019 Hon’ble Chief Minister of Rawat, Hon’ble Chief Minister of Uttarakhand regarding Uttarakhand certain issues related to irrigation project in Uttarakhand. 5 Sh. Nishikant Dubey SPR @ 03.07.2019 VIP reference from Sh. Nishikant Dubey Hon'ble MP(Lok Sent @ 26.07.2019 Hon'ble MP(Lok Sabha) Sabha) regarding pending Irrigation Project of Chandan in Godda Jharkhand 6 Sh. -

Maharashtra 211Th Meeting of SEIAA (VC2
State Environment Impact Assessment Authority (SEIAA) Maharashtra 211th Meeting of SEIAA (VC2)(PART-4) AGENDA Venue: Meeting Through Video Conferencing Please Check MoEF&CC Website at www.parivesh.nic.in for details and updates Date : 08 Dec 2020 Time : 12.00 PM Onwards CONSIDERATION/RECONSIDERATION OF ENVIRONMENTAL CLEARANCE S.No Proposal Environmental Clearance for proposed river bed Sand mining having area 3.20 Ha of Garanda sand ghat on Pench River. S. State District Tehsil Village (1) No. (1.) Maharashtra Nagpur Parseoni Garanda [SIA/MH/MIN/160896/2020 , SIA/MH/MIN/160896/2020 ] Environmental Clearance for proposed river bed Sand mining having area 3.00 Ha of Ghatrohna sand ghat on Pench River. S. State District Tehsil Village (2) No. (1.) Maharashtra Nagpur Parseoni Ghatrohna [SIA/MH/MIN/161028/2020 , SIA/MH/MIN/161028/2020 ] Environmental Clearance for proposed river bed Sand mining having area 2.00 Ha of Palora sand ghat on Pench River. S. State District Tehsil Village (3) No. (1.) Maharashtra Nagpur Parseoni Palora [SIA/MH/MIN/161155/2020 , SIA/MH/MIN/161155/2020 ] Environmental Clearance for proposed river bed Sand mining having area 1.93 Ha of Pipla sand ghat on Pench River. S. State District Tehsil Village (4) No. (1.) Maharashtra Nagpur Parseoni Pipla [SIA/MH/MIN/161233/2020 , SIA/MH/MIN/161233/2020 ] Environmental Clearance for proposed river bed Sand mining having area 4.50 Ha of Sihora sand ghat on Kanhan River. (5) S. State District Tehsil Village No. (1.) Maharashtra Nagpur Parseoni Sihora [SIA/MH/MIN/161345/2020 , SIA/MH/MIN/161345/2020 ] Environmental Clearance for proposed river bed Sand mining having area 4.40 Ha of Singardip sand ghat on Kanhan River S. -

List of Dams in India: State Wise
ambitiousbaba.com Online Test Series List of Dams in India: State Wise State DAM and Location Rajasthan • RanapratapSagar Dam(Chambal River), at Rawatbhata • Mahi Bajaj Sagar Dam (Mahi River) at Banswara district • Bisalpur Dam (Banas River), At Tonk district • Srisailam Dam(Krishna River), at Kurnool Andhra Pradesh district • Somasila Dam (Penna River), at Nellore district • Prakasam Barrage (Krishna River), at Krishna and Guntur • Tatipudi Reservoir(River Gosthani ), at Tatipudi, Vizianagaram • Gandipalem Reservoir (River Penner) • Ramagundam dam (Godavari), in Karimnagar • Dummaguden Dam (river Godavari) Telangana • Nagarjuna Sagar Dam (Krishna river), at Nagarjuna Sagar Nalgonda • Sri Ram Sagar (River Godavari) • Nizam Sagar Dam (Manjira River) • Dindi Reservoir (River Krishna), at Dindi, Mahabubnagar town • Lower Manair Dam (Manair River) • Singur Dam (river Manjira) Bihar • Kohira Dam (Kohira River), at Kaimur district • Nagi Dam (Nagi River), in Jamui District Chhattisgarh • HasdeoBango Dam (Hasdeo River), at Korba district Gujarat • SardarSarovar Dam(Narmada river), at Navagam • Ukai Dam(Tapti River), at Ukai in Tapi district IBPS | SBI | RBI | SEBI | SIDBI | NABARD | SSC CGL | SSC CHSL | AND OTHER GOVERNMENT EXAMS 1 ambitiousbaba.com Online Test Series • Kadana Dam( Mahi River), at Panchmahal district • Karjan Reservoir (Karjan river), at Jitgadh village of Nanded Taluka, Dist. Narmada Himachal Pradesh • Bhakra Dam (Sutlej River) in Bilaspur • The Pong Dam (Beas River ) • The Chamera Dam (River Ravi) at Chamba district J & K -

GRMB Annual Report 2016-17
Government of India Ministry of Water Resources, River Development & Ganga Rejuvenation Godavari River Management Board, Hyderabad ANNUAL REPORT 2016-17 ANNUAL REPORT 2016-17 GODAVARI RIVER MANAGEMENT BOARD th 5 Floor, Jalasoudha, ErrumManzil, Hyderabad- 500082 PREFACE It is our pleasure to bring out the first Annual Report of the Godavari River Management Board (GRMB) for the year 2016-17. The events during the past two years 2014-15 and 2015-16 after constitution of GRMB are briefed at a glance. The Report gives an insight into the functions and activities of GRMB and Organisation Structure. In pursuance of the A.P. Reorganization Act, 2014, Central Government constituted GRMB on 28th May, 2014 with autonomous status under the administrative control of Central Government. GRMB consists of Chairperson, Member Secretary and Member (Power) appointed by the Central Government and one Technical Member and one Administrative Member nominated by each of the Successor State. The headquarters of GRMB is at Hyderabad. GRMB shall ordinarily exercise jurisdiction on Godavari river in the States of Telangana and Andhra Pradesh in regard to any of the projects over head works (barrages, dams, reservoirs, regulating structures), part of canal network and transmission lines necessary to deliver water or power to the States concerned, as may be notified by the Central Government, having regard to the awards, if any, made by the Tribunals constituted under the Inter-State River Water Disputes Act, 1956. During the year 2016-17, GRMB was headed by Shri Ram Saran, as the Chairperson till 31st December, 2016, succeeded by Shri S. K. Haldar, Chief Engineer, NBO, CWC, Bhopal as in-charge Chairperson from 4th January, 2017. -
![Foreword Ea=H] Hkkjh M](https://docslib.b-cdn.net/cover/0205/foreword-ea-h-hkkjh-m-2310205.webp)
Foreword Ea=H] Hkkjh M
ea=h] Hkkjh m|ksx ,oa yksd m|e Hkkjr ljdkj] ubZ fnYyh & 110011 MINISTER OF HEAVY INDUSTRIES & PUBLIC ENTERPRISES GOVERNMENT OF INDIA, UDYOG BHAWAN, NEW DELHI - 110011 Foreword The Public Enterprises Survey (2012-13) is the 53rd Survey in the series being laid in the Paliament. It presents an overview of the performance of Central Public Sector Enterprises (CPSEs) as on 31.3.2013. There were as many as 277 CPSEs out of which 229 were operating CPSEs as on 31st March, 2013. The CPSEs, as a group, continued to perform well during 2012-13. 2. The Gross Turnover of operating CPSEs has increased from `18,22,049 crore in 2011-12 to `19,45,777 crore in 2012-13 with a growth rate of 6.79 per cent over the previous year. The Agriculture sector recorded the highest growth in turnover of 23.26 percent during 2012-13 over the previous year, followed by ‘manufacturing’ with 10.15 percent growth and the ‘electricity’ sector with a growth of 6.18 percent. The ‘services’ sector showed a decline in revenue of 3.16 percent from operations during 2012-13, whereas it had recorded a significant growth (13.03 percent) in 2011-12. 3. The net profit of profit making CPSEs went up from `1,25,929 crore in 2011-12 to ` 1,43,559 crore in 2012-13 registering a growth of 14.00 percent. The loss of loss making CPSEs also increased marginally from R27,683 crore to ` 28,260 crore. The rate of growth in loss at 2.08 percent has been considerably less this year as compared to the last year’s growth rate of 26.89 percent. -
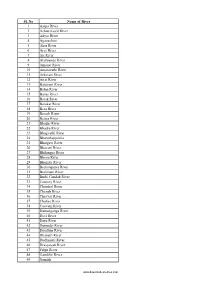
List of Rivers in India
Sl. No Name of River 1 Aarpa River 2 Achan Kovil River 3 Adyar River 4 Aganashini 5 Ahar River 6 Ajay River 7 Aji River 8 Alaknanda River 9 Amanat River 10 Amaravathi River 11 Arkavati River 12 Atrai River 13 Baitarani River 14 Balan River 15 Banas River 16 Barak River 17 Barakar River 18 Beas River 19 Berach River 20 Betwa River 21 Bhadar River 22 Bhadra River 23 Bhagirathi River 24 Bharathappuzha 25 Bhargavi River 26 Bhavani River 27 Bhilangna River 28 Bhima River 29 Bhugdoi River 30 Brahmaputra River 31 Brahmani River 32 Burhi Gandak River 33 Cauvery River 34 Chambal River 35 Chenab River 36 Cheyyar River 37 Chaliya River 38 Coovum River 39 Damanganga River 40 Devi River 41 Daya River 42 Damodar River 43 Doodhna River 44 Dhansiri River 45 Dudhimati River 46 Dravyavati River 47 Falgu River 48 Gambhir River 49 Gandak www.downloadexcelfiles.com 50 Ganges River 51 Ganges River 52 Gayathripuzha 53 Ghaggar River 54 Ghaghara River 55 Ghataprabha 56 Girija River 57 Girna River 58 Godavari River 59 Gomti River 60 Gunjavni River 61 Halali River 62 Hoogli River 63 Hindon River 64 gursuti river 65 IB River 66 Indus River 67 Indravati River 68 Indrayani River 69 Jaldhaka 70 Jhelum River 71 Jayamangali River 72 Jambhira River 73 Kabini River 74 Kadalundi River 75 Kaagini River 76 Kali River- Gujarat 77 Kali River- Karnataka 78 Kali River- Uttarakhand 79 Kali River- Uttar Pradesh 80 Kali Sindh River 81 Kaliasote River 82 Karmanasha 83 Karban River 84 Kallada River 85 Kallayi River 86 Kalpathipuzha 87 Kameng River 88 Kanhan River 89 Kamla River 90 -

A Regional Assessment of the Potential for Co2 Storage in the Indian Subcontinent
A REGIONAL ASSESSMENT OF THE POTENTIAL FOR CO2 STORAGE IN THE INDIAN SUBCONTINENT Technical Study Report No. 2008/2 May 2008 This document has been prepared for the Executive Committee of the IEA GHG Programme. It is not a publication of the Operating Agent, International Energy Agency or its Secretariat. INTERNATIONAL ENERGY AGENCY The International Energy Agency (IEA) was established in 1974 within the framework of the Organisation for Economic Co-operation and Development (OECD) to implement an international energy programme. The IEA fosters co-operation amongst its 26 member countries and the European Commission, and with the other countries, in order to increase energy security by improved efficiency of energy use, development of alternative energy sources and research, development and demonstration on matters of energy supply and use. This is achieved through a series of collaborative activities, organised under more than 40 Implementing Agreements. These agreements cover more than 200 individual items of research, development and demonstration. The IEA Greenhouse Gas R&D Programme is one of these Implementing Agreements. ACKNOWLEDGEMENTS AND CITATIONS This report was prepared as an account of the work sponsored by the IEA Greenhouse Gas R&D Programme. The views and opinions of the authors expressed herein do not necessarily reflect those of the IEA Greenhouse Gas R&D Programme, its members, the International Energy Agency, the organisations listed below, nor any employee or persons acting on behalf of any of them. In addition, none of these make any warranty, express or implied, assumes any liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product of process disclosed or represents that its use would not infringe privately owned rights, including any parties intellectual property rights. -

2020031344.Pdf
DISTRICT SURVEY REPORT (For Sand Mining) (As per Ministry of Environment, Forest and Climate Change, G.O.I, New Delhi; Notification No. S. O. 3611 (E), Dated - 25th July, 2018.) 2020 CHAPTER 1 INTRODUCTION Nagpur is the winter capital of the state of Maharashtra, a fast growing metropolis and third largest city in Maharashtra after Mumbai and Pune. With a population of 2,405,421 (2011) Nagpur Metropolitan Area is the 13th largest urban conglomeration in India. It has also recently been ranked as the cleanest city and the second greenest city of India. In addition to being the seat of annual winter session of Maharashtra state assembly “Vidhan Sabha”, Nagpur is also a major commercial and political center of the Vidharbha region of Maharashtra, and is also famous throughout the country as “Orange City” for being a major trade center of oranges that are cultivated in the region. In addition, the city also derives political importance from being the headquarters for the RSS and an important location for the Buddhistmovement. The city was founded by the Gonds but later became part of the Maratha Empire under the Bhonsles. The British East India Company took over Nagpur in the 19th century and made it the capital of the Central Provinces and Berar. After the first reorganization of states, the city lost its capital status but according to the “Nagpur Pact” between political leaders it was made the second capital of Maharashtra. Pic 1: Central Provinces and Berar, 1903. Nagpur is also called, “Tiger Capital of India” as it connects many Tiger Reserves in India to the world. -

Map-1: Forest Cover in Maharashtra
Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized ENVIRONMENT A D• SOCIAL NAGE ENT ~w.~. GRID CORPORATION 0 INDIA LTD. (A GOV.RN".NT 0' INDIA .NT•• ".' •• ) ESMD/FEARIWRSS-//(A)/01 Nov'09 ~EST AVAll -:SlE COpy CONTENTS Page No. SECTION I: PROJECT DESCRIPTION 1-3 - BACKGROUND 1 - BENEFITS OF THE PROJECT 1 - SCOPE OF WORK 3 SECTION II: BASELINE DATA 4-8 - MAHARASHTRA 4 - - MADHYA PRADESH 5 - - CHHATTISGARH 7 .. SECTION III: POLICY, LEGAL & REGULATORY FRAMEWORK 9-14 - - ENVIRONMENTAL 9 - - SOCIAL 12 - SECTION IV: MAJOR FEATURES OF FINAL ROUTE & ENV. IMPACT 15-24 - - ROUTE SELECTION 15 - 765 KV SIC SEONI-WARDHA LINE 17 - ENVIRONMENTAL IMPACT MATRIX 19 - - 400 KV DIC RAIPUR-WARDHA LINE 19 • - ENVIRONMENTAL IMPACT MATRIX 20 - 400 KV DIC BHADRAVATI-PARLI LINE 21 • - ENVIRONMENTAL IMPACT MATRIX 22 • - 400 KV DIC WARDHA-PARLI LINE 23 - ENVIRONMENTAL IMPACT MATRIX 24 • - 400 KV DIC PARLI-PARLI LINE 24 , . SECTION V: POTENTIAL ENV. IMPACT EVALUATION & ITS MANAGEMENT 25-35 • .. - IMPACT DUE TO PROJECT LOCATION 25 - ENVIRONMENTAL PROBLEM DUE TO DESIGN 27 - ENVIRONMENTAL PROBLEMS DURING CONSTRUCTION 29 - ENVIRONMENTAL PROBLEMS RESULTING FROM OPERATION 30 #I - CRITICAL ENVIRONMENTAL REVIEW CRITERIA 32 • - PUBLIC CONSULTATION 32 • - CONCLUSIONS 34 " SECTION VI: MONITORING & ORGANISATIONAL SUPPORT STRUCTURE 36-37 • - ENVIRONMENTAL MONITORING IN POWERGRID 36 • - ENVIRONMENT REVIEW 37 ENCLOSURES: - ANNEXURES 1 to 10 II • " "'ESTl~I~N R.EGION TR. S)'STEl\l (by 2011 - 12) EXHIBITw1 "S" CkRDA (KA~SAAI) TO SINGRAULI NAGDA RANCHORPURA (VADAVID , INDoRE \, , A 1:~~r~Q.r· o t ,/' a 0 LIMO! (CHORNA) 0 .'~' \ r .."eJ-. ,# DIU Proposed Project r~·· ..,; LEGEND , PARLI (MSEBY ..