Analytical Caustic Surfaces
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On Caustics by Reflexion
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Topology. Vol. 21. No. 2. pp. 179-199, 1982 W&9383/82/020179-21$03.00/O Printed in Great Britain. Pergamon Press Ltd. ON CAUSTICS BY REFLEXION J. W. BRUCE,t P. J. GIBLIN and C. G. GIBSON (Received 21 May 1980) ONE OF THE fundamental contributions of singularity theory to the physical sciences is the result of Looijenga, discussed in the opening section of this paper, that a generic wavefront gives rise to a caustic whose local structure can be described by a finite number of archetypes. However, when caustics arise in explicit physical situations, there is no reason a priori to suppose that a generic state of the system will necessarily give rise to a generic caustic. In this paper we make a detailed study of the system comprising a mirror M (a smooth hypersurface in R”+‘) and a point source of light L (a point in R”+‘): light rays emanating from L are reflected at M and give rise to a caustic by reflexion, the envelope of the family of reflected rays. And the problem to which we address ourselves is whether a generic state of our system does give rise to a generic caustic. Note that we consider only first reflexions of light from M. Perhaps the most natural question to look at here is that of mirror genericity, i.e. for a fixed position of the source L will a generic mirror M give rise to a generic caustic? We give an affirmative answer to this question, using a classical geometric construction, under the hypotheses that the mirror M is compact and has everywhere positive Gaussian curvature, and the source L lies inside M. -

Steiner's Hat: a Constant-Area Deltoid Associated with the Ellipse
STEINER’S HAT: A CONSTANT-AREA DELTOID ASSOCIATED WITH THE ELLIPSE RONALDO GARCIA, DAN REZNIK, HELLMUTH STACHEL, AND MARK HELMAN Abstract. The Negative Pedal Curve (NPC) of the Ellipse with respect to a boundary point M is a 3-cusp closed-curve which is the affine image of the Steiner Deltoid. Over all M the family has invariant area and displays an array of interesting properties. Keywords curve, envelope, ellipse, pedal, evolute, deltoid, Poncelet, osculat- ing, orthologic. MSC 51M04 and 51N20 and 65D18 1. Introduction Given an ellipse with non-zero semi-axes a,b centered at O, let M be a point in the plane. The NegativeE Pedal Curve (NPC) of with respect to M is the envelope of lines passing through points P (t) on the boundaryE of and perpendicular to [P (t) M] [4, pp. 349]. Well-studied cases [7, 14] includeE placing M on (i) the major− axis: the NPC is a two-cusp “fish curve” (or an asymmetric ovoid for low eccentricity of ); (ii) at O: this yielding a four-cusp NPC known as Talbot’s Curve (or a squashedE ellipse for low eccentricity), Figure 1. arXiv:2006.13166v5 [math.DS] 5 Oct 2020 Figure 1. The Negative Pedal Curve (NPC) of an ellipse with respect to a point M on the plane is the envelope of lines passing through P (t) on the boundary,E and perpendicular to P (t) M. Left: When M lies on the major axis of , the NPC is a two-cusp “fish” curve. Right: When− M is at the center of , the NPC is 4-cuspE curve with 2-self intersections known as Talbot’s Curve [12]. -

Analytical Caustic Surfaces
NASA Technical Memorandum 87805 Analytical Caustic Surfaces R. F. Schmidt APRIL 1987 NASA CONTENTS ABSTRACT ..................................................... v NOTATION ..................................................... vii INTRODUCTION .................................................. 1 CENTER SURFACES ............................................... 7 CAUSTICS FROM DISTORTED WAVEFRONTS ................................ 11 CAUSTICS FROM FLUX DENSITY SINGULARITIES ............................. 14 CAUSTICS FROM A TENSOR ALGORITHM .................................. 24 CONCLUSION .................................................... 27 ACKNOWLEDGMENTS ............................................... 28 REFERENCES .................................................... 29 APPENDIX A - Gauss/Seidel Aberrations (Parallel Distortion of Gaussian Wavefront) ............ 31 APPENDIX B - Gauss/Seidel Aberrations (Normal Distortion of Gaussian Wavefront) ............ 33 APPENDIX C - The Caustic Surfaces of a Paraboloid and Inclined Plane Wave ............... 39 PRECEDING PAGE BLM NOT FKMED iii NOTATION EV Evolute INV Involute A Wavefront c2 Caustic surface of two branches (wl, wl) si,- s, Incident and reflected rays N Normal to a surface LC,, LCZ Lines of curvature E,, E2 Characteristic directions (eigenvectors on a wavefront) ki, kZ Characteristic values (eigenvalues), principal normal curvatures KN.KG. KM Normal, Gaussian, and mean curvatures --x = (x, Y, z) Generic parametric surface coordinates ---x., X" Tangents to a surface XUU, X"", X"" Tangent -

Collected Atos
Mathematical Documentation of the objects realized in the visualization program 3D-XplorMath Select the Table Of Contents (TOC) of the desired kind of objects: Table Of Contents of Planar Curves Table Of Contents of Space Curves Surface Organisation Go To Platonics Table of Contents of Conformal Maps Table Of Contents of Fractals ODEs Table Of Contents of Lattice Models Table Of Contents of Soliton Traveling Waves Shepard Tones Homepage of 3D-XPlorMath (3DXM): http://3d-xplormath.org/ Tutorial movies for using 3DXM: http://3d-xplormath.org/Movies/index.html Version November 29, 2020 The Surfaces Are Organized According To their Construction Surfaces may appear under several headings: The Catenoid is an explicitly parametrized, minimal sur- face of revolution. Go To Page 1 Curvature Properties of Surfaces Surfaces of Revolution The Unduloid, a Surface of Constant Mean Curvature Sphere, with Stereographic and Archimedes' Projections TOC of Explicitly Parametrized and Implicit Surfaces Menu of Nonorientable Surfaces in previous collection Menu of Implicit Surfaces in previous collection TOC of Spherical Surfaces (K = 1) TOC of Pseudospherical Surfaces (K = −1) TOC of Minimal Surfaces (H = 0) Ward Solitons Anand-Ward Solitons Voxel Clouds of Electron Densities of Hydrogen Go To Page 1 Planar Curves Go To Page 1 (Click the Names) Circle Ellipse Parabola Hyperbola Conic Sections Kepler Orbits, explaining 1=r-Potential Nephroid of Freeth Sine Curve Pendulum ODE Function Lissajous Plane Curve Catenary Convex Curves from Support Function Tractrix -

A Handbook on Curves and Their Properties
SEELEY G. 1 1UDD LIBRARY LAWRENCE UNIVERSITY Appleton, Wisconsin «__ CURVES AND THEIR PROPERTIES A HANDBOOK ON CURVES AND THEIR PROPERTIES ROBERT C. YATES United States Military Academy J. W. EDWARDS — ANN ARBOR — 1947 97226 NOTATION octangular C olar Coordin =r.t^r ini Tangent and the Rad ,- ^lem a Copyright 1947 by R m Origin to Tangent. i i = /I. f(s ) = C well Intrinsic Egua 9 ;(f «r,p) = C 1- Lithoprinted by E rlll CONTENTS PREFACE nephroid and teacher lume proposes to supply to student curves. Rather ,n properties of plane Pedal Curves e Pedal Equations U vhi C h might be found ^ Yc 31 r , 'f Lr!-ormation and in engine useful in the classroom 3 aid in the s Radial Curves alphabetical arrangement is Roulettes Semi-Cubic Parabola Sketching Evolutes, Curve Sketching, and Spirals Strophoid If 1 :s readily understandable. Trigonometric Functions .... Trochoids Witch of Agnesi bfi Stropho: i including the Astroid, HISTORY: The Cycloidal curves, discovered by Roemer (1674) In his search for the Space Is provided occasionally for the reader to ir ;,„ r e for gear teeth. Double generation was first sert notes, proofs, and references of his own and thus be st form noticed by Daniel Bernoulli in 1725- It is with pleasure that the author acknowledges a hypo loid o f f ur valuable assistance in the composition of this work. 1. DESCRIPTION: The d is y Mr. H. T. Guard criticized the manuscript and offered Le roll helpful suggestions; Mr. Charles Roth and Mr. William radius four Lmes as la ge- -oiling upon the ins fixed circle (See Epicycloids) ASTROID EQUATIONS: = cos 1 1 1 (f)(3 x + - a y sin [::::::: = (f)(3 :ion: (Fig. -

The Cissoid of Diocles
Playing With Dynamic Geometry by Donald A. Cole Copyright © 2010 by Donald A. Cole All rights reserved. Cover Design: A three-dimensional image of the curve known as the Lemniscate of Bernoulli and its graph (see Chapter 15). TABLE OF CONTENTS Preface.................................................................................................................. xix Chapter 1 – Background ............................................................ 1-1 1.1 Introduction ............................................................................................................ 1-1 1.2 Equations and Graph .............................................................................................. 1-1 1.3 Analytical and Physical Properties ........................................................................ 1-4 1.3.1 Derivatives of the Curve ................................................................................. 1-4 1.3.2 Metric Properties of the Curve ........................................................................ 1-4 1.3.3 Curvature......................................................................................................... 1-6 1.3.4 Angles ............................................................................................................. 1-6 1.4 Geometric Properties ............................................................................................. 1-7 1.5 Types of Derived Curves ....................................................................................... 1-7 1.5.1 Evolute -

MF-$0.75 HC Not Available from EDRS. PLUS POSTAGE Geometry
DOCUMENT RESUME ED 100 648 SE 018 119 AUTHOR Yates, Robert C. TITLE Curves and Their Properties. INSTITUTION National Council of Teachers of Mathematics, Inc., Washington, D.C. PUB DATE 74 NOTE 259p.; Classics in Mathematics Education, Volume 4 AVAILABLE FROM National Council of Teachers of Mathematics, Inc., 1906 Association Drive, Reston, Virginia 22091 ($6.40) EDRS PRICE MF-$0.75 HC Not Available from EDRS. PLUS POSTAGE DESCRIPTORS Analytic Geometry; *College Mathematics; Geometric Concepts; *Geometry; *Graphs; Instruction; Mathematical Enrichment; Mathematics Education;Plane Geometry; *Secondary School Mathematics IDENTIFIERS *Curves ABSTRACT This volume, a reprinting of a classic first published in 1952, presents detailed discussions of 26 curves or families of curves, and 17 analytic systems of curves. For each curve the author provides a historical note, a sketch orsketches, a description of the curve, a a icussion of pertinent facts,and a bibliography. Depending upon the curve, the discussion may cover defining equations, relationships with other curves(identities, derivatives, integrals), series representations, metricalproperties, properties of tangents and normals, applicationsof the curve in physical or statistical sciences, and other relevantinformation. The curves described range from thefamiliar conic sections and trigonometric functions through tit's less well knownDeltoid, Kieroid and Witch of Agnesi. Curve related - systemsdescribed include envelopes, evolutes and pedal curves. A section on curvesketching in the coordinate plane is included. (SD) U S DEPARTMENT OFHEALTH. EDUCATION II WELFARE NATIONAL INSTITUTE OF EDUCATION THIS DOCuME N1 ITASOLE.* REPRO MAE° EXACTLY ASRECEIVED F ROM THE PERSON ORORGANI/AlICIN ORIGIN ATING 11 POINTS OF VIEWOH OPINIONS STATED DO NOT NECESSARILYREPRE INSTITUTE OF SENT OFFICIAL NATIONAL EDUCATION POSITION ORPOLICY $1 loor oiltyi.4410,0 kom niAttintitd.: t .111/11.061 . -

2Dcurves in .Pdf Format (1882 Kb) Curve Literature Last Update: 2003−06−14 Higher Last Updated: Lennard−Jones 2002−03−25 Potential
2d curves A collection of 631 named two−dimensional curves algebraic curves are a polynomial in x other curves and y kid curve line (1st degree) 3d curve conic (2nd) cubic (3rd) derived curves quartic (4th) sextic (6th) barycentric octic (8th) caustic other (otherth) cissoid conchoid transcendental curves curvature discrete cyclic exponential derivative fractal envelope gamma & related hyperbolism isochronous inverse power isoptic power exponential parallel spiral pedal trigonometric pursuit reflecting wall roulette strophoid tractrix Some programs to draw your own For isoptic cubics: curves: • Isoptikon (866 kB) from the • GraphEq (2.2 MB) from University of Crete Pedagoguery Software • GraphSight (696 kB) from Cradlefields ($19 to register) 2dcurves in .pdf format (1882 kB) curve literature last update: 2003−06−14 higher last updated: Lennard−Jones 2002−03−25 potential Atoms of an inert gas are in equilibrium with each other by means of an attracting van der Waals force and a repelling forces as result of overlapping electron orbits. These two forces together give the so−called Lennard−Jones potential, which is in fact a curve of thirteenth degree. backgrounds main last updated: 2002−11−16 history I collected curves when I was a young boy. Then, the papers rested in a box for decades. But when I found them, I picked the collection up again, some years spending much work on it, some years less. questions I have been thinking a long time about two questions: 1. what is the unity of curve? Stated differently as: when is a curve different from another one? 2. which equation belongs to a curve? 1. -
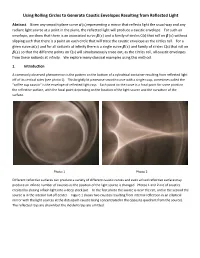
Using Rolling Circles to Generate Caustic Envelopes Resulting from Reflected Light
Using Rolling Circles to Generate Caustic Envelopes Resulting from Reflected Light Abstract. Given any smooth plane curve ( )representing a mirror that reflects light the usual way and any radiant light source at a point in the plane, the reflected light will produce a caustic envelope. For such an 휶 푠 envelope, we show that there is an associated curve ( ) and a family of circles C(s) that roll on ( ) without slipping such that there is a point on each circle that will trace the caustic envelope as the circles roll. For a 휷 푠 휷 푠 given curve ( ) and for all radiants at infinity there is a single curve ( ) and family of circles C(s) that roll on ( ) so that the different points on C(s) will simultaneously trace out, as the circles roll, all caustic envelopes 휶 푠 휷 푠 from these radiants at infinity. We explore many classical examples using this method. 휷 푠 1. Introduction A commonly observed phenomenon is the pattern on the bottom of a cylindrical container resulting from reflected light off of its vertical sides (see photo 1). This brightly lit piecewise smooth curve with a single cusp, sometimes called the “coffee cup caustic” is the envelope of reflected light rays. Each point on the curve is a focal point for some point on the reflective surface, with the focal point depending on the location of the light source and the curvature of the surface. Photo 1 Photo 2 Different reflective surfaces can produce a variety of different caustic curves and even a fixed reflective surface may produce an infinite number of caustics as the position of the light source is changed. -

Caustics of Light Rays and Euler's Angle of Inclination
Caustics of Light Rays and Euler's Angle of Inclination S. Koshkin and I. Rocha Abstract - Euler used intrinsic equations expressing the radius of curvature as a function of the angle of inclination to find curves similar to their evolutes. We interpret the evolute of a plane curve optically, as the caustic (envelope) of light rays normal to it, and study the Euler's problem for general caustics. The resulting curves are characterized when the rays are at a constant angle to the curve, generalizing the case of evolutes. Aside from analogs of classical solutions we encounter some new types of curves. We also consider caustics of parallel rays reflected by a curved mirror, where Euler's problem leads to a novel pantograph equation, and describe its analytic solutions. Keywords : plane curve; evolute; intrinsic equations; angle of inclination; caustic; delay differential equation; pantograph equation Mathematics Subject Classification (2020) : 53A04; 78A05; 34K06; Introduction Caustic, from Latin \burn", is a curve or surface that is particularly brightly lit. In geometric optics this happens because all light rays are tangent to it, and hence the light concentrates near it. A special class of caustics, caustics by reflection or catacaustics (from Greek catoptron, mirror), were introduced by Tschirnhaus in 1682 [14, 21]. For them the rays come from a point source reflected in a curved mirror. Determining catacaustics was an important test case for the early calculus methods. Jacob Bernoulli studied them around 1692, and L'Hopital's calculus textbook (1696) included two chapters on them [2]. As Bernoulli and l'Hopital already realized, evolutes of plane curves, the sets of their centers of curvature, can be interpreted as a special case of caustics, when the light rays are normal to the curve. -
101 Symbolic Geometry Examples
101 Symbolic Geometry Examples INTRODUCTION ................................................................................................................................................................... 1 Example 1: Median & Angle Bisector of a Right Triangle ................................................................................................................. 2 Example 2: Angles and Circles .......................................................................................................................................................... 3 Example 3: Rectangle Circumscribing an Equilateral Triangle .......................................................................................................... 5 Example 4: Area of a Hexagon bounded by Triangle side trisectors .................................................................................................. 6 Incircles / circumcircles / excircles / areas .................................................................................................................................................. 9 Example 5: Circumcircle Radius ........................................................................................................................................................ 9 Example 6: Incircle Radius .............................................................................................................................................................. 15 Example 7: Incircle Center in Barycentric Coordinates .................................................................................................................. -

Caustics by Reflection Curves of Direction Rational Arc Length Part
Caustics by reflection Curves of direction Rational arc length Part - XII C. Masurel 09/05/2015 (Draft : V2) Abstract Caustics by reflection and curves of direction have, when algebraic as shown by Laguerre and Humbert, a rational arc length. Examples of low order caustics are drawn with help of geometric definition of catacaustics. For conics the caustic is in general of order 6. We present links with classes of curves of direction studied by Cesaro, Balitrand and Goormaghtigh in NAM between 1885 and 1920. 1 Plane caustics by reflection. Caustics of plane curves are defined as the envelope of the light rays coming from a ponctual source and reflected or refracted in a given curve. We only study in this paper the first type of caustics (reflection) and never caustics by refraction so we drop the precision and call them caustics. Caustics by reflection (sometimes called catacaustics) seem to go back to Tschirn- hausen and his paper of 1682 but Apollonius knew some properties of foci of conics (the light rays from a focus converge in the other focus). For the parbola : parallele rays to the axis of symetry from infinity converge at the only focus, which is a caustic. Two cases of caustics can be distinguished : - Light rays coming from a ponctual source of light at finite distance, - Light rays coming from a point at infinity, In the first case light rays diverge from a point and in the second light rays are parallele. The transformation of the initial curve is a tangential transformation that maps tangents of the first curve to tangents of the caustic.