Mapping Farmland Wader Distributions and Population Change to Identify Wader Priority Areas for Conservation and Management Action
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Introduction the Place-Names in This Book Were Collected As Part of The
Introduction The place-names in this book were collected as part of the Arts and Humanities Research Board-funded (AHRB) ‘Norse-Gaelic Frontier Project, which ran from autumn 2000 to summer 2001, the full details of which will be published as Crawford and Taylor (forthcoming). Its main aim was to explore the toponymy of the drainage basin of the River Beauly, especially Strathglass,1 with a view to establishing the nature and extent of Norse place-name survival along what had been a Norse-Gaelic frontier in the 11th century. While names of Norse origin formed the ultimate focus of the Project, much wider place-name collection and analysis had to be undertaken, since it is impossible to study one stratum of the toponymy of an area without studying the totality. The following list of approximately 500 names, mostly with full analysis and early forms, many of which were collected from unpublished documents, has been printed out from the Scottish Place-Name Database, for more details of which see Appendix below. It makes no claims to being comprehensive, but it is hoped that it will serve as the basis for a more complete place-name survey of an area which has hitherto received little serious attention from place-name scholars. Parishes The parishes covered are those of Kilmorack KLO, Kiltarlity & Convinth KCV, and Kirkhill KIH (approximately 240, 185 and 80 names respectively), all in the pre-1975 county of Inverness-shire. The boundaries of Kilmorack parish, in the medieval diocese of Ross, first referred to in the medieval record as Altyre, have changed relatively little over the centuries. -

The Hillforts of Strathdon: 2004-2010
The Hillforts of Strathdon: 2004-2010 Murray Cook Having worked across Scotland and Northern England for the last 15 years I can say without hesitation that projects with Ian in Aberdeenshire always filled me with joy and renewed passion and enthusiasm for archaeology: without him this project would not have taken place. Introduction In ‘ In the Shadow of Bennachie’ the RCAHMS survey of the Strathdon area, the hillforts (throughout the paper ‘hillfort’ is used as shorthand to describe an enclosure whether on a hill or not) of the area were classified into a six-fold scheme, according to size and defensive system recorded (RCAHMS 2007, 100-1). Of course, the information was gathered through non-invasive survey, and it is unclear how these classes related to each other, as their dates were unknown. Using the same criteria of size and defensive system, albeit with a larger data set Ralston ( et al 1983) proposed a different classification as did Feachem a generation earlier (1966). These conflicting classifications illustrate the essentially limited value of such attempts: without hard data they remain talking points to be reinterpreted once a generation. In order to further the debate - hard dating evidence from physical excavation is needed. In what some have described as naïve, The Hillforts of Strathdon Project was set up in an attempt to characterise and date the type-sites of the area, through a programme of key- hole excavation on the variety of enclosures in the area. After six seasons of excavations on nine enclosures with local volunteers and students, this paper briefly summarises the key results in chronological order and the general conclusions. -
Studies of the Foods and Feeding Ecology of Wading Birds
STUDIES OF THE FOODS AND FEEDING ECOLOGY OF WADING BIRDS Thesis submitted in part fulfilment of the requirements for the degree of Doctor of Philosophy of the Council for National Academic Awards .. by Malcolm E. Greenhalgh, B. A. Department of Biology Liverpool Polytechnic October 1975 s ABSTRACT In this thesis are described the populations of waders (Aves: Charadrii) occurring on the Ribble Estuary, Lancashire, special reference being made to the eleven species comprising the bulk of the shore wader population. The daily routine of these birds is described including the time spent in feeding. The feeding areas are described together with the foods taken from gut and pellet analysis and direct observation. The distributions of invertebrates, and especially those of major importance as wader food, are described as well as the factors affecting these distributions. Variations in density of prey in relation to O. D., general geography of the estuary, and time of year are included. Depth distribution and variations in prey size are outlined for the main species. Food intake was studied in the eight main waders. Daily intake through the year is described. in relation to energy requirements. Variations of feeding rates with several factors are included. All data are combined to enable calculation of the total biomasses of the main prey taken by waders in the course of a year. These are compared with total minimum annual production of the prey. Future work, including a computer study based on these and extra data, is outlined. Frontispiece a. The author counting a flock of 45,000 Knot 25 August, 1972 b. -

The Gunn Herald
THE GUNN HERALD THE INTERNATIONAL JOURNAL OF THE CLAN GUNN SOCIETY Published tri-annually in February, June and October Volume no. 91: October 2013 CONTENTS Office Bearers Inside front cover Contents Page 1 Editorial Page 2 President’s Message Page 3 The First Clan Gunn Magazine Page 4 Commemoration of the Kildonan Clearances Page 5 The Clan Gunn at Ashbourne Page 7 The Canadian Summer Festival Circuit Page 9 Walter Scott & Russia Page 11 What’s in a name? Page 13 Membership Report Page 15 1 EDITORIAL anything, lamented living so far from Afternoon all, London’s flagship Topshop. However, when I was 18 and moved down to Exeter to go to For those of you who don’t know already University I was part of only 7 people whom I will be attempting to fill some very big I ever met there who were Scottish. People boots left by Dave Taylor in the role of looked at me in amazement when I told them Editor of the Herald. For the more regular where I was from, incredulous that anyone attendees of clan events my face may be a would travel so far. Or indeed, disbelieving rather distant memory as it has been a few that anyone who was not a gravy-loving years since my last Clan Gunn Gathering. cretin could exist north of the border. I began Three years at University and a good few to be at first defensive of my heritage and summer jaunts to distant sunspots always then proud, I loved that I was part of such a seemed to coincide with festivities in the minority, that people asked me questions North and it is with regret that I must inform about life in Edinburgh as if I’d just stashed you I am no longer 4ft tall, wear t-shirts my loincloth and crawled out deepest, proclaiming my status as “big sister” and darkest Peru. -

Timetable from Monday 16Th August 2021
Timetable from Monday 16th August 2021 Days of Operation Monday to Friday Service Number 21 Service Description Dingwall - Cromarty Service No. 21 21 21 21B 21 21 21 21B 21 Sch MWF F MW F F NF Sch #Sch Sch Sch Dingwall Academy - - - Z1335 - - - Z1545 - Dingwall Tesco - 0845 1215 1337 1405 1435 1435 1547 1745 Dingwall Hill Street - 0850 1220 1339 1410 1440 1440 1549 1750 Maryburgh - - - 1342 - - - 1552 - Conon Bridge - - - 1345 - - - 1555 - Easter Kinkell - 0903 1233 1355 1423 1453 1453 1605 1803 Culbokie Shops - 0910 1240 1402 1430 1500 1500 1612 1810 Culbokie School Croft - 0913 1243 1405 1433 1503 1503 1615 1813 Resolis Primary School 0843 - 1250 - 1440 1510 1510 - - Balbalir Aird Place 0845 - 1252 - 1442 1512 - - - Newhall Ellenslea 0847 - 1254 - 1444 1514 - - - Jemimaville 0851 - 1258 - 1448 1518 - - - Cromarty 0859 - 1306 - 1456 1526 - - - Codes: MWF Mon Wed Fri only Sch Schooldays only F Fridays only #Sch School holidays only MW Monday & Wednesday Z1 Use Stance 2 at Dingwall Academy NF Not Fridays Days of Operation Monday to Friday Service Number 21 Service Description Dingwall - Cromarty Service No. 21B 21B 21 21 21 21B 21 21 21 21 Sch #Sch MWF MW F F Sch NF NF F #Sch Sch Sch Sch Sch Cromarty - - 0925 1310 1325 1325 1445 - 1456 - Jemimaville - - 0933 1318 1333 1333 1453 - 1504 1538 Newhall Ellenslea - - 0937 1322 C1337 1338 1456 - 1507 1541 Balblair Aird Place - - 0939 1324 1339 - 1459 - 1510 1543 Resolis Primary School - - 0941 1326 1341 - 1501 - 1512 1546 Springfield - - - - - 1348 - - - - Culbokie Easter Culbo Jct - - - - - -

United Kingdom Ordnance Survey Seventh Series
University of Waikato Library: Map Collection United Kingdom: Ordnance Survey Maps of England, Scotland and Wales. 1: 63,360 Seventh Series The Map Collection of the University of Waikato Library contains a comprehensive collection of maps from around the world with detailed coverage of New Zealand and the Pacific. These maps were issued in the 1950s and 1960s. The maps are held in Unit A Drawers 4 & 5. Please ask a librarian if you would like to use one. Key map on page 4 1 Shetland Islands (Yell and Unst) 29 Elgin 2 Shetland Islands (North Mainland) 30 Banff 3 Shetland Islands (Lerwick) 31 Peterhead 4 Shetland Islands (South Mainland) 32 Barra 5 Orkney Islands (North) 33 Rhum and part of Skye 6 Orkney Islands (Kirkwall) 34 South Skye and Arisaig 7 Pentland Firth 35 Loch Arkaig 8 Isle of Lewis 36 Fort Augustus 9 Cape Wrath 37 Kingussie 10 Tongue 38 Grantown & Cairngorm 11 Thurso 39 Strathdon 12 Island of Lewis and North Harris 40 Aberdeen 13 Loch Inver & Loch Assynt 41 Braemar 14 Lairg 42 Ballater 15 Helmsdale 43 Stonehaven 16 Wick 44 Coll & Tiree 17 North Uist 45 Sound of Mull 18 Harris 46 Loch Linnhe 19 Gairloch 47 Glen Coe 20 Ullapool 48 Loch Tay 21 Bonar-Bridge 49 Blairgowrie 22 Dornoch 50 Forfar 23 South Uist 51 Iona & Colonsay 24 North Skye 52 Loch Awe 25 Portree 53 Loch Lomond 26 Lochcarron 54 Stirling 27 Strathpeffer 55 Perth & Alloa 28 Inverness 56 St.Andrews & Kirkcaldy Page 1 of 4 Last updated May 2013 University of Waikato Library: Map Collection United Kingdom: Ordnance Survey Maps of England, Scotland and Wales. -

Falkirk Wheel, Scotland
Falkirk Wheel, Scotland Jing Meng Xi Jing Fang Natasha Soriano Kendra Hanagami Overview Magnitudes & Costs Project Use and Social and Economic Benefits Technical Issues and Innovations Social Problems and Policy Challenges Magnitudes Location: Central Scotland Purpose: To connecting the Forth and Clyde canal with the Union canal. To lift boats from a lower canal to an upper canal Magnitudes Construction Began: March 12, 1999 Officially at Blairdardie Road in Glasgow Construction Completed: May 24, 2002 Part of the Millennium Link Project undertaken by British Waterways in Scotland To link the West and East coasts of Scotland with fully navigable waterways for the first time in 35 years Magnitudes The world’s first and only rotating boat wheel Two sets of axe shaped arms Two diametrically opposed waterwater-- filled caissons Magnitudes Overall diameter is 35 meters Wheel can take 4 boats up and 4 boats down Can overcome the 24m vertical drop in 15 minute( 600 tones) To operate the wheel consumes just 1.5 kilowattkilowatt--hourshours in rotation Costs and Prices Total Cost of the Millennium Link Project: $123 M $46.4 M of fund came from Nation Lottery Falkirk Wheel Cost: $38.5 M Financing Project was funded by: British Waterways Millennium Commission Scottish Enterprise European Union Canalside local authorities Fares for Wheel The Falkirk Wheel Experience Tour: Adults $11.60 Children $6.20 Senior $9.75 Family $31.20 Social Benefits Proud Scots Queen of Scotland supported the Falkirk Wheel revived an important -

Rosehall Information
USEFUL TELEPHONE NUMBERS Rosehall Information POLICE Emergency = 999 Non-emergency NHS 24 = 111 No 21 January 2021 DOCTORS Dr Aline Marshall and Dr Scott Smith PLEASE BE AWARE THAT, DUE TO COVID-RELATED RESTRICTIONS Health Centre, Lairg: tel 01549 402 007 ALL TIMES LISTED SHOULD BE CHECKED Drs C & J Mair and Dr S Carbarns This Information Sheet is produced for the benefit of all residents of Creich Surgery, Bonar Bridge: tel 01863 766 379 Rosehall and to welcome newcomers into our community DENTISTS K Baxendale / Geddes: 01848 621613 / 633019 Kirsty Ramsey, Dornoch: 01862 810267; Dental Laboratory, Dornoch: 01862 810667 We have a Village email distribution so that everyone knows what is happening – Golspie Dental Practice: 01408 633 019; Sutherland Dental Service, Lairg: 402 543 if you would like to be included please email: Julie Stevens at [email protected] tel: 07927 670 773 or Main Street, Lairg: PHARMACIES 402 374 (freephone: 0500 970 132) Carol Gilmour at [email protected] tel: 01549 441 374 Dornoch Road, Bonar Bridge: 01863 760 011 Everything goes out under “blind” copy for privacy HOSPITALS / Raigmore, Inverness: 01463 704 000; visit 2.30-4.30; 6.30-8.30pm There is a local residents’ telephone directory which is available from NURSING HOMES Lawson Memorial, Golspie: 01408 633 157 & RESIDENTIAL Wick (Caithness General): 01955 605 050 the Bradbury Centre or the Post Office in Bonar Bridge. Cambusavie Wing, Golspie: 01408 633 182; Migdale, Bonar Bridge: 01863 766 211 All local events and information can be found in the -

Walks and Scrambles in the Highlands
Frontispiece} [Photo by Miss Omtes, SLIGACHAN BRIDGE, SGURR NAN GILLEAN AND THE BHASTEIR GROUP. WALKS AND SCRAMBLES IN THE HIGHLANDS. BY ARTHUR L. BAGLEY. WITH TWELVE ILLUSTRATIONS. Xon&on SKEFFINGTON & SON 34 SOUTHAMPTON STREET, STRAND, W.C. PUBLISHERS TO HIS MAJESTY THE KING I9H Richard Clav & Sons, Limiteu, brunswick street, stamford street s.e., and bungay, suffolk UNiVERi. CONTENTS BEN CRUACHAN ..... II CAIRNGORM AND BEN MUICH DHUI 9 III BRAERIACH AND CAIRN TOUL 18 IV THE LARIG GHRU 26 V A HIGHLAND SUNSET .... 33 VI SLIOCH 39 VII BEN EAY 47 VIII LIATHACH ; AN ABORTIVE ATTEMPT 56 IX GLEN TULACHA 64 X SGURR NAN GILLEAN, BY THE PINNACLES 7i XI BRUACH NA FRITHE .... 79 XII THROUGH GLEN AFFRIC 83 XIII FROM GLEN SHIEL TO BROADFORD, BY KYLE RHEA 92 XIV BEINN NA CAILLEACH . 99 XV FROM BROADFORD TO SOAY . 106 v vi CONTENTS CHAF. PACE XVI GARSBHEINN AND SGURR NAN EAG, FROM SOAY II4 XVII THE BHASTEIR . .122 XVIII CLACH GLAS AND BLAVEN . 1 29 XIX FROM ELGOL TO GLEN BRITTLE OVER THE DUBHS 138 XX SGURR SGUMA1N, SGURR ALASDAIR, SGURR TEARLACH AND SGURR MHIC CHOINNICH . I47 XXI FROM THURSO TO DURNESS . -153 XXII FROM DURNESS TO INCHNADAMPH . 1 66 XXIII BEN MORE OF ASSYNT 1 74 XXIV SUILVEN 180 XXV SGURR DEARG AND SGURR NA BANACHDICH . 1 88 XXVI THE CIOCH 1 96 1 LIST OF ILLUSTRATIONS Toface page SLIGACHAN BRIDGE, SGURR NAN GILLEAN AND THE bhasteir group . Frontispiece BEN CRUACHAN, FROM NEAR DALMALLY . 4 LOCH AN EILEAN ....... 9 AMONG THE CAIRNGORMS ; THE LARIG GHRU IN THE DISTANCE . -31 VIEW OF SKYE, FROM NEAR KYLE OF LOCH ALSH . -
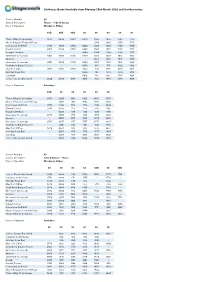
Caithness Guide Timetable from Monday 23Rd March 2020 Until Further Notice
Caithness Guide timetable from Monday 23rd March 2020 until further notice. Service Number 80 Service Description Thurso - John O Groats Days of Operation Monday to Friday 80D 80D 80D 80 80 80 80 80 Thurso Olrig St Santander 0551 0608 0640 0830 1025 1235 1545 1735 Mount Pleasant Towerhill Road - - - - 1030 1240 1550 1740 Castletown Drill Hall 0601 0618 0650 0840 1039 1249 1559 1749 Dunnet Corner 0607 0624 0656 0846 1045 1255 1605 1755 Brough Letterbox - - - 0849 1048 1258 1608 1758 Greenvale Crossroads 0611 0628 0700 0854 1053 1303 1613 1803 Barrock - - - - 1055 1305 1616 1806 Greenvale Crossroads 0611 0628 0700 0854 1057 1307 1618 1808 Scarfskerry Baptist Church - - - 0858 1101 1311 1622 1812 Mey Post Office 0615 0632 0704 904 1107 1317 1628 1818 Gills Bay Road End - - - 0909 1113 1323 1634 1824 Canisbay - - - 0912 1117 1327 1638 1828 John o' Groats Bus Stand 0626 0643 0715 0918 1124 1334 1645 1835 Days of Operation Saturdays 80D 80 80 80 80 80 Thurso Olrig St Santander 0725 0905 1105 1305 1505 1755 Mount Pleasant Towerhill Road - 0910 1110 1310 1510 1800 Castletown Drill Hall 0735 0919 1119 1319 1519 1809 Dunnet Corner 0741 0925 1125 1325 1525 1815 Brough Letterbox - 0928 1128 1328 1528 1818 Greenvale Crossroads 0745 0933 1133 1333 1533 1823 Barrock - 0935 1135 1335 1535 1825 Greenvale Crossroads 0745 0937 1137 1337 1537 1827 Scarfskerry Baptist Church - 0941 1141 1341 1541 1831 Mey Post Office 0749 0947 1147 1347 1547 1837 Gills Bay Road End - 0953 1153 1353 1553 1843 Canisbay - 0957 1157 1357 1557 1847 John o' Groats Bus Stand - 1004 -

Gaelic Scotland in the Colonial Imagination
Gaelic Scotland in the Colonial Imagination Gaelic Scotland in the Colonial Imagination Anglophone Writing from 1600 to 1900 Silke Stroh northwestern university press evanston, illinois Northwestern University Press www .nupress.northwestern .edu Copyright © 2017 by Northwestern University Press. Published 2017. All rights reserved. Printed in the United States of America 10 9 8 7 6 5 4 3 2 1 Library of Congress Cataloging-in-Publication data are available from the Library of Congress. Except where otherwise noted, this book is licensed under a Creative Commons At- tribution-NonCommercial-NoDerivatives 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. In all cases attribution should include the following information: Stroh, Silke. Gaelic Scotland in the Colonial Imagination: Anglophone Writing from 1600 to 1900. Evanston, Ill.: Northwestern University Press, 2017. For permissions beyond the scope of this license, visit www.nupress.northwestern.edu An electronic version of this book is freely available, thanks to the support of libraries working with Knowledge Unlatched. KU is a collaborative initiative designed to make high-quality books open access for the public good. More information about the initiative and links to the open-access version can be found at www.knowledgeunlatched.org Contents Acknowledgments vii Introduction 3 Chapter 1 The Modern Nation- State and Its Others: Civilizing Missions at Home and Abroad, ca. 1600 to 1800 33 Chapter 2 Anglophone Literature of Civilization and the Hybridized Gaelic Subject: Martin Martin’s Travel Writings 77 Chapter 3 The Reemergence of the Primitive Other? Noble Savagery and the Romantic Age 113 Chapter 4 From Flirtations with Romantic Otherness to a More Integrated National Synthesis: “Gentleman Savages” in Walter Scott’s Novel Waverley 141 Chapter 5 Of Celts and Teutons: Racial Biology and Anti- Gaelic Discourse, ca. -

<I>Actitis Hypoleucos</I>
Partial primary moult in first-spring/summer Common Sandpipers Actitis hypoleucos M. NICOLL 1 & P. KEMP 2 •c/o DundeeMuseum, Dundee, Tayside, UK 243 LochinverCrescent, Dundee, Tayside, UK Citation: Nicoll, M. & Kemp, P. 1983. Partial primary moult in first-spring/summer Common Sandpipers Actitis hypoleucos. Wader Study Group Bull. 37: 37-38. This note is intended to draw the attention of wader catch- and the old inner feathersare often retained (Pearson 1974). ers to the needfor carefulexamination of the primariesof Similarly, in Zimbabwe, first-year Common Sandpipers CommonSandpipers Actiris hypoleucos,and other waders, replacethe outerfive to sevenprimaries between December for partial primarywing moult. This is thoughtto be a diag- andApril (Tree 1974). It thusseems normal for first-spring/ nosticfeature of wadersin their first spring and summer summerCommon Sandpipers wintering in eastand southern (Tree 1974). Africa to show a contrast between new outer and old inner While membersof the Tay Ringing Group were mist- primaries.There is no informationfor birdswintering further nettingin Angus,Scotland, during early May 1980,a Com- north.However, there may be differencesin moult strategy mon Sandpiperdied accidentally.This bird was examined betweenwintering areas,since 3 of 23 juvenile Common and measured, noted as an adult, and then stored frozen un- Sandpiperscaught during autumn in Morocco had well- til it was skinned,'sexed', andthe gut contentsremoved for advancedprimary moult (Pienkowski et al. 1976). These analysis.Only duringskinning did we noticethat the outer birdswere moultingnormally, and so may have completed primarieswere fresh and unworn in comparisonto the faded a full primary moult during their first winter (M.W. Pien- and abradedinner primaries.The moult on both wingswas kowski, pers.comm.).