DOCSLIB.ORG

MATH 1325 – BUSINESS CALCULUS Section 10.2 Applications of the Second Derivative

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MATH 1325 – BUSINESS CALCULUS Section 10.2 Applications of the Second Derivative MATH 1325 – BUSINESS CALCULUS Section 10.2 Applications of the Second Derivative 00 What does f say about f ? Definition: Let f be differentiable on (a;b). 0 The graph of a function, f , is concave upward on the interval (a;b) if f (x) is increasing on (a;b). (If the graph of f lies above all of its tangents on an interval (a;b)) 0 The graph of a function, f , is concave downward on the interval (a;b) if f (x) is decreasing on (a;b). (If the graph of f lies below all of its tangents on an interval (a;b)) Concavity Test (a). If f 00(x) > 0 for all x in (a;b), then f is concave upward on (a;b). (b). If f 00(x) < 0 for all x in (a;b), then f is concave downward on (a;b). A change in concavity has a special name. Definition: A point P on a curve y = f (x) is called if f is continuous there and the curve changes from CU to CD or from CD to CU there. How do we find inflection points? 1. 2. 3. Math 1325 Section 10.2 Continued Ex: Find the intervals where the graph of f (x) = 4x3 + 3x2 − 6x + 1 is concave up, concave down and the inflection points. Then graph. Recall (from Section 10.1): 2 Math 1325 Section 10.2 Continued Ex: Find the intervals where the graph of g(x) = x2 + ln(x2) is concave up, concave down and the inflection points. HINT: Don’t forget about domain! The Second Derivative Test: 1. Compute f 0(x) and f 00(x). 2. Find all critical numbers of f at which f 0(x) = 0. 3. Compute f 00(c) for each critical number found in Step 2. (a) If f 00(c) < 0, then f has a relative maximum at c. (b) If f 00(c) > 0, then f has a relative minimum at c. (c) If f 00(c) = 0 or f 00(c) does not exist, then the test fails. (Inconclusive.) 3 Math 1325 Section 10.2 Continued Ex: Confirm the local extrema for f (x) = 4x3 + 3x2 − 6x + 1 by using the Second Derivative Test. Ex: Find the local extrema for g(x) = ln(x2 + 1) by using the Second Derivative Test. SUMMARY: Signs of f and f 0 Properties of f General Shape of Graph of f f 0(x) > 0 f is increasing f 00(x) > 0 Graph of f is CU f 0(x) > 0 f is increasing f 00(x) < 0 Graph of f is CD f 0(x) < 0 f is decreasing f 00(x) > 0 Graph of f is CU f 0(x) < 0 f is decreasing f 00(x) < 0 Graph of f is CD 4 Math 1325 Section 10.2 Continued Ex: Congress created the alternative minimum tax (AMT) in the late 1970s to ensure that wealthy people paid their fair share of taxes. But because of quirks in the law, even middle-income taxpayers have started to get hit with the tax. The AMT (in billions of dollars) projected to be collected by the IRS from 2001 through 2010 is f (t) = 0:0117t3 + 0:0037t2 + 0:7563t + 4:1 (0 ≤ t ≤ 9) where t is measured in years, with t = 0 corresponding to 2001. (a) Show that f is increasing on the interval (0;9). (b) What does this result tell you about the projected amount of AMT paid over the years in question? (c) Show that f is increasing on the interval (0;9). (d) What conclusion can you draw from this result concerning the rate of growth of the amount of AMT collected over the years in question? 5 Math 1325 Section 10.2 Continued If a company spends money on advertising, the hope is that sales will increase. Sales will increase, rapidly at first, but then the rate of increase will begin to increase less rapidly. This is when the sales are at a maximum value and the function has a point of inflection. This point is called the point of diminishing returns. Ex: An appliance store is selling dryers and decides to invest x thousand in advertising. It estimates that sales can be modeled by the function N(x) = 3x3 − 0:25x2 + 200 (0 ≤ x ≤ 9) NOTE: N0(x) = 9x2 − x3 and N00(x) = 18x − 3x2 N0(x) has a maximum at x = N(x) has an inflection point at x = . The point of diminishing returns is x = . Thus, the rate of change of sales begins to decrease when $ is spent on advertising. 6.
Load more

Recommended publications
  • Chapter 9 Optimization: One Choice Variable
    RS - Ch 9 - Optimization: One Variable Chapter 9 Optimization: One Choice Variable 1 Léon Walras (1834-1910) Vilfredo Federico D. Pareto (1848–1923) 9.1 Optimum Values and Extreme Values • Goal vs. non-goal equilibrium • In the optimization process, we need to identify the objective function to optimize. • In the objective function the dependent variable represents the object of maximization or minimization Example: - Define profit function: = PQ − C(Q) - Objective: Maximize - Tool: Q 2 1 RS - Ch 9 - Optimization: One Variable 9.2 Relative Maximum and Minimum: First- Derivative Test Critical Value The critical value of x is the value x0 if f ′(x0)= 0. • A stationary value of y is f(x0). • A stationary point is the point with coordinates x0 and f(x0). • A stationary point is coordinate of the extremum. • Theorem (Weierstrass) Let f : S→R be a real-valued function defined on a compact (bounded and closed) set S ∈ Rn. If f is continuous on S, then f attains its maximum and minimum values on S. That is, there exists a point c1 and c2 such that f (c1) ≤ f (x) ≤ f (c2) ∀x ∈ S. 3 9.2 First-derivative test •The first-order condition (f.o.c.) or necessary condition for extrema is that f '(x*) = 0 and the value of f(x*) is: • A relative minimum if f '(x*) changes its sign y from negative to positive from the B immediate left of x0 to its immediate right. f '(x*)=0 (first derivative test of min.) x x* y • A relative maximum if the derivative f '(x) A f '(x*) = 0 changes its sign from positive to negative from the immediate left of the point x* to its immediate right.
    [Show full text]
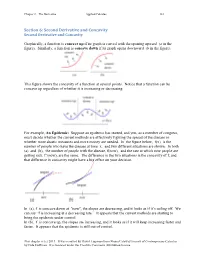
  • Section 6: Second Derivative and Concavity Second Derivative and Concavity
    Chapter 2 The Derivative Applied Calculus 122 Section 6: Second Derivative and Concavity Second Derivative and Concavity Graphically, a function is concave up if its graph is curved with the opening upward (a in the figure). Similarly, a function is concave down if its graph opens downward (b in the figure). This figure shows the concavity of a function at several points. Notice that a function can be concave up regardless of whether it is increasing or decreasing. For example, An Epidemic: Suppose an epidemic has started, and you, as a member of congress, must decide whether the current methods are effectively fighting the spread of the disease or whether more drastic measures and more money are needed. In the figure below, f(x) is the number of people who have the disease at time x, and two different situations are shown. In both (a) and (b), the number of people with the disease, f(now), and the rate at which new people are getting sick, f '(now), are the same. The difference in the two situations is the concavity of f, and that difference in concavity might have a big effect on your decision. In (a), f is concave down at "now", the slopes are decreasing, and it looks as if it’s tailing off. We can say “f is increasing at a decreasing rate.” It appears that the current methods are starting to bring the epidemic under control. In (b), f is concave up, the slopes are increasing, and it looks as if it will keep increasing faster and faster.
    [Show full text]
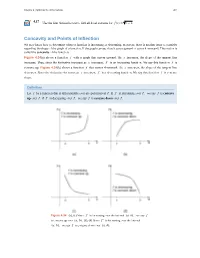
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Chapter 8 Optimal Points
    Samenvatting Essential Mathematics for Economics Analysis 14-15 Chapter 8 Optimal Points Extreme points The extreme points of a function are where it reaches its largest and its smallest values, the maximum and minimum points. Formally, • is the maximum point for for all • is the minimum point for for all Where the derivative of the function equals zero, , the point x is called a stationary point or critical point . For some point to be the maximum or minimum of a function, it has to be such a stationary point. This is called the first-order condition . It is a necessary condition for a differentiable function to have a maximum of minimum at a point in its domain. Stationary points can be local or global maxima or minima, or an inflection point. We can find the nature of stationary points by using the first derivative. The following logic should hold: • If for and for , then is the maximum point for . • If for and for , then is the minimum point for . Is a function concave on a certain interval I, then the stationary point in this interval is a maximum point for the function. When it is a convex function, the stationary point is a minimum. Economic Applications Take the following example, when the price of a product is p, the revenue can be found by . What price maximizes the revenue? 1. Find the first derivative: 2. Set the first derivative equal to zero, , and solve for p. 3. The result is . Before we can conclude whether revenue is maximized at 2, we need to check whether 2 is indeed a maximum point.
    [Show full text]
  • Concavity and Inflection Points. Extreme Values and the Second
    Calculus 1 Lia Vas Concavity and Inflection Points. Extreme Values and The Second Derivative Test. Consider the following two increasing functions. While they are both increasing, their concavity distinguishes them. The first function is said to be concave up and the second to be concave down. More generally, a function is said to be concave up on an interval if the graph of the function is above the tangent at each point of the interval. A function is said to be concave down on an interval if the graph of the function is below the tangent at each point of the interval. Concave up Concave down In case of the two functions above, their concavity relates to the rate of the increase. While the first derivative of both functions is positive since both are increasing, the rate of the increase distinguishes them. The first function increases at an increasing rate (see how the tangents become steeper as x-values increase) because the slope of the tangent line becomes steeper and steeper as x values increase. So, the first derivative of the first function is increasing. Thus, the derivative of the first derivative, the second derivative is positive. Note that this function is concave up. The second function increases at an decreasing rate (see how it flattens towards the right end of the graph) so that the first derivative of the second function is decreasing because the slope of the 1 tangent line becomes less and less steep as x values increase. So, the derivative of the first derivative, second derivative is negative.
    [Show full text]
  • 1 Objective 2 Roots, Peaks and Troughs, Inflection Points
    BEE1020 { Basic Mathematical Economics Dieter Balkenborg Week 9, Lecture Wednesday 04.12.02 Department of Economics Discussing graphs of functions University of Exeter 1Objective We show how the ¯rst and the second derivative of a function can be used to describe the qualitative properties of its graph. This will be used in the next lecture to solve optimization problems. 2 Roots, peaks and troughs, in°ection points 2.1 Roots: f (x)=0 A solution to the equation f (x)=0wheref is a function is called a root or x-intercept. At a root the function may or may not switch sign. In the ¯gure on the left the function the function has a root at x = 1and switches sign there. In the ¯gure on the right the function has a root at x = 1,¡ but does not switch sign there. ¡ 8 6 3 4 2 0 -2 -1x 1 2 -2 1 -4 -6 0 -2 -1x 1 2 f (x)=x3 +1 f (x)=x2 4 10 2 8 6 0 -2 -1x 1 2 4 -2 2 -4 0 -2 -1x 1 2 2 f 0 (x)=3x f 0 (x)=2x Lemma 1 Suppose the function y = f (x) is di®erentiable on the interval a x b with · · a<b.Supposex0 with a<x0 <bisarootoftheafunctionandf 0 (x0) =0.Thenthe 6 function switches sign at x0 2.2 Critical points: f 0 (x)=0 A solution to the equation f 0 (x)=0,wheref 0 is the ¯rst derivative of a function f,is called a critical point or a stationary point of the function f.
    [Show full text]
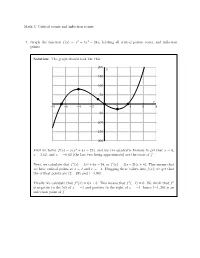
  • Critical Points and Inflection Points 1. Graph the Function F(X) = X 3 +
    Math 3: Critical points and inflection points 1. Graph the function f(x) = x3 + 3x2 − 24x, labeling all critical points, roots, and inflection points. Solution: The graph should look like this: 200 y 150 100 50 x −8 −6 −4 −2 2 4 6 8 −50 −100 −150 −200 First we factor f(x) = x(x2 + 3x − 24), and use the quadratic formula to get that x = 0, x = 3:62, and x = −6:62 (the last two being approximate) are the roots of f. Next, we calculate that f 0(x) = 3x2 + 6x − 24, or f 0(x) = 3(x − 2)(x + 4). This means that we have critical points at x = 2 and x = −4. Plugging these values into f(x), we get that the critical points are (2; −28) and (−4; 80). Finally, we calculate that f 00(x) = 6x + 6. This means that f 00(−1) = 0. We check that f 00 is negative to the left of x = −1 and positive to the right of x = −1, hence (−1; 26) is an inflection point of f. 1 2. Let f(x) = sin(x) − 2 x. Find all critical points of f and determine whether each critical point is a local maximum, a local minimum, or neither. Also find all points of inflection of f. 0 1 1 Solution: We have that f (x) = cos(x)− 2 , hence the critical points occur when cos(x) = 2 . π π This happens when x = 3 + 2πn or x = − 3 + 2πn, where n is any integer. To determine the behavior at these points, we could use the first derivative test, but in this case the second derivative test is easier.
    [Show full text]
  • Saddle Points and Inflection Points
    ( ) ( ) − f k h . lim 2 f k 1 h→0 2 f (h) − f (0) Since f is continuous by hypothesis, it follows that this limit is indeed f (0). In the case when the function is a parabola, a calculation shows that, for fixed h,the area of ABP is constant even as the point a varies (see Figure 2). This geometric curiosity may well have been known to the ancient Greeks of course. What about the converse question: for which functions is Area(a, h) independent of a?Thetheorem we just proved provides an answer to that: only parabolas (and lines, in which case all the triangles are degenerate and the areas vanish). Figure 2. Corollary. Let f have a continuous non-zero second derivative on an open interval I . If, for all x in I , Area(x, h) depends only on h, then the graph of f is a parabola, and conversely. Acknowledgment. The author wishes to thank the referee for several suggested improvements. References 1. W. Rudin, Principles of Mathematical Analysis, 3rd ed., McGraw-Hill, 1976. ◦ Saddle Points and Inflection Points Felix´ Mart´ınez de la Rosa ([email protected]), Universidad de Cadiz,´ Cadiz,´ Spain. In the study of surfaces in multivariate calculus, we notice some similarities be- tween saddle points on surfaces and inflection points on curves. In this note, we make a direct connection between the two concepts. Throughout, we assume that f (x, y) has continuous second partial derivatives in an open set in the plane, and that (a, b) is a critical point in that set (that is, fx (a, b) = fy(a, b) = 0).
    [Show full text]
  • Inflection Points in Families of Algebraic Curves
    Inflection Points in Families of Algebraic Curves Ashvin A. Swaminathan Harvard College A thesis submitted for the degree of Artium Baccalaureus in Mathematics, with Honors March 2017 Advised by Joseph D. Harris and Anand P. Patel Abstract In this thesis, we discuss the theory of inflection points of algebraic curves from the perspective of enumerative geometry. The standard technique for counting inflection points — namely, computing Chern classes of the sheaves of principal parts — works quite well over smooth curves, but difficulties arise over singular curves. Our main results constitute a new approach to dealing with the problem of counting inflection points in one-parameter families of curves that have singular members. In the context of such families, we introduce a system of sheaves that serves to replace the sheaves of principal parts. The Chern classes of the new sheaves can be expressed as a main term plus error terms, with the main term arising from honest inflection points and the error terms arising from singular points. We explicitly compute the error term associated with a nodal singularity, and as a corollary, we deduce a lower bound on the error terms arising from other types of planar singularities. Our results can be used to answer a broad range of questions, from counting hyperflexes in a pencil of plane curves, to determining the analytic-local behavior of inflection points in a family of plane curves specializing to a singular curve, to computing the divisors of higher- order Weierstrass points in the moduli space of curves. Acknowledgements To begin with, I thank my advisor, Joe Harris, for suggesting the questions that led to this thesis and for providing me with the best guidance that I could have ever hoped for.
    [Show full text]
  • RADIUS of CURVATURE and EVOLUTE of the FUNCTION Y=F(X)
    RADIUS OF CURVATURE AND EVOLUTE OF THE FUNCTION y=f(x) In introductory calculus one learns about the curvature of a function y=f(x) and also about the path (evolute) that the center of curvature traces out as x is varied along the original curve. Beginning students sometimes have difficulty in deriving and understanding the quantity [1+(df/dx)2]3/2which enters such calculations. We want here to review these concepts and add a few simplifying thoughts which will help clarify the problem. We start with a continuous curve y=f(x) as shown – An increment of length ds along this curve is- df ds dx 2 dy 2 dx 1 ( )2 dx Also we have that at x the angle between the x axis and the curve is- dy arctan( ) arctan[ f '(x)] dx Differentiating this last expression with respect to x produces- f "(x) d dx [1 f '(x)2 ] If we now go back to the above figure, we see that at any point x along the curve y=f(x) there lies a unique circle whose radius represents the radius of curvature r=. Mathematically we have- ds dx 1 f '(x)2 [1 f '(x)2 ]3/ 2 | | d { f "(x)dx /[ 1 f '(x)2 ] f "(x) The absolute value symbol has been added because should always be considered a positive quantity. Notice this radius of curvature is just the reciprocal of standard curvature, usually, designated by K. The curvature of f(x) changes sign as one passes through an inflection point where f ”(x)=0.
    [Show full text]
  • Inflection Points and Asymptotic Lines on Lagrangean Surfaces
    INFLECTION POINTS AND ASYMPTOTIC LINES ON LAGRANGEAN SURFACES J. BASTO-GONC¸ALVES Abstract. We describe the structure of the asymptotic lines near an inflection point of a Lagrangean surface, proving that in the generic situation it corresponds to two of the three possible cases when the discriminant curve has a cusp singularity. Besides being stable in general, inflection points are proved to exist on a com- pact Lagrangean surface whenever its Euler characteristic does not vanish. 1. Introduction The origin of the study of surfaces in R4 was the interpretation of a complex plane curve as a real surface. This is very natural, as formulae for curves in the real plane, curvature for instance, can be adapted to complex curves and then seen again in a real version but for surfaces in R4. In a different context, an invariant torus for a two degrees of freedom integrable Hamiltonian system is also a Lagrangean surface in R4, and in general Lagrangean surfaces play an important role for 4-dimensional symplectic manifolds. In particular, the real version of plane complex curves are always Lagrangean surfaces for a suitable symplectic form. From the point of view of singularity theory, and after the generic points, the first interesting points are inflection points. We follow a similar approach here, along the lines of [8] and [10, 7], and consider the generic situation for inflection points in Lagrangean surfaces: the normal form at those points and thestructure of the asymptotic lines around them. The generic picture for Lagrangean surfaces is quite different from that for arbitrary generic surfaces in R4: we prove that all inflection points are flat inflection points (this is a codimension one situation in general), and that there are two possible (topological) phase portraits for the asymptotic lines around an inflection point, corresponding to Date: July 31, 2013.
    [Show full text]