DOCSLIB.ORG

University Students' Grasp of Inflection Points

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
University Students' Grasp of Inflection Points Educ Stud Math DOI 10.1007/s10649-012-9463-1 University students’ grasp of inflection points Pessia Tsamir & Regina Ovodenko # Springer Science+Business Media Dordrecht 2013 Abstract This paper describes university students’ grasp of inflection points. The participants were asked what inflection points are, to mark inflection points on graphs, to judge the validity of related statements, and to find inflection points by investigating (1) a function, (2) the derivative, and (3) the graph of the derivative. We found four erroneous images of inflection points: (1) f ′ (x)=0 as a necessary condition, (2) f ′ (x)≠0 as a necessary condition, (3) f ″ (x)=0 as a sufficient condition, and (4) the location of “a peak point, where the graph bends” as an inflection point. We use the lenses of Fischbein, Tall, and Vinner and Duval’s frameworks to analyze students’ errors that were rooted in mathematical and in real-life contexts. Keywords Inflection point . Concept image . Representation . Definition . Intuition 1 Introduction The notion of inflection points is frequently discussed when dealing with investigations of functions in calculus. Calculus is an important domain in mathematics and a central subject within high school and post-high school mathematics curricula. In the literature and in our preliminary studies, we found a few indications of learners’ erroneous conceptions of the notion (e.g., Ovodenko & Tsamir, 2005; Tall, 1987; Vinner, 1982). While the findings shed some light on students’ grasp of inflection points, it seems important to further investigate students’ related conceptions and to examine potential sources for their common errors. In this paper, we examine university students’ conceptions of the notion of inflection points, and we also use the context of inflection points to examine students’ proofs (validating and refuting) when addressing inflection-point-related statements. In the field of mathematics education, there are several theoretical frameworks proposing ways to analyze students’ mathematical reasoning; yet usually, research data are interpreted in light of a single theory. We believe that the use of different lenses may contribute to our interpretational examinations of the data and may offer us rich terminologies to address and to analyze the findings (e.g., Tsamir, 2007, 2008). Thus, we offer a range of interpretations of students’ conceptions based on three theoretical frameworks which are widely used to highlight possible sources of students’ difficulties in mathematics: Fischbein’s(e.g.,1993a) analyses of P. Tsamir (*) : R. Ovodenko Tel Aviv University, Tel Aviv, Israel e-mail: [email protected] P. Tsamir, R. Ovodenko learners’ intuitive algorithmic and formal knowledge; Tall and Vinner’s(e.g.,1981) review of concept image and concept definition; and Duval’s(e.g.,2006) investigations of the role of representation and visualization in students’ (in)comprehension of mathematics. 2 Theoretical framework In this section, we first survey the literature regarding: “What does research tell us about students’ conceptions of inflection points?” Then, we attend to the question: “What are possible sources of students’ mathematical errors?” 2.1 What does research tell us about students’ conceptions of inflection points? In the literature, there are some indications of difficulties that students encounter when using the notion of inflection points. For example, studies on students’ performances on connec- tions between functions and their derivatives within realistic contexts reported that students tend to err when identifying or when representing inflection points on graphs (e.g., Monk, 1992; Nemirovsky & Rubin, 1992; Carlson, Jacobs, Coe, Larsen & Hsu, 2002). Students also tend to use fragments of phrases taken from earlier-learnt theorems, such as: “if the second derivative equals zero [then] inflection point” even when solving problems in the context of “dynamic real-world situation” (Carlson et al., 2002, p. 355). On this matter, Nardi reported in her book: Amongst mathematicians: Teaching and learning mathematics at university level that “there is the classic example from school mathematics: how the second derivative being zero at a point implying the point being an inflection point” (Nardi, 2008,p.66).Aninteresting,relatedpieceofevidencewasfoundinMason’s(2001) reflection on his past engagement (as an undergraduate) with the task: “Do y=x5 and y=x6 have points of inflection? How do you know?” Mason recalled being familiar with the shapes of y=x5 and y=x6, thus knowing immediately which does and which does not have an inflection point. Still, he clearly remembered being perplexed when reaching in both cases, f ″ (x)=0 at x=0, and wondering why is it that one has an inflection and the other not? These data indicate that even future mathematicians may experience (as undergraduates) intuitive unease when encountering the insufficiency of f ″ (x)=0 for an inflection point. Gomez and Carulla (2001) reported on students’ grasp of connections between the location of inflection points and the location of the graph related to the axes. Students claimed that, if an inflection point of y=f (x) is on the y-axis or “close enough” to it, then the graph crosses that axis; if an inflection point is “not close, yet not too far from the y-axis,” then the y-axis is an asymptote of the graph; if an inflection point is “far enough from the y- axis,” then the graph has other asymptotes; and if the inflection point “is far enough from x- axis,” then it does not cross that axis. Another line of research on students’ conceptions of inflection points addressed issues related to the tangent at such points (e.g., Artigue, 1992; Vinner, 1982; 1991; Tall, 1987). For instance, Vinner (1982) reported that early experiences of the tangent of circles led learners to believe that “the tangent is a line that touches the graph at one point and does not cross the graph” (see also Artigue, 1992; Tall, 1987). In an early study, we examined university students’ conceptions of inflection points. We came across a novel tendency to regard a “peak or bending point” (i.e., a point where the graph keeps increasing or decreasing but dramatically changes the rate of change) as an inflection point (Tsamir & Ovodenko, 2004). We also found tendencies to regard f ′ (x0)=0 necessary for the existence of an inflection point at x=x0 (Ovodenko & Tsamir, 2005); and we observed that different erroneous conceptions of inflection points evolve when students University students’ grasp of inflection points address a variety of tasks. Thus, we instigated another study to examine university students’ conceptions when solving problems that offer rich opportunities to address inflection points. We report here on the findings. 2.2 What are possible sources of students’ mathematical errors? The analysis of students’ common errors calls for the use of related theoretical frameworks. Usually, studies on students’ conceptions use one interpretational framework to shed light on the data. We enriched our scope of analysis by using the perspectives offered by Fischbein (e.g., 1987), Tall and Vinner (e.g., 1981), and Duval (e.g., 2006) that were widely used by mathematics education researchers for analyzing students’ common errors and for examin- ing possible related sources. Fischbein (e.g., 1987, 1993b) claimed that students’ mathematical performances include three basic aspects: the algorithmic aspect, i.e., knowledge of rules, processes, and ways to apply them in a solution, and knowledge of “why” each of the steps in the algorithm is correct; the formal aspect, i.e., knowledge of axioms, definitions, theorems, proofs, and knowledge of how the mathematical realm works (e.g., consistency); and the intuitive aspect that was characterized as immediate, confident, and obviously grasped as correct although it is not necessarily so. Fischbein explained that, while neither formal knowledge nor algo- rithmic knowledge are spontaneously acquired, intuitive knowledge develops as an effect of learners’ personal experience, independent of any systematic instruction. Sometimes, intu- itive ideas hinder formal interpretations or algorithmic procedures and cause erroneous, rigid algorithmic methods, which were labeled algorithmic models. For example, students’ tendencies to claim that (a+b)5=a5+b5 or sin(α+β)=sin α+sin β were interpreted as evolving from the application of the distributive law (Fischbein, 1993a). Fischbein’s analysis of students’ intuitive grasp of geometrical and graphs-related notions led him to coin the term figural concepts, i.e., mental, spatial images, handled by geometrical or functions-based reasoning. Figural concepts may become autonomous, free of formal control, and thus erroneous (Fischbein, 1993a). Fischbein noted that a certain interpretation of a concept may initially be useful in the teaching process due to its intuitive qualities and its local concreteness. But, as a result of the primacy effect, this initial model may become rigidly attached to the concept and generate obstacles to advanced interpretations of the concept. Fischbein’s framework was widely used to analyze students’ mathematical conceptions of various notions, such as functions, infinity, limit, and sets (e.g., Fischbein, 1987). Two other researchers who examined learners’ grasp of mathematical notions are Tall and Vinner (e.g., 1981) who coined the terms concept-image and concept-definition. Concept image includes all the mental pictures and the properties that a person associates with
Load more

Recommended publications
  • Representation of Inflected Nouns in the Internal Lexicon
    Memory & Cognition 1980, Vol. 8 (5), 415423 Represeritation of inflected nouns in the internal lexicon G. LUKATELA, B. GLIGORIJEVIC, and A. KOSTIC University ofBelgrade, Belgrade, Yugoslavia and M.T.TURVEY University ofConnecticut, Storrs, Connecticut 06268 and Haskins Laboratories, New Haven, Connecticut 06510 The lexical representation of Serbo-Croatian nouns was investigated in a lexical decision task. Because Serbo-Croatian nouns are declined, a noun may appear in one of several gram­ matical cases distinguished by the inflectional morpheme affixed to the base form. The gram­ matical cases occur with different frequencies, although some are visually and phonetically identical. When the frequencies of identical forms are compounded, the ordering of frequencies is not the same for masculine and feminine genders. These two genders are distinguished further by the fact that the base form for masculine nouns is an actual grammatical case, the nominative singular, whereas the base form for feminine nouns is an abstraction in that it cannot stand alone as an independent word. Exploiting these characteristics of the Serbo­ Croatian language, we contrasted three views of how a noun is represented: (1) the independent­ entries hypothesis, which assumes an independent representation for each grammatical case, reflecting its frequency of occurrence; (2) the derivational hypothesis, which assumes that only the base morpheme is stored, with the individual cases derived from separately stored inflec­ tional morphemes and rules for combination; and (3) the satellite-entries hypothesis, which assumes that all cases are individually represented, with the nominative singular functioning as the nucleus and the embodiment of the noun's frequency and around which the other cases cluster uniformly.
    [Show full text]
  • Who, Whom, Whoever, and Whomever
    San José State University Writing Center www.sjsu.edu/writingcenter Written by Cassia Homann Who, Whom, Whoever, and Whomever People often do not know when to use the pronouns “who,” “whom,” “whoever,” and “whomever.” However, with a simple trick, they will always choose the correct pronoun. For this trick, use the following key: who = she, he, I, they whom = her, him, me, them Who In the following sentences, use the steps that are outlined to decide whether to use who or whom. Example Nicole is a girl (who/whom) likes to read. Step 1: Cover up the part of the sentence before “who/whom.” Nicole is a girl (who/whom) likes to read. Step 2: For the remaining part of the sentence, test with a pronoun using the above key. Replace “who” with “she”; replace “whom” with “her.” Who likes to read = She likes to read Whom likes to read = Her likes to read Step 3: Consider which one sounds correct. (Remember that the pronoun “she” is the subject of a sentence, and the pronoun “her” is part of the object of a sentence.) “She likes to read” is the correct wording. Step 4: Because “she” works, the correct pronoun to use is “who.” Nicole is a girl who likes to read. Who, Whom, Whoever, and Whomever, Fall 2012. Rev. Summer 2014. 1 of 4 Whom Example Elizabeth wrote a letter to someone (who/whom) she had never met. Step 1: Cover up the part of the sentence before “who/whom.” Elizabeth wrote a letter to someone (who/whom) she had never met.
    [Show full text]
  • Case Management and Staff Support Across NCI States
    What the 2018-19 NCI® Child Family Survey data tells us about Case Management and Staff Support Across NCI States This report tells us about: • What NCI tells us about case management and staff support • Why this is important What is NCI? Each year, NCI asks people with intellectual and developmental disabilities (IDD) and their families how they feel about their lives and the services they get. NCI uses surveys so that the same questions can be asked to people in all NCI states. Who answered questions to this survey? Questions for this survey are answered by a person who lives in the same house as a child who is getting services from the state. Most of the time, a parent answers these questions. Sometimes a sibling or someone who lives with the child and knows them well answers these questions. 2 How are data shown in this report? NCI asks questions about planning services and supports for children who get services from the state. In this report we see how family members of children getting services answered questions about planning services and supports. • In this report, when we say “you” we mean the person who is answering the question (most of the time, a parent). • In this report, when we say “child” we mean the child who is getting services from the state. 3 We use words and figures to show the number of yes and no answers we got. Some of our survey questions have more than a yes or no answer. They ask people to pick: “always,” “usually,” “sometimes,” or “seldom/never.” For this report, we count all “always” answers as yes.
    [Show full text]
  • The Function of Phrasal Verbs and Their Lexical Counterparts in Technical Manuals
    Portland State University PDXScholar Dissertations and Theses Dissertations and Theses 1991 The function of phrasal verbs and their lexical counterparts in technical manuals Brock Brady Portland State University Follow this and additional works at: https://pdxscholar.library.pdx.edu/open_access_etds Part of the Applied Linguistics Commons Let us know how access to this document benefits ou.y Recommended Citation Brady, Brock, "The function of phrasal verbs and their lexical counterparts in technical manuals" (1991). Dissertations and Theses. Paper 4181. https://doi.org/10.15760/etd.6065 This Thesis is brought to you for free and open access. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. AN ABSTRACT OF THE THESIS OF Brock Brady for the Master of Arts in Teaching English to Speakers of Other Languages (lESOL) presented March 29th, 1991. Title: The Function of Phrasal Verbs and their Lexical Counterparts in Technical Manuals APPROVED BY THE MEMBERS OF THE THESIS COMMITTEE: { e.!I :flette S. DeCarrico, Chair Marjorie Terdal Thomas Dieterich Sister Rita Rose Vistica This study investigates the use of phrasal verbs and their lexical counterparts (i.e. nouns with a lexical structure and meaning similar to corresponding phrasal verbs) in technical manuals from three perspectives: (1) that such two-word items might be more frequent in technical writing than in general texts; (2) that these two-word items might have particular functions in technical writing; and that (3) 2 frequencies of these items might vary according to the presumed expertise of the text's audience.
    [Show full text]
  • Grammar Worksheets: Who Or Whom?
    Grammar Worksheets: Who or Whom? http://www.grammar-worksheets.com People are so mystified (confused) about the use of who and whom that some of us are tempted to throw RXUKDQGVLQWKHDLUDQGVD\³LWMXVWGRHVQ¶WPDWWHU´%XWLWGRHVPDWWHU7KRVHZKRNQRZ DQGQRWMXVW English teachers), judge those who misuse it. Not using who and whom correctly can cost you, not just in schooOEXWDOVRLQOLIH/HW¶VJHWLWGRZQQRZ Who and Whom are Pronouns 7KDW¶VULJKW who and whom are pronouns. And if you recall, a pronoun is a word that takes the place of a noun. Sometimes we use pronouns instead of nouns. :HZRXOGQRWVD\³-HVVH GRHVQ¶WOLNHWKHSULQFLSDO0V7KRPDVZDVKLUHGDWKLVVFKRRO´7KHQDPHMs. Thomas LVDQRXQ)RUWKLVVHQWHQFHWRIORZZHZRXOGZULWH³-HVVHGRHVQ¶WOLNHWKHSULQFLSDOZKRZDV KLUHGDWKLVVFKRRO´ It All Depends on Case In English grammar, we have a term called case, which refers to pronouns. The case of a pronoun can be either subject or object, depending on its use in a sentence. Take a look at this table. Subject Object I me he him she her we us they them who whom The pronoun who is used as a subject; whom is used as an object. Who used correctly: Janice is the student who has read the most books. Whom used correctly: Janice is the student whom the teachers picked as outstanding. How Can I Determine Which One to Use? Break up the sentence into two parts. Janice is the student. She (Janice) has read the most books. Janice is the student. The teachers picked her (Janice) as outstanding. If you use I, he, she, we, or they, then the correct form is who. If you use me, him, her, us, or them, then the correct form is whom.
    [Show full text]
  • Verbal Case and the Nature of Polysynthetic Inflection
    Verbal case and the nature of polysynthetic inflection Colin Phillips MIT Abstract This paper tries to resolve a conflict in the literature on the connection between ‘rich’ agreement and argument-drop. Jelinek (1984) claims that inflectional affixes in polysynthetic languages are theta-role bearing arguments; Baker (1991) argues that such affixes are agreement, bearing Case but no theta-role. Evidence from Yimas shows that both of these views can be correct, within a single language. Explanation of what kind of inflection is used where also provides us with an account of the unusual split ergative agreement system of Yimas, and suggests a novel explanation for the ban on subject incorporation, and some exceptions to the ban. 1. Two types of inflection My main aim in this paper is to demonstrate that inflectional affixes can be very different kinds of syntactic objects, even within a single language. I illustrate this point with evidence from Yimas, a Papuan language of New Guinea (Foley 1991). Understanding of the nature of the different inflectional affixes of Yimas provides an explanation for its remarkably elaborate agreement system, which follows a basic split-ergative scheme, but with a number of added complications. Anticipating my conclusions, the structure in (1c) shows what I assume the four principal case affixes on a Yimas verb to be. What I refer to as Nominative and Accusative affixes are pronominal arguments: these inflections, which are restricted to 1st and 2nd person arguments in Yimas, begin as specifiers and complements of the verb, and incorporate into the verb by S- structure. On the other hand, what I refer to as Ergative and Absolutive inflection are genuine agreement - they are the spell-out of functional heads, above VP, which agree with an argument in their specifier.
    [Show full text]
  • Chapter 9 Optimization: One Choice Variable
    RS - Ch 9 - Optimization: One Variable Chapter 9 Optimization: One Choice Variable 1 Léon Walras (1834-1910) Vilfredo Federico D. Pareto (1848–1923) 9.1 Optimum Values and Extreme Values • Goal vs. non-goal equilibrium • In the optimization process, we need to identify the objective function to optimize. • In the objective function the dependent variable represents the object of maximization or minimization Example: - Define profit function: = PQ − C(Q) - Objective: Maximize - Tool: Q 2 1 RS - Ch 9 - Optimization: One Variable 9.2 Relative Maximum and Minimum: First- Derivative Test Critical Value The critical value of x is the value x0 if f ′(x0)= 0. • A stationary value of y is f(x0). • A stationary point is the point with coordinates x0 and f(x0). • A stationary point is coordinate of the extremum. • Theorem (Weierstrass) Let f : S→R be a real-valued function defined on a compact (bounded and closed) set S ∈ Rn. If f is continuous on S, then f attains its maximum and minimum values on S. That is, there exists a point c1 and c2 such that f (c1) ≤ f (x) ≤ f (c2) ∀x ∈ S. 3 9.2 First-derivative test •The first-order condition (f.o.c.) or necessary condition for extrema is that f '(x*) = 0 and the value of f(x*) is: • A relative minimum if f '(x*) changes its sign y from negative to positive from the B immediate left of x0 to its immediate right. f '(x*)=0 (first derivative test of min.) x x* y • A relative maximum if the derivative f '(x) A f '(x*) = 0 changes its sign from positive to negative from the immediate left of the point x* to its immediate right.
    [Show full text]
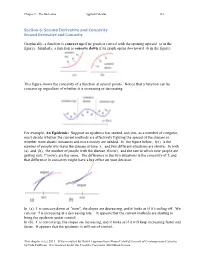
  • Section 6: Second Derivative and Concavity Second Derivative and Concavity
    Chapter 2 The Derivative Applied Calculus 122 Section 6: Second Derivative and Concavity Second Derivative and Concavity Graphically, a function is concave up if its graph is curved with the opening upward (a in the figure). Similarly, a function is concave down if its graph opens downward (b in the figure). This figure shows the concavity of a function at several points. Notice that a function can be concave up regardless of whether it is increasing or decreasing. For example, An Epidemic: Suppose an epidemic has started, and you, as a member of congress, must decide whether the current methods are effectively fighting the spread of the disease or whether more drastic measures and more money are needed. In the figure below, f(x) is the number of people who have the disease at time x, and two different situations are shown. In both (a) and (b), the number of people with the disease, f(now), and the rate at which new people are getting sick, f '(now), are the same. The difference in the two situations is the concavity of f, and that difference in concavity might have a big effect on your decision. In (a), f is concave down at "now", the slopes are decreasing, and it looks as if it’s tailing off. We can say “f is increasing at a decreasing rate.” It appears that the current methods are starting to bring the epidemic under control. In (b), f is concave up, the slopes are increasing, and it looks as if it will keep increasing faster and faster.
    [Show full text]
  • Serial Verb Constructions Revisited: a Case Study from Koro
    Serial Verb Constructions Revisited: A Case Study from Koro By Jessica Cleary-Kemp A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Linguistics in the Graduate Division of the University of California, Berkeley Committee in charge: Associate Professor Lev D. Michael, Chair Assistant Professor Peter S. Jenks Professor William F. Hanks Summer 2015 © Copyright by Jessica Cleary-Kemp All Rights Reserved Abstract Serial Verb Constructions Revisited: A Case Study from Koro by Jessica Cleary-Kemp Doctor of Philosophy in Linguistics University of California, Berkeley Associate Professor Lev D. Michael, Chair In this dissertation a methodology for identifying and analyzing serial verb constructions (SVCs) is developed, and its application is exemplified through an analysis of SVCs in Koro, an Oceanic language of Papua New Guinea. SVCs involve two main verbs that form a single predicate and share at least one of their arguments. In addition, they have shared values for tense, aspect, and mood, and they denote a single event. The unique syntactic and semantic properties of SVCs present a number of theoretical challenges, and thus they have invited great interest from syntacticians and typologists alike. But characterizing the nature of SVCs and making generalizations about the typology of serializing languages has proven difficult. There is still debate about both the surface properties of SVCs and their underlying syntactic structure. The current work addresses some of these issues by approaching serialization from two angles: the typological and the language-specific. On the typological front, it refines the definition of ‘SVC’ and develops a principled set of cross-linguistically applicable diagnostics.
    [Show full text]
  • The “Person” Category in the Zamuco Languages. a Diachronic Perspective
    On rare typological features of the Zamucoan languages, in the framework of the Chaco linguistic area Pier Marco Bertinetto Luca Ciucci Scuola Normale Superiore di Pisa The Zamucoan family Ayoreo ca. 4500 speakers Old Zamuco (a.k.a. Ancient Zamuco) spoken in the XVIII century, extinct Chamacoco (Ɨbɨtoso, Tomarâho) ca. 1800 speakers The Zamucoan family The first stable contact with Zamucoan populations took place in the early 18th century in the reduction of San Ignacio de Samuco. The Jesuit Ignace Chomé wrote a grammar of Old Zamuco (Arte de la lengua zamuca). The Chamacoco established friendly relationships by the end of the 19th century. The Ayoreos surrended rather late (towards the middle of the last century); there are still a few nomadic small bands in Northern Paraguay. The Zamucoan family Main typological features -Fusional structure -Word order features: - SVO - Genitive+Noun - Noun + Adjective Zamucoan typologically rare features Nominal tripartition Radical tenselessness Nominal aspect Affix order in Chamacoco 3 plural Gender + classifiers 1 person ø-marking in Ayoreo realis Traces of conjunct / disjunct system in Old Zamuco Greater plural and clusivity Para-hypotaxis Nominal tripartition Radical tenselessness Nominal aspect Affix order in Chamacoco 3 plural Gender + classifiers 1 person ø-marking in Ayoreo realis Traces of conjunct / disjunct system in Old Zamuco Greater plural and clusivity Para-hypotaxis Nominal tripartition All Zamucoan languages present a morphological tripartition in their nominals. The base-form (BF) is typically used for predication. The singular-BF is (Ayoreo & Old Zamuco) or used to be (Cham.) the basis for any morphological operation. The full-form (FF) occurs in argumental position.
    [Show full text]
  • The Renewal of Intensifiers and Variations in Language Registers: a Case-Study of Very, Really, So and Totally Lucile Bordet
    The renewal of intensifiers and variations in language registers: a case-study of very, really, so and totally Lucile Bordet To cite this version: Lucile Bordet. The renewal of intensifiers and variations in language registers: a case-study ofvery, really, so and totally. Intensity, intensification and intensifying modification across languages, Nov 2015, Vercelli, Italy. hal-01874168 HAL Id: hal-01874168 https://hal.archives-ouvertes.fr/hal-01874168 Submitted on 16 Feb 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The renewal of intensifiers and variations in language registers: a case- study of very, really, so and totally Lucile Bordet Université Jean Moulin - Lyon 3 CEL EA 1663 Abstract: This paper investigates the renewal of intensifiers in English. Intensifiers are popularised because of their intensifying potential but through frequency of use they lose their force. That is when the renewal process occurs and promotes new adverbs to the rank of intensifiers. This has consequences on language register. “Older” intensifiers are not entirely replaced by fresher intensifiers. They remain in use, but are assigned new functions in different contexts. My assumption is that intensifiers that have recently emerged tend to bear on parts of speech belonging to colloquial language, while older intensifiers modify parts of speech belonging mostly to the standard or formal registers.
    [Show full text]
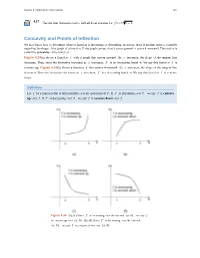
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]