Model Comparison: Deviance-Based Approaches
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Fast Computation of the Deviance Information Criterion for Latent Variable Models
Crawford School of Public Policy CAMA Centre for Applied Macroeconomic Analysis Fast Computation of the Deviance Information Criterion for Latent Variable Models CAMA Working Paper 9/2014 January 2014 Joshua C.C. Chan Research School of Economics, ANU and Centre for Applied Macroeconomic Analysis Angelia L. Grant Centre for Applied Macroeconomic Analysis Abstract The deviance information criterion (DIC) has been widely used for Bayesian model comparison. However, recent studies have cautioned against the use of the DIC for comparing latent variable models. In particular, the DIC calculated using the conditional likelihood (obtained by conditioning on the latent variables) is found to be inappropriate, whereas the DIC computed using the integrated likelihood (obtained by integrating out the latent variables) seems to perform well. In view of this, we propose fast algorithms for computing the DIC based on the integrated likelihood for a variety of high- dimensional latent variable models. Through three empirical applications we show that the DICs based on the integrated likelihoods have much smaller numerical standard errors compared to the DICs based on the conditional likelihoods. THE AUSTRALIAN NATIONAL UNIVERSITY Keywords Bayesian model comparison, state space, factor model, vector autoregression, semiparametric JEL Classification C11, C15, C32, C52 Address for correspondence: (E) [email protected] The Centre for Applied Macroeconomic Analysis in the Crawford School of Public Policy has been established to build strong links between professional macroeconomists. It provides a forum for quality macroeconomic research and discussion of policy issues between academia, government and the private sector. The Crawford School of Public Policy is the Australian National University’s public policy school, serving and influencing Australia, Asia and the Pacific through advanced policy research, graduate and executive education, and policy impact. -

A Generalized Linear Model for Binomial Response Data
A Generalized Linear Model for Binomial Response Data Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 1 / 46 Now suppose that instead of a Bernoulli response, we have a binomial response for each unit in an experiment or an observational study. As an example, consider the trout data set discussed on page 669 of The Statistical Sleuth, 3rd edition, by Ramsey and Schafer. Five doses of toxic substance were assigned to a total of 20 fish tanks using a completely randomized design with four tanks per dose. Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 2 / 46 For each tank, the total number of fish and the number of fish that developed liver tumors were recorded. d=read.delim("http://dnett.github.io/S510/Trout.txt") d dose tumor total 1 0.010 9 87 2 0.010 5 86 3 0.010 2 89 4 0.010 9 85 5 0.025 30 86 6 0.025 41 86 7 0.025 27 86 8 0.025 34 88 9 0.050 54 89 10 0.050 53 86 11 0.050 64 90 12 0.050 55 88 13 0.100 71 88 14 0.100 73 89 15 0.100 65 88 16 0.100 72 90 17 0.250 66 86 18 0.250 75 82 19 0.250 72 81 20 0.250 73 89 Copyright c 2017 Dan Nettleton (Iowa State University) Statistics 510 3 / 46 One way to analyze this dataset would be to convert the binomial counts and totals into Bernoulli responses. -

Comparison of Some Chemometric Tools for Metabonomics Biomarker Identification ⁎ Réjane Rousseau A, , Bernadette Govaerts A, Michel Verleysen A,B, Bruno Boulanger C
Available online at www.sciencedirect.com Chemometrics and Intelligent Laboratory Systems 91 (2008) 54–66 www.elsevier.com/locate/chemolab Comparison of some chemometric tools for metabonomics biomarker identification ⁎ Réjane Rousseau a, , Bernadette Govaerts a, Michel Verleysen a,b, Bruno Boulanger c a Université Catholique de Louvain, Institut de Statistique, Voie du Roman Pays 20, B-1348 Louvain-la-Neuve, Belgium b Université Catholique de Louvain, Machine Learning Group - DICE, Belgium c Eli Lilly, European Early Phase Statistics, Belgium Received 29 December 2006; received in revised form 15 June 2007; accepted 22 June 2007 Available online 29 June 2007 Abstract NMR-based metabonomics discovery approaches require statistical methods to extract, from large and complex spectral databases, biomarkers or biologically significant variables that best represent defined biological conditions. This paper explores the respective effectiveness of six multivariate methods: multiple hypotheses testing, supervised extensions of principal (PCA) and independent components analysis (ICA), discriminant partial least squares, linear logistic regression and classification trees. Each method has been adapted in order to provide a biomarker score for each zone of the spectrum. These scores aim at giving to the biologist indications on which metabolites of the analyzed biofluid are potentially affected by a stressor factor of interest (e.g. toxicity of a drug, presence of a given disease or therapeutic effect of a drug). The applications of the six methods to samples of 60 and 200 spectra issued from a semi-artificial database allowed to evaluate their respective properties. In particular, their sensitivities and false discovery rates (FDR) are illustrated through receiver operating characteristics curves (ROC) and the resulting identifications are used to show their specificities and relative advantages.The paper recommends to discard two methods for biomarker identification: the PCA showing a general low efficiency and the CART which is very sensitive to noise. -
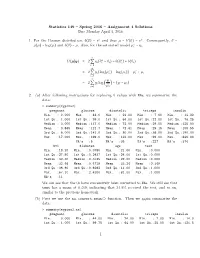
Statistics 149 – Spring 2016 – Assignment 4 Solutions Due Monday April 4, 2016 1. for the Poisson Distribution, B(Θ) =
Statistics 149 { Spring 2016 { Assignment 4 Solutions Due Monday April 4, 2016 1. For the Poisson distribution, b(θ) = eθ and thus µ = b′(θ) = eθ. Consequently, θ = ∗ g(µ) = log(µ) and b(θ) = µ. Also, for the saturated model µi = yi. n ∗ ∗ D(µSy) = 2 Q yi(θi − θi) − b(θi ) + b(θi) i=1 n ∗ ∗ = 2 Q yi(log(µi ) − log(µi)) − µi + µi i=1 n yi = 2 Q yi log − (yi − µi) i=1 µi 2. (a) After following instructions for replacing 0 values with NAs, we summarize the data: > summary(mypima2) pregnant glucose diastolic triceps insulin Min. : 0.000 Min. : 44.0 Min. : 24.00 Min. : 7.00 Min. : 14.00 1st Qu.: 1.000 1st Qu.: 99.0 1st Qu.: 64.00 1st Qu.:22.00 1st Qu.: 76.25 Median : 3.000 Median :117.0 Median : 72.00 Median :29.00 Median :125.00 Mean : 3.845 Mean :121.7 Mean : 72.41 Mean :29.15 Mean :155.55 3rd Qu.: 6.000 3rd Qu.:141.0 3rd Qu.: 80.00 3rd Qu.:36.00 3rd Qu.:190.00 Max. :17.000 Max. :199.0 Max. :122.00 Max. :99.00 Max. :846.00 NA's :5 NA's :35 NA's :227 NA's :374 bmi diabetes age test Min. :18.20 Min. :0.0780 Min. :21.00 Min. :0.000 1st Qu.:27.50 1st Qu.:0.2437 1st Qu.:24.00 1st Qu.:0.000 Median :32.30 Median :0.3725 Median :29.00 Median :0.000 Mean :32.46 Mean :0.4719 Mean :33.24 Mean :0.349 3rd Qu.:36.60 3rd Qu.:0.6262 3rd Qu.:41.00 3rd Qu.:1.000 Max. -

Bayesian Methods: Review of Generalized Linear Models
Bayesian Methods: Review of Generalized Linear Models RYAN BAKKER University of Georgia ICPSR Day 2 Bayesian Methods: GLM [1] Likelihood and Maximum Likelihood Principles Likelihood theory is an important part of Bayesian inference: it is how the data enter the model. • The basis is Fisher’s principle: what value of the unknown parameter is “most likely” to have • generated the observed data. Example: flip a coin 10 times, get 5 heads. MLE for p is 0.5. • This is easily the most common and well-understood general estimation process. • Bayesian Methods: GLM [2] Starting details: • – Y is a n k design or observation matrix, θ is a k 1 unknown coefficient vector to be esti- × × mated, we want p(θ Y) (joint sampling distribution or posterior) from p(Y θ) (joint probabil- | | ity function). – Define the likelihood function: n L(θ Y) = p(Y θ) | i| i=1 Y which is no longer on the probability metric. – Our goal is the maximum likelihood value of θ: θˆ : L(θˆ Y) L(θ Y) θ Θ | ≥ | ∀ ∈ where Θ is the class of admissable values for θ. Bayesian Methods: GLM [3] Likelihood and Maximum Likelihood Principles (cont.) Its actually easier to work with the natural log of the likelihood function: • `(θ Y) = log L(θ Y) | | We also find it useful to work with the score function, the first derivative of the log likelihood func- • tion with respect to the parameters of interest: ∂ `˙(θ Y) = `(θ Y) | ∂θ | Setting `˙(θ Y) equal to zero and solving gives the MLE: θˆ, the “most likely” value of θ from the • | parameter space Θ treating the observed data as given. -

What I Should Have Described in Class Today
Statistics 849 Clarification 2010-11-03 (p. 1) What I should have described in class today Sorry for botching the description of the deviance calculation in a generalized linear model and how it relates to the function dev.resids in a glm family object in R. Once again Chen Zuo pointed out the part that I had missed. We need to use positive contributions to the deviance for each observation if we are later to take the square roots of these quantities. To ensure that these are all positive we establish a baseline level for the deviance, which is the lowest possible value of the deviance, corresponding to a saturated model in which each observation has one parameter associated with it. Another value quoted in the summary output is the null deviance, which is the deviance for the simplest possible model (the \null model") corresponding to a formula like > data(Contraception, package = "mlmRev") > summary(cm0 <- glm(use ~ 1, binomial, Contraception)) Call: glm(formula = use ~ 1, family = binomial, data = Contraception) Deviance Residuals: Min 1Q Median 3Q Max -0.9983 -0.9983 -0.9983 1.3677 1.3677 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -0.43702 0.04657 -9.385 <2e-16 (Dispersion parameter for binomial family taken to be 1) Null deviance: 2590.9 on 1933 degrees of freedom Residual deviance: 2590.9 on 1933 degrees of freedom AIC: 2592.9 Number of Fisher Scoring iterations: 4 Notice that the coefficient estimate, -0.437022, is the logit transformation of the proportion of positive responses > str(y <- as.integer(Contraception[["use"]]) - 1L) int [1:1934] 0 0 0 0 0 0 0 0 0 0 .. -

The Deviance Information Criterion: 12 Years On
J. R. Statist. Soc. B (2014) The deviance information criterion: 12 years on David J. Spiegelhalter, University of Cambridge, UK Nicola G. Best, Imperial College School of Public Health, London, UK Bradley P. Carlin University of Minnesota, Minneapolis, USA and Angelika van der Linde Bremen, Germany [Presented to The Royal Statistical Society at its annual conference in a session organized by the Research Section on Tuesday, September 3rd, 2013, Professor G. A.Young in the Chair ] Summary.The essentials of our paper of 2002 are briefly summarized and compared with other criteria for model comparison. After some comments on the paper’s reception and influence, we consider criticisms and proposals for improvement made by us and others. Keywords: Bayesian; Model comparison; Prediction 1. Some background to model comparison Suppose that we have a given set of candidate models, and we would like a criterion to assess which is ‘better’ in a defined sense. Assume that a model for observed data y postulates a density p.y|θ/ (which may include covariates etc.), and call D.θ/ =−2log{p.y|θ/} the deviance, here considered as a function of θ. Classical model choice uses hypothesis testing for comparing nested models, e.g. the deviance (likelihood ratio) test in generalized linear models. For non- nested models, alternatives include the Akaike information criterion AIC =−2log{p.y|θˆ/} + 2k where θˆ is the maximum likelihood estimate and k is the number of parameters in the model (dimension of Θ). AIC is built with the aim of favouring models that are likely to make good predictions. -

Heteroscedastic Errors
Heteroscedastic Errors ◮ Sometimes plots and/or tests show that the error variances 2 σi = Var(ǫi ) depend on i ◮ Several standard approaches to fixing the problem, depending on the nature of the dependence. ◮ Weighted Least Squares. ◮ Transformation of the response. ◮ Generalized Linear Models. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Weighted Least Squares ◮ Suppose variances are known except for a constant factor. 2 2 ◮ That is, σi = σ /wi . ◮ Use weighted least squares. (See Chapter 10 in the text.) ◮ This usually arises realistically in the following situations: ◮ Yi is an average of ni measurements where you know ni . Then wi = ni . 2 ◮ Plots suggest that σi might be proportional to some power of 2 γ γ some covariate: σi = kxi . Then wi = xi− . Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Variances depending on (mean of) Y ◮ Two standard approaches are available: ◮ Older approach is transformation. ◮ Newer approach is use of generalized linear model; see STAT 402. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Transformation ◮ Compute Yi∗ = g(Yi ) for some function g like logarithm or square root. ◮ Then regress Yi∗ on the covariates. ◮ This approach sometimes works for skewed response variables like income; ◮ after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. ◮ See page 130ff and check under transformations and Box-Cox in the index. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Generalized Linear Models ◮ Transformation uses the model T E(g(Yi )) = xi β while generalized linear models use T g(E(Yi )) = xi β ◮ Generally latter approach offers more flexibility. -

And the Winner Is…? How to Pick a Better Model Part 2 – Goodness-Of-Fit and Internal Stability
And The Winner Is…? How to Pick a Better Model Part 2 – Goodness-of-Fit and Internal Stability Dan Tevet, FCAS, MAAA Goodness-of-Fit • Trying to answer question: How well does our model fit the data? • Can be measured on training data or on holdout data • By identifying areas of poor model fit, we may be able to improve our model • A few ways to measure goodness-of-fit – Squared or absolute error – Likelihood/log-likelihood – AIC/BIC – Deviance/deviance residuals – Plot of actual versus predicted target Liberty Mutual Insurance Squared Error & Absolute Error • For each record, calculate the squared or absolute difference between actual and predicted target variable • Easy and intuitive, but generally inappropriate for insurance data, and can lead to selection of wrong model • Squared error appropriate for Normal data, but insurance data generally not Normal Liberty Mutual Insurance Residuals • Raw residual = yi – μi, where y is actual value of target variable and μ is predicted value • In simple linear regression, residuals are supposed to be Normally distributed, and departure from Normality indicates poor fit • For insurance data, raw residuals are highly skewed and generally not useful Liberty Mutual Insurance Likelihood • The probability, as predicted by our model, that what actually did occur would occur • A GLM calculates the parameters that maximize likelihood • Higher likelihood better model fit (very simple terms) • Problem with likelihood – adding a variable always improves likelihood Liberty Mutual Insurance AIC & BIC – penalized -

Robustbase: Basic Robust Statistics
Package ‘robustbase’ June 2, 2021 Version 0.93-8 VersionNote Released 0.93-7 on 2021-01-04 to CRAN Date 2021-06-01 Title Basic Robust Statistics URL http://robustbase.r-forge.r-project.org/ Description ``Essential'' Robust Statistics. Tools allowing to analyze data with robust methods. This includes regression methodology including model selections and multivariate statistics where we strive to cover the book ``Robust Statistics, Theory and Methods'' by 'Maronna, Martin and Yohai'; Wiley 2006. Depends R (>= 3.5.0) Imports stats, graphics, utils, methods, DEoptimR Suggests grid, MASS, lattice, boot, cluster, Matrix, robust, fit.models, MPV, xtable, ggplot2, GGally, RColorBrewer, reshape2, sfsmisc, catdata, doParallel, foreach, skewt SuggestsNote mostly only because of vignette graphics and simulation Enhances robustX, rrcov, matrixStats, quantreg, Hmisc EnhancesNote linked to in man/*.Rd LazyData yes NeedsCompilation yes License GPL (>= 2) Author Martin Maechler [aut, cre] (<https://orcid.org/0000-0002-8685-9910>), Peter Rousseeuw [ctb] (Qn and Sn), Christophe Croux [ctb] (Qn and Sn), Valentin Todorov [aut] (most robust Cov), Andreas Ruckstuhl [aut] (nlrob, anova, glmrob), Matias Salibian-Barrera [aut] (lmrob orig.), Tobias Verbeke [ctb, fnd] (mc, adjbox), Manuel Koller [aut] (mc, lmrob, psi-func.), Eduardo L. T. Conceicao [aut] (MM-, tau-, CM-, and MTL- nlrob), Maria Anna di Palma [ctb] (initial version of Comedian) 1 2 R topics documented: Maintainer Martin Maechler <[email protected]> Repository CRAN Date/Publication 2021-06-02 10:20:02 UTC R topics documented: adjbox . .4 adjboxStats . .7 adjOutlyingness . .9 aircraft . 12 airmay . 13 alcohol . 14 ambientNOxCH . 15 Animals2 . 18 anova.glmrob . 19 anova.lmrob . -

Robust Fitting of Parametric Models Based on M-Estimation
Robust Fitting of Parametric Models Based on M-Estimation Andreas Ruckstuhl ∗ IDP Institute of Data Analysis and Process Design ZHAW Zurich University of Applied Sciences in Winterthur Version 2018† ∗Email Address: [email protected]; Internet: http://www.idp.zhaw.ch †The author thanks Amanda Strong for their help in translating the original German version into English. Contents 1. Basic Concepts 1 1.1. The Regression Model and the Outlier Problem . ..... 1 1.2. MeasuringRobustness . 3 1.3. M-Estimation................................. 7 1.4. InferencewithM-Estimators . 10 2. Linear Regression 12 2.1. RegressionM-Estimation . 12 2.2. Example from Molecular Spectroscopy . 13 2.3. General Regression M-Estimation . 17 2.4. Robust Regression MM-Estimation . 19 2.5. Robust Inference and Variable Selection . ...... 23 3. Generalized Linear Models 29 3.1. UnifiedModelFormulation . 29 3.2. RobustEstimatingProcedure . 30 4. Multivariate Analysis 34 4.1. Robust Estimation of the Covariance Matrix . ..... 34 4.2. PrincipalComponentAnalysis . 39 4.3. Linear Discriminant Analysis . 42 5. Baseline Removal Using Robust Local Regression 45 5.1. AMotivatingExample.. .. .. .. .. .. .. .. 45 5.2. LocalRegression ............................... 45 5.3. BaselineRemoval............................... 49 6. Some Closing Comments 51 6.1. General .................................... 51 6.2. StatisticsPrograms. 51 6.3. Literature ................................... 52 A. Appendix 53 A.1. Some Thoughts on the Location Model . 53 A.2. Calculation of Regression M-Estimations . ....... 54 A.3. More Regression Estimators with High Breakdown Points ........ 56 Bibliography 58 Objectives The block course Robust Statistics in the post-graduated course (Weiterbildungslehrgang WBL) in applied statistics at the ETH Zürich should 1. introduce problems where robust procedures are advantageous, 2. explain the basic idea of robust methods for linear models, and 3. -

Tree Species Richness Predicted Using a Spatial Environmental Model Including Forest Area and Frost Frequency, Eastern USA
RESEARCH ARTICLE Tree species richness predicted using a spatial environmental model including forest area and frost frequency, eastern USA 1 2 3 Youngsang KwonID *, Chris P. S. Larsen , Monghyeon Lee 1 Department of Earth Sciences, University of Memphis, Memphis, Tennessee, United States of America, 2 Department of Geography, University at Buffalo, Buffalo, New York, United States of America, 3 Geospatial Information Sciences, University of Texas at Dallas, Richardson, Texas, United States of America a1111111111 a1111111111 * [email protected] a1111111111 a1111111111 a1111111111 Abstract Assessing geographic patterns of species richness is essential to develop biological conser- vation as well as to understand the processes that shape these patterns. We aim to improve OPEN ACCESS geographic prediction of tree species richness (TSR) across eastern USA by using: 1) Citation: Kwon Y, Larsen CPS, Lee M (2018) Tree gridded point-sample data rather than spatially generalized range maps for the TSR out- species richness predicted using a spatial come variable, 2) new predictor variables (forest area FA; mean frost day frequency MFDF) environmental model including forest area and and 3) regression models that account for spatial autocorrelation. TSR was estimated in 50 frost frequency, eastern USA. PLoS ONE 13(9): km by 50 km grids using Forest Inventory and Analysis (FIA) point-sample data. Eighteen e0203881. https://doi.org/10.1371/journal. pone.0203881 environmental predictor variables were employed, with the most effective set selected by a LASSO that reduced multicollinearity. Those predictors were then employed in Generalized Editor: Claudionor Ribeiro da Silva, Universidade Federal de Uberlandia, BRAZIL linear models (GLMs), and in Eigenvector spatial filtering (ESF) models that accounted for spatial autocorrelation.