DOCSLIB.ORG

Analysis of Sound.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Analysis of Sound.Pdf TABLE OF CONTENT 1.0 INTRODUCTION 1 The concept of sound 1 2.0 GENERAL PROPERTIES OF SOUND 3 2.1 frequency 3 2.2 Wavelength 4 2.3 Amplitude and intensity 5 2.4 Speed of sound in various media 6 3.0 DECIBEL LEVELS 7 4.0 SOUND QUALITY 8 5.0 BEHAVIOR OF SOUND WAVES 9 5.1 Reflection 9 5.2 Refraction 9 5.3 Diffraction 10 5.4 Echo 10 5.5 Reverberation 11 6.0 PRODUCTION OF SOUND WAVES 12 6.1 Musical instruments 12 6.2 Electronic amplification 12 6.3 The human voice 12 7.0 TYPES OF ORDINARY SOUND 13 7.1 Speech 13 7.2 Noise 13 7.3 Music 13 8.0 CONCLUSION 13 9.0 REFERENCES 13 Analysis of Sound ii 1.0 INTRODUCTION THE CONCEPT OF SOUND Sound is a disturbance of mechanical energy that propagates through matter as a longitudinal wave; it is a mechanical wave because it is characterized by these three attributes. First, there is a medium which carries the disturbance from one location to another. Typically, this medium is air; though it could be any material such as water or steel. The medium is simply a series of interconnected and interacting particles. Second, there is an original source of the wave, some vibrating object capable of disturbing the first particle of the medium. The vibrating object which creates the disturbance could be the vocal chords of a person, the vibrating string and sound board of a guitar or violin, the vibrating tines of a tuning fork, or the vibrating diaphragm of a radio speaker. Third, the sound wave is transported from one location to another by means of the particle interaction. If the sound wave is moving through air, then as one air particle is displaced from its equilibrium position, it exerts a push or pull on its nearest neighbors, causing them to be displaced from their equilibrium position. This particle interaction continues throughout the entire medium, with each particle interacting and causing a disturbance of its nearest neighbors. Humans perceive sound by the sense of hearing. By sound, we commonly mean the vibrations that travel through air and can be heard by humans. However, scientists and engineers use a wider definition of sound that includes low and high frequency vibrations in air that cannot be heard by humans, and vibrations that travel through all forms of matter, gases, liquids and solids. The scientific study of sound is called acoustics. Analysis of Sound 1 The result of such longitudinal vibrations is the creation of compressions and rarefactions within the air. Regardless of the source of the sound wave - whether it be a vibrating string or the vibrating tines of a tuning fork - sound is a longitudinal wave. And the essential characteristic of a longitudinal wave which distinguishes it from other types of waves is that the particles of the medium move in a direction parallel to the direction of energy transport. A propagating sound wave consists of alternating compressions and rarefactions which are detected by a receiver as changes in pressure. Structures in our ears, and also most man-made receptors, are sensitive to these changes in sound pressure (Richardson et al.1995, Gordon and Moscrop 1996). Since a sound wave consists of a repeating pattern of high pressure and low pressure regions moving through a medium, it is sometimes referred to as a pressure wave. Sound is characterized by the properties of sound waves, which are frequency, wavelength, period, amplitude, and speed. If a detector, whether it be the human ear or a man-made instrument is used to detect a sound wave, it would detect fluctuations in pressure as the sound wave impinges upon the detecting device. At one instant in time, the detector would detect a high pressure; this would correspond to the arrival of a compression at the detector site. At the next instant in time, the detector might detect normal pressure. And then finally a low pressure would be detected, corresponding to the arrival of a rarefaction at the detector site. Since the fluctuations in pressure as detected by the detector occur at periodic and regular time intervals, a plot of pressure vs. time would appear as a sine curve. The crests of the sine curve correspond to compressions; the troughs correspond to rarefactions; and the "zero point" corresponds to the pressure which the air would have if there were no disturbance moving through it (see figure 3) Analysis of Sound 2 2.0 GENERAL PROPERTIES OF SOUND Sound as a longitudinal wave is characterized by several features which are esoteric to longitudinal waves. Any simple sound, such as a musical note, may be completely described by specifying three perceptual characteristics: pitch, loudness (or intensity), and quality (or timbre). These characteristics correspond exactly to three physical characteristics: frequency, amplitude, and harmonic constitution, or waveform, respectively. 2.1 FREQUENCY. The frequency of a sound wave is the rate of oscillation or vibration of the wave particles (i.e. the rate amplitude cycles from high to low to high, etc.) The hertz (Hz) is a unit of frequency equaling one vibration or cycle per second (1 Hertz = 1 vibration/second). The Audible frequency range: the human ear is capable of detecting sound waves with a wide range of frequencies, ranging between approximately 20 Hz to 20 000 Hz. Any sound with a frequency below the audible range of hearing (i.e., less than 20 Hz) is known as an infrasound and any sound with a frequency above the audible range of hearing (i.e., more than 20 000 Hz) is known as an ultrasound. Such vibrations reach the inner ear when they are transmitted through air. The frequency of a wave refers to how often the particles of the medium vibrate when a wave passes through the medium. This frequency is measured as the number of complete back-and-forth vibrations of a particle of the medium per unit of time. If a particle of air undergoes 1000 longitudinal vibrations in 2 seconds, then the frequency of the wave would be 500 vibrations per second. As a sound wave moves through a medium, each particle of the medium vibrates at the same frequency. Subsequently, a guitar string vibrating at 500 Hz will set the air particles in the room vibrating at the same frequency of 500 Hz which carries a sound signal to the ear of a listener which is detected as a 500 Hz sound wave. Analysis of Sound 3 Sound Frequency and Pitch: The sensations of these frequencies are commonly referred to as the pitch of a sound. A high pitch sound corresponds to a high frequency and a low pitch sound corresponds to a low frequency. Amazingly, many people, especially those who have been musically trained, are capable of detecting a difference in frequency between two separate sounds which is as little as 2 Hz. When two sounds with a frequency difference of greater than 7 Hz are played simultaneously, most people are capable of detecting the presence of a complex wave pattern resulting from the interference and superposition of the two sound waves. Certain sound waves when played (and heard) simultaneously will produce a particularly pleasant sensation when heard, they are said to be consonant. 2.2 WAVELENGTH Wavelength (represented by the symbol λ, the Greek letter lambda) is the distance between a crest and the adjacent crest, or a trough and an adjacent trough, of a wave (see figure 4). A wave of very high frequency would produce a corresponding short wave length while a wave of low frequency would produce a large wavelength. Thus, a frequency of 20 Hz, at the bottom end of human audibility, has a very large wavelength: 56 ft (17 m). The top end frequency of 20,000 Hz is only 0.67 inches (17 mm). The wavelengths of sounds in the range of human audibility are comparable to the size of ordinary objects. To block out a sound wave, one needs something of much greater dimensions—width, height, and depth—than a mere cloth curtain. A thick concrete wall, for instance, may be enough to block out the Analysis of Sound 4 waves. Better still would be the use of materials that absorb sound, such as cork, or even the use of machines that produce sound waves which destructively interfere with the offending sound. 2.3 AMPLITUDE AND INTENSITY Amplitude is critical to the understanding of sound, though it is mathematically independent from the parameters so far discussed. Amplitude is defined as the maximum displacement of a vibrating material from its mean or rest position, amplitude is the "size" of a wave. The greater the amplitude, the greater the energy the wave contains: amplitude indicates intensity, commonly known as "volume," which is the rate at which a wave moves energy per unit of a cross-sectional area. The greater the amplitude of the wave, the harder the molecules strikes the eardrum and the louder the sound that is perceived. The amplitude of a sound wave can be expressed in terms of absolute units by measuring the actual distance of displacement of the air molecules, the changes in pressure as the wave passes, or the energy contained in the wave. Intensity of a sound wave is the amount of energy which is transported past a given area of the medium per unit of time. The greater the amplitude of vibrations of the particles of the medium, the greater the rate at which energy is transported through it, and the more intense that the sound wave is.
Load more

Recommended publications
  • The Science of String Instruments
    The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D.
    [Show full text]
  • Standing Waves and Sound
    Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go.
    [Show full text]
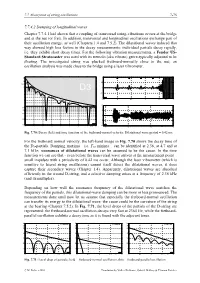
  • 7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
    7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples).
    [Show full text]
  • Giant Slinky: Quantitative Exhibit Activity
    Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position.
    [Show full text]
  • Woods for Wooden Musical Instruments S
    ISMA 2014, Le Mans, France Woods for Wooden Musical Instruments S. Yoshikawaa and C. Walthamb aKyushu University, Graduate School of Design, 4-9-1 Shiobaru, Minami-ku, 815-8540 Fukuoka, Japan bUniversity of British Columbia, Dept of Physics & Astronomy, 6224 Agricultural Road, Vancouver, BC, Canada V6T 1Z1 [email protected] 281 ISMA 2014, Le Mans, France In spite of recent advances in materials science, wood remains the preferred construction material for musical instruments worldwide. Some distinguishing features of woods (light weight, intermediate quality factor, etc.) are easily noticed if we compare material properties between woods, a plastic (acrylic), and a metal (aluminum). Woods common in musical instruments (strings, woodwinds, and percussions) are typically (with notable exceptions) softwoods (e.g. Sitka spruce) as tone woods for soundboards, hardwoods (e.g. amboyna) as frame woods for backboards, and monocots (e.g. bamboo) as bore woods for woodwind bodies. Moreover, if we consider the radiation characteristics of tap tones from sample plates of Sitka spruce, maple, and aluminum, a large difference is observed above around 2 kHz that is attributed to the relative strength of shear and bending deformations in flexural vibrations. This shear effect causes an appreciable increase in the loss factor at higher frequencies. The stronger shear effect in Sitka spruce than in maple and aluminum seems to be relevant to soundboards because its low-pass filter effect with a cutoff frequency of about 2 kHz tends to lend the radiated sound a desired softness. A classification diagram of traditional woods based on an anti-vibration parameter (density ρ/sound speed c) and transmission parameter cQ is proposed.
    [Show full text]
  • Chapter 5 Waves I: Generalities, Superposition & Standing Waves
    Chapter 5 Waves I: Generalities, Superposition & Standing Waves 5.1 The Important Stuff 5.1.1 Wave Motion Wave motion occurs when the mass elements of a medium such as a taut string or the surface of a liquid make relatively small oscillatory motions but collectively give a pattern which travels for long distances. This kind of motion also includes the phenomenon of sound, where the molecules in the air around us make small oscillations but collectively give a disturbance which can travel the length of a college classroom, all the way to the students dozing in the back. We can even view the up–and–down motion of inebriated spectators of sports events as wave motion, since their small individual motions give rise to a disturbance which travels around a stadium. The mathematics of wave motion also has application to electromagnetic waves (including visible light), though the physical origin of those traveling disturbances is quite different from the mechanical waves we study in this chapter; so we will hold off on studying electromagnetic waves until we study electricity and magnetism in the second semester of our physics course. Obviously, wave motion is of great importance in physics and engineering. 5.1.2 Types of Waves In some types of wave motion the motion of the elements of the medium is (for the most part) perpendicular to the motion of the traveling disturbance. This is true for waves on a string and for the people–wave which travels around a stadium. Such a wave is called a transverse wave. This type of wave is the easiest to visualize.
    [Show full text]
  • 1S-13 Slinky on Stand
    Sound light waves... waves... water waves... 1S-13 Slinky on Stand Creating longitudinal compression waves in a slinky What happens when you pull back and release one end of the slinky ? Physics 214 Fall 2010 11/18/2019 3 Moving one end of the Slinky back and forth created a local compression where the rings of the spring are closer together than in the rest of the Slinky. The slinky tries to return to equilibrium. But inertia cause the links to pass beyond. This create a compression. Then the links comes back to the equilibrium point due to the restoration force, i.e. the elastic force. The speed of the pulse may depend on factors such as tension in the Slinky and the mass of the Slinky. Energy is transferred through the Slinky as the pulse travels. The work done in moving one end of the Slinky increases both the potential energy of the spring and the kinetic energy of individual loops. This region of higher energy then moves along the Slinky and reaches the opposite end. There, the energy could be used to ring a bell or perform other types of work. Energy carried by water waves does substantial work over time in eroding and shaping a shoreline. If instead of moving your hand back and forth just once, you continue to produce pulses, you will send a series of longitudinal pulses down the Slinky. If equal time intervals separate the pulses, you produce a periodic wave. The time between pulses is the period T of the wave. The number of pulses or cycles per unit of time is the frequency f = 1/T.
    [Show full text]
  • Types of Waves Periodic Motion
    Lecture 19 Waves Types of waves Transverse waves Longitudinal waves Periodic Motion Superposition Standing waves Beats Waves Waves: •Transmit energy and information •Originate from: source oscillating Mechanical waves Require a medium for their transmission Involve mechanical displacement •Sound waves •Water waves (tsunami) •Earthquakes •Wave on a stretched string Non-mechanical waves Can propagate in a vacuum Electromagnetic waves Involve electric & magnetic fields •Light, • X-rays •Gamma waves, • radio waves •microwaves, etc Waves Mechanical waves •Need a source of disturbance •Medium •Mechanism with which adjacent sections of medium can influence each other Consider a stone dropped into water. Produces water waves which move away from the point of impact An object on the surface of the water nearby moves up and down and back and forth about its original position Object does not undergo any net displacement “Water wave” will move but the water itself will not be carried along. Mexican wave Waves Transverse and Longitudinal waves Transverse Waves Particles of the disturbed medium through which the wave passes move in a direction perpendicular to the direction of wave propagation Wave on a stretched string Electromagnetic waves •Light, • X-rays etc Longitudinal Waves Particles of the disturbed medium move back and forth in a direction along the direction of wave propagation. Mechanical waves •Sound waves Waves Transverse waves Pulse (wave) moves left to right Particles of rope move in a direction perpendicular to the direction of the wave Rope never moves in the direction of the wave Energy and not matter is transported by the wave Waves Transverse and Longitudinal waves Transverse Waves Motion of disturbed medium is in a direction perpendicular to the direction of wave propagation Longitudinal Waves Particles of the disturbed medium move in a direction along the direction of wave propagation.
    [Show full text]
  • Musical Acoustics Timbre / Tone Quality I
    Musical Acoustics Lecture 13 Timbre / Tone quality I Musical Acoustics, C. Bertulani 1 Waves: review distance x (m) At a given time t: y = A sin(2πx/λ) A time t (s) -A At a given position x: y = A sin(2πt/T) Musical Acoustics, C. Bertulani 2 Perfect Tuning Fork: Pure Tone • As the tuning fork vibrates, a succession of compressions and rarefactions spread out from the fork • A harmonic (sinusoidal) curve can be used to represent the longitudinal wave • Crests correspond to compressions and troughs to rarefactions • only one single harmonic (pure tone) is needed to describe the wave Musical Acoustics, C. Bertulani 3 Phase δ $ x ' % x ( y = Asin& 2π ) y = Asin' 2π + δ* % λ( & λ ) Musical Acoustics, C. Bertulani 4 € € Adding waves: Beats Superposition of 2 waves with slightly different frequency The amplitude changes as a function of time, so the intensity of sound changes as a function of time. The beat frequency (number of intensity maxima/minima per second): fbeat = |fa-fb| Musical Acoustics, C. Bertulani 5 The perceived frequency is the average of the two frequencies: f + f f = 1 2 perceived 2 The beat frequency (rate of the throbbing) is the difference€ of the two frequencies: fbeats = f1 − f 2 € Musical Acoustics, C. Bertulani 6 Factors Affecting Timbre 1. Amplitudes of harmonics 2. Transients (A sudden and brief fluctuation in a sound. The sound of a crack on a record, for example.) 3. Inharmonicities 4. Formants 5. Vibrato 6. Chorus Effect Two or more sounds are said to be in unison when they are at the same pitch, although often an OCTAVE may exist between them.
    [Show full text]
  • Physics 1240: Sound and Music
    Physics 1240: Sound and Music Today (7/15/19): Harmonics, Decibels Next time: Psychoacoustics: The Ear Review • Sound: a mechanical disturbance of the pressure in a medium that travels in the form of a longitudinal wave. • Simple harmonic motion: frequency increases when stiffness increases and increases when mass decreases • Sound propagation: reflection, absorption, refraction, diffraction • Doppler effect, sonic booms, factors affecting speed of sound (temperature, composition of medium, weather) • Overlapping sounds: 2-source interference, beats BA Clicker Question 5.1 If you are in a room with two speakers each producing sine waves with a wavelength of 2 meters, where should you stand if you don’t want to hear any sound? A) 2 meters from one speaker and 2 meters from the other B) 2 meters from one speaker and 4 meters from the other C) 2 meters from one speaker and 3 meters from the other D) 3 meters from one speaker and 5 meters from the other E) 1 meter from one speaker and 0.5 meters from the other BA Clicker Question 5.1 If you are in a room with two speakers each producing sine waves with a wavelength of 2 meters, where should you stand if you don’t want to hear any sound? A) 2 meters from one speaker and 2 meters from the other B) 2 meters from one speaker and 4 meters from the other C) 2 meters from one speaker and 3 meters from the other D) 3 meters from one speaker and 5 meters from the other E) 1 meter from one speaker and 0.5 meters from the other Review • Characteristics of Sound: What do we need to completely describe
    [Show full text]
  • PHYSICS the University of the State of New York REGENTS HIGH SCHOOL EXAMINATION
    PS/PHYSICS The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION PHYSICAL SETTING PHYSICS Tuesday, June 19, 2018 — 1:15 to 4:15 p.m., only The possession or use of any communications device is strictly prohibited when taking this examination. If you have or use any communications device, no matter how briefly, your examination will be invalidated and no score will be calculated for you. Answer all questions in all parts of this examination according to the directions provided in the examination booklet. A separate answer sheet for Part A and Part B–1 has been provided to you. Follow the instructions from the proctor for completing the student information on your answer sheet. Record your answers to the Part A and Part B–1 multiple-choice questions on this separate answer sheet. Record your answers for the questions in Part B–2 and Part C in your separate answer booklet. Be sure to fill in the heading on the front of your answer booklet. All answers in your answer booklet should be written in pen, except for graphs and drawings, which should be done in pencil. You may use scrap paper to work out the answers to the questions, but be sure to record all your answers on your separate answer sheet or in your answer booklet as directed. When you have completed the examination, you must sign the statement printed on your separate answer sheet, indicating that you had no unlawful knowledge of the questions or answers prior to the examination and that you have neither given nor received assistance in answering any of the questions during the examination.
    [Show full text]
  • Physics 2104C Study Guide 2005-06Opens in New Window
    Adult Basic Education Science Physics 2104C Waves, Light and Sound Study Guide Prerequisite: Physics 2104 A Credit Value:1 Text: Physics: Concepts and Connections. Nowikow et al. Irwin, 2002 Physics Concentration Physics 1104 Physics 2104A Physics 2104B Physics 2104C Physics 3104A Physics 3104B Physics 3104C Table of Contents To the Student ................................................................v Introduction to Physics 2104C..............................................v Use of Science Study Guides ...............................................v Recommended Evaluation ................................................ vi Unit 1 - Waves ........................................................... Page 1 Unit 2 - Light Properties I .................................................. Page 4 Unit 3 - Light Properties II ................................................. Page 7 Unit 4 - Sound Properties I ................................................. Page 9 Unit 5 - Sound Properties II ............................................... Page 13 Appendix A ............................................................ Page 17 Appendix B ............................................................ Page 25 To the Student I. Introduction to Physics 2104C This course will introduce you to the nature of sound and light. One way that light appears to behave is as a wave. (The other way light can behave is as a particle and you will study this in Physics 3104C). The study of light waves and then sound waves will involve many applications of both
    [Show full text]